Золотое сечение. Введение Глава Золотое сечение понятие и история исследования
 Скачать 425.01 Kb. Скачать 425.01 Kb.
|
ОглавлениеВведение…………………………………………………………………………..3 Глава 1. Золотое сечение: понятие и история исследования…………… 5 1.1. Понятие золотого сечения…………………………………………………...5 1.2.Математическая сущность золотого сечения……………………………….5 Глава 2. Методика исследования «золотого сечения»…………………..13 2.1. Золотое сечение в природе…………………………………………………13 2.2. Золотое сечение в архитектуре ……………………………………………16 2.3.Золотое сечение в строении человеческого тела ………………………….18 Заключение ……………………………………………………………………..25 Список использованной литературы и источников……………………….27 Введение"Аллах сотворил всему сущему должную меру..." (Сура "Ар Рад"). Есть вещи, которые нельзя объяснить. Вот вы подходите к пустой скамейке и садитесь на нее. Где вы сядете — посередине? Или, может быть, с самого края? Нет, скорее всего, не то и не другое. Вы сядете так, что отношение одной части скамейки к другой, относительно вашего тела, будет равно примерно 1,62. Простая вещь, абсолютно инстинктивная… Садясь на скамейку, вы произвели «золотое сечение». О золотом сечении знали еще в древнем Египте и Вавилоне, в Индии и Китае. Великий Пифагор создал тайную школу, где изучалась мистическая суть «золотого сечения». Евклид применил его, создавая свою геометрию, а Фидий — свои бессмертные скульптуры. Платон рассказывал, что Вселенная устроена согласно «золотому сечению». А Аристотель нашел соответствие «золотого сечения» этическому закону. Высшую гармонию «золотого сечения» будут проповедовать Леонардо да Винчи и Микеланджело, ведь красота и «золотое сечение» — это одно и то же. А христианские мистики будут рисовать на стенах своих монастырей пентаграммы «золотого сечения», спасаясь от Дьявола. При этом ученые — от Пачоли до Эйнштейна — будут искать, но так и не найдут его точного значения. Бесконечный ряд после запятой — 1,6180339887… Странная, загадочная, необъяснимая вещь: эта божественная пропорция мистическим образом сопутствует всему живому. Неживая природа не знает, что такое «золотое сечение». Но вы непременно увидите эту пропорцию и в изгибах морских раковин, и в форме цветов, и в облике жуков, и в красивом человеческом теле. Все живое и все красивое — все подчиняется божественному закону, имя которому — «золотое сечение». Так что же такое «золотое сечение»?… Что это за идеальное, божественное сочетание? Может быть, это закон красоты? Или все-таки он — мистическая тайна? Научный феномен или этический принцип? Ответ неизвестен до сих пор. Точнее — нет, известен. «Золотое сечение» — это и то, и другое, и третье. Только не по отдельности, а одновременно… И в этом его подлинная загадка, его великая тайна. Актуальность: Окружающий нас мир многообразен… Все, наверное, обращали внимание, что мы неодинаково относимся к предметам и явлениям окружающей действительности. Беспорядочность, бесформенность, несоразмерность воспринимаются нами как безобразное и производят отталкивающее впечатление. А предметы и явления, которым свойственна мера, целесообразность и гармония воспринимаются как красивое и вызывают у нас чувство восхищения, радости, поднимают настроение. Людей с давних времён волновал вопрос, подчиняются ли такие неуловимые вещи как красота и гармония, каким-либо математическим расчётам. Можно ли «проверить алгеброй гармонию?» – как сказал А.С. Пушкин. Цель работы – выявить «золотое сечение» в математике, природе, архитектуре, искусстве, технике. Задачи: - изучить понятия «пропорция»; «золотое сечение»; - исследовать присутствие золотого сечения в окружающей жизни; - изучить практическое применение этого понятия, провести эксперименты с элементами золотого сечения; - Научиться анализировать и делать выводы. Методы исследования: 1. Работа с учебной и научно-популярной литературой, ресурсами сети Интернет. 2. Социологический опрос. Эксперименты. 3. Наблюдение, сравнение, анализ, аналогия. Объект исследования: «золотое сечение». Предметы исследования: математика, искусство, живопись, природа. Глава 1.Золотое сечение: понятие и история исследования1.1. Понятие золотого сечения Золотое сечение – это пропорция, где меньшая часть относится к большей, как большая - ко всему целому. Приблизительная его величина 1,6180339887. В округленном процентном значении пропорции частей целого будут соотноситься как 62% на 38%. Это соотношение действует в формах пространства и времени. Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.). Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Французский архитектор Ле Корбюзье нашел, что в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют величинам золотого деления. Зодчий Хесира, изображенный на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого деления. Что же такое золотое сечение? 1.2.Математическая сущность золотого сечения Рассмотрим отрезок АВ.  А С В Его можно разделить точкой С на две части бесконечным множеством способов, но говорят что точка С производит золотое сечение отрезка АВ, если выполняется пропорция: длина меньшего отрезка так относится к длине большего, как больший отрезок относится к длине всего отрезка, т.е. 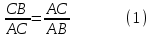 Термин золотое сечение ввёл в XVI веке великий художник, учёный и изобретатель Леонардо да Винчи. В истории утвердились три варианта названия: золотое сечение, золотая пропорция и третье – деление отрезка в среднем и крайнем отношениях. Кроме того, золотое сечение награждали эпитетами «божественное», «чудесное», «превосходнейшее», потому что-то, где оно присутствует, вызывает у нас ощущение красоты и гармонии. Чтобы и вы смогли увидеть золотое сечение в природе, в произведениях искусства, я научу вас сейчас делить отрезок в среднем и крайнем отношениях, т.е. делить отрезок в золотом отношении.  D D  E  B C A Дано : Отрезок АВ. Построить: золотое сечение отрезка АВ, то есть точку С так, чтобы 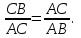 Построим прямоугольный треугольник, у которого один катет в два раза больше другого. Для этого восстановим в точке В перпендикуляр к прямой АВ и на нем отложим отрезок 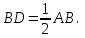 Далее, соединив точки A и D, отложим отрезок DE=BD, и, наконец, AC=AE. Точка С является искомой, она производит золотое сечение отрезка АВ. Далее, соединив точки A и D, отложим отрезок DE=BD, и, наконец, AC=AE. Точка С является искомой, она производит золотое сечение отрезка АВ.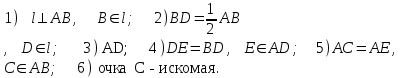 Доказательство. 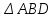 - прямоугольный по построению. По теореме Пифагора - прямоугольный по построению. По теореме Пифагора 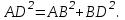 Так как отрезок AD равен сумме отрезков AE и ED, то равенство перепишем в виде: Так как отрезок AD равен сумме отрезков AE и ED, то равенство перепишем в виде: 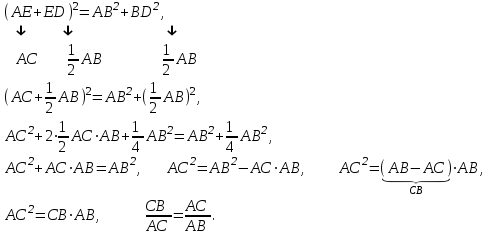 Задача имеет единственное решение. Деление отрезка в золотом отношении – это очень древняя задача. Она присутствует в «Началах» Евклида. Золотое сечение записывается с помощью пропорции. Пропорция – это равенство двух отношений. Всем, я думаю, интересно узнать численное значение этих отношений. Сейчас мы его найдем. Для удобства длину отрезка АВ обозначим за а , а длину отрезка АС – за х , то длина отрезка СВ будет а – х . А    х С а-х В х С а-х Ва Пропорция (1) примет вид : 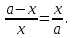 (2). (2).(Отношение длины меньшего отрезка а – х к длине большего отрезка х равно отношению большего отрезка х к длине всего отрезка а). Так как отношения составляющие пропорцию равны, то найдём численное значение, например, отношения 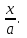 По свойству пропорции: произведение средних членов равно произведению крайних членов. Равенство (2) перепишется в виде  Раскроем скобки и все слагаемые перенесём в левую часть:  Решаю получившееся квадратное уравнение относительно х 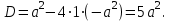  Так как, а – это длина отрезка, поэтому D > 0 , уравнение имеет 2 корня. 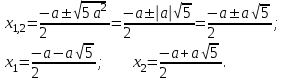 Напоминаю, что мы находим значение  Получилось два значения х, но х – это длина отрезка, т.е. число положительное. Проверим, удовлетворяет ли 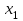 этому условию? ( этому условию? (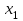 не удовлетворяет условию, так как меньше нуля). не удовлетворяет условию, так как меньше нуля). Удовлетворяет ли 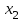 этому условию? этому условию? 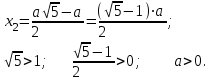 Значит, 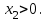 Находим отношение 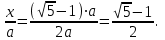 Вычисляю значение этого выражения с помощью микрокалькулятора с точностью до сотых. 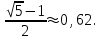 Следовательно, отношение длины меньшего отрезка к длине большего отрезка и отношение большего к длине всего отрезка равно 0,62 . Такое отношение и будет золотым. Полученное число обозначается буквой 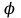 . Это первая буква в имени великого древнегреческого скульптора Фидия, жившего в V в до н.э., который часто использовал золотое отношение в своих произведениях. . Это первая буква в имени великого древнегреческого скульптора Фидия, жившего в V в до н.э., который часто использовал золотое отношение в своих произведениях. Итак, мы узнал, что такое золотое сечение и как разделить произвольный отрезок в золотом отношении. Так когда же некоторая точка С производит золотое сечение отрезка AD? (Точка С производит золотое сечение отрезка АВ, если выполняется пропорция: длина меньшего отрезка так относится к длине большего, как больший отрезок относится к длине всего отрезка, т.е. 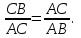 На уроках геометрии мы изучали равнобедренный треугольник, равносторонний треугольник, оказывается, существует ещё так называемый золотой треугольник.  Золотым называется такой равнобедренный треугольник, основание и боковая сторона которого находятся в золотом отношении: Золотым называется такой равнобедренный треугольник, основание и боковая сторона которого находятся в золотом отношении: В 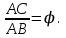 А С Прямоугольник, стороны которого находятся в золотом отношении, т.е. отношение ширины к длине даёт число 0,62, называется золотым прямоугольником.  L M L M K N В «золотом прямоугольнике» построим квадрат со стороной, равной меньшей стороне прямоугольника, у которого с прямоугольником общий прямой угол. Оказывается, снова получим золотой прямоугольник меньших размеров. В этом прямоугольнике снова построим квадрат, у которого с прямоугольником общий угол, и со стороной равной меньшей стороне прямоугольника. Снова получился золотой прямоугольник. Произведём несколько аналогичных построений. Видим, что весь прямоугольник оказался составленным из вращающихся квадратов. Соединим противолежащие вершины квадратов плавной кривой. Сделаем это с помощью циркуля следующим образом… 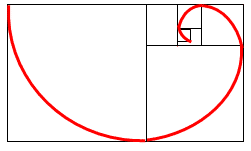 Мы получили кривую, которая является золотой спиралью. Для нахождения отрезков золотой пропорции восходящего и нисходящего рядов можно пользоваться пентаграммой. 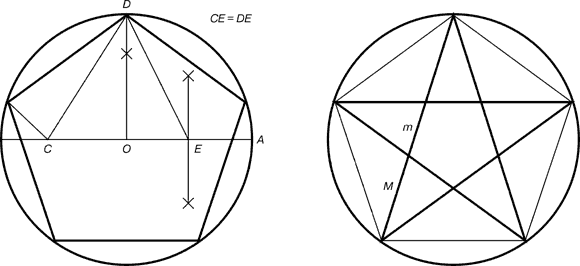 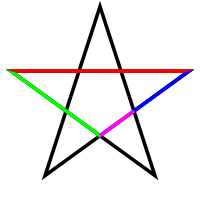 Для построения пентаграммы необходимо построить правильный пятиугольник. Способ его построения разработал немецкий живописец и график Альбрехт Дюрер (1471...1528). Пусть O – центр окружности, A – точка на окружности и Е – середина отрезка ОА. Перпендикуляр к радиусу ОА, восставленный в точке О, пересекается с окружностью в точке D. Пользуясь циркулем, отложим на диаметре отрезок CE = ED. Длина стороны вписанного в окружность правильного пятиугольника равна DC. Откладываем на окружности отрезки DC и получим пять точек для начертания правильного пятиугольника. Соединяем углы пятиугольника через один диагоналями и получаем пентаграмму. Все диагонали пятиугольника делят друг друга на отрезки, связанные между собой золотой пропорцией. Каждый конец пятиугольной звезды представляет собой золотой треугольник. Его стороны образуют угол 36° при вершине, а основание, отложенное на боковую сторону, делит ее в пропорции золотого сечения. П  роводим прямую АВ. От точки А откладываем на ней три раза отрезок О произвольной величины, через полученную точку Р проводим перпендикуляр к линии АВ, на перпендикуляре вправо и влево от точки Р откладываем отрезки О. Полученные точки d и d1 соединяем прямыми с точкой А. Отрезок dd1 откладываем на линию Ad1, получая точку С. Она разделила линию Ad1 в пропорции золотого сечения. Линиями Ad1 и dd1 пользуются для построения «золотого» прямоугольника. роводим прямую АВ. От точки А откладываем на ней три раза отрезок О произвольной величины, через полученную точку Р проводим перпендикуляр к линии АВ, на перпендикуляре вправо и влево от точки Р откладываем отрезки О. Полученные точки d и d1 соединяем прямыми с точкой А. Отрезок dd1 откладываем на линию Ad1, получая точку С. Она разделила линию Ad1 в пропорции золотого сечения. Линиями Ad1 и dd1 пользуются для построения «золотого» прямоугольника.Глава 2.Методика исследования «золотого сечения». Золотое сечение в природе В биологических исследованиях 1970-90 гг. показано, что, начиная с вирусов и растений, и кончая организмом человека, всюду выявляется “золотая пропорция”, характеризующая соразмерность и гармоничность их строения. “Золотое сечение” признано универсальным законом всех живых систем. Интерес человека к природе привёл к открытию её физических и математических закономерностей. Красота природных форм рождается во взаимодействии двух физических сил – тяготении и инерции. Золотая пропорция – это математический символ этого взаимодействия, поскольку выражает основные моменты живого роста: стремительный взлёт юных побегов сменяется замедленным ростом «по инерции» до момента цветения. Рассматривая расположение листьев на общем стебле многих растений, можно заметить, что между каждыми двумя парами листьев третья расположена в месте золотого сечения. Точка С делит отрезок АВ в золотом отношении, точка Е делит отрезок DA в золотом отношении и так далее.  Рассматривая расположение листьев на общем стебле растений: золотой ус, традесканция и алоэ, я выяснила, что между каждыми двумя из листьев третий расположен в определенном месте.  
Расчеты показали, что средний лист, располагается в месте “золотого сечения”. Золотую спираль также можно заметить в созданиях природы. Рассмотрим расположение семечек в корзине подсолнуха. Они выстраиваются вдоль спиралей, которые закручиваются как слева направо, так и справа налево. В одну сторону у среднего подсолнуха закручено 13 спиралей, в другую – 21 . Отношение 13/21 равно 0,62. У более крупных соцветий подсолнуха число соответствующих спиралей больше, но отношение числа спиралей, закручивающихся в разных направлениях также равно числу 0,62.  Похожее спиральное расположение наблюдается у чешуек сосновых шишек или ячеек ананаса.  По золотой спирали свёрнуты раковины многих улиток и моллюсков, некоторые пауки, сплетая паутину, закручивают нити вокруг центра по золотым спиралям. Рога архаров закручиваются по золотым спиралям.    Природа повторяет свои находки, как в малом, так и в большом. По золотым спиралям закручиваются многие галактики, в частности и галактика Солнечной системы.  Золотое сечение в архитектуре Математики и историки, архитекторы и философы с разных позиций то возносили, то низвергали закономерности согласования архитектурной формы. Особое внимание привлекало “золотое сечение”. Трудно найти человека, который бы не знал собора Василия Блаженного на Красной площади. Храм этот особенный; он отличается удивительным разнообразием форм и деталей, красочных покрытий; ему нет равных в нашей стране. Архитектурное убранство всего собора продиктовано определенной логикой и последовательностью развития форм. Исследователи пришли к выводу о преобладании в нем ряда “золотого сечения”. Примером использования золотого сечения в строительстве храмов может служить и Сретенский женский монастырь с. Батурино Прибайкальского района. Расчет размеров этой церкви, взятых из архива, позволил выявить, что композиционный замысел целиком связан с “золотым сечением”. На рисунке приведен композиционный замысел церкви, все расчеты; данные размеры приводятся в метрах. 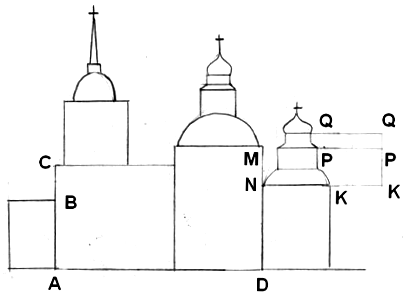 AC : AB = 11 : 6,8 = 1.62 DM : DN = 13 : 8 = 18 = 1,63 KQ : KP = 7 : 4.4 = 1,6 AB : CB = 6,8 : 4,2 = 1,62 DN : MN = 8 : 5 = 1,6 KP : PQ = 4,4 : 2,6 = 1,69 DN : NK = 8 : 4,6 = 1,7 длина / ширина = 26 : 16 = 1,63 Используя фотографию этого монастыря, произведя все интересующие нас измерения и вычисления, мы в очередной раз убедились, что “золотая пропорция”, действительно, использовалась при строительстве. Так как наше село и район не очень богаты архитектурными сооружениями, мы исследовали строения по фотографиям архитектур, и выяснили, что принцип “золотого сечения” на самом деле присутствует. Человек сам является творцом, создаёт замечательные произведения искусства, в которых просматривается золотая пропорция. Фидий руководил строительством храма Парфенон в Афинах.   Парфенон – это одно из красивейших произведений древнегреческой архитектуры. Он и сейчас, несмотря на то, что со времени его постройки прошло более 2,5 тысячелетий, производит огромное впечатление. Некогда белоснежный мрамор стал от времени золотисто-розовым. Величественное здание, стоящее на холме из известняка, возвышается над Афинами и их окрестностями. Но поражает оно не своими размерами, а гармоническим совершенством пропорций. Здание не вдавливается своей тяжестью в землю, а как бы парит над нею, кажется очень лёгким. Многие искусствоведы стремились раскрыть секрет того могучего эмоционального воздействия, которое это здание оказывает на зрителя. Разгадку они увидели в том, что в соотношениях многих частей храма присутствует золотая пропорция. Так, отношение высоты здания к его длине равно 0,62 . Отношения целого ряда частей Парфенона дают число 0,62. Говорят «… у греческого храма нет размеров, у него есть пропорции …». Надо сказать, что в эпоху Возрождения золотое сечение было очень популярно среди художников, скульпторов и архитекторов. Монах Лука Пачоли написал целую книгу «Божественная пропорция». Леонардо да Винчи, знающий о воздействии золотой пропорции на человека, выполнил к этой книге иллюстрации. Скульпторы, архитекторы, художники использовали и используют золотое сечение в своих произведениях, так как пропорции золотого сечения создают впечатление гармонии и красоты. Приобретенные мною знания о золотой пропорции еще больше убедили меня в том, что архитектура – это то, где золотое сечение является основополагающим принципом красоты, прочности, надежности, о чем говорят сами за себя произведения архитектуры и зодчества. Золотое сечение в строении человеческого тела В разные времена и у разных народов эталоны длины частей человека были одинаковыми: они происходили от человеческого тела. В человеке заложены пропорции, отобранные самой природой. Начало этим мерам дает рост человека. Деление тела точкой пупа – важнейший показатель “золотого сечения”. Художники, ученые, модельеры, дизайнеры делают свои расчеты, чертежи или наброски, исходя из соотношения “золотого сечения”. Они используют мерки с тела человека, сотворенного по этому принципу. Если эти пропорции совпадают с формулой “золотого сечения”, то внешность или тело человека считается идеально сложенными В строении черт лица человека и в руке, также есть множество примеров, приближающихся по значению к этой формуле. Я на практике решил проверить присутствие “золотого сечения” в частях человеческого тела – в росте, в кисти руки, в лицевой части головы. Для этого я провел необходимые измерения у своих одноклассников (11-12 лет), у молодых знакомых (18-20 лет) и у родителей одноклассников, у учителей (35-40 лет). Представляю по одному результату исследования из каждой возрастной группы. 1. Исследование роста. Измерения нескольких тысяч человеческих тел позволили обнаружить, что пупок делит высоту человека в золотом отношении. 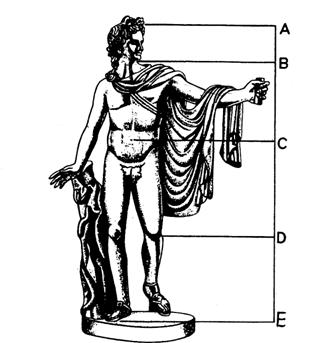 Основание шеи делит расстояние от макушки до пупка в золотом отношении. Эти пропорции я показал в изображении знаменитой скульптуры Аполлона Бельведерского. Аполлон считается образцом мужской красоты. Но не только создатель Аполлона, но и скульптор Фидий часто использовал золотую пропорцию в своих произведениях. Самыми знаменитыми из них были статуя Зевса Олимпийского,  которая считалась одним из семи чудес света, и статуя Афины Парфенос.  Были проведены исследования роста трех человек разных возрастных особенностей: Косоголова Юлия (11 лет) 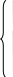 58 145 87 145 : 87 = 1,67 87 : 58 = 1,5 Немтина Юлия (19 лет) 62 162 100 162 : 100 = 1,62 100 : 62 = 1,61 Махмудова Масюда Муединовна (40 лет) 61 158 97 158 : 97 = 1,63 97 : 61 = 1,6 2. Исследование лицевой части головы. Оказывается, что у большинства людей, верхняя точка уха, на рисунке это точка В, делит высоту головы вместе с шеей, т.е. отрезок АС, в золотом отношении. Нижняя точка уха, точка D, делит в золотом отношении расстояние ВС, т.е. расстояние от верхней части уха до основания шеи. Подбородок делит расстояние от нижней точки уха до основания шеи в золотом отношении, т.е. точка Е делит в золотом отношении отрезок DC . 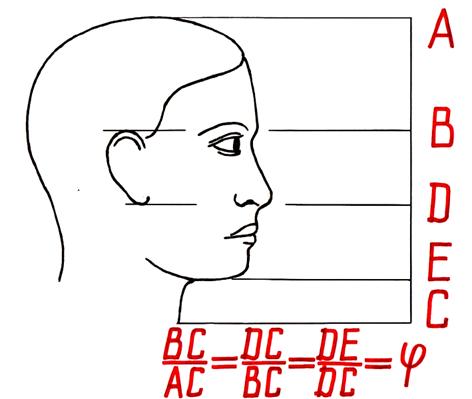 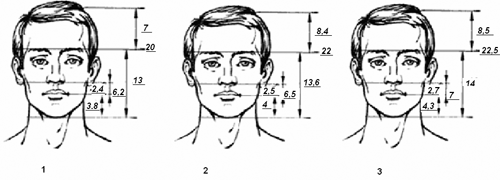 Проведенные исследования лиц трех человек разных возрастных особенностей: 1. Бочкарев Никита (12 лет) 3,8 : 2,4 = 1,58 6,2 : 3,8 = 1,63 20 : 13 = 1,53 13 : 7 = 1,85 2. Везняк Анастасия Вячеславовна (20 лет) 4 : 2,5 = 1,6 6,5 : 4 = 1,63 22 : 13,6 = 1,62 13,6 : 8,4 = 1,62 3 .Аблаева Ленара Серверовна (40 лет) 4,3 : 2,7 = 1,6 7 : 4,3 = 1,62 22,5 : 14 = 1,61 8,5 = 1,65 Исследование кисти руки.  Проведенные исследования кисти рук трех человек разных возрастных особенностей: Рябов Богдан (12 лет): a = 8 b = 4,5 b = 4,5 c = 3 a + b = 12,5 b + c = 7,5 12,5 : 8 = 1,56 7,5 : 4,5 = 1,67 8 : 4,5 = 1,78 4,5 : 3 = 1,5 Сейтмамутова Диана Диляверовна (27 лет) a = 9,2 b = 4,5 b = 4,5 c = 3,3 a + b = 13,7 b + c = 7,8 13,7 : 9,2 = 1,49 7,8 : 4,5 = 1,73 9,2 : 4,5 = 2 4,5 : 3,3 = 1,36 Мирвода Татьяна Федоровна (62 года) a = 9,5 b = 4,5 b = 4,5 c = 4 a + b = 14 b + c = 8,5 14 : 9,5 = 1,47 8,5 : 4,5 = 1,89 9,5 : 4,5 = 2,1 4,5 : 4 = 1,1 После всех вычислений я пришел квыводу, что “золотое сечение” присутствует в частях человеческого тела. Но чем старше человек, тем пропорция более приближена к “золотому сечению”, т.к. дети растут, организм их формируется, поэтому размеры тела изменяются. Из всего сказанного можно сделать выводы: Золотое сечение является отображением окружающегося мира Человеческое представление о красивом формировалось под влиянием порядка и гармонии Закономерности «Золотого сечения» заложены в подсознании человека, они использовались и используются архитекторами в своих работах. С возрастом увеличивается количество людей, выбирающих Золотую пропорцию. Золотое сечение имеет большое применение в нашей жизни. На летательных аппаратах с электромагнитными источниками энергии создаются прямоугольные ячейки с пропорцией золотого сечения. Заключение Принцип золотого сечения – высшее проявление структурного и функционального совершенства целого и его частей в искусстве, науке, технике и природе. Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему. Знакомство с принципами «золотого сечения», помогает видеть гармонию и целесообразность окружающих нас творений природы и человека. Можно сделать выводы: во-первых, золотое сечение – это один из основных основополагающих принципов природы; во-вторых, человеческое представление о красивом явно сформировалось под влиянием того, какой порядок и гармонию человек видит в природе. Несмотря на неприятие «золотого сечения» современными «официальными науками, оно повсеместно используется в технике, во многих странах мира, в том числе в России и Украине, довольно крупные учёные продолжают изучать и искать практическое применение одному из «золотых» математических принципов. Проведенные исследования доказали, что многое в окружающем мире подчиняется правилу золотого сечения. Человек различает окружающие его предметы по форме. Интерес к форме какого-либо предмета может быть продиктован жизненной необходимостью, а может быть вызван красотой формы. Форма, в основе построения которой лежат сочетание симметрии и золотого сечения, способствует наилучшему зрительному восприятию и появлению ощущения красоты и гармонии. Целое всегда состоит из частей, части разной величины находятся в определенном отношении друг к другу и к целому. Принцип золотого сечения – высшее проявление структурного и функционального совершенства целого и его частей в искусстве, науке, технике и природе. Значение золотого сечения в современной науке очень велико. Эта пропорция используется практически во всех областях знаний. Принципы «золотого сечения» используются в математике, физике, биологии, астрономии и др. науках, в архитектуре и др. искусствах. Они лежат в основе архитектурных пропорций многих замечательных произведений мирового зодчества, главным образом античности и Возрождения. Гениальный ученый Иоганн Кеплер поставил пропорцию «золотого сечения» на один уровень с самой знаменитой геометрической теоремой. Однако «золотому сечению» повезло меньше, чем теореме Пифагора – «классическая» наука и педагогика его игнорируют, а «официальная» математика не признаёт. Список использованной литературы и источниковАракелян Г. Б. Математика и история золотого сечения. - М.: Логос, 2016. Атанасян Л.С. Геометрия 7-9. — М.: «Просвещение», 2012. Азевич А.И. Двадцать уроков гармонии: гуманитарно-математический курс. – М., 2015. Бендукидзе А. Б. Золотое сечение: учебное пособие / А. Б. Бендукидзе; М, 1973. Васютинский Н. А. Золотая пропорция. - М.: Молодая гвардия, 2012. Волошинов А.В. Математика и искусство. М., 2016. Волошинов В.А. Пифагор. - М., 2010. Гика М. Эстетика пропорций в природе и искусстве: учебное пособие / М. Гика; М, 1936. Ковалев Ф.В. Золотое сечение в живописи – К: Высшая школа, 2015. Мурадова Р. Обобщающий урок по теме «Золотое сечение». // Математика (Приложение к газете «Первое сентября»). – 2014. № 1. Пидоу Д. Геометрия и искусство. – М.: Мир, 1989. Сабанеев Л. Л. Этюды Шопена в освещении закона золотого сечения. Опыт позитивного обоснования законов формы // Искусство. - 1925. -№ 2. Стахов А. Коды золотой пропорции. – М., 2014. Тимердинг Г. Е. Золотое сечение. -- Петербург, 1924. https://ru.wikipedia.org/wiki |
