металлические и деревянные конструкции. Кп МиДК(К). Введение и заключение писать конкретно по своему варианту!!!! Данные по заданию включать обязательно!

• Название: Введение и заключение писать конкретно по своему варианту!!!! Данные по заданию включать обязательно!
• Анкор: металлические и деревянные конструкции
• Дата: 14.04.2021
• Размер: 395.5 Kb.
• Имя файла: Кп МиДК(К).doc
• Тип: Документы; #194644

ВВЕДЕНИЕ И ЗАКЛЮЧЕНИЕ писать конкретно по своему варианту!!!!

Данные по заданию включать обязательно!

Выполнять ПЗ строго по нормоконтролю!

1 Расчет настила

Определяем толщину настила. При q = 27 кН/м², t_н = 10 мм. Определяем размеры настила по формуле (1.1):

l/t_н = ((4·n₀)/15)·(1+(72·E₁)/(n₀⁴·q)), (1.1)

l/t_н = ((4·150)/15)·(1+(72·2,26·10⁴) / (150⁴·2,7·10^-3)) = 87,5

Тогда:

l = t_н ·87,5 (1.2)

l = 1·93,5 = 87,5 см.

Определяем силу, растягивающую настил:

Н = n·(π²/4)·[f / l]²·E₁·t (1.3)

Н = 1,2·(π²/4)·[1/150]²·2,26·10⁴·1 = 2,97 кН/см.

Находим катет шва:

k_ш = Н/(β_ш·l_ш·R_уш^св·γ) (1.4)

k_ш = 2,97/(0,9·1·18·1) = 0,18 см.

Так как в строительных конструкциях нельзя применять сварные швы менее 4 мм, то мы принимаем k_ш = 4 мм.

2 Компоновка балочной клетки и расчет балок настила

Количество балок настила необходимо принять четным, т.к. при назначении балок настила необходимо учесть стык главной балки (на болтах). Поэтому принимаем 22 балок с шагом а = 85,7 см.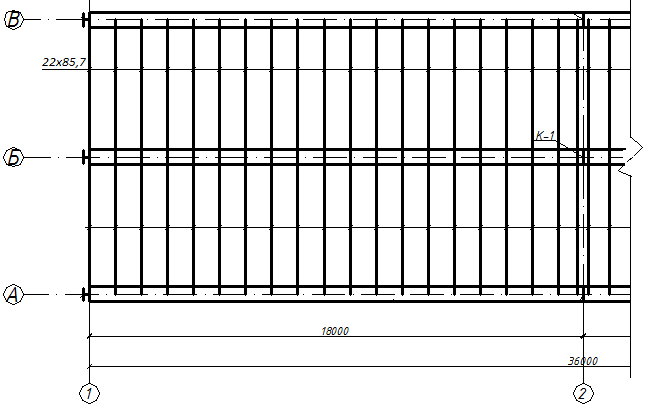

Рисунок 1 – Схема расположения балок настила

Производим сравнение двух вариантов.

Первый вариант

Определяем вес настила:
g = t_н·78,5 (2.1)
g = 1·78,5=78,5 кг/м² = 0,785 кН/м².
Нормативная нагрузка на балку настила будет равна:
q^н = (р^н + g^н) · а (2.2)
q^н = (27+0,785)·0,857 = 24 кН/м = 0, 24 кН/см.
Определим расчетную нагрузку на балку настила:
q^р = (n_рр^н+n_gg^н)·а (2.3)
q^р = (1,2·27+1,05·0,785)·0,857 = 28,47 кН/м.
Расчетный изгибающий момент, при длине балки настила равной 4м. равен:

М_max = (q·l²)/8 (2.4)
М_max = (28,47·4²)/8 = 56,94 кН·м = 5694 кН·см.
Требуемый момент сопротивления балки определяем по формуле:
W_нт.тр. = W_max / (C₁·R·γ) (2.5)
W_нт.тр. = 5694 / (1,1·22,5·1) = 230 см³.
Принимаем двутавр №22 по ГОСТ 8239-72, имеющий I = 2550 см⁴, W = 232 см³, вес g = 24 кг/м, ширину полки b = 11 см.

Проверяем только прогиб по формуле, т.к. W = 232 см³ > 230 см³.
f = (5/384)·q·l⁴ / (E·I) (2.6)
f =(5/384)·0,24·400⁴/(2,06·10⁴·2550) = 1,52 см < 1,6 см = (1/250)·l
Принятое сечение балки удовлетворяет условиям прочности и прогиба.

Определяем расход металла на 1 м² перекрытия:

настил : 78,5 кг/м²

балки настила : g/а = 24 / 0,875 = 28 кг/м².

Весь расход металла составит:
78,5 + 28 = 106,5 кг/м² = 1,065 кН/м².
Второй вариант

Принимаем длину балок настила l = 3,6 м, с шагом а = 0,8.

Определяем нормативную и расчетную нагрузки:
q^н = (р^н+g^н)·а (2.7)
q^н = (27+0,785)·0,8 = 22 кН/м = 0,22 кН/см.
q^р = (n_рр^н+n_gg^н)·а (2.8)
q^р = (1,2·27+1,05·0,785)·0,8 = 26,58 кН/м.
Расчетный изгибающий момент и требуемый момент сопротивления балки равен:

М_max=(q·l²)/8 (2.9)
М_max = (26,58·3,6²)/8 = 43,1 кН·м = 4310 кН·см.
W_нт.тр. = W_max / (C₁·R·γ) (2.10)
W_нт.тр. = 4310/(1,1·22,5·1) =174 см³.
Принимаем двутавр №20 по ГОСТ 8239-72, имеющий I=1840 см⁴, W = 184 см³, вес g = 21 кг/м.

Проверяем только прогиб по формуле, т.к. W = 184 см³ > W_тр = 174 см³.
f = (5/384)·q·l⁴/(E·I) (2.11)
f =(5/384)·0,22·360⁴/(2,06·10⁴·1840) =1,27 см < 1,44см = (1/250)·l
Принятое сечение балки удовлетворяет условиям прочности и прогиба. Нагрузку на вспомогательную балку от балок настила считаем равномерно распределенной. Определяем нормативную и расчетную нагрузку на нее:
q^н = (р^н + g^н + (g/а))·l (2.12)
q^н = [27+0,785+(0,21/0,8)]·3,6 = 101 кН/м = 1,01 кН/см.
q^р = [n_рр^н + n_g (g^н+(g/а)) ]·l (2.13)
q^р = [1,2·27+1,05·(0,785+(0,21/0,8))]·3,6 = 121 кН/м.
Определяем расчетный изгибающий момент и требуемый момент сопротивления балки:
М_max = (q·l²)/8 (2.14)
М_max = (121·4²)/8 = 242 кН·м = 24200 кН·см.
W_нт.тр. = W_max / (C₁·R·γ) (2.15)
W_нт.тр. = 24200/(1,1·22,5·1) = 978 см³.
Принимаем двутавр №45 имеющий I = 27696 см⁴, W = 1231 см³, ширину b = 16 см, толщину t = 1,42 мм, вес g = 66,5 кг/м. Исходя из того, что прочность удовлетворяет условию W = 1231см³>W_тр. = 978, проверяем балку на прогиб:
f = (5/384)·q·l⁴/(E·I) (2.16)
f =(5/384)·1,01·400⁴/(2,06·10⁴·27696) = 0,59 см < 1,6см =(1/250)·l
Весь расход металла по 2 варианту составит:
(78,5+(21/0,8)+(66,5/3,6)) = 123,22 кг/м².
Вывод: по расходу металла первый вариант оказался выгоднее.

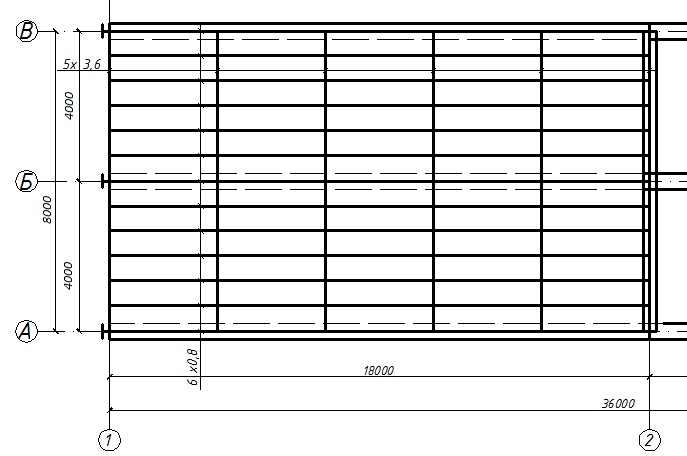
Рисунок 2 – Схема расположения балок

3 Подбор сечения балок
Требуется подобрать сечение сварной балки.

Определим нормативную и расчетную нагрузки на балку:
q^н = (р^н+g^н) (3.1)
q^н = 1,02·(27+1,065)·4= 114,5 кН/м = 1,14 кН/см.
q^р = (n_рр^н + n_gg^н)·а (3.2)
q^р = 1,02·(1,2·27+1,05·1,065)·4 = 136,8 кН/м.
Определяем расчетный изгибающий момент в середине пролета:
M_max = (ql²)/8 (3.3)
M_max = (136,8·18²)/8 = 5540,4 кН·м = 554040 кН·см.
Определим поперечную силу на опоре:
Q_max = (ql)/2 (3.4)
Q_max = (136,8·18)/2 = 1231,2 кН.
Главную балку рассчитываем с учетом развития пластических деформаций и определяем требуемый момент сопротивления балки, первоначально принимая с₁ = с = 1,1.
W_тр.= M_max/(c₁·R·) (3.5)
W_тр.= 554040/(1,1·23·1) = 21898,8 см³.
Определяем оптимальную высоту балки, предварительно задав ее высоту h = (1/10)l = 1,8 м и рассчитав толщину стенки t_ст = 7+(3·1800)/1000 = 12,4 мм, принимаем толщину стенки 12 мм.
h_опт = k·W/t_ст (3.6)
h_опт = 1,15·21898,8/1,2 = 155,4 см.
Минимальную высоту определяют по формуле:
h_min = ((5/24)·(c₁·R·l)/E)[l/f]((p^н+g^н)/(n_p·p^н+n_g·g^н)) (3.7)

h_min = ((5/24)·(1,1·23·1800·400)/2,06·10⁴)·((114,5)/(136,8)) = 154,2 см.
Строительную высоту балки определяем исходя из максимально возможной заданной высоты перекрытия и его конструкции:
h_стр^балки = h_стр^перекр – h_{балк.наст} – t_наст (3.8)
h_стр^балки = 320–22–1 = 297 см.
Сравнивая полученные высоты, принимаем высоту балки, близкую к оптимальной h = 160 см. Проверяем принятую толщину стенки:

По эмпирической формуле:
t_ст = 7+(3·h)/1000 (3.9)
t_ст = 7+(3·1600)/1000 = 11,8 мм.
Из условия работы стенки на касательные напряжения на опоре по формуле:
t_ст = (3/2)·(Q_max/(h·R_ср)) (3.10)
t_ст = (3/2)·(1231,2/(2·160·13,5)) = 0,86 см.
где R_ср =13,5кН/см²
Чтобы не применять продольных ребер жесткости:
t_ст = (hR/E)/5,5 (3.11)
t_ст = (16023/2,06·10⁴)/5,5 = 0,97 см.
Сравнивая полученную расчетным путем толщину стенки принятой (12 мм), приходим к выводу, что она удовлетворяет условию прочности на действие касательных напряжений и не требует укрепления ее продольным ребром жесткости для обеспечения местной устойчивости. Размеры горизонтальных поясных листов находим исходя из необходимой несущей способности балки. Для этого вычисляем требуемый момент инерции сечения балки:
I = (W·h)/2 (3.12)
I = (21898,8·160)/2 = 1751904 см⁴.
Находим момент инерции стенки балки, принимая толщину поясов 2см:
h_ст = h – 2t_п (3.13)
h_ст = 160–2·2 = 156 см.
I_ст = (t_ст·h_ст³)/12 (3.14)
I_ст = (1,2·156³)/12 = 379641,6 см⁴.
Момент инерции, приходящийся на поясные листы:

I_п = I – I_ст (3.15)
I_п = 1751904–379641,6 = 1372262,4 см⁴.
Момент инерции поясных листов балки относительно ее нейтральной оси I_п = 2А_п(h₀/2)², где А_п – площадь сечения пояса.

Моментом инерции поясов относительно их собственной оси ввиду его малости пренебрегаем.

Отсюда получаем требуемую площадь сечения поясов балки:
А_п = (2I_п)/h₀² (3.16)
А_п = (2·1372262,4)/158² = 110 см².
где h₀ = h – t_п = 160–2 =158 см.

Принимаем пояса из универсальной стали 550×20.

Проверяем принятую ширину (свес) пояса, исходя из их местной устойчивости:

b_св = b_п – 10 = 550 – 10 = 540 мм.
b_св./ t_п = 54/(2·2) = 13,5 см.
0,11·(h₀/ t_ст) = 0,11·(158/1,2) = 14,48 см.
0,5E/R = 14,96
13,5 < 14,48 < 14,96
Условие выполняется.

Проверяем несущую способность балки исходя из устойчивости стенки в области пластических деформаций балки в месте действия максимального момента, где Q и  = 0.
_ст = (h_ст/t_ст)R·E (3.17)
_ст = (156/1,2)23·2,06·10⁴ = 4,344
M  R··h₀²·t_ст·(A_п/А_ст+) (3.18)
где  = 0,24-0,15·(/R_ср)² – 8,5·10 ^-3·(_ст - 2,2)² = 0,24 - 0,04 = 0,2
М_max = 554040 < 23·1·158²·1,2·(110/156+0,2) = 562937 кН·см
Подобранное сечение балки проверяем на прочность. Для этого определяем момент инерции и момент сопротивления балки:
I = I_ст+I_п = I_ст + 2·b_п·t_п·(h_0п/2)² (3.19)
I = 379641,6 + 2·55·2·(158/2)² = 1752661,6 см⁴
W = I/(h/2) (3.20)
W = (1752661,6 ·2)/160 = 21908,27 см³
 = М_max/(С₁·W) (3.21)
 = 554040/(1,1·21908,27) = 23 кН/см².
 должна быть  R = 23кН/см², подобранное сечение балки удовлетворяет проверке и не имеет недонапряжения балки больше 5%. Проверку прогиба балки делать не нужно, так как принятая высота сечения больше минимума и регламентированный прогиб будет обеспечен.


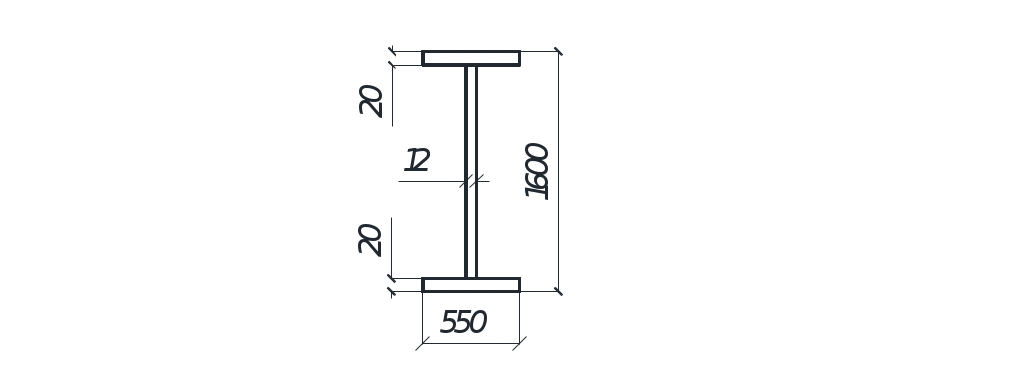
Рисунок 3 – Размеры сечения балки.

4 Изменение сечения сварной балки
х = l/6 = 18/6 = 3 м.
М₁ = [q·х·(l-x)]/2 (4.1)
М₁ = [121·3·(18-3)]/2 = 2723 кН·м = 272300 кН·см.
Q₁ = q·(l/2-x) (4.2)
Q₁ = 121·(18/2-3) = 726 кН.
Подбор измененного сечения ведем по упругой стадии работы материала по формуле:
W_{нт.треб.} = М_max/(R·) (4.3)
W₁ = 272300/(0,85·23) = 13928 см³
Определяем требуемый момент сопротивления и момент инерции измененного сечения, исходя из прочности сварного стыкового шва, работающего на растяжение:
I₁ = W₁·х(h/2) (4.4)
I₁ = 13928·(160/2) = 1114240 см⁴.
Определяем требуемый момент инерции поясов (I_ст = 397641,6 см⁴)
I_п1 = I₁ - I_ст = 1114240–397641,6 = 734598 см⁴.
Требуемая площадь сечения поясов
А_п1 = (2·I_п1)/h²₀₁ (4.5)
А_п1 = (2·734598)/158² = 58,85 см².
принимаем пояс 300×20 или, А_п1 = 60 см².

Принятый пояс удовлетворяет рекомендациям b_п1 = 20 см и b_п1>h/10 = 18 см. определяем момент инерции и момент сопротивления уменьшенного сечения:

I₁ = I_ст + 2·b₁·t_п·(h₀/2)² (4.6)
I₁ = 379641,6+2·30·2·(158/2)² = 1128562 см⁴
W₁ = (2·I₁)/h (4.7)
W₁ = (2·1128562)/160= 14107 см³
 = М₁/W₁ (4.8)
 = 272300/14107 = 19,3 кН/см²  R^св = 0,85×23 = 19,55кН/см².

Рисунок 4 – Изменение сечения балки по длине
5 Проверка и обеспечение общей устойчивости балки
Проверка прочности балки.

Проверяем максимальное нормальное напряжение в поясах в середине балки по формуле:
 = М_max/(С₁·W) (5.1)
 = 554040/(1,1·21898,8) = 23 кН/см²R = 23кН/см².
Проверяем максимальное касательное напряжение в стенке на опоре балки по формуле:
 = (Q_max·S₁)/(I₁·t_ст) (5.2)
 = (1231,2·8390,4)/(1114240·1,2) = 7,73 кН/см²< R = =13,5кН/см².
статический момент полусечения балки :
S₁ = b₁·t_п·(h₀/2)+((t_ст·h²_ст )/8) (5.3)
S₁ = 30·2·(158/2)+((1,2·156²)/8) = 8390,4 см³.
Проверяем местные напряжения в стенке под балками настила по формуле:
_м = F/(t_ст·l_м) (5.4)
_м = 113,88/(1,2·14) = 6,8 кН/см²  R
где F = 2·28,47·(4/2) = 113,88 кН,

l_м – длина передачи нагрузки на стенку балки.
l_м = b+2·t_п (5.5)
l_м = 11+(2·2) = 14см.
Проверяем приведенные напряжения в месте изменения сечения балки:
₁ = (М₁/W₁)·(h_ст/h) (5.6)
₁ = (272300/14107)·(156/160) = 18,82 кН/см².
₁ = (Q₁·S_п1)/(I₁·t_ст) (5.7)

₁ = (726·8390,4)/(1128562·1,2) = 4,5 кН/см².
S_п1 = b₁·t_п·(h₀/2) (5.8)
S_п1 = 30·2·(158/2) = 4740 см³.
_прив = ₁²+3₁² (5.9)
_прив = 19,1²+3·2,2² = 19,5кН/см² < 1,15R = 26,45кН/см².
Проверки показали, что прочность балки обеспечена.

Проверяем общую устойчивость балки в месте действия максимальных нормальных напряжений, принимая за расчетный пролет l₀ – расстояние между балками настила:

в середине пролета балки, где учтены пластические деформации, проверяем применимость формулы:
l = h/b_п (5.10)
l = 160/55 = 2,9  6
b_п/t_п = 55/2 = 27,5  35
 = 0,41+0,0032·b_п/t_п+(0,73-0,016b_п/t_п)·b_п/h₀·E/R (5.11)
 = 0,3·0,41+0,0032·55/2+ +(0,73-0,016·55/2)·55/158·2,06·10⁴/23 = 5,4

где  = 1-0,7·(с₁-1)/(с-1) = 0,3, т.к.  = 0 и с = с₁.

l₀/b_п = 85,7/55 = 1,56   = 5,4

В месте уменьшения сечения балки =1.

 =10,41+0,0032·30/2+(0,73-0,016·30/2)·30/158·2,06·10⁴/23 = 16,53

l₀/b₁ = 85,7/30 = 2,86   = 16,53
Обе проверки показали, что общая устойчивость балки обеспечена.

Проверка прогиба балки может не производиться, т.к. принятая высота балки больше минимальной h = 160см >154см.

6 Проверка и обеспечение местной устойчивости элементов балок

Проверяем устойчивость стенки. Первоначально определяем необходимость постановки ребер жесткости по формуле:

_ст = h_ст/t_ст·(R/E) (6.1)

_ст = 156/1,2·(23/2,06·10⁴) = 4,34  3,2,

т.е. вертикальные ребра жесткости необходимы.

Кроме того в зоне учета пластических деформаций необходимо постановка ребер жесткости под каждой балкой настила, т.к. местные напряжения в стенке в этой зоне недопустимы. Определяем длину зоны использования пластических деформаций в стенке по формуле:

а = l1–(1/c₁·h/h_ст) (6.2)

а = 18001–(1/1,1·160/156) = 468 см.

Т.к. _ст = 4,2  3,2 показывает что проверку устойчивости стенки нужно выполнять.

Проверяем отсек «а». в соответствии с формулой определяем среднее значение М и Q в сечении на расстоянии х = 171,4 см:
М₂ = q·х·(l-x)/2 (6.3)
М₂ = 121·1,714·(18–1,714)/2 = 1689 кН/м = 168900 кН/см.
Q₂ = q·(l/2-x) (6.4)
Q₂ = 121·(18/2-1,714) = 882 кН.
Определяем действующие напряжения:
 = (М₂/W)·(h_ст/h) (6.5)
 = (168900/21898,8)·(156/160) = 7,52 кН/см².
 = Q₂/(h_ст·t_ст) (6.6)
 = 882/(156·1,2) = 4,71 кН/см².
_м = 6,8 кН/см².
_м/ = 6,8/7,52 = 0,9
Определяем критические напряжения. По формуле находим:

_кр = 10,3(1+0,76/²)·(k_кр/²_усл) (6.7)
_кр = 10,3·(1+0,76/1,65²)·(13,5/4,34²) = 9,44 кН/см².
где h₀ = h_ст; _усл = _ст = 4,34;  = a/h₀ = 257,1/156 = 1,65 ; R_ср = 13,5кН/см².

Размеры отсека: a/h₀ =  = 1,65 и _м/ = 6,8/7,52 = 0,9

По формуле определяем:

 = ·b_п/h₀·(t_п/t_ст)³ (6.8)
 = 0,8·55/156·(2/1,2)³ = 1,39
По таблице, при  = 1,39 и a/h₀ = 1,65 предельное значение _м/ = 0,51. Расчетное значение _м/ = 0,9 > 0,51, поэтому _кр определяем по формуле:
_кр = (с_кр·R)/²_ст (6.9)
_кр = (32,2·23)/4,34² = 39,32 кН/см².
где с_кр = 32,2 – получено по таблице при  = 1,39.

По формуле определяем _м.кр., подставляя в нее из - таблицы значение а/2 вместо а:
_м.кр = (с₁·R)/ ²_а (6.10)
_м.кр = (14,5·23)/3,58² = 26,02 кН/см².
где

_а = а/(2·t_ст)·(R/E) (6.11)
_а = 257,1/(2·1,2)·23/2,06·10⁴ = 3,58
По таблице при  = 1,39 и a/2t_ст = 257,1/(2·156) = 0,82, с₁ = 14,5

Теперь подставляем все значения в формулу:
(/_кр+_м/_м.кр.)²+(/_кр)² = (7,52/39,32+6,8/26,02)²+(4,71/9,14)²= 0,67 < =1.
Проверка показала, что устойчивость стенки обеспечена.


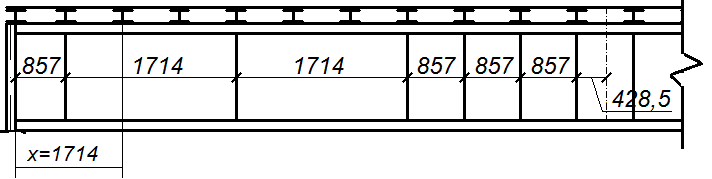
Рисунок 5 – Расстановка ребер жесткости

7 Соединение поясов балки со стенкой
Швы выполняются двухсторонние, автоматической сваркой в лодочку, сварочной проволокой Св-0,8А. определяем толщину шва в сечении, под первой от опоры балкой настила, где сдвигающая сила максимальная.
k_ш = 1/[n·(·R^у_св)min]·(Q·S_п/I)²+(F/l_м)² (7.1)
k_ш = 1/[2·(18,4)]·(1231,2·4740/1114240)²+(113,88/14)² = 0,26,
где S_п = b₁·t_п·(h₀/2) = 30·2·158/2) = 4740

По таблице определяем R^св_уш = 180Мпа = 18кН/см², а R^св_ус = 160Мпа = 16,0кН/см².

Принимаем по таблице минимально допустимый при толщине пояса t_п = 20мм, шов k_ш = 7мм, что больше получившегося по расчету k_ш = 2,6мм.

8 Стыки балок
Рассчитываем монтажный стык сварной балки на высокопрочных болтах.

Стык делаем в середине пролета балки, где М = 619650 кН·м и Q = 0.

Стык осуществляем высокопрочными болтами d=20мм из стали 40х «селект», имеющий R^н_в = 1100Мпа = 110 кН/см², обработка поверхности газопламенная. Несущая способность болта, имеющего две плоскости трения, находится:
Q^вб = R^вб_р·А^б_нт(_б·/_н)·k (8.1)
Q^вб = 77·2,45·0,85·(0,42/1,02)·2 = 132 кН
где R^вб_р = 0,7, R^н_в = 0,7×110 = 77 кН/см², А^б_нт = 2,45см², _б = 0,85, т.к разница в номинальных диаметрах отверстия и болта по углу закручивания к=2- две плоскости трения.

Стык поясов

Каждый пояс балки перекрыт тремя накладками сечениями 550×12мм и 2×250×12мм, общей площадью сечения:
А_н = 1,2·(55+2·25) = 126 см²А_п = 55·2 = 110 см².
Усилие в поясе определяем по формуле:
М_п = М·I_п/I (8.2)
М_п = 5540,04·1372262,4/1751904 = 4340 кН·м.
N_п = М_п/h₀ (8.3)
N_п = 4340/1,58 = 2747 кН.
Количество болтов для прикрепления накладок рассчитываем по формуле:
n = N_п/Q^вб (8.4)
n = 2747/132 = 20,8
По расчету принимаем 20 болтов, но по конструктивному решению окончательно принимаем 22 болта и размещаем их:

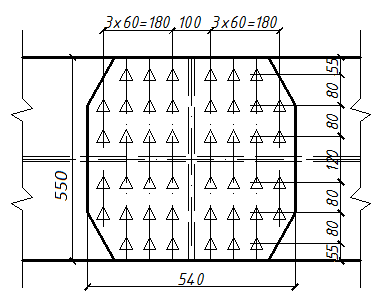
Рисунок 6 – Схема расположения болтов
Проверяем ослабление нижнего растянутого пояса отверстиями под болты d₀ = 22 мм (на 2мм больше диаметра болта). Пояс ослаблен двумя отверстиями по краю стыка.
А_п.нт = 2·(55-4·2,2) = 92,4 см²≈0,85А_п = 93,5 см².
Ослабление пояса можно не учитывать.

Проверяем ослабление накладок в середине стыка четырьмя отверстиями:
А^накл_нт = 126-6·2·1,2·2,2 = 94,32 см²0,85А_п = 93,5 см².
Стык стенки

Стенку перекрываем двумя вертикальными накладками сечением 320×1500×8мм. Момент, действующий на стенку, определяем по формуле:
М_ст = М·I_ст/I (8.5)
М_ст = 5540,04·379641,6/1751904 = 1201 кН/м.
Принимая расстояние между крайними по высоте рядами болтов а_max = 1400мм, где

а_max =h_стр – 2·80 = 1560 – 160 = 1400 мм
Принимаем 14 рядов с шагом 100. проверяем стык стенки по формуле:
N_max = М_ст·а_max/mа_i² (8.6)

N_max = 1201·1,4/2·5,6 = 150,13 кН > Q^вб = 132кН
где а_i² = 1,4²+1,2²+1 ²+0,8²+0,6²+0,4²+0,2² = 5,6 м²

Т.к условие не выполняется, принимаем диаметр болта 24мм.

Q^вб = R^вб_р·А^б_нт(_б·/_н)·k (8.7)
Q^вб = 77·3,52·0,85·(0,42/1,02)·2 = 189 кН.
Тогда N_max < Q^вб, условие выполняется.

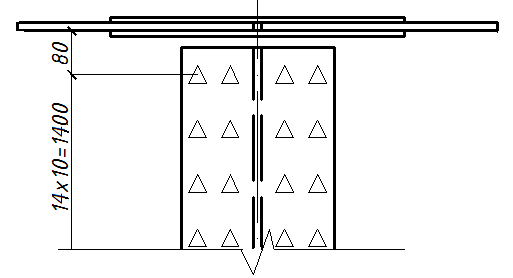
Рисунок 7 – Схема расположения болтов стенки
9 Опирание и сопряжение балок

Требуется рассчитать опорное ребро сварной балки. Опорная реакция балки F=1231,2 кН. Определяем площадь смятия торца ребра по формуле:
А_р = F/R_см.т (9.1)
А_р = 1231,2/34,5 = 35,7 см².
где R_см.т – расчетное сопротивление смятию торцевой поверхности, R_см.т = R_в = 345Мпа = 34,5кН/см².

Принимаем ребро 300×12мм, А_р = 30×1,2 = 36 см² > 35,7 см².

Проверяем опорную стойку балки на устойчивость относительно оси z. Ширина участка стенки, включенной в работу опорной стойки:
b_ст = 0,65·t_cт·E/R (9.2)
b_ст = 0,65·1,2·2.06·10⁴/23 = 23,34 см.
А_ст = А_р+t_ст·b_ст (9.3)
А_ст = 36+1,2·23,34 = 64 см².
I_z = 1,2·30³/12 +23,34·1,2³/12 = 2703 см⁴.

i_z = I_z/А_ст (9.4)
i_z = 2703/64 = 6,5 см.

 = h_cт/i_z (9.5)

 = 156/6,5 = 24, по приложению  = 0,951
 = F/·А_ст (9.6)
 = 1231,2/0,951·64 = 20,23 кН/см² < R=23кН/см².
Рассчитываем прикрепление опорного ребра к стенке балки двусторонними швами полуавтоматической сваркой проволокой Св-08Г2. предварительно находим параметры сварных швов и определяем минимальное значение R_у^св. принимаем R_уш^св = 215Мпа = 21,5кН/см²; R_ус^св = 160Мпа = 16,0кН/см²; _ш = 0,9; _с = 1,05; _ш × R_уш^св = 0,9×21,5 = 19,3кН/см² > _с × R_ус^св = 1,05×16 = 16,8 кН/см². Определяем катет сварных швов по формуле:
k_ш = (1/_c)·F/2·85·R_ус^св· R_ус (9.7)
k_ш = (1/1,05)·1231,2/2·85·16 = 0,64см
Принимаем катет шва k_ш = 7 мм. Проверяем длину рабочей части шва:
l_ш = 85_c· k_ш (9.8)
l_ш = 85·1,05·0,7 = 63 см < h_ст = 156см.
Ребро привариваем к стене по всей высоте сплошными швами.

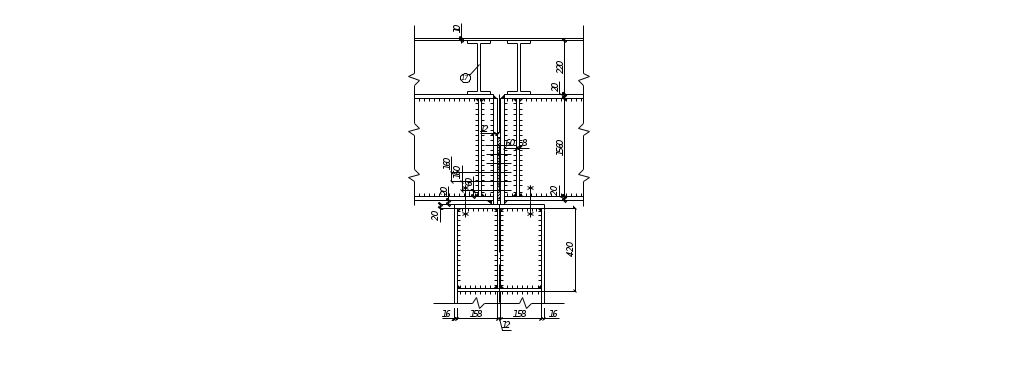
Рисунок 8 – Опирание балки на колонну.

10 Подбор сечения и конструктивное оформление стержня колонны
Требуется подобрать сечение сплошной центрально сжатой колонны длиной l = 6м, шарнирно закрепленная внизу и вверху. Материал – сталь ВСт3пс6-1, толщина листов t = 4-20 мм, R = 230 МПа = 23 кН/см². расчетное усилие в стержне колонны N = 2512 кН. Коэффициент условий работы  = 1. Принимаем двутавровое сечение стержня колонны сваренными из трех листов. Расчетная длина стержня l₀ = 1×6 = 6 м. задаемся гибкостью  = 70 и находим соответствующее значение  = 0,754, предварительно определив требуемые:

Площадь сечения:
А_тр = N/(·R) (10.1)
А_тр = 2512/(0,754·23) = 144,9 см²
Радиус инерции:
i_тр = l₀/ (10.2)
i_тр = 600/70 = 8,57 см.
Ширину сечения:

b_тр = i_тр/₂ (10.3)
b_тр = 8,57/0,24 = 35,7 см.
Принимаем сечение полки равное 2×36×1,6 = 115,2 см², стенки - 32,8×1,4 =45,92 см², А = 162 см².

Проверяем напряжение по подобранному сечению:
I_y = (2·1,6·36³)/12 = 1245 см⁴
i = 1245/162 = 7,7 см
 = 600/7,7= 78;  = 0,711
 = N/(·A) (10.4)
 = 2512/(0,711·162) = 21,8 кН/см²  23 кН/см².
Подобранное сечение удовлетворяет требованиям общей устойчивости. Проверяем местную устойчивость стенки по формуле:
 = R/E (10.5)
 = 7823/20600 = 2,6
h₀/t  (0,36+0,8·2,6²)20600/23 = 173  87 
стенка устойчива.

Проверяем местную устойчивость полки:
b₀/t_п = 17,3/1,6 = 10,8  (0,36+0,1·2,6) 20600/23 = 18,6
где b₀ = (36-1,4)/2 = 17,3

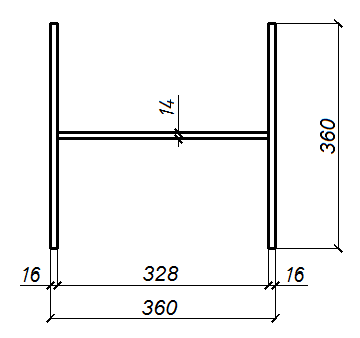
Рисунок 9 – Схема сечения колонны.
11 Расчет и конструктивное оформление баз с траверсой и консольными ребрами
Запроектировать базу сплошной колонны двутаврового сечения. Материал базы – сталь марки Вст3кп2, расчетное сопротивление R = 205Мпа = 21кН/см² при t = 21-40мм. Бетон фундамента марки 150, R_пр = 7Мпа = 0,7кН/см². Нагрузка на базу N = 2512 кН.

Требуемая площадь плиты базы:
А_пл.тр. = N/R_пр· (11.1)
А_пл.тр. = 2512/0,7·1,2= 2990 см²
По ориентировочному значению коэффициент  = 1,2 принимаем плиту размером 560×560мм. Принимая площадь по обрезу фундамента 800×800см, корректируем коэффициент :
 = А_ф/А_пл (11.2)
 = 80·80/56·56 = 1,4
Далее рассчитываем напряжение под плитой базы:
_ф = 2512/56·56 = 0,7 кН/см²  R_пр = 0,7×1,4 = 0,98 кН/см².
Конструируем базу колонны с траверсами толщиной 12 мм, привариваем их к полкам колонны и к плите угловыми швами. Вычисляем изгибающие моменты на разных участках для определения толщины плиты.

Участок 1, опертый на 4 канта.

Отношение сторон b/a = 328/173 = 1,9;  = 0,098:
М_пл.1 = ·q·а² (11.3)
М_пл.1 = 0,098·0,7·17,3² = 20,5 кН·см;
Участок 2, консольный, отношение b/a˃2
М₃ = (q·l²)/2 (11.4)
М₃ = (0,7·10²)/2 = 35 кН·см.
Участок 3 не проверяем, так как он имеет меньший консольный свес. Определяем толщину плиты по максимальному моменту:
t_пл  6·М_max/R (11.5)
t_пл = 6·35/21 = 3,16 см.
Принимаем плиту толщиной t_пл = 32 мм.

Таким образом, с запасом прочности усилие в колонне полностью передается на траверсы, не учитывая прикрепления торца колонны к плите.

Прикрепление траверсы к колонне выполняются полуавтоматической сваркой в углекислом газе сварочной проволокой Св08Г2С. Толщину траверс принимаем t_тр = 12мм, высоту h_тр = 400мм. Расчетные характеристики: R_уш^св = 215МПа = 21,5кН/см²; R_ус^св = 0,45×365 = 164,2МПа = 16,42кН/см²; _ш = 0,7; _с = 1,0; _ш R_уш^св = 0,7×21,5 = 15,05кН/см² < _с R_ус^св = 1×16,42 = 16,42кН/см²;  _уш^св = _ус^св = 1.

Прикрепления рассчитываем по металлу шва, принимая катет угловых швов k_ш =12мм:
_ш = N/( k_ш·4l_ш) (11.6)
_ш = 2512/(1,2·4·38) = 13,8 кН/см²  15,05кН/см².
Проверяем допустимую длину шва:
l_ш = (40-2) = 38см < 85·_ш k_ш = 85·0,7·1,2 = 71,4см.
Требование к максимальной длине швов выполняется. Крепление траверсы к плите принимаем угловыми швами k_ш =10 мм.
Проверяем прочность швов:
_ш = N/ k_ш·l_ш (11.7)
_ш = 2512/1·2(54+2·8+2·30,8) = 9,54 кН/см²  15,05кН/см².
Швы удовлетворяют требованиям прочности. При вычислении суммарной длины швов с каждой стороны шва не учитывалось по 1см на непровар.

Приварку торца колонны к плите выполняем конструктивными швами k_ш = 6 мм, т.к. эти швы в расчете не учитывались.

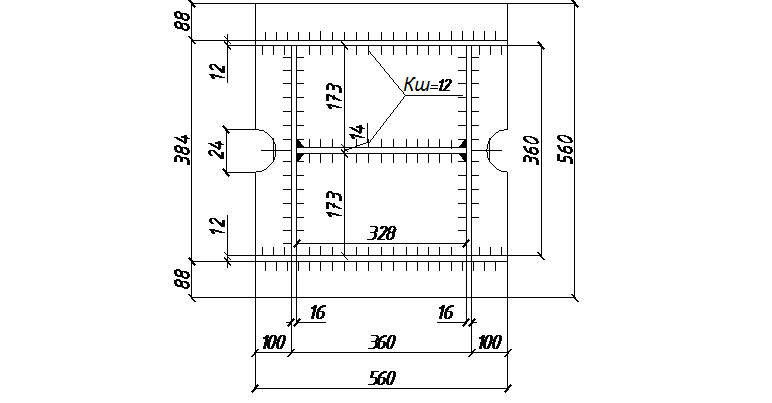
Рисунок 10 – Сечение базы сплошной колонны
12 Конструирование и расчет оголовков колонн
Высоту ребра оголовка определяют требуемой длиной швов, передающих нагрузку на стержень

h_р = N/4 k_ш·(_у^св ·R_у^св)_min (12.1)
h_р = 2512/4·1·15,05·1 = 41,7 см
Принимаем h_р = 42 см

Толщину ребра оголовка определяют из условия сопротивления на смятие под полным давлением:

t_р = N/l_см·R_см.т (12.2)

t_р = 2512/(30+2·20)·35 = 1,03

принимаем t_р = 12 мм.

Назначив толщину ребра, следует проверить его на срез по формуле:
 = 0,5·N/2·h_р·t_р  R_ср (12.3)
 = 0,5·2512/2·42·1,2 = 12,4  R_ср = 13,5кН/см².
Столик целесообразно приваривать к колонне по трем сторонам.

Сварные швы, приваривающие столик к колонне, рассчитывают по формуле:
 = N/ k_ш·l_ш  (_у^св· R_у^св)_min (12.4)
 = 2512/1,2(15,3·8+13,8·4) = 11,8  15,05

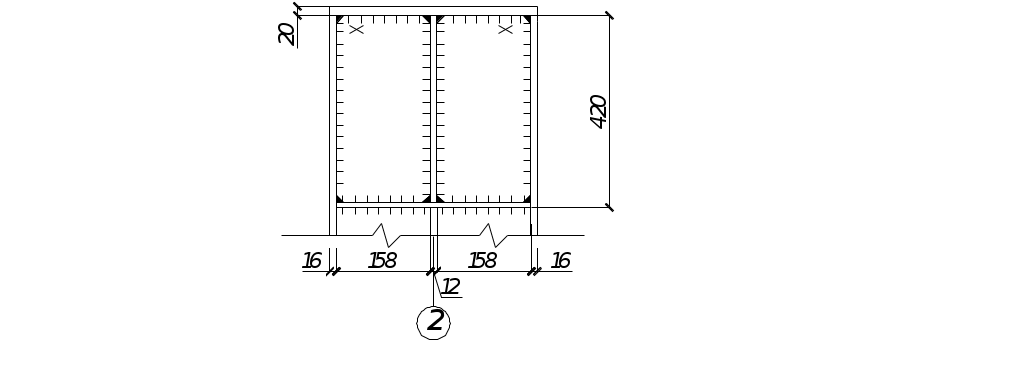
Рисунок 11 – Схема приваривания столика к колонне

Заключение
Курсовая работа выполнена на проектирование балочной клетки одноэтажного промышленного здания, в полном объеме и в соответствии с заданием. После расчета настила, была скомпонована балочная клетка и по расчету, был выбран вариант с меньшим расходом металла. Произведен расчет и проектирование главной балки: подбор сечения, изменения сечения сварной балки, проверка и обеспечение общей устойчивости балки, местной устойчивости элементов балок. Рассчитаны болтовые соединения на стыках поясов и стенок балок. По расчету были подобранны размеры и сконструированы двутавровая колонна, ее база с траверсами и оголовок.

Содержание

Введение	4
1 Расчет настила	5
2 Компоновка балочной клетки и расчет балок настила	6
3 Подбор сечения балок	10
4 Изменение сечения сварной балки	14
5 Проверка и обеспечение общей устойчивости	16
6 Проверка и обеспечение местной устойчивости элементов балок	18
7 Соединение поясов балки со стенкой	21
8 Стыки балок	22
9 Опирание и сопряжение балок	25
10 Подбор сечения и конструктивное оформление стержня колонны	27
11 Расчет и конструктивное оформление баз с траверсой и консольными ребрами	29
12 Конструирование и расчет оголовков колонн	32
Заключение	33
Список использованных источников	34

Список использованных источников

1. 
   Беленя Е. И. Металлические конструкции. М.:Стройиздат, 1986-559 с.
   
2. 
   Горшкова Л. В. «Расчет и проектирование балочной клетки» учебное пособие. 2014 г.
   
3. 
   СНиП РК 5.04-23-2002 «Стальные конструкции». Нормы проектирования. г. Астана. Комитет по делам строительства Министерства индустрии и торговли 2002 г.