МК КРИС. 1 Вывод 11 Расчет сварных швов настила с балкой настила 50
 Скачать 487.5 Kb. Скачать 487.5 Kb.
|
Оглавление1.2.4.Вывод 11 3.Расчет сварных швов настила с балкой настила 50 4.Расчет поясных швов 51 4.1.Расчет поясных соединений 51 4.2.Расчет крепления опорного ребра к стенке главной балки 53 5.Расчет крепления балки настила к главной балке 54 6.Расчет монтажного стыка главной балки 56 6.1.Болтовой стык пояса 56 7.Уточнение собственного веса главной балки 60 8.2.Подбор сечений стержня 62
Производится конструирование и расчёт стальной балочной клетки рабочей площадки промышленного здания со следующими исходными данными:
(пролет главной балки) – L=11,8м;
Размеры настила при работе его на изгиб с учётом распора Н можно приближенно вычислить из условия заданного предельного прогиба (II группа предельных состояний) по формуле: 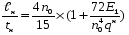 , ,где lн — пролет настила; tн – толщина настила; n0=[l/f] — отношение пролёта настила к его предельному прогибу, величина, обратная предельному значению относительного прогиба конструкции (для стального настила рабочих площадок производственных зданий при отсутствии крановых путей [f/l]=1/150 ). Е1 – приведённый модуль упругости стали; �� — коэффициент Пуассона для стали; qн – нормативное значение нагрузки, воспринимаемое сталью. 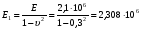 (кгс/см2) (кгс/см2)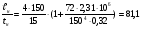 (см/см) (см/см)Для tн=8мм: 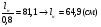 Число шагов балок будет равно: 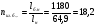 Примем 18 шагов и, следовательно, 19 балок настила с шагом Примем 18 шагов и, следовательно, 19 балок настила с шагом 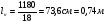 Для tн=10мм: 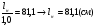 Число шагов балок будет равно: 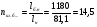 Примем 15 шагов и, следовательно, 16 балок настила с шагом Примем 15 шагов и, следовательно, 16 балок настила с шагом 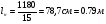 Для tн=12мм: 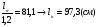 Число шагов балок будет равно: 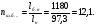 Примем 12 шагов и, следовательно, 13 балок настила с шагом Примем 12 шагов и, следовательно, 13 балок настила с шагом 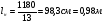
Расчет балки настила производится как для балок 2-3 класса, т.е. по упруго-пластической стадии. 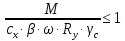 Рассчитаем собственный вес настила по формуле: 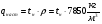 Для определения интенсивности распределенной нагрузки, действующей на БН, необходимо все нагрузки привести к погонным (кН/м2). Ширина грузовой площади балок настила равна их шагу а. Нормативное значение нагрузки, действующей на БН: 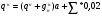 (3) (3)Расчётное значение нагрузки, действующей на БН: 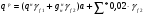 , где (4) , где (4)f1=1,2 коэффициент надёжности по временной нагрузке; f2=1,05 – коэффициент надёжности по нагрузке от собственного веса. Рассмотрим толщину настила в 8мм: 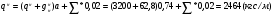 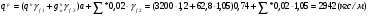 Рассмотрим толщину настила в 10мм: Рассмотрим толщину настила в 10мм: 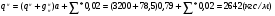 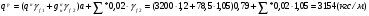 Рассмотрим толщину настила в 12мм: Рассмотрим толщину настила в 12мм: 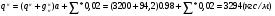 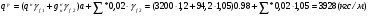
Требуемый момент сопротивления поперечного сечения балки равен: 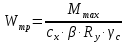 Rу=325Мпа=3250кгс/см2 –расчетное сопротивление материала балки по пределу текучести (для стали С345). ��с=1 –коэффициент условий работы. 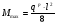 , ,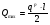 Рассмотрим толщин у настила в 8мм: 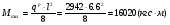 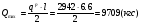 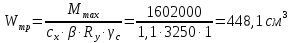 №30Б2, имеющий Wx=487,8см3, Jx=7293см4, mбн=36,6кг/м Рассмотрим толщину настила в 10мм: 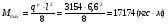 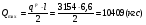 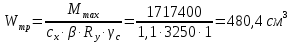 №35Б1, имеющий Wx=581,7см3, Jx=10060см4, mбн=38,9кг/м Рассмотрим толщину настила в 12мм: 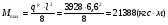 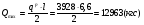 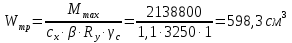 №35Б2, имеющий Wx=662,2 см3, Jx=11550см4, mбн=43,3 кг/м
Рассмотрим толщину настила в 8мм: 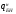 =3200 =3200 0,74+62,8 0,74+62,8  0,74+36,6=2451кг/м 0,74+36,6=2451кг/м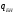 =3200 =3200 0,74 0,74 1,2+62,8 1,2+62,8  0,74 0,74 1,05+36,6·1,05=2929 кг/м 1,05+36,6·1,05=2929 кг/м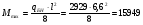 кг кг м м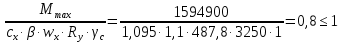 =>условие прочности выполняется. =>условие прочности выполняется.β=1 cx=1,095, из приложения Е. Аf=14·1=14см2, Аw=А-Аf·2=46.67-14·2=18.67 см2. 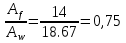 . .Рассмотрим толщину настила в 10мм: 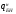 =3200 =3200 0,79+78,5 0,79+78,5  0,79+38,9=2630кг/м 0,79+38,9=2630кг/м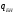 =3200 =3200 0,79 0,79 1,2+78,5 1,2+78,5  0,79 0,79 1,05+38,9·1,05=3141 кг/м 1,05+38,9·1,05=3141 кг/м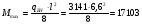 кг кг м м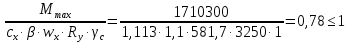 =>условие прочности выполняется. =>условие прочности выполняется.β=1 cx=1,113, из приложения Е. Аf=15,5·0,85=13,2см2, Аw=А-Аf·2=49,53-13,2·2=23,13см2. 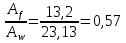 . .Рассмотрим толщину настила в 12мм: 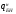 =3200 =3200 0,98+94,2 0,98+94,2  0,98+43,3=3272кг/м 0,98+43,3=3272кг/м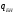 =3200 =3200 0,98 0,98 1,2+94,2 1,2+94,2  0,98 0,98 1,05+43,3·1,05=3906 кг/м 1,05+43,3·1,05=3906 кг/м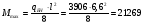 кг кг м м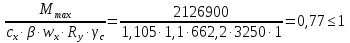 =>условие прочности выполняется. =>условие прочности выполняется.β=1 cx=1,105, из приложения Е. Аf=15,5·1 =15,5см2, Аw=А-Аf·2=55,17-15,5·2=24,17см2. 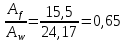 . .
Рассмотрим толщину настила в 8мм: 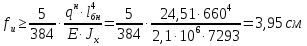 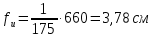 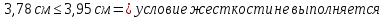 Рассмотрим толщину настила в 10мм: 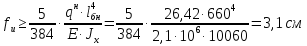 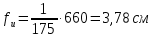 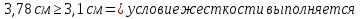 Рассмотрим толщину настила в 12мм: 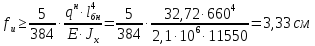 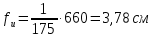 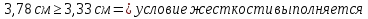
Вариант №1 не проходит проверку жесткости, а принимать двутавр большего сечения не является верным решением, т.к. он удовлетворяет для пролета настила толщиной 10мм. Вариант №2 проходит проверку прочности с меньшим запасом, чем вариант №3. Для расчета принимаем вариант №2. Для балок настила принимаем двутавр №35Б1, имеющий следующие геометрические характеристики: Wx=581,7см3, Jx=10060см4, h=346мм, А=49,53см2, b=155мм, s=6,2мм, t=8,5мм, собственный вес m=38,9кг/м.
Учитывая принятый шаг балок настила lбн=79см, определяем что их количество n=16 штук. Т.к. n=16≥5, то принимаем их за равномерно распределенную нагрузку. Расчетное значение нагрузки действующей на БН 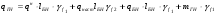 где: f1=1,2 f2=1,05 – для металлических конструкций mГБ принимаем равным 2% от всей действующей нагрузки. 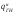 =3200 =3200 6,6+78,5 6,6+78,5  6,6+38,9·6,6+(3200 6,6+38,9·6,6+(3200 6,6+78,5 6,6+78,5  6,6+38,9·6,6)·0,02=22027.5+440.5=22468 кг/м 6,6+38,9·6,6)·0,02=22027.5+440.5=22468 кг/м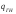 =3200 =3200 6,6·1,2+78,5 6,6·1,2+78,5 6,6·1,05+38,9·6,6·1,05+(3200 6,6·1,05+38,9·6,6·1,05+(3200 6,6+78,5 6,6+78,5  6,6+38,9·6,6)·0,02·1,05=26296,9+462,5=26759,4 кг/м 6,6+38,9·6,6)·0,02·1,05=26296,9+462,5=26759,4 кг/м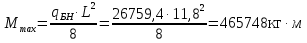 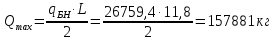 
Внутренние усилия, возникающие в ГБ, значительны, в результате чего использование прокатных профилей не практично. Поэтому ГБ проектируется составной. Как правило, составные балки проектируются сварными, а сечение составных балок напоминает сечение прокатных двутавров: один вертикальный лист стали образует стенку двутавра, два горизонтальных листа образуют его полки. Исходя из полученных данных подбираем прокатный двутавр 100Б4, но данный двутавр является спец серией и применять его не практично.
Определяющим в компоновке сечения ГБ является подбор размеров стенки балки – высоты и толщины. Высота ГБ, основную часть которой составляет высота стенки, определяется по экономическим соображениям, жёсткости балки и допустимой строительной высоте конструкции перекрытия. Толщина стенки балки также определяется несколькими факторами и соответственно имеет несколько значений – минимальное, принимаемое из условия работы ГБ на касательные напряжения, и рациональное, принимаемое из экономических соображений. Предварительное значение высоты балки принимаем равным: 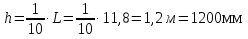 Предварительное значение толщины стенки принимаем равным: 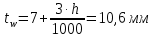 Принимаем по ГОСТ 19903-74 tw=11мм. Оптимальную высоту балки определяем по формуле: 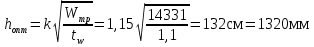 Где k-коэффициент, зависящий от конструктивного оформления балки, для сварных балок k=1,15 Наименьшая рекомендуемая высота балки h определяется жесткостью балки - ее продольным прогибом (второе предельное состояние). Для балки равномерно нагруженной по длине: 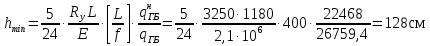 [l/f]=400; Е=2,1*106 кг/см2 – модуль упругости стали; Ry =3250 кгс/см2 – расчётное сопротивление материала балки по пределу текучести. Сравнивая полученные данные, принимаем высоту балки, близкую к оптимальной с учетом сортамента листовой стали h=140 см. Лист принимаем не окантованный. Уточнение толщины стенки 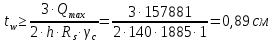 Найдем толщину стенки из условия не постановки продольных ребер жесткости: 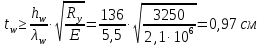
Толщину полки принимаем не более 2-х/3-х толщин стенки, но не более 30 мм: 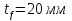 Ширина полки главной балки определяется из требуемого значения площади сечения полки. Формулу для определения площади сечения одной полки можно получить из известной формулы Штейнера, которая позволяет определять моменты инерции сложных относительно осей, не совпадающих с нейтральной осью всего сечения: 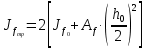 , где , гдеJfтр – требуемый момент инерции сечения двух полок относительно нейтральной оси балки; Af – площадь сечения одной полки; h0/2 – расстояние от нейтральной оси балки до собственной оси полки. Ввиду малости значения, моментом инерции сечения полки относительно собственной оси можно пренебречь. Расчет проводим по формуле: 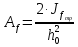 . .Требуемый момент инерции сечения одной полки относительно нейтральной оси балки определится как разность между требуемым моментом инерции всего сечения балки и фактическим моментом инерции стенки балки: 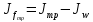 , где , гдеJw – момент инерции сечения стенки балки; Jтр- требуемый момент инерции всего сечения. 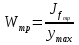 , выразим отсюда момент инерции: , выразим отсюда момент инерции: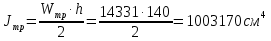 Момент инерции стенки балки определяется как момент инерции прямоугольного сечения: 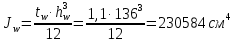 ; ;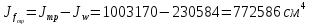 ; ;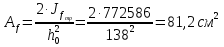 . .Толщина листа принята tf =2см, 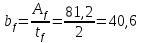 см. см.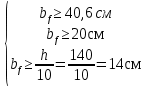 По ГОСТ 82-70 принимаем ширину листа стали 420 мм. Проверка местной устойчивости сжатой полки: 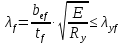 ; ;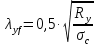 ; ;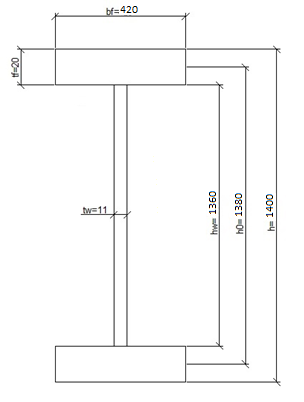 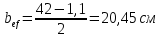 ; ;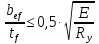 ; ;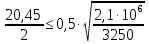 ; ;10,23≤12,7 Условие выполняется, значит, принятые размеры главной балки удовлетворяют условиям местной устойчивости. Имеем следующее сечение главной балки: 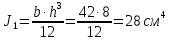 . .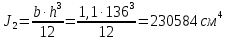 . .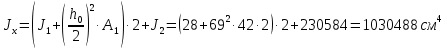 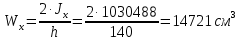 . .
Поскольку изгибающий момент уменьшается от середины к опорам балки, то вместе с ним уменьшаются и нормальные напряжения. Поперечное сечение балки на опорах можно уменьшить в целях экономии материала. При равномерно распределенной нагрузке наиболее выгодное по расходу стали место изменения сечения поясов однопролетной сварной балки находится на расстоянии 1/6 пролета балки от опоры 1/6L=1/611,8=1,97м. Примем на расстоянии 2 м.
Мx=Qmax·x-0,5·qГБ·x2=157881·2-0,5·26759,4 ·22=262243 кг·м Qmax=157881 кг
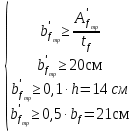 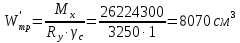 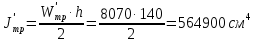 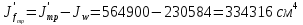 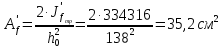 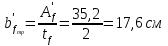 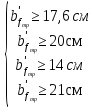 По ГОСТ 82-70 принимаем ширину листа стали 220 мм. Имеем следующее сечение главной балки: 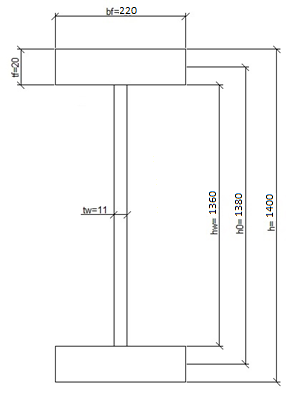 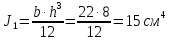 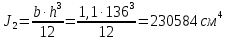 . .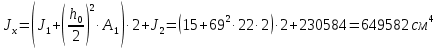 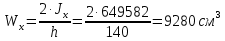 . .
Проверку прочности по нормальным напряжениям элементов, изгибаемых в одной из главных плоскостей, следует выполнять по формуле: 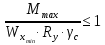 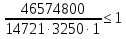 0,97≤1. Прочность главной балки по нормальным напряжениям обеспечена. Недонапряжение в главной балке 3% удовлетворяют требованиям норм. Проверка прочности по касательным напряжениям элементов, изгибаемых в одной из главных плоскостей, выполняем для измененного сечения: 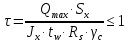 Q – максимальное по длине балки значение поперечной силы; J – момент инерции сечения балки, в котором возникает поперечная сила, для измененного сечения; S - статический момент измененного полусечения балки, относительно оси, проходящей через нейтральную линию; t – толщина стенки балки. 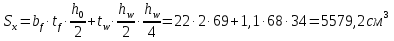 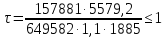 0,66≤1 Прочность балки по касательным напряжениям обеспечена. Проверка прочности на совместное действие касательных и нормальных напряжений: По всей длине главной балки (за исключением сечений, в которых M или Q равны нулю), изгибающий момент и поперечная сила действуют совместно. Поэтому, помимо раздельных проверок на нормальные и касательные напряжения, необходима проверка совместного действия этих напряжений, при которой определяются приведенные напряжения. 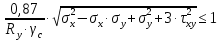 σx- нормальные напряжения в серединной плоскости стенки, параллельные к оси балки; σy=σloc - нормальные напряжения в серединной плоскости стенки, перпендикулярные оси балки, определяется по формуле; τxy - касательное напряжение, воспринимаемое стенкой.
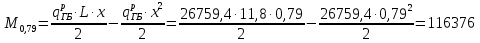 кг·м кг·м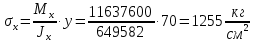 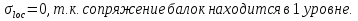 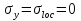 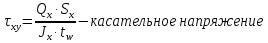 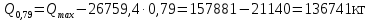 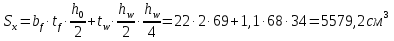 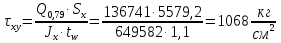 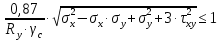 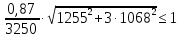 0,6≤1 – прочность сечения ГБ на совместное действие нормальных и касательных напряжений обеспечена.
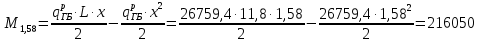 кг·м кг·м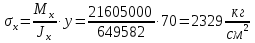 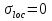 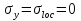 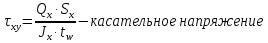 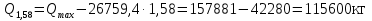 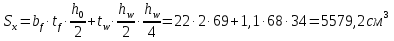 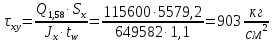 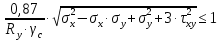 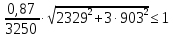 0,75≤1 – прочность сечения ГБ на совместное действие нормальных и касательных напряжений обеспечена.
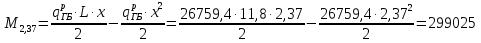 кг·м кг·м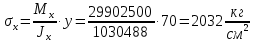 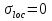 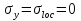 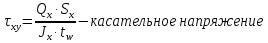 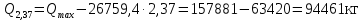 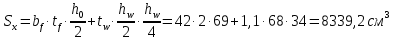 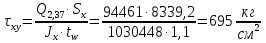 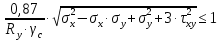 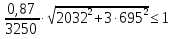 0,64≤1 – прочность сечения ГБ на совместное действие нормальных и касательных напряжений обеспечена.
Проверка общей устойчивости главной балки осуществляется в соответствии с требованиями норм. Проверку общей устойчивости можно не проводить, если соблюдены требования норм: - при передачи нагрузки через сплошной жесткий настил, непрерывно опирающийся на сжатый пояс балки и надежно с ним связанный; - при отношении расчетной длины балки к ширине сжатого пояса, не превышающем нормативных значений, для балок симметричного двутаврового сечения и с более развитым сжатым поясом, для которых ширина растянутого пояса составляет не менее 3 /4 ширины сжатого пояса. Наибольшее значение, при котором не требуется расчет на устойчивость сварных балок в случае приложения нагрузки к верхнему поясу балки, определяем по формуле: Расчет на общую устойчивость ведется согласно пункту 8.4.4 [1]. 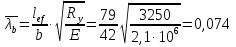 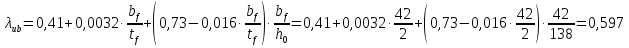 0,07≤0,597 Условие выполняется, значит, общую устойчивость главной балки проверять не требуется. За расчетную длину балки следует принимать расстояние между точками закрепления сжатого пояса от поперечных смещений. В данном случае за расчетную длину ГБ следует принять шаг балок настила.
Проверка и обеспечение местной устойчивости стенки ГБ выполняется в зависимости от значения условной гибкости стенки, которая определяется по следующей формуле: 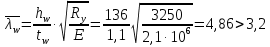 Значение условной гибкости стенки превышает 3.2, поэтому следует проверить устойчивость стенки балки. При этом следует устанавливать поперечные основные ребра жесткости согласно требованиям п8.5. Расстояние между основными поперечными ребрами жесткости не должно превышать 2·hef при 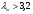 : :a≤2·hw=2·136=272(см). Расстояние между ребрами жесткости принимаем 0,79м– расстояние равное шагу БН. Первый отсек: Местную устойчивость стенки проверим в 1-м отсеке. Расчетным сечением будет середина 1 отсека, она находится на расстоянии х=0,395 м от опоры. Изгибающий момент и поперечная сила в этом сечении будут равны: 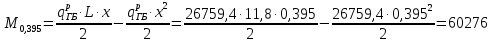 кг·м кг·м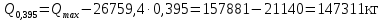 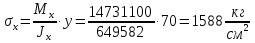 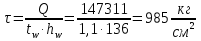 Определим критические значения напряжений: 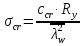 Ccr –определяется из таб.12 [1] и зависит от δ. 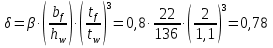 При помощи линейной интерполяции находим ccr=30. 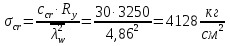 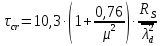 �� равно отношению большей стороны отсека к меньшей: 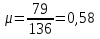 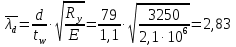 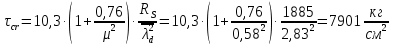 Расчет на устойчивость стенок балок симметричного сечения, укрепленных только поперечными основными ребрами жесткости, при наличии местного напряжения следует выполнять по формуле (80) [1]: 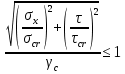 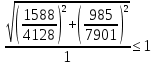 0,41≤1. В крайних отсеках проверка местной устойчивости стенки выполнена. Второй отсек: Местную устойчивость стенки проверим во 2-м отсеке. Расчетным сечением будет середина второго отсека, она находится на расстоянии х=1,185 м от опоры. Изгибающий момент и поперечная сила в этом сечении будут равны: 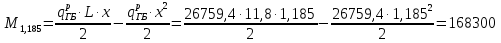 кг·м кг·м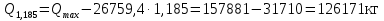 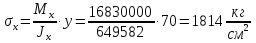 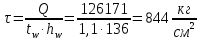 Определим критические значения напряжений: 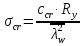 Ccr –определяется из таб.12 [1] и зависит от δ. 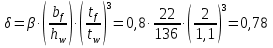 При помощи линейной интерполяции находим ccr=30. 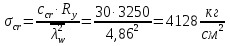 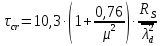 �� равно отношению большей стороны отсека к меньшей: 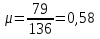 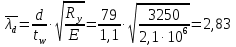 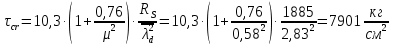 Расчет на устойчивость стенок балок симметричного сечения, укрепленных только поперечными основными ребрами жесткости, при наличии местного напряжения следует выполнять по формуле (80) [1]: 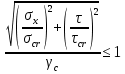 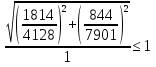 0,46≤1. В крайних отсеках проверка местной устойчивости стенки выполнена. Третий отсек: Местную устойчивость стенки проверим в 3-м отсеке. Местную устойчивость стенки проверим во третьем отсеке. Расчетным сечением будет середина второго отсека, она находится на расстоянии х=1,975 м от опоры. Изгибающий момент и поперечная сила в этом сечении будут равны: 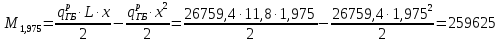 кг·м кг·м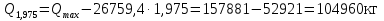 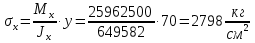 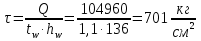 Определим критические значения напряжений: 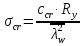 Ccr –определяется из таб.12 [1] и зависит от δ. 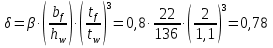 При помощи линейной интерполяции находим ccr=30. 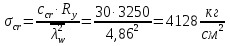 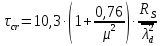 �� равно отношению большей стороны отсека к меньшей: 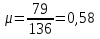 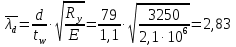 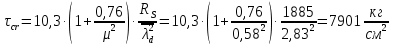 Расчет на устойчивость стенок балок симметричного сечения, укрепленных только поперечными основными ребрами жесткости, при наличии местного напряжения следует выполнять по формуле (80) [1]: 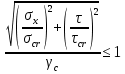 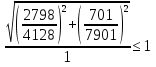 0,69≤1. В крайних отсеках проверка местной устойчивости стенки выполнена. Четвертый отсек: Местную устойчивость стенки проверим в 4-м отсеке. Расчетным сечением будет сечение, находящееся в центральной части отсека, оно находится на расстоянии х=2,765 м от опоры. Изгибающий момент и поперечная сила в этом сечении будут равны: 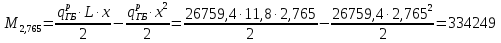 кг·м кг·м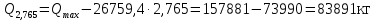 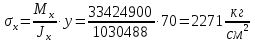 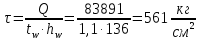 Определим критические значения напряжений: 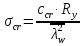 Ccr –определяется из таб.12 [1] и зависит от δ. 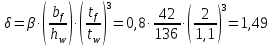 При помощи линейной интерполяции находим ccr=32,4. 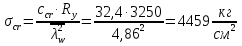 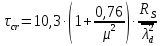 �� равно отношению большей стороны отсека к меньшей: 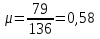 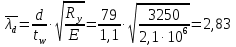 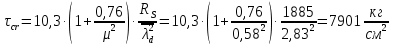 Расчет на устойчивость стенок балок симметричного сечения, укрепленных только поперечными основными ребрами жесткости, при наличии местного напряжения следует выполнять по формуле (80) [1]: 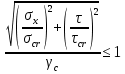 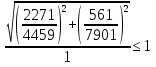 0,52≤1. В крайних отсеках проверка местной устойчивости стенки выполнена. Пятый отсек: Местную устойчивость стенки проверим в 5-м отсеке. Расчетным сечением будет сечение, находящееся в центральной части отсека, который совпадает с центом балки, оно находится на расстоянии х=3,555 м от опоры. Изгибающий момент и поперечная сила в этом сечении будут равны: 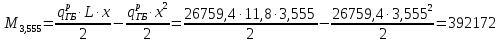 кг·м кг·м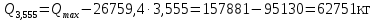 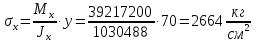 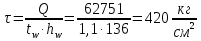 Определим критические значения напряжений: 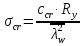 Ccr –определяется из таб.12 [1] и зависит от δ. 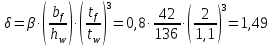 При помощи линейной интерполяции находим ccr=32,4. 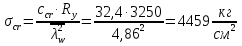 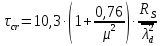 �� равно отношению большей стороны отсека к меньшей: 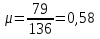 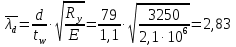 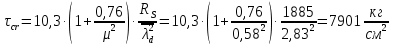 Расчет на устойчивость стенок балок симметричного сечения, укрепленных только поперечными основными ребрами жесткости, при наличии местного напряжения следует выполнять по формуле (80) [1]: 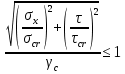 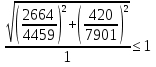 0,6≤1. В крайних отсеках проверка местной устойчивости стенки выполнена. Шестой отсек: Местную устойчивость стенки проверим в 6-м отсеке. Расчетным сечением будет сечение, находящееся в центральной части отсека, который совпадает с центом балки, оно находится на расстоянии х=4,345 м от опоры. Изгибающий момент и поперечная сила в этом сечении будут равны: 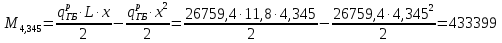 кг·м кг·м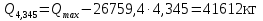 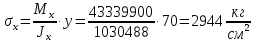 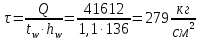 Определим критические значения напряжений: 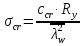 Ccr –определяется из таб.12 [1] и зависит от δ. 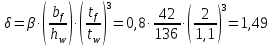 При помощи линейной интерполяции находим ccr=32,4. 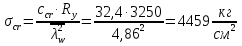 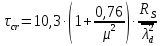 �� равно отношению большей стороны отсека к меньшей: 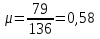 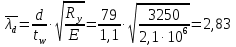 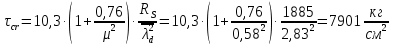 Расчет на устойчивость стенок балок симметричного сечения, укрепленных только поперечными основными ребрами жесткости, при наличии местного напряжения следует выполнять по формуле (80) [1]: 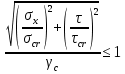 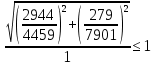 0,67≤1. В крайних отсеках проверка местной устойчивости стенки выполнена. Седьмой отсек: Местную устойчивость стенки проверим в 7-м отсеке. Расчетным сечением будет сечение, находящееся в центральной части отсека, который совпадает с центом балки, оно находится на расстоянии х=5,135 м от опоры. Изгибающий момент и поперечная сила в этом сечении будут равны: 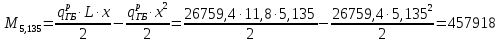 кг·м кг·м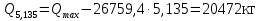 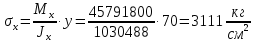 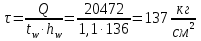 Определим критические значения напряжений: 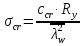 Ccr –определяется из таб.12 [1] и зависит от δ. 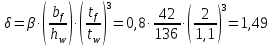 При помощи линейной интерполяции находим ccr=32,4. 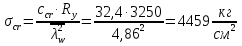 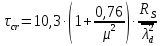 �� равно отношению большей стороны отсека к меньшей: 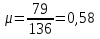 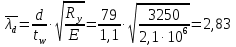 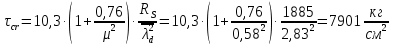 Расчет на устойчивость стенок балок симметричного сечения, укрепленных только поперечными основными ребрами жесткости, при наличии местного напряжения следует выполнять по формуле (80) [1]: 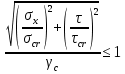 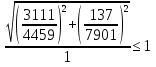 0,7≤1. В крайних отсеках проверка местной устойчивости стенки выполнена. Восьмой отсек: Местную устойчивость стенки проверим в 8-м отсеке. Расчетным сечением будет сечение, находящееся в центральной части отсека, который совпадает с центом балки, оно находится на расстоянии х=5,9 м от опоры. Изгибающий момент и поперечная сила в этом сечении будут равны: 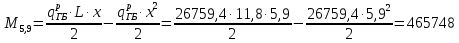 кг·м кг·м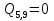 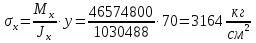 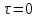 Определим критические значения напряжений: 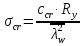 Ccr –определяется из таб.12 [1] и зависит от δ. 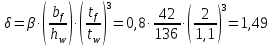 При помощи линейной интерполяции находим ccr=32,4. 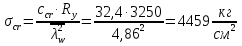 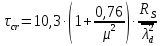 �� равно отношению большей стороны отсека к меньшей: 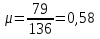 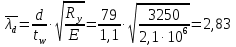 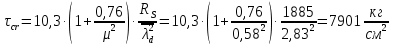 Расчет на устойчивость стенок балок симметричного сечения, укрепленных только поперечными основными ребрами жесткости, при наличии местного напряжения следует выполнять по формуле (80) [1]: 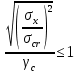 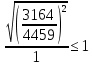 0,71≤1. В крайних отсеках проверка местной устойчивости стенки выполнена.
Устойчивость сжатых поясов следует считать обеспеченной, если условная гибкость свеса пояса не превышает предельных значений, определяемых по формуле (97) [1]. 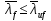 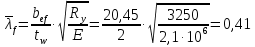 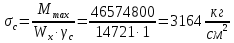 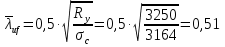 0,41≤0,51 Устойчивости полки обеспечена, согласно п.8.5.18 [1].
Расчет ведется по второй группе предельных состояний, поэтому учитываем нормативное значение нагрузки qгбн=22468 кг/м. f≤fu. 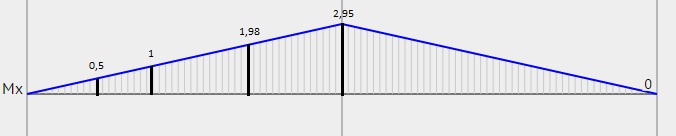 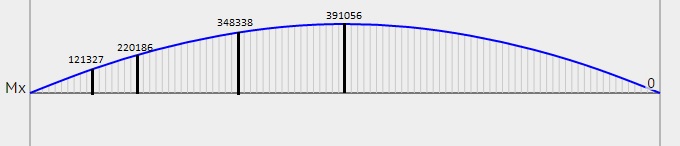 Jх=1030488 см4; l=390см Jх=1030488 см4; l=390смJ’x=649582 см4; l’=200 см 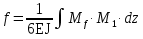 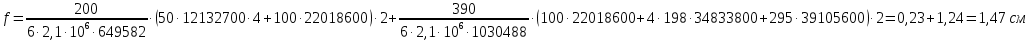 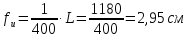 1,47 см≤2,95см Проверка прогиба балки выполняется.
Укрепляем стенку парными симметричными ребрами. Ширина выступающей части ребра: 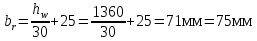 Толщина ребра, должна быть не менее выражения: 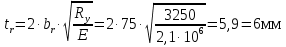
Согласно п.8.5.17 [1], при высоте выступающей части опорного ребра 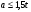 =24, напряжения в нижних торцах при действии опорной реакции не должны превышать расчетного сопротивления стали смятию =24, напряжения в нижних торцах при действии опорной реакции не должны превышать расчетного сопротивления стали смятию 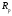 . Из условия смятия определяется необходимая площадь поперечного сечения опорного ребра. . Из условия смятия определяется необходимая площадь поперечного сечения опорного ребра. Назначаем размер толщины ребра из условия: 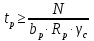 Ширину опорного ребра примем равной ширине полки. bр=b’f=22см 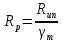 Run=470 H/мм2 (В.5,[1]) ��m=1,025 –коэффициент надежности по материалу. 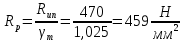 N=RГБ=Qmax=157881кг  10,2=1610387 Н 10,2=1610387 Н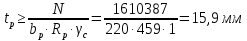 Принимаем tp= 16мм при bp=220мм. Ар=16·220=3520мм2 Согласно СП, п.8.5.17 участок стенки балки составного сечения над опорой при укреплении его ребрами жесткости следует рассчитывать на продольный изгиб из плоскости как стойку, нагруженную опорной реакцией. В расчетное сечение этой стойки следует включать сечение опорного ребра и полосу стенки шириной 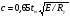 с каждой стороны ребра. Расчетную длину стойки следует принимать равной высоте стенки. с каждой стороны ребра. Расчетную длину стойки следует принимать равной высоте стенки.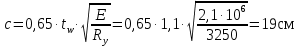 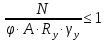 φ –коэффициент продольного изгиба. (Приложение Д-1, [1]) А=Ар+с·tw=35,2+19·1,1=56,1см2 Определим геометрические характеристики сечения: 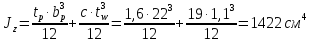 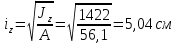 Определим гибкость опорного ребра: Определим гибкость опорного ребра: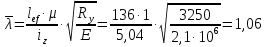 Тип сечения – С. По приложению Д-1 найдем значение φ=0,894. 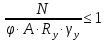 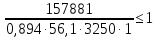 0,97≤1. Устойчивость опорного ребра обеспечена. |
