Караваев ТАУ 2019. Введение Описание принципиальной схем
 Скачать 0.87 Mb. Скачать 0.87 Mb.
|
1 2  Содержание Введение………………………………………………………………………...….3 1 Описание принципиальной схем……………………………….……..………4 2 Структурная схема и коэффициент усиления САР……………………....…5 2.1 Составление структурной схемы САР……….………………...…..…5 2.2 Определение коэффициента усиления САР…………………….....5 2.3 Определение пер-ого коэффициента динамического звена..……6 3 Передаточные функции динамических звеньев…………………………….7 3.1 Элемент сравнения……………………….……….……………......…7 3.2 Электронный усилитель………………………………………......…7 3.3 Генератор постоянного тока независимого возбуждения……..…8 3.4 Двигатель постоянного тока независимого возбуждения ……….9 3.5 Пассивное индуктивное звено…….………...…………….....….....12 3.6 Тахогенератор………………...……………….…………………...…12 3.7 Итоговые передаточные функции всех динамических звеньев.13 4 Построение частотных характеристик звеньев………………………..…..14 4.1 Построение АЧХ, ФЧХ и АФЧХ для инерционного форсирующего звена...……………………...………………..……………………….........……14 5 Передаточные функции САР…………………..……………..…..…………..15 5.1 Функциональная схема САР…………………………………….…15 5.2 Определим передаточную функцию САР…………………...……15 6 Анализ устойчивости САР методом Гурвица….....………………....……18 6.1 Анализ устойчивости САР методом Д-разбиения…..……...……19 7 Построение кривой переходного процесса…………………………..….......20 7.1 Построение вещественной частотной характеристики САР….….……23 7.2 Построение кривой переходного процесса………….…………...……..…25 7.3 Оценка качества регулирования………………...………….…………..…27 Заключение ………………………………………………………..……….….…28 Список используемой литературы…………………………...……………..…29 ВВЕДЕНИЕ В данном курсовом проекте необходимо рассчитать систему автоматического регулирования числа оборотов тягового двигателя при обточке колесных пар без выкатки. Приведенная в расчетах САР осуществляет регулирование по замкнутому циклу, система такого цикла показывает взаимосвязь между регулируемой величиной и управляющим воздействием при равенстве нулю возмущающих воздействий, так же для данной системы характерно наличие ошибки регулирования, такие системы называют статическими. Замкнутая система способна скомпенсировать как внешние возмущения, так и отклонения характеристик собственных элементов. 1 Описание принципиальной схемы На рисунке 1.1 изображена САР числа оборотов тягового двигателя при обточке колесных пар без выкатки.  Рисунок 1.1 - САР числа оборотов тягового двигателя при обточке колесных пар без выкатки Величина напряжения на входе электронного усилителя будет определяться разностью заданного напряжения  и напряжения тахогенератора и напряжения тахогенератора  : : (1.1) (1.1)При обточке обороты понижаются 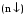 , следовательно напряжение на тахогенераторе падает , следовательно напряжение на тахогенераторе падает  , что приводит к возрастанию , что приводит к возрастанию  ,значит напряжение динамического звена повышается ,значит напряжение динамического звена повышается  , следовательно напряжение электронного усилителя повышается , следовательно напряжение электронного усилителя повышается  и напряжение генератора тоже повышается и напряжение генератора тоже повышается  и обороты увеличиваются и обороты увеличиваются  . .Напряжение динамического звена понижается 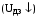 , напряжение электрического усилителя понижается , напряжение электрического усилителя понижается 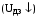 2 Структурная схема сар и определение коэффициента усиления 2.1 Составление структурной схемы САР На рисунке 2.1 изображена структурная схема САР  Рисунок 2.1 - Структурная схема САР Элемент сравнения (ЭС) – производит сравнение заданного напряжения  , с напряжением тахогенератора , с напряжением тахогенератора  . .Динамическое звено (ДЗ) – делит входное напряжение. Электронный усилитель (ЭУ) – усиливает сигнал рассогласования до необходимого значения. Обмотка возбуждения генератора (ОВ) – обеспечивает необходимое возбуждение генератора. Якорь генератора (Г) – вырабатывает регулирующее воздействие. Якорь двигателя (Д) – вращает рабочий механизм. 2.2 Определение коэффициента усиления САР Величина необходимого коэффициента усиления системы находится из условия обеспечения в замкнутой системе заданной статической ошибки регулирования:  где  - статистическая ошибка замкнутой системы (см. бланк задания); - статистическая ошибка замкнутой системы (см. бланк задания);  ‑ статистическая ошибка разомкнутой системы при приложении к ней возмущающего воздействия (см. бланк задания); K - коэффициент усиления САР. ‑ статистическая ошибка разомкнутой системы при приложении к ней возмущающего воздействия (см. бланк задания); K - коэффициент усиления САР.Задавшись статистическими ошибками замкнутой и разомкнутой САР из (3.1) можно получить необходимый коэффициент усиления системы, он будет равен:  Подставив все известные значения в формулу 3.2 получим K=(12/1,3)–1=8,23. 2.3 Определение передаточного коэффициента динамического звена Коэффициент передачи электронного усилителя можно найти из следующего выражения:  (2.3) (2.3)Подставив все известные значения в формулу 2.3 получим  3 Передаточные функции динамических звеньев 3.1 Элемент сравнения В рассматриваемом примере рисунке 2.1 в качестве элемента сравнения используется схема вычисления двух напряжений. Уравнение, описывающее связь входного напряжения усилителя с задающим напряжением и напряжением цепи обратной связи, имеет следующий вид:  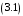 При расчетах систем автоматической стабилизации работающих по замкнутому циклу считается, что элемент сравнения идеален, т. е. не вносит погрешность в процесс регулирования. 3.2 Электронный усилитель Так как электронные усилители обычно имеют очень малую инерционность, то ее величиной можно пренебречь. Электронный усилитель считая усилитель безынерционным звеном. В результате имеем простейшее уравнение для описания его работы:  (3.2) (3.2)где 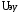 - напряжение на выходе усилителя; - напряжение на выходе усилителя;  – коэффициент передачи электронного усилителя; – коэффициент передачи электронного усилителя;  - напряжение на входе электронного усилителя. - напряжение на входе электронного усилителя. (3.3) (3.3) где p-оператор Лапласа.   3.3 Генератор постоянного тока независимого возбуждения Обмотка возбуждения. Дифференциальное уравнение на основании второго закона Кирхгофа для цепи возбуждения генератора имеет вид:  , (3.4) , (3.4)где  – индуктивность обмотки возбуждения; – индуктивность обмотки возбуждения;  – ток в обмотке возбуждения (выходная величина); – ток в обмотке возбуждения (выходная величина);  – активное сопротивление обмотки возбуждения; – активное сопротивление обмотки возбуждения;  – напряжение на обмотке возбуждения (входная величина). – напряжение на обмотке возбуждения (входная величина).Разделим уравнение на произведение  , в результате получим: , в результате получим: (3.5) (3.5)Выполним сокращения и перейдем к операторной форме записи: 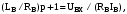 (3.6) (3.6)где p – оператор Лапласа. Умножим обе части выражения на  и приведем уравнение к стандартному виду: и приведем уравнение к стандартному виду: (3.7) (3.7)Передаточная функция обмотки возбуждения, как апериодического звена первого порядка, имеет вид:  (3.8) (3.8)Исходя из условий варианта имеем:  Якорь генератора. На основании метода графической линеаризации имеем линеаризованное уравнение:  (3.9) (3.9)где  - напряжение на зажимах якоря генератора (выходная величина); tg ‑ угол наклона касательной к характеристике генератора в рабочей точке; - напряжение на зажимах якоря генератора (выходная величина); tg ‑ угол наклона касательной к характеристике генератора в рабочей точке;  ‑ коэффициент передачи якоря генератора. ‑ коэффициент передачи якоря генератора.Передаточная функция якоря генератора как безынерционного звена будет иметь вид:  (3.10) (3.10) Перемножая передаточные функции обмотки возбуждения и якоря генератора, получим передаточную функцию генератора  : :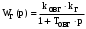 . (3.11) . (3.11)Подставим известные численные значения получим:  . .3.4 Двигатель постоянного тока независимого возбуждения На основании записи второго закона Кирхгофа для цепи якоря:  (3.12) (3.12)где  – индуктивность обмотки якоря; – индуктивность обмотки якоря; 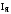 – ток в обмотке якоря; – ток в обмотке якоря;  – активное сопротивление обмотки якоря; n – обороты вала двигателя (выходная величина); Ф – магнитный поток обмотки возбуждения (Ф = const); – активное сопротивление обмотки якоря; n – обороты вала двигателя (выходная величина); Ф – магнитный поток обмотки возбуждения (Ф = const);  – напряжение на обмотке якоря (входная величина); – напряжение на обмотке якоря (входная величина);  – коэффициент пропорциональности. – коэффициент пропорциональности.На основании закона равновесия моментов на валу якоря, оно имеет вид:  (3.13) (3.13)где  – коэффициент пропорциональности; J – приведенный момент инерции вала двигателя; M – момент сопротивления на валу якоря. – коэффициент пропорциональности; J – приведенный момент инерции вала двигателя; M – момент сопротивления на валу якоря.Для приращений переменных параметров с учетом малых отклонений при условии постоянства магнитного потока можно записать следующую систему уравнений:  (3.14) (3.14) Из второго уравнения системы имеем:  (3.15) (3.15)Подставляем выражение (3.12) в первое уравнение системы (3.11) и переходим к операторной форме записи, в результате чего получим: 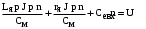 . (3.16) . (3.16)Разделим обе части уравнения на Cе и перегруппируем слагаемые:  . (3.17) . (3.17)Вводим новые обозначения и переходим к стандартной форме записи дифференциального уравнения:  (3.18) (3.18)где  – постоянная времени цепи якоря – постоянная времени цепи якоря   – электромеханическая постоянная времени двигателя – электромеханическая постоянная времени двигателя   – коэффициент передачи двигателя – коэффициент передачи двигателя  Передаточная функция двигателя независимого возбуждения, как апериодического звена второго порядка, имеет вид:  (3.19) (3.19)или  (3.20) (3.20)где T3,4 – новые постоянные времени двигателя, определяемые по выражению:  (3.21) (3.21)Вычислим  : : , , . .Подставим в (3.20) заданные значения  3.5 Пассивное индуктивное звено Представив пассивное интегрирующие звено в виде делителя напряжения получим передаточную функцию:  (3.22) (3.22)где  – полное сопротивление второго (выходного) плеча делителя; – полное сопротивление второго (выходного) плеча делителя;  полное сопротивление первого плеча делителя. pL – операторная форма записи полного сопротивления на индуктивности L. полное сопротивление первого плеча делителя. pL – операторная форма записи полного сопротивления на индуктивности L.Подставим  и и  и разделим слагаемые в числителе и знаменателе выражения передаточной функции (3.22) на и разделим слагаемые в числителе и знаменателе выражения передаточной функции (3.22) на  получим: получим: . (3.23) . (3.23)Введем коэффициент передачи  и постоянную времени и постоянную времени  В итоге получим передаточную функцию пассивного индуктивного звена, как апериодического звена первого порядка: В итоге получим передаточную функцию пассивного индуктивного звена, как апериодического звена первого порядка: . (3.24) . (3.24)В численном виде получим:  . .3.6 Тахогенератор Уравнение описывающее работу тахогенератора имеет вид:  (3.25) (3.25)где  – напряжение на зажимах тахогенератора (выходная величина); – напряжение на зажимах тахогенератора (выходная величина); 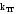 ‑ коэффициент передачи тахогенератора; n – обороты вала (входная величина). ‑ коэффициент передачи тахогенератора; n – обороты вала (входная величина).Передаточная функция тахогенератора как безынерционного звена будет иметь вид: 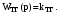 (3.26) (3.26)В численном виде будем иметь:  3.7 Итоговые передаточные функции всех динамических звеньев  4 Построение частотных характеристик звеньев 4.1 Построение АЧХ, ФЧХ и АФЧХ для инерционного форсирующего звена Имеем следующую передаточную функцию: 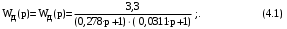 Из передаточной функции получим АЧХ следующего вида  Из передаточной функции получим ФЧХ следующего вида  Для расчета АЧХ ФЧХ и АФЧХ используется программа maple которая изображена на рисунке 4.1  Рисунок 4.1 - Программа maple АЧХ ФЧХ АФЧХ График АЧХ представлен на рисунке 4.2  Рисунок 4.2 - АЧХ двигателя График ФЧХ представлен на рисунке 4.3 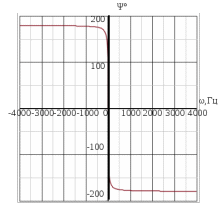 Рисунок 4.3 - ФЧХ двигателя График АФЧХ представлен на рисунке 4.4  Рисунок 4.4 - АФЧХ двигателя 5 ПЕРЕДАТОЧНЫЕ ФУНКЦИИ САР 5.1 Функциональная схема САР Функциональная схема САР изображена на рисунке 5.1  Рисунок 5.1 - Функциональная схема САР 5.2 Определим передаточную функцию САР Передаточная функция разомкнутой системы равна отношению регулируемой величины к ошибке регулирования при равенстве нулю возмущающих воздействий. Размыкание можно сделать в любой точке системы. Так как данная схема представляет собой простую цепь с последовательным соединением динамических звеньев, то передаточная функция разомкнутой системы будет равна произведению передаточных функций отдельных звеньев. Передаточная функция разомкнутой цепи имеет следующий вид:  (5.1) (5.1)5.3 Передаточная функция замкнутой системы Передаточная функция замкнутой системы показывает взаимосвязь между регулируемой величиной и управляющим воздействием при равенстве нулю ре- гулируемой величиной и управляющим воздействием при равенстве нулю возмущающих воздействий. Выражение для передаточной функции замкнутой системы может быть найдено по известной передаточной функции разомкнутой системы следующим образом:  , (5.2) , (5.2)где  – передаточная функция замкнутой системы. – передаточная функция замкнутой системы.Подставим выражение (5.2) в уравнение (5.3) и получим:  . (5.3) . (5.3) 1 2 |
