Караваев ТАУ 2019. Введение Описание принципиальной схем
 Скачать 0.87 Mb.
|
1 2 5.4 Характеристическое уравнение системыХарактеристическое уравнение системы есть знаменатель операторного выражения передаточной функции замкнутой системы: 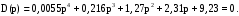 (5.4)6 АНАЛИЗ УСТОЙЧИВОСТИ САР МЕТОДОМ ГУРВИЦА Передаточная функция разомкнутой САР имеет следующий вид 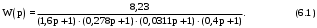 Передаточная функция замкнутой САР имеет следующий вид 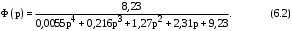 По характеристическому уравнению составляют квадратную матрицу коэффициентов, содержащую n строк и n столбцов, где n – показатель степени полинома характеристического уравнения. 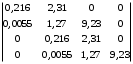 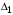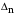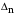После построения матрицы из нее выделяют определители Гурвица (диагональные миноры)  …  , их число равно n, последний определитель включает в себя всю матрицу. Вывод: Для устойчивости САР необходимо и достаточно что бы при положительности коэффициента при старшей степени были больше нуля все n квадратичные определители матрицы Гурвица. Исходя из полученных результатов можно сделать вывод, что система устойчива. 6.2 Анализ устойчивости САР методом Д-разбиения Программа maple для анализа устойчивости САП приведена на рисунке 6.1 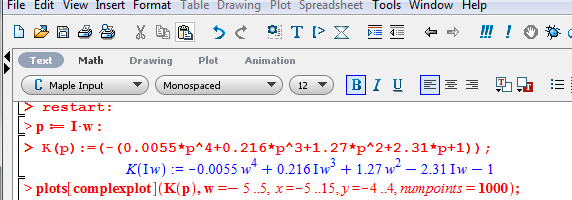 Рисунок 6.1 – Программа maple На рисунке 6.2 представлен График, полученный при использовании метода Д-разбиения 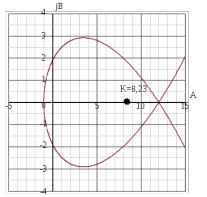 Рисунок 6.2 - Область устойчивости Вывод: САР является устойчивой так как на полученном графике 6.2 коэффициент К входит в диапазон устойчивости от -1 до +12. 7 ПОСТРОЕНИЕ КРИВОЙ ПЕРЕХОДНОГО ПРОЦЕССА 7.1 Построение вещественной частотной характеристики САР Выделив из передаточной функции вещественную часть, получим уравнение следующего вида 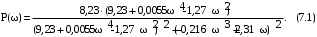 Программа maple для построения вещественной частотной характеристики САР представлена на рисунке 7.1 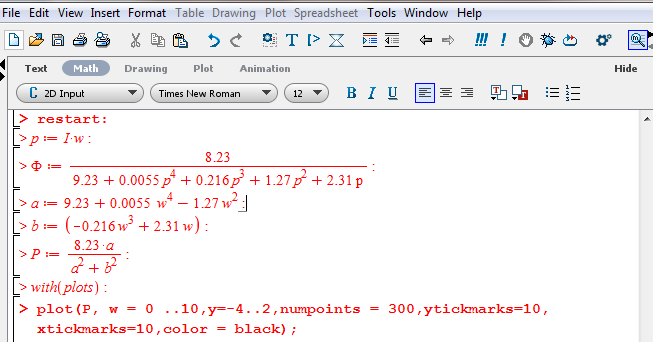 Рисунок 7.1 - Программа maple построения вещественной характеристики САР График вещественной частотной характеристики САР, полученный по результатам расчета представлен на рисунке 7.2 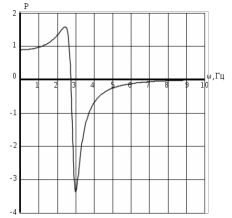 Рисунок 7.2 - Вещественная частотная характеристика САР 7.2 Построение кривой переходного процесса Вписывание трапеций представлено на рисунке 7.3 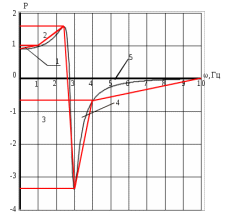 Рисунок 7.3 – Вписывание трапеций 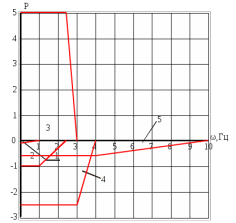 Рисунок 7.4 – Параметры трапеций Полученные параметры для всех трапеций сведем в таблицу 7.1 Таблица 7.1 - Параметры трапеций
Для всех трапеций формируются расчетные таблицы xi(t) которые приведены ниже Таблица 7.2 - Расчетные данные х1(t); x2(t); x3(t) х4(t); x5(t);
По рассчитанным данным построим кривые переходного процесса рисунок 7.5 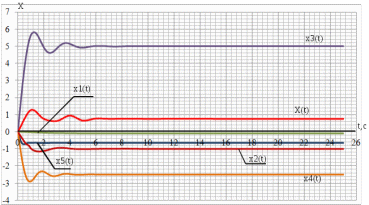 Рисунок 7.5 – Кривые переходного процесса На рисунке 7.6 изображена суммарная кривая, по которой дается оценка качества регулирования. 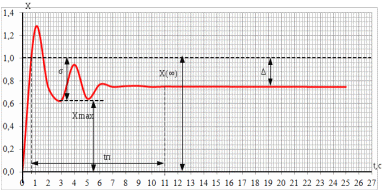 Рисунок 7.6 – Оценка качества регулирования Величина перерегулирования рассчитывается по следующей формуле: 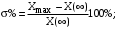 (7.6)где 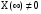 представляет собой установившееся значение регулируемой величины после завершения переходного процесса; 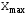 - максимальное значение регулируемой величины. 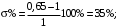Из рисунка 8.5 видно, что перерегулирование отсутствует. Сведем результаты, полученные на графике в таблицу 7.3 Таблица 7.3 - Результаты расчета оценки качества регулирования
Вывод: Оценка САР является неудовлетворительной, так как значение статической ошибки не соответствуют допускаемым значениям 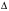 =25% при норме 2%-4%, время переходного процесса (время протекающее от момента приложения на вход единичного скачка задающего воздействия до момента, после которого регулируемая величина достигла заданного значения в пределах допустимой ошибки) составляет 10,4 с. Перерегулирование является также неудовлетворительным и составляет  = 35% при норме до 30% .Заключение В данном курсовом проекте был произведен расчет САР регулирования числа оборотов тягового двигателя при обточке колесных пар без выкатки. Также были описаны передаточные функции всех динамических звеньев САР. При заданных параметрах, по результатам расчетов можно сделать вывод, что система является устойчивой по критерию устойчивости Гурвица так как для устойчивости САР необходимо и достаточно что бы при положительности коэффициента при старшей степени были больше нуля все n квадратичные определители матрицы Гурвица, а из полученных нами результатов можно сделать вывод, что система устойчива. Анализ устойчивости САР Методом Д-разбиения также показал что система устойчива, по результатам расчета качества САР можно сделать вывод, что САР имеет негативную оценку качества и требует доработки. Список используемых источников 1 Теория систем автоматического управления : метод. указания для выполнения курсового проекта / С.В. Доронин. – Хабаровск: Изд-во ДВГУПС, 2015. – 49 с. : ил. 2 Дробот Ю.Б. Введение в пакет Maple V: Монография. - Хабаровск: Изд-во ДВГУПС, 1999-244 с. – ил. Лист     Изм Лист № документа Подпись Дата КП 23.05.03.19 1 ПЗ 1 2 |
