Методы расчетов кз. Реферат. Методы расчётов предельных по статической устойчивости. Введение понятие о статической устойчивости

• Название: Введение понятие о статической устойчивости
• Анкор: Методы расчетов кз
• Дата: 13.02.2023
• Размер: 1.28 Mb.
• Имя файла: Реферат. Методы расчётов предельных по статической устойчивости .doc
• Тип: Реферат; #934935

СОДЕРЖАНИЕ
Введение …………………………………………………………….3

1. Понятие о статической устойчивости……………………………..10

2. Анализ методов экспресс-расчетов предельных режимов……….12

2.1. Метод дискретного утяжеления………………………………...15

2.2. Метод непрерывного утяжеления ……………………………...18

2.3. Применение уравнений предельных режимов для

определения параметров X_пр, Y_пр……………………………….23

2.4. Построение областей устойчивости…………………………….26

Заключение…………………………………………………………..28

Библиографический список………………………………………...30

ВВЕДЕНИЕ
Расчеты установившихся режимов (УР) являются основными при решении задач, связанных с проектированием и эксплуатацией электрических систем (ЭС). Результаты этих расчетов используются при планировании режимов и оперативном управлении ЭС, а также служат базой для выполнения оптимизации, анализа устойчивости и надежности [1..10].

В настоящее время актуальность задач расчета установившихся режимов возросла вследствие создания автоматизированных систем диспетчерского и противоаварийного управления на базе ЭВМ.

Появились также новые задачи, связанные с определением пределов и запасов статической устойчивости. Необходимость решения этих задач непосредственно в цикле управления ЭС на основе информации, получаемой по каналам телемеханики, потребовала разработки новых методов расчета УР в реальном масштабе времени.

Исходную информацию, необходимую для расчета установившегося режима ЭС, можно разделить на три группы.

В первую входят параметры схемы замещения, к которым относятся: сопротивления линий электропередачи (ЛЭП), коэффициенты трансформации, шунты намагничивания и сопротивления трансформаторов, емкостные проводимости ЛЭП и индуктивные реакторов. Указанные элементы энергосистемы связывают в единую схему путем задания информации о топологии ЭС.

Вторую группу образуют данные о нагрузках ЭС, которые могут задаваться в виде эквивалентных шунтов, постоянных отборов мощности, статических характеристик, зависящих от напряжения и частоты.

Третья группа информации складывается из данных об источниках электроэнергии: активных мощностей P и модулей U напряжений синхронных генераторов (СГ), снабженных автоматическими регуляторами возбуждения (АРВ); реактивных мощностей Q СГ, не имеющих АРВ; статизмов  результатов скорости первичных двигателей и т.д.

В результате расчета УР определяются модули U_i и фазы _i напряжений в узлах сети, перетоки (P_ij, Q_ij) и потери (P_ij, Q_ij) активных и реактивных мощностей, токи Iij в ЛЭП, частоты f в системе. В общем виде процесс преобразования информации при расчете установившегося режима можно представить в виде рис.1.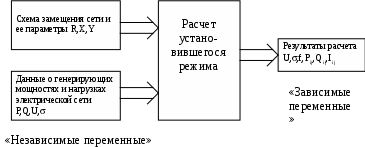




Рис.1. Процесс преобразования информации об ЭС

при расчете установившегося режима

Данные о генерирующих мощностях и нагрузках называются независимыми переменными. Результаты же расчета являются зависимыми переменными.

В задании любой независимой переменной, как правило, имеет место погрешность. Это приводит к некоторой неопределенности результатов расчета. Величина погрешности сильно зависит от того, насколько далеко вперед прогнозируется схемно-режимные ситуации в ЭС.

В автоматизированных системах диспетчерского управления (АСДУ) решаемые задачи делятся по временному принципу. Так на стадии долгосрочного планирования расчеты выполняются на год, месяц или неделю, при краткосрочном планировании оценивают схемно-режимные ситуации на следующие сутки. В процессе оперативного управления наряду с оценкой текущей ситуации делается прогноз на час или несколько часов вперед. Естественно, чем дальше вперед делается прогноз, тем менее точно определяется потокораспределение.

Элемент неопределенности, конечно, является весьма нежелательным фактором при расчетах. Но, к сожалению, погрешности задания независимых переменных параметров можно уменьшить, но нельзя полностью устранить.

Рассмотрим, например, данные о сопротивлении ЛЭП. В СССР погрешность их задания составляет около 5%. Это связано не столько с отсутствием более достоверных данных, но и с тем, что сопротивление изменяется в зависимости от погодных условий, протекающего по электропередаче тока и др. Существенно влияет на результаты расчетов УР и погрешность в задании коэффициентов трансформации. В настоящее время информация о текущих значениях параметров режима собирается в различных точках энергосистемы и передается в диспетчерские центры с помощью телемеханических устройств. Эта информация, тем не менее, не является абсолютно достоверной, т.к. является неполной (охватить всю энергосистему телеизмерениями нельзя по экономическим соображениям), содержит погрешности, обусловленные измерительными приборами и разновременностью измерений, может содержать грубые ошибки, связанные с отказами датчиков и каналов передачи информации. За счет избыточного количества измерений в некоторых районах энергосистемы обычно удается значительно повысить достоверность данных о текущем режиме ЭС. Это делается с помощью специальных алгоритмов оценивания состояния. Однако элемент неопределенности здесь все же остается.

Как уже упоминалось, неопределенность определения независимых переменных резко возрастает при попытке анализа будущих состояний энергосистемы (при оперативном управлении, краткосрочном и долгосрочном планировании). Наибольшие затруднения при этом вызывает необходимость прогнозирования нагрузок ЭС. В настоящее время существует методический аппарат прогноза нагрузок, который опирается на выявление регулярной составляющей их изменения в течение суток, по дням недели, месяцам, кварталам и годам. Затем соответствующие статистические данные используются для экстраполяции на будущее. Однако нагрузка ЭС подвержена также и нерегулируемым колебаниям, что, естественно, невозможно учесть. Это вызывает расхождение планируемых и действительных режимов энергосистем.

В связи с наличием фактора неопределенности появились работы, в которых предлагается перейти от детерминированной постановки задачи к вероятностной. При таком подходе входные и выходные данные рассматриваются как случайные величины с известными математическими ожиданиями и дисперсиями. В результате расчета определяется «наиболее вероятное» значение зависимых переменных и возможный разброс относительного этого значения. Однако практического применения этот подход пока не получил. В математическом отношении задача расчета установившегося режима сводится к решению больших систем нелинейных уравнений. Нелинейный характер задачи обуславливается следующими причинами:

• 
  нелинейной зависимостью токов генераторов и нагрузок от напряжения;
  
• 
  нелинейной зависимостью мощностей генераторов и проводимостей от частоты.
  

Сказанное определяет ряд специфических свойств задачи. Во-первых, решения существуют не для всех значений мощностей генераторов и нагрузок в узлах сети. Во-вторых, каждому сочетанию узловых мощностей при существовании режима может соответствовать множество решений.

Решение системы нелинейных уравнений установившегося режима возможно только приближенными, итерационными методами. При этом весьма важным является надежность получения решения, если оно существует. С другой стороны, учитывая большую размерность задачи, весьма острым требованием является быстродействие итерационных процедур. Эти требования находятся в противоречии друг с другом, и любой из много численных методов расчета потокораспределения является компромиссным с точки зрения надежности или быстродействия.

Другая особенность состоит в том, что учет ограничений на параметры режима (например, на диапазоны изменения реактивных мощностей генераторов) приводит к необходимости замены некоторых уравнений системы в ходе самого расчета. Это порождает дополнительное множество альтернативных решений и усложняет сходимость итерационных процедур [11].

Современные энергосистемы (ЭС) характеризуются концентрацией значительных мощностей на отдельных станциях, объединенных на параллельную работу линиями электропередачи большой протяженности. Сложность схем и многообразие режимов работы ЭС приводит к необходимости применения непосредственно в цикле оперативного управления энергосистемами развитых средств информационной и вычислительной техники [12, 13, 14, 15, 16, 17, 18, 19, 20] .

Одна из важнейших задач оперативного управления ЭС состоит в обеспечении статической устойчивости (СУ) нормальных и, особенно, послеаварийных режимов [21, 22]. Именно ограничения по статической устойчивости определяют, в основном, допустимую область управления режимами. Проблема анализа СУ возникает и в практике проектирования энергосистем, а также при настройке устройств автоматического регулирования для отдельных элементов ЭС. Поэтому от корректности расчетов СУ и принимаемых на основе их результатов решений непосредственно зависят как уровень надежности работы энергосистем, так и полнота использования пропускной способности электрических сетей.

Основой для анализа устойчивости являются результаты расчетов предельных по СУ режимов. Для повышения эффективности расчетов предельных режимов (ПР) требуется создание математических моделей и методов, достаточно полно учитывающих специфику уравнений, описывающих установившиеся режимы.

Проблема расчетов установившихся режимов для задач проектирования, краткосрочного и долгосрочного планирования в сложных ЭС, содержащих сотни и тысячи узлов, в основном решена. Существующее программное обеспечение, благодаря широкому применению современных методов учета слабой заполненности матриц [23], обеспечивает достаточное для указанного класса задач быстродействие.

Применение корректирующих коэффициентов в методе Ньютона, а также использование алгоритмов, учитывающих нелинейные члены разложения функций невязок в ряд Тейлора [14], позволило решить проблему надежной сходимости итерационных процессов при расчете «тяжелых» режимов, близких к предельным по устойчивости [24] . В результате расчеты режимов по базовым схемам ЭС, содержащим более тысячи узлов, происходят за минуты, а по оперативным схемам, включающим несколько сотен узлов – за десятки секунд [25] .

Однако в настоящее время все более актуальными становятся задачи, связанные с расчетом предельных режимов и оценкой запасов СУ непосредственно в цикле оперативного управления ЭС. Это приводит к необходимости разработки эффективных методов и алгоритмов, обеспечивающих как высокое быстродействие, так и надежность получения результата. Это вызвано тем, что при оперативном управлении расчеты ПР должны проводится в темпе процесса изменения схемно-режимной ситуации, а адекватная работа централизованных систем противоаварийной автоматики (ПАА) требует просмотра большого количества аварийных ситуаций за весьма короткое время, обусловленное значительной скоростью изменения параметров режима. Поэтому требуется разработка новых подходов, более полно учитывающих специфику задач оперативного управления.

1. Понятие о статической устойчивости
Под статической устойчивостью электрической системы понимается ее способность восстанавливать исходный режим, характеризующийся параметрами 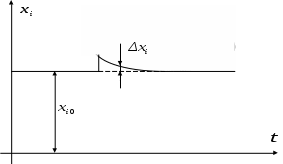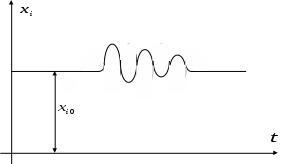, после кратковременного воздействия малого возмущения (рис. 2). В Качестве параметров Х обычно принимают напряжение в узловых точках и токи в ветвях ЭС, а под понимают изменение механического момента на валу двигателя одного из генераторов или мощности нагрузки. Вследствие малости рассматриваемых возмущений, ЭС при анализе статической устойчивости может рассматриваться как линейная динамическая система [26] .






Рис. 2. Характер переходных процессов в статически

устойчивой ЭС
Нарушение статической устойчивости может происходить вследствие причин различной физической природы. Например, если мощность турбины достигнет максимально возможного (предельного) значения электромагнитной мощности генератора, происходит апериодическое нарушение устойчивости; при работе генератора на холостом ходу или с малой нагрузкой через ЛЭП, обладающую значительным активным сопротивлением, возможно самораскачивание, проявляющееся в виде нарастающих колебаний угла . Аналогичное явление происходит при неправильной настройке автоматического регулятора возбуждения (АРВ).

2. 
   Анализ методов экспресс-расчетов
   

предельных режимов
Достигнутые за последние годы успехи в создании алгоритмов и программ расчета предельных режимов объясняются не только совершенствованием вычислительной техники, но, в большей степени, интенсивным развитием численных методов решения УУР.

Уравнения установившегося режима ЭС можно записать в виде:
(1)
где F- нелинейная вектор-функция; - вектор нерегулируемых параметров режима (зависимых переменных); - вектор регулируемых параметров режима(независимых переменных).

Предельные по статической апериодической устойчивости режимы определяются уравнениями (1) и условием

(2)

где матрица, отвечающая свободному члену характеристического полинома

(3)

системы дифференциальных уравнений

(4)

описывающих переходные процессы в ЭС при малых возмущениях. Одновременно является матрицей Якоби УУР.

Правые части дифференциальных уравнений являются функциями невязок УУР, которые обращаются в нуль в точках равновесия. Для исследования предельных режимов используется метод малых колебаний. Суть метода заключается в замене нелинейных дифференциальных уравнений (4) линеаризованными:

(5)
где - параметры исследуемого на устойчивость режима работы ЭС, удовлетворяющие системе уравнений (1).

Процедура линеаризации выполняется на основе разложения функций 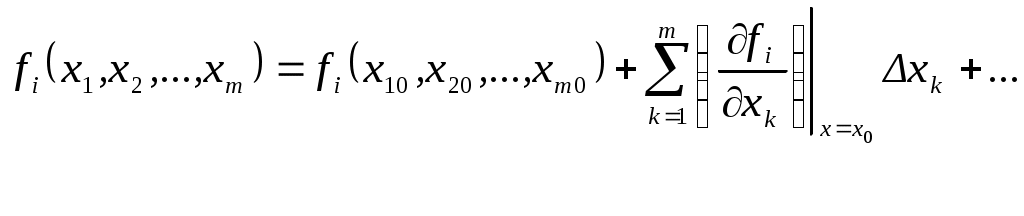в ряд Тейлора:



и отбрасывания нелинейных членов разложения. Тогда

(6)

Согласно первой теореме Ляпунова, положение равновесия системы УУР будет асимптотически устойчивым, если все корни характеристического уравнения (3) линеаризованной системы будут иметь отрицательные действительные части.

Так для ЭС практически всегда выполняется условие .

то изменение знака свободного члена характеристического уравнения (3) по сравнению с исходным, заведомо устойчивым режимом означает, что стал положительным один из действительных корней. Поэтому равенство (2) определяет границу апериодической устойчивости и кроме того границу существования решения уравнений (1).

Предельным режимам ЭС отвечают параметры , удовлетворяющие уравнениям (1) и условию (2). Точки образуют в пространстве Y гиперповерхность .

2.1. Метод дискретного утяжеления
Традиционные методы расчета предельных режимов основаны на дискретном утяжелении исходного стационарного режима по какому-либо параметру или группе параметров. Расчет содержит следующие этапы:

1. Находится вектор переменных исходного, заведомо устойчивого режима путем решения уравнений



2. При найденном рассчитывается величина



и фиксируется ее знак, который зависит от последовательности написания уравнений и может быть любым.

3. Задается нормированный вектор , определяющий направление утяжеления в пространстве регулируемых параметров Y (см. рис. 3).

Длина вектора :

.

4. Решается уравнение



и определяются параметры утяжеленного режима. При этом

,

где Т₁ – соответсвует первой ступени утяжеления.

5. При найденных значениях 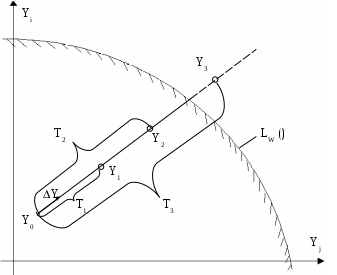вычисляется величина .



Рис. 3. Утяжеление режима.
Утяжеление продолжается до тех пор, пока на k-том шаге

, T_k=k*T₁

не произойдет изменение знака (точка Y окажется между границами L_W ( ) и L_F ( )) или пока решение уравнений



не перестанет существовать.

Последнее свидетельствует о том, что режим, предельный по передаваемой мощности, наступает раньше предельного по устойчивости [27].

Начальный шаг утяжеления выбирается достаточно большим, а после первого пересечения поверхности L_W происходит его деление пополам. Процесс дробления заканчивается после того, как длина шага останется меньше заданной точности по иска параметров Y_пр.
Для определения предельного режима методом дискретного утяжеления с достаточной точностью, длина шага утяжеления должна быть невелика. Это приводит к необходимости расчета большого числа промежуточных режимов, как правило, не интересующих расчетчика. Для сокращения вычислений и повышения точности поиска параметров предельного режима прибегают к процедуре дробления шага.

Расчет последовательно утяжеляемых режимов, требующий больших затрат времени необходим потому, что якобиан уравнений установившегося режима не представим в виде аналитических выражений и может быть получен только численно. Кроме того, в искомой точке предельного режима матрица Якоби УУР становится вырожденной и возникают существенные трудности, вызванные необходимостью решения плохо обусловленных систем линейных уравнений (СЛУ)[13].

Кроме того, сложность возникает и при выборе начального шага утяжеления. Малая величина приводит к затягиванию процесса вычислений. Слишком большой шаг приводит к большому количеству расходящихся промежуточных режимов, что также увеличивает время счета.

При наличии ограничений по реактивной мощности генераторов, поиск параметров X_пр, Y_пр становится невозможным без применения специальных приемов.

К преимуществам методов дискретного утяжеления можно отнести простоту реализации, возможность изменения параметров режима на любом шаге утяжеления. Это дает возможность учитывать ограничения-неравенства.

2.2. Методы непрерывного утяжеления
Для определения предельных режимов в работе [28] был предложен способ непрерывного утяжеления, основанный на использовании одной из модификаций метода Ньютона.

В основе метода Ньютона лежит линеаризация решаемых уравнений в точке текущего приближения. Разложим вектор-функцию УРР F(X, Y) при заланном Y в ряд Тейлора и отбросим нелинейные члены:

(7)

Решить уравнения

F(X)=0,

значит найти такую точку X^(K+1), в которой F[X^(K+1)] обращается в нуль. Поэтому, приравнивая левую часть в разложении (7) нулю, получим итерационную формулу для метода Ньютона:

(8)

Применение в этой процедуре обратной матрицы Якоби УРР не означает, что ее необходимо получать на каждой итерации в явном виде. Действительно, перепишем (8) в следующем виде

; (9)

, (10)

где X^(k) – вектор поправок.

Вычисление X^(k) связано с решением системы линейных уравнений (10), что не требует прямого обращения матрицы Якоби.

Решение линейной системы (10) требует меньших ресурсов ЭВМ, чем обращение матрицы, поэтому в практике расчетов используется, как правило, итерационная формула (9).

В случае монотонности функции f(x) метод обеспечивает получение решения с любого приближения. Если функция немонотонная, то получение решения существенно зависит от начального приближения. Метод может «проскочить» интересующее решение и выйти к другому, или вообще разойтись.

Таким образом, обладая быстрой и надежной сходимостью вблизи решения, метод Ньютона очень чувствителен к выбору начальных приближений, что является одним из его недостатков. Второй недостаток обусловлен необходимостью решения систем линейных уравнений на каждой итерации. При использовании стандартных алгоритмов решения СЛУ требуемый объем памяти для хранения матрицы коэффициентов пропорционален квадрату, а время отсчета – кубу, числа узлов рассматриваемой электрической системы. Даже современные ЭВМ были бы не в состоянии обеспечить в этом случае расчет сложных электрических систем, содержащих сотни узлов.

По указанным причинам метод Ньютона долгое время не находил широкого применения для расчетов режимов. Только в результате разработки модификаций метода, обеспечивающих более стабильную сходимость итерационного процесса, и использования вычислительных схем СЛУ, эффективно учитывающих слабую заполненность матрицы Якоби, рассмотренные недостатки удалось преодолеть. В настоящее время метод Ньютона реализован в большом числе программ, предназначенных для расчетов режимов сложных ЭС.

Модификация метода Ньютона, использованная в работе [28] для реализации способа непрерывного утяжеления, основана на использовании итерационной процедуры вида [2]:

, (11)

где 0 < _k  1 – корректирующий коэффициент, определяющий величину шага и выбираемый на основе соотношений

1/В_k, если B_k > 1;

_k=  (12)

1, если В_k  1,
где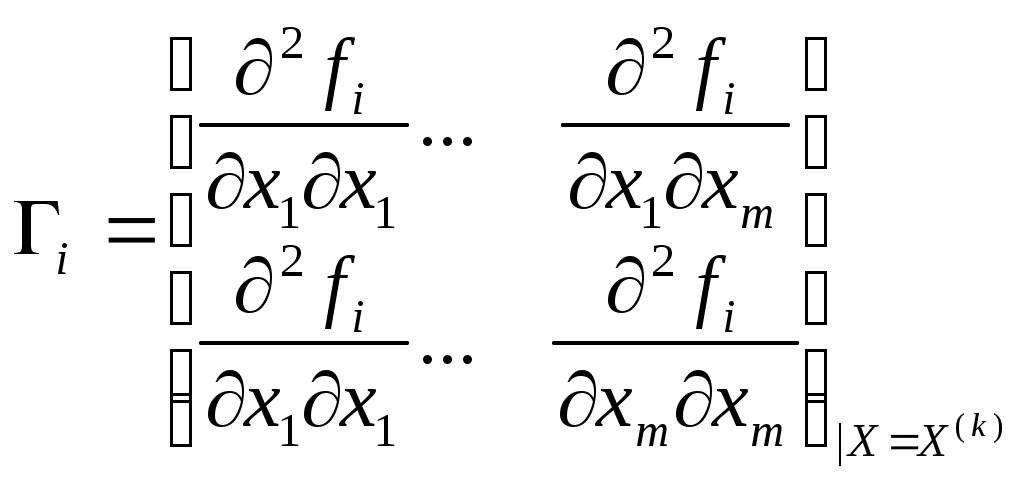



- модуль максимальной невязки;



_{- матрица Гессе от функции fi (x), вычисленная в точке X}^(k)_.

Второй сомножитель для В_k представляет собой максимальный по модулю элемент вектора, полученного в результате умножения матрицы вторых производных вектор-функции F(X) на компоненты вектора поправок X^(k). доказано, что если не происходит вырождение матрицы , итерационная процедура (11) обеспечивает сходимость вычислительного процесса для любых существующих режимов вплоть до предельных, а при расчете несуществующих режимов процесс вычислений сходится к точке предельной гиперповерхности, где Якобиан системы УРР (предполагается, что пределы передаваемой мощности и устойчивости равны, т.е. вектор-функции F(X,Y) и W(X,Y) совпадают) равен нулю.

Суть способа непрерывного утяжеления можно пояснить на ходе итерационного процесса на плоскости двух параметров Y₁ и Y₂. При этом исходному режиму соответствует точка (Y₁⁽⁰⁾, Y₂⁽⁰⁾), а утяжеление осуществляется изменением параметра Y₂, то есть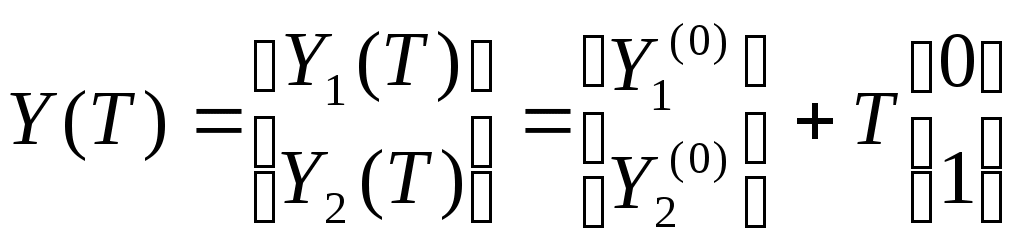



Начальная величина параметра Т выбирается таким образом, чтобы выйти за пределы области устойчивости (существования рушения). После первой итерации происходит переход в точку, где вследствие неучета нелинейных членов разложения функции F(X,Y) в ряд Тейлора, кроме невязок по утяжеляемому параметру (Y₂^(н)-Y₂⁽¹⁾) появляется невязка по другой координате (Y₁⁽¹⁾-Y₁⁽⁰⁾). По этой причине на второй итерации направление утяжеления изменяется, осуществляется переход в точку, где также имеет место отклонение от выбранной траектории Y(T), изменение направления утяжеления и т.д. При достижении предельной поверхности L_F (L_W) из-за наличия результирующих невязок по параметру Y₁, не являющемуся утяжеляемым, возникает несоответствие между полученной точкой и искомой точкой. Поэтому появляется необходимость в уточнении решения. При этом вычислительный процесс, на каждой итерации которого невязка по утяжеляемому параметру полагается нулевой, проходит вблизи предельной поверхности, где матрица плохо обусловлена.

Можно обойтись без процесса уточнения одним из следующих способов.

Первый из них основан на дополнительной балансировке неутяжеляемых параметров режима при выходе их за пределы допустимых значений.

Другой способ связан с дополнительным, по сравнению с выбранным (11) , уменьшением шага. Этим обеспечивается требуемая степень соответствия результирующей точки вычислительного процесса и искомой предельной точки.

Однако, обе рассмотренные модификации приводят к нежелательному увеличению количества итераций. Общей причиной указанных осложнений является линеаризация УУР при использовании итерационной процедуры (11). Указанный недостаток можно устранить с помощью применения вычислительных методов [14, 29], которые позволяют увеличить шаг в выбранном направлении при обеспечении заданной точности по неутяжеляемым параметрам.

Они основаны на дополнительном учете нелинейных членов разложения в ряд Тейлора вектор-функции



обратной к F(X). Благодаря этому удается обеспечить такой ход итерационного процесса, при котором невязки по параметрам, не входящим в число утяжеляемых, всегда остаются в пределах допустимых значений.

Существенным преимуществом методов непрерывного утяжеления является их быстродействие и отсутствие необходимости в выборе величины шага утяжеления. Однако при этом не снимаются вычислительные сложности, связанные с вырожденностью матрицы Якоби УУР в точке решения.

3. 
   Применение уравнений предельных режимов
   

для определения параметров X_пр, Y_пр
В работах [30, 31, 31, 33] предложено применить уравнения предельных режимов, которые дают аналитическое описание гиперповерхности предельных режимов. Существенным свойством этих уравнений является невырожденность отвечающей им матрицы Якоби в точке решения. Этим снимаются трудности с решением плохо обусловленных СЛУ.

Параметры X_пр, Y_пр. предельного по устойчивости режима могут быть найдены из решения системы нелинейных уравнений, которую можно представить в двух формах [34, 35]:

(13)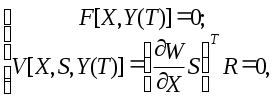

или

₍₁₄₎



где Y(T)=Y_o+T*Y – вектор регулируемых параметров, являющийся линейной функцией скалярной переменной Т;

S=[S₁ S₂ … S_i … S_m]^T – собственный вектор матрицы , отвечающий нулевому собственному значению ;

R – собственный вектор транспонированной матрицы, также отвечающий =0.

Уравнения (13) или (14), называемые уравнениями предельных режимов (УПР), получены на основе замены детерминатного равенства



эквивалентными, аналитически представимыми соотношениями

или (15)

Решение УПР каким-либо итерационным методом позволяет определить предельный по устойчивости режим в заданном направлении утяжеления. При этом снимаются трудности, связанные с необходимостью расчета серии промежуточных режимов.

В работе [34] доказано, что при совпадении пределов передаваемой мощности и устойчивости, те есть в предположении, что



матрица Якоби УПР

или

не вырождена в точках решения Х_пр. Поэтому снимаются и трудности, связанные с решением плохо обусловленных систем линейных уравнений.

Кроме того, метод определения параметров X_пр, Y_пр, основанный на использовании УПР, в отличие от методов непрерывного утяжеления, применим как при совпадении пределов устойчивости, так и при их отличии.

Из-за введения дополнительных переменных S (R) размерность УПР по сравнению с уравнениями установившегося режима повышена. Однако, как показано в работе [36], указанные переменные имеют определенный физический смысл и позволяют получить дополнительную информацию о характеристиках предельного режима.

2.4. Построение областей устойчивости
На основе соотношений (15) может быть реализована методика определения параметров X_пр, Y_пр [37, 38], применимая для построения границ областей устойчивости, а также для выбора начальных приближений при определении запасов устойчивости.

Суть методики заключается в непосредственном использовании соотношений

(16)

или

(17)

для определения точек Х_пр, принадлежащих поверхности L_W.

Рассмотрим, в качестве примера, систему (16). Задавшись вектором S=S₁ из решения уравнений

V (X, S₁) = 0

можно найти соответствующие значения Х_пр⁽¹⁾. Поворот S в положение S₂ обеспечивает определение следующей точки Х_пр⁽²⁾ (рис. 4).





Рис. 4. К определению L_W.
Таким образом, путем вращения S можно «обойти» всю предельную поверхность. Аналогично можно использовать систему (17).

По найденным значениям Х_пр из УУР можно найти соответствующие значения параметров Y_пр и построить границу L_W в координатах Y.
ЗАКЛЮЧЕНИЕ
Все более актуальными становятся задачи, связанные с расчетом предельных режимов и оценкой запасов СУ непосредственно в цикле оперативного управления ЭС. Это приводит к необходимости разработки эффективных методов и алгоритмов, обеспечивающих как высокое быстродействие, так и надежность получения результата.

При оперативном управлении расчеты предельных режимов должны проводится в темпе процесса изменения схемно-режимной ситуации, а адекватная работа централизованных систем противоаварийной автоматики требует просмотра большого количества аварийных ситуаций за весьма короткое время, обусловленное значительной скоростью изменения параметров режима. Поэтому требуется разработка новых подходов, более полно учитывающих специфику задач оперативного управления.

На основе рассмотренного в данной работе материала существующие методы расчетов предельных по статической устойчивости режимов энергосистем можно отразить схематично на рис. 5.


Рис. 5. Методы расчета предельных режимов


Библиографический список

1. 
   Идельчик В.И. Расчеты и оптимизация режимов электрических сетей и систем. – М.: Энергоатомиздат, 1988.
   
2. 
   Идельчик В.И. Расчеты установившихся режимов электрических систем. – М.: Энегрия, 1977.
   
3. 
   Применение цифровых вычислительных машин в электроэнергетике /О.В. Щербачев, А.И. Зейлигер, К.П. Кадомская и др.; под ред. О.В. Щербачева/. – Л.: Энегрия, 1980.
   
4. 
   Жуков П.А., Стратин И.П. Установившиеся режимы сложных электрических сетей и систем: Методы расчетов. – М.: Энегрия, 1979.
   
5. 
   Гамм А.З. Методы расчета нормальных режимов электро-энергетических систем на ЭВМ. – Иркутск: Изд-во ИПИ, 1972.
   
6. 
   Баринов В.А., Совалов С .А. Режимы энергосистем: Методы анализа и управления. – М.: Энергоатомиздат, 1990.
   
7. 
   Фазилов Х.Ф. Методы режимных расчетов электрических систем. – Ташкент: Наука, 1964.
   
8. 
   Качанова Н.А. Электрический расчет сложных энергосистем на ЦВМ. – Киев: Наукова думка, 1966.
   
9. 
   Липес А.В., Окуловский С.К. Расчеты установившихся режимов электрических систем на ЭВМ. – Свердловск, УПИ, 1986.
   
10. 
    Конторович А.М., Шелухин Н.Н. Расчет режимов энергосистем при больших небалансах мощности и изменения частоты//Электричество. – 1982. - №7.
    
11. 
    Крюков А.В., Макаров Ю.В. Методы экспресс-расчетов установившихъся режимов электрических систем: Учебное пособие. – Улан-Удэ, Вост.-Сиб. технол. ин-т, 1990.
    
12. 
    Гончуков В.В., Горнштейн В.М., Крумм Л.А. и др Автоматизация управления энергообьединениями // М: Энергия.
    
13. 
    Идельчик В.И. Расчеты установившихся режимов// М: Энергия, 1977.
    
14. 
    Конторович А.М., Дунаева Н.П. Исследование методов расчета установившихся режимов, основанных на разложении решения в ряд Тейлора // Иркутск, 1978.
    
15. 
    Баринов В.А. Определение запаса статической апериодической устойчивости сложных электроэнергетических систем // Изв. АН СССР, Энергетика и транспорт, 1973, №1.
    
16. 
    Ножин Л.Э. Исследование статической устойчивости установившихся и самоустанавливающихся режимов электрических систем с помощью ЦВМ: Автореф. дис. ... канд.техн.наук.Л.,1970.
    
17. 
    Совалов С.А. Режимы единой энергосистемы. М.: Энергоиздат,1983.
    
18. 
    Цукерник Л.В. Основные положения анализа статической устойчивости сложных энергосистем при помощи вычислительных машин //Проблемы технической электродинамики. Киев: Наукова думка,1972.Вып.36.
    
19. 
    Цукерник Л.В. Учет влияния нелинейности математической модели энергосистемы при машинных методах расчета запаса ее устойчивости "в малом" // Проблемы нелинейной электротехники. Киев: Наукова думка,1984.
    
20. 
    Электрические системы / Под редакцией Веникова В.А. М.:Высшая школа,1982.
    
21. 
    Методы исследования устойчивости электрических систем и их использование // Сб. научных трудов ВНИИ Энергосетьпроект, М: Энергоатомиздат, 1985.
    
22. 
    Ушаков Е.И. Статическая устойчивость электрических систем // Сиб. энерг. ин-т, Новосибирск: Наука, 1988.
    
23. 
    Тьюарсон Р. Разряженные матрицы // М:Мир, 1977.
    
24. 
    Веников В.Н., Строев В.Н., Идельчик В.И., Тарасов В.И. Оценка статической устойчивости электрических систем на основе решения уравнений установившегося режима // Изв. АН СССР, Энергетика и транспорт, 1971, №5.
    
25. 
    Гончуков В.В., Горнштейн В.М., Крумм Л.А. и др Автоматизация управления энергообьединениями // М: Энергия, 1979.
    
26. 
    Веников В.А. Переходные электромеханические процессы в электрических системах. – М.: Высшая школа, 1985.
    
27. 
    Конторович А.М., Крюков А.В. Локализация слабых звеньев электрических систем с помощью практических критериев устойчивости. – Изв. вузов. Энергетика, 1983, №9.
    
28. 
    Тарасов В.И. Применение способа непрерывного утяжеления для определения предельных по апериодической устойчивости режимов электрических систем. – В кн.: Вопросы применения математических методов при управлении режимами и развитием электрических систем. Иркутск, 1975.
    
29. 
    Конторович А.М., Макаров Ю.В., Тараканов А.А. Совершенствование методов непрерывного утяжеления для определения предельных режимов электрических систем / Труды ЛПИ. – Л., 1982, №385.
    
30. 
    Конторович А.М., Крюков А.В. Определение предельных режимов способом непрерывного утяжеления // Л:ЛПИ, 1981,№ 380.
    
31. 
    Конторович А.М., Крюков А.В. Использование уравнений предельных режимов в задачах управления ЭЭС // Изв. АН СССР, Энергетика и транспорт, 1987, №3, с.25-33.
    
32. 
    Конторович А.М., Крюков А.В. Алгоритм решения вырожденных систем транцендентных уравнений//Тез. докл. XXVII научн. конф. ВСТИ. Улан-Удэ: Вост.-Сиб. технол.ин-т, 1988.
    
33. 
    Конторович А.М., Крюков А.В. Математическая модель предельных режимов энергосистем // Моделирование электроэнергетических систем. Тез.докл.Всес.научн.конф. Баку,1982.
    
34. 
    Конторович А.М., Крюков А.В. Предельные режимы энергосистем (Основы теории и методы расчетов). – Иркутск: Иркутский университет, 1985.
    
35. 
    Конторович А.М., Крюков А.В. Уравнения предельных режимов и их использование для решения задач управления энергосистемами. – В кн.: Методы исследования устойчивости сложных электрических систем и их использование. – М.: Энергия, 1985.
    
36. 
    Конторович А.М., Крюков А.В. Выделение слабых звеньев по статической устойчивости в сложных электрических системах. – Иркутск – Улан-Удэ, 1987. Деп. в Информэнерго, №2446-эн.
    
37. 
    Конторович А.М. Направление исследований по методам расчета режимов / Труды ЛПИ. – Л., 1985, №406.
    
38. 
    Конторович А.М., Лукина М.К. Построение областей устойчивости для трехмашинной эквивалентной схемы энергосистемы. – Л., 1984. Деп. в Информэнерго, №1517эн-Д84