|
|
леция по сейсмике. лекции по сейсморазведке2 (1). Введение сущность сейсморазведки Сейсмическая разведка (сейсморазведка)
2.2. Законы отражения
Рассмотрим законы отражения упругих волн, воспользовавшись принципом Ферма. Пусть в пласте Iв точке 0 расположен источник, от которого во все стороны распространяется волна со скоростью V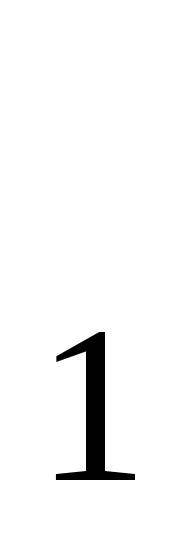 (рис. 2.2). (рис. 2.2).
О     С С
  I d I d 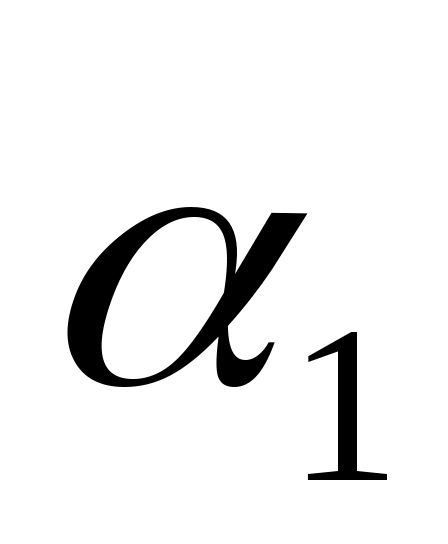 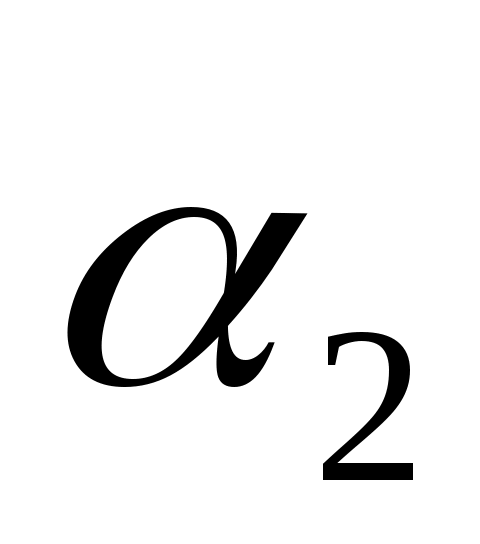 b b
  x x
В

a
Рис. 2.2. Отражение волны
На границе образуется отраженная волна распространяющаяся в слое I со скоростью V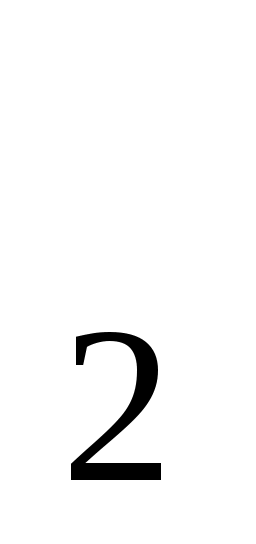 . В случае монотипной отраженной волны V . В случае монотипной отраженной волны V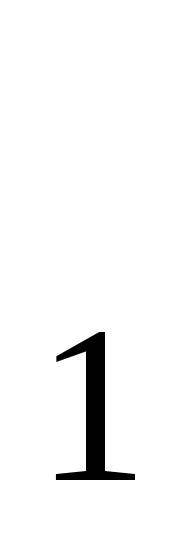 = V = V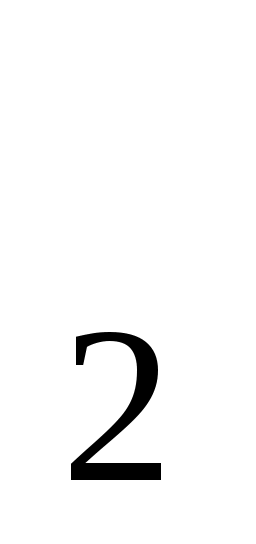 , в случае обменной отраженной волны V , в случае обменной отраженной волны V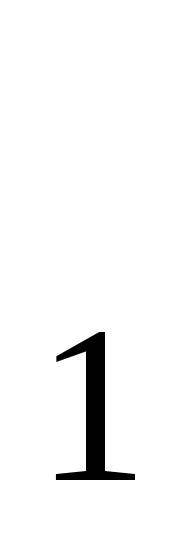 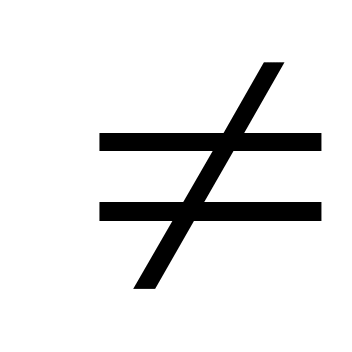 V V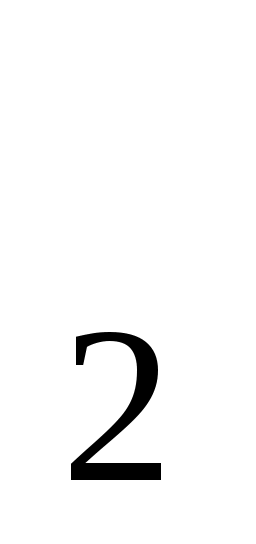 . Предположим, что луч падающей волны достигает границу раздела в точке В, аотраженнаяволна выходит в точку С. Положение точки В выбрано произвольно. Совместим с границей раздела ось координат x. Тогда рассматриваемые точки имеют координаты: О(0, d), В(x,0), С(a, b). Определим время пробега волны – t вдоль луча ОВС: . Предположим, что луч падающей волны достигает границу раздела в точке В, аотраженнаяволна выходит в точку С. Положение точки В выбрано произвольно. Совместим с границей раздела ось координат x. Тогда рассматриваемые точки имеют координаты: О(0, d), В(x,0), С(a, b). Определим время пробега волны – t вдоль луча ОВС:
t=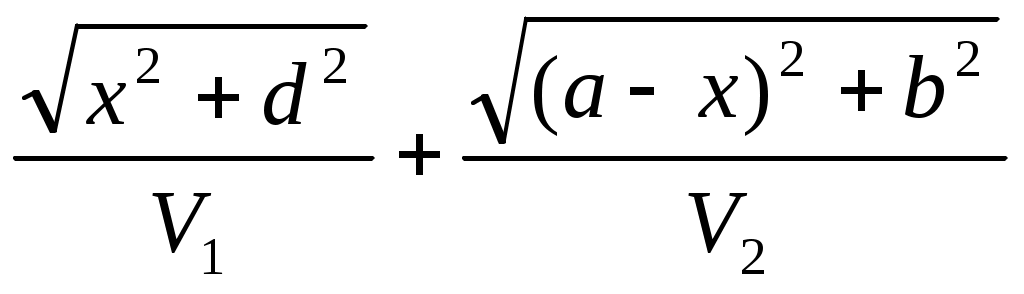 . (2.1) . (2.1)
По принципу Ферма точка В должна быть расположена так, чтобы время пробега волны по лучу было наименьшим. Определим значение координаты x при которой выполняется это требование, приравняв к нулю производную 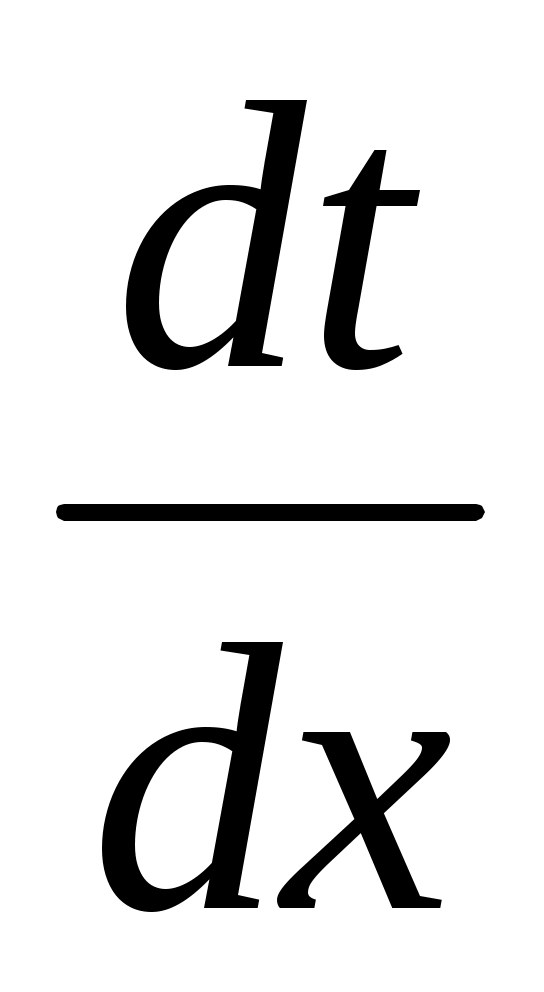 : :
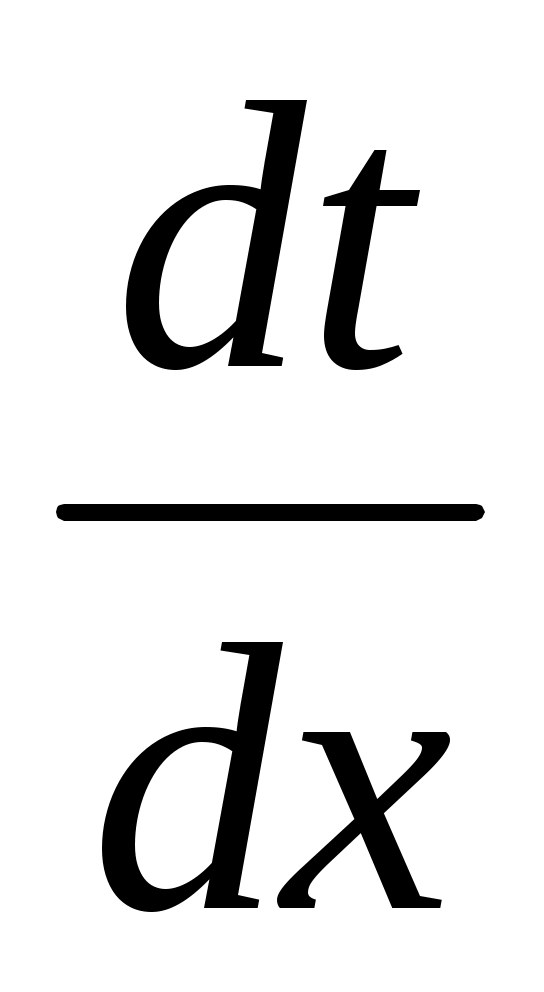 = =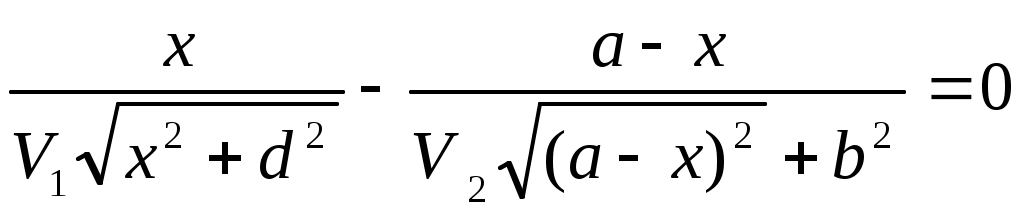 . (2.2) . (2.2)
Согласно рис. 2.2,

Sin 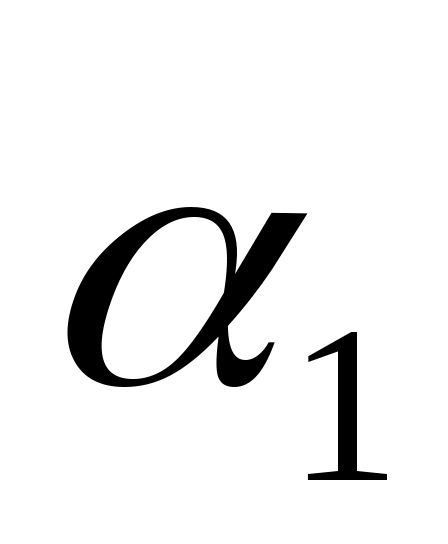 = =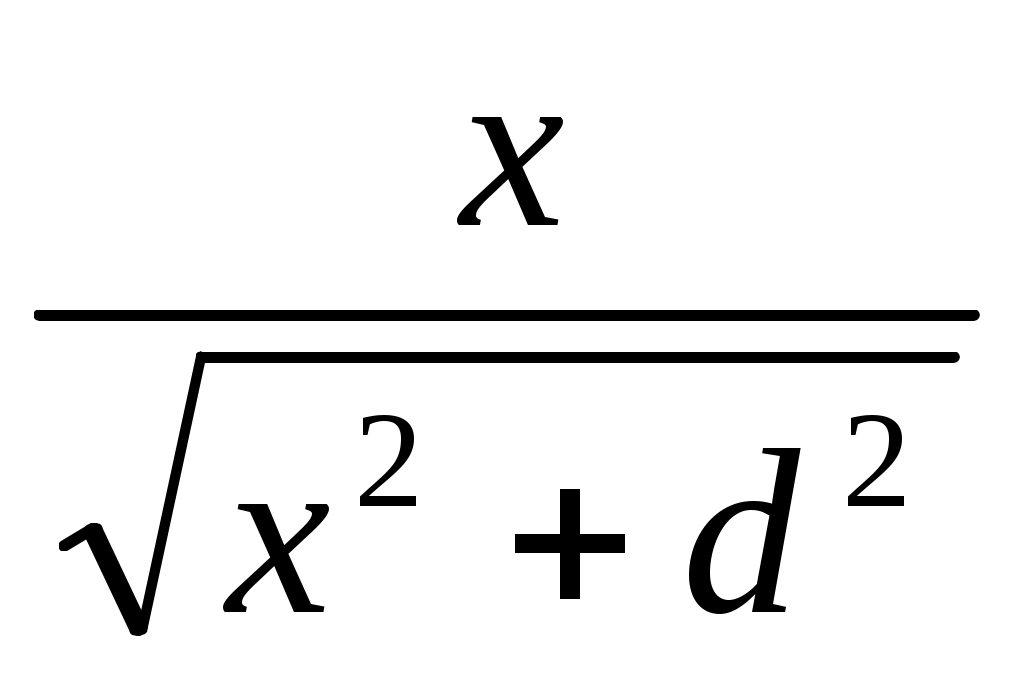 ; Sin ; Sin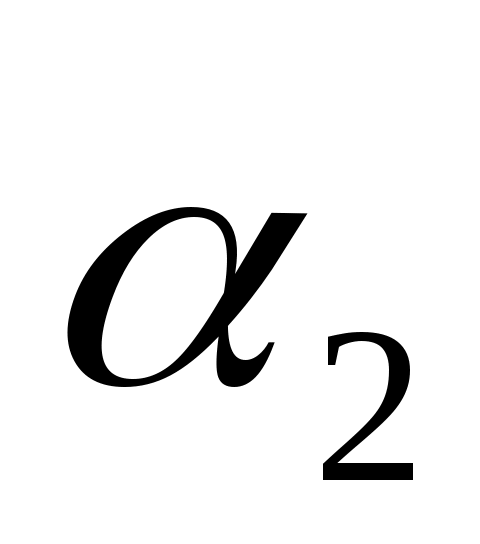 = =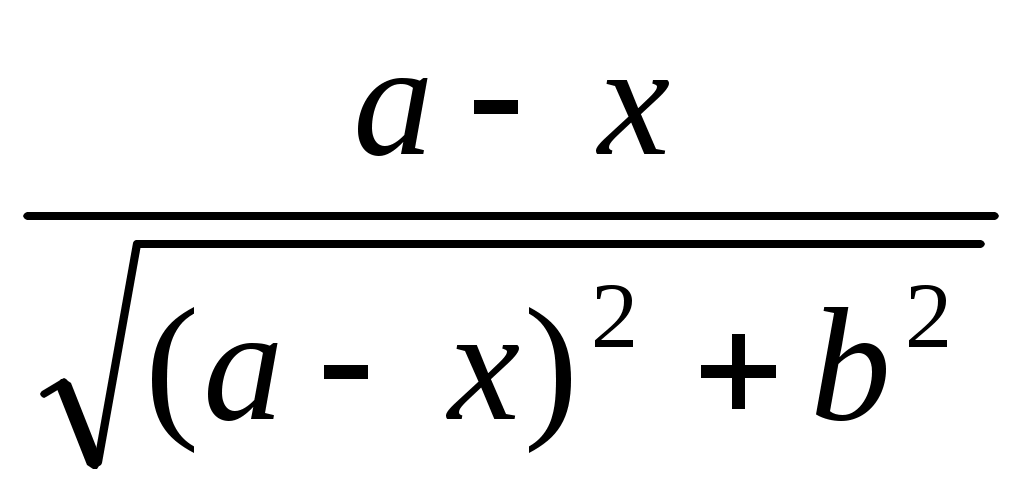 , (2.3) , (2.3)
где 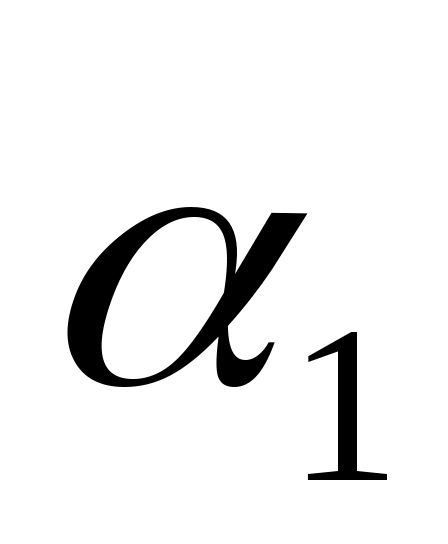 - угол падения, - угол падения, 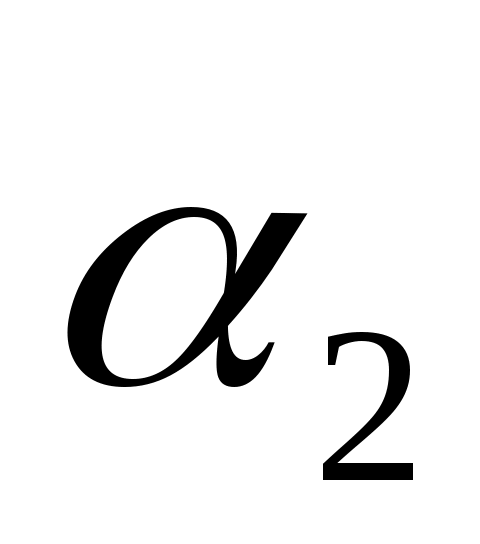 - угол отражения. Тогда из уравнения (2.2) получим: - угол отражения. Тогда из уравнения (2.2) получим:
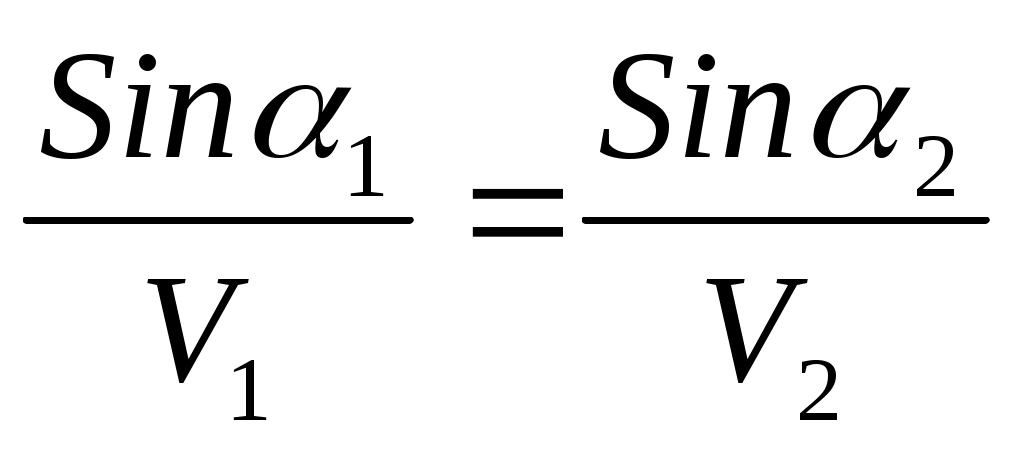 . (2.4) . (2.4)
Это соотношение выражает закон отражения (закон Снеллиуса) в общей форме, который справедлив для обменных волн. В случае отражения монотипной волны, когда V = V = V получим получим
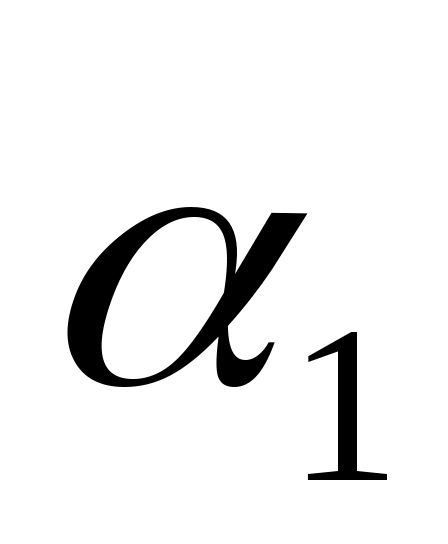 = =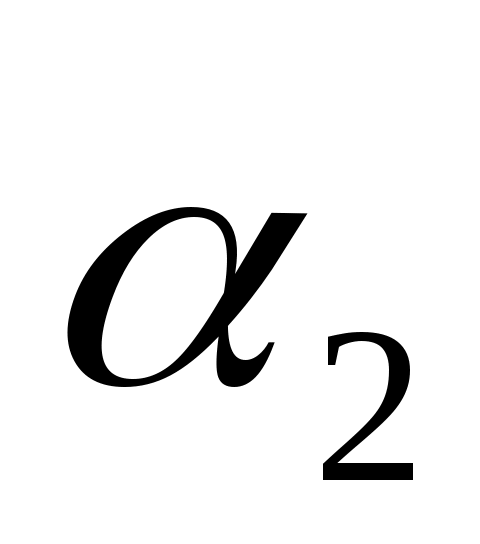 , (2.5) , (2.5)
т.е. угол отражения равен углу падения.
Рассмотрим зависимость между амплитудами отраженной и падающей волн вблизи границы раздела двух сред. Пусть а - амплитуда падающей продольной волны Р - амплитуда падающей продольной волны Р , а , а - амплитуда отраженной продольной волны Р - амплитуда отраженной продольной волны Р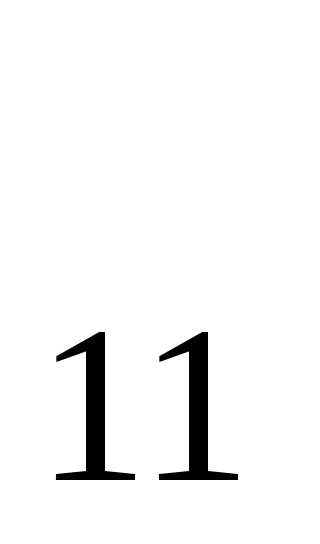 , а , а - амплитуда отраженной поперечной волны Р - амплитуда отраженной поперечной волны Р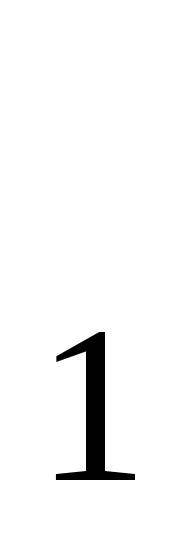 S S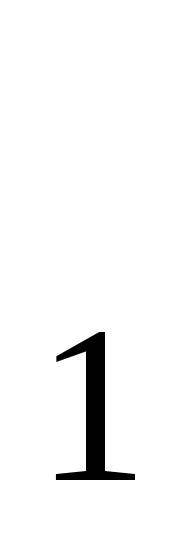 . Соотношения: . Соотношения:
A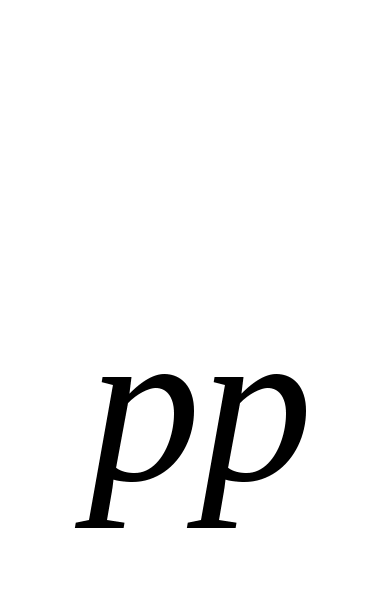 = =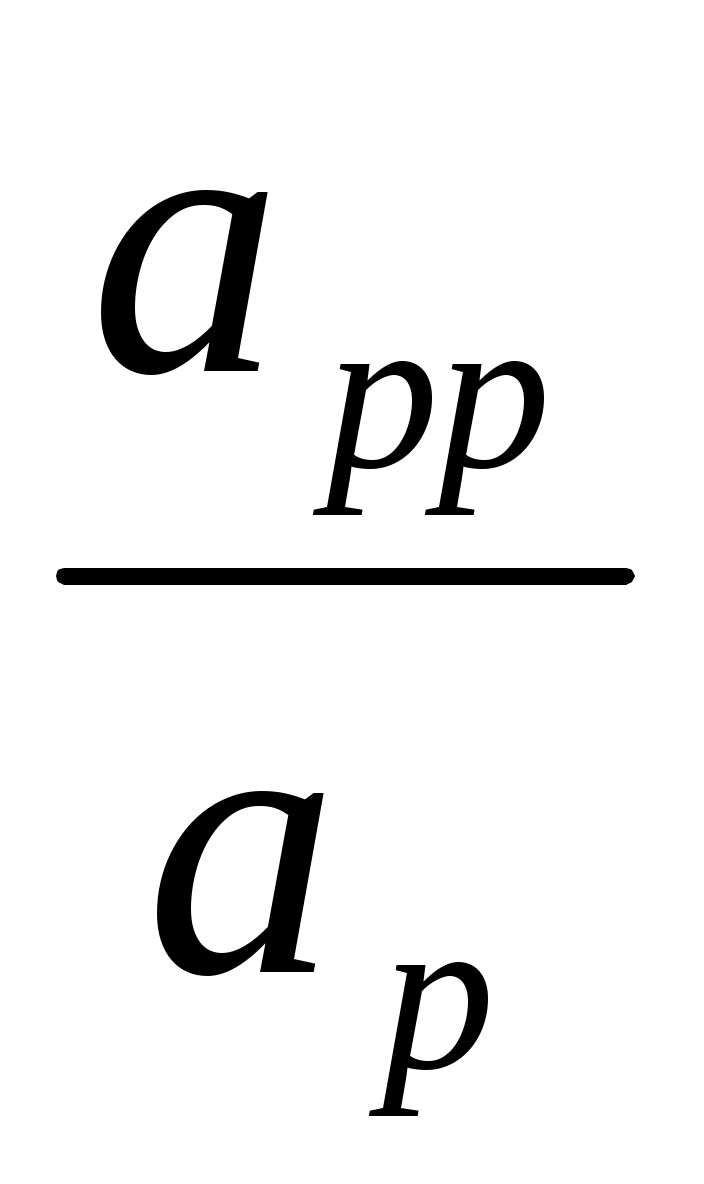 , A , A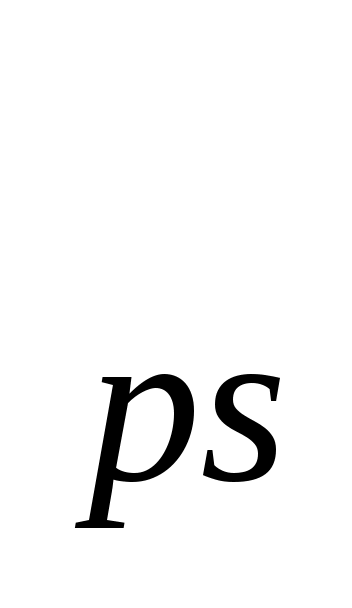 = =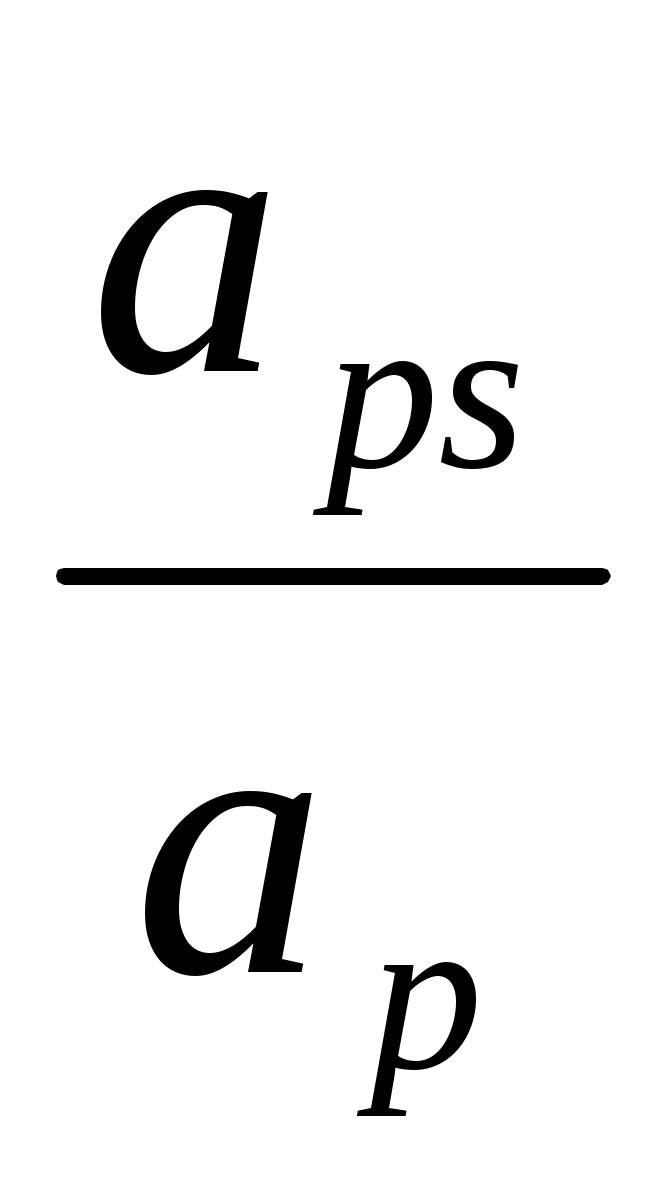 , (2.6) , (2.6)
Называются коэффициентами отражения. Они определяют амплитуды отраженных волн сравнительно с амплитудой падающей волны. Коэффициенты отражения сложным образом зависят от угла падения  , скоростей и плотностей в средах, прилегающих к границе раздела. В случае нормального падения, когда луч перпендикулярен границе и, следовательно, , скоростей и плотностей в средах, прилегающих к границе раздела. В случае нормального падения, когда луч перпендикулярен границе и, следовательно,  =0 коэффициенты отражения соответствуют следующим выражениям: =0 коэффициенты отражения соответствуют следующим выражениям:
A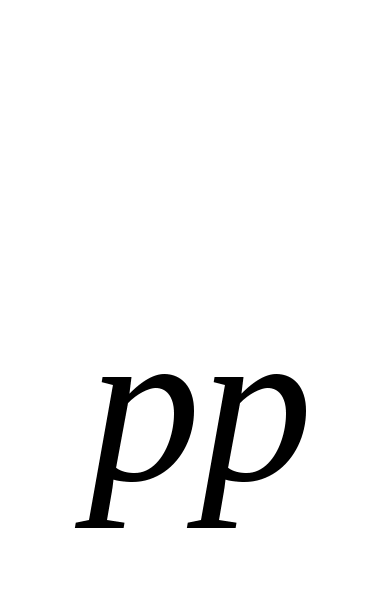 = =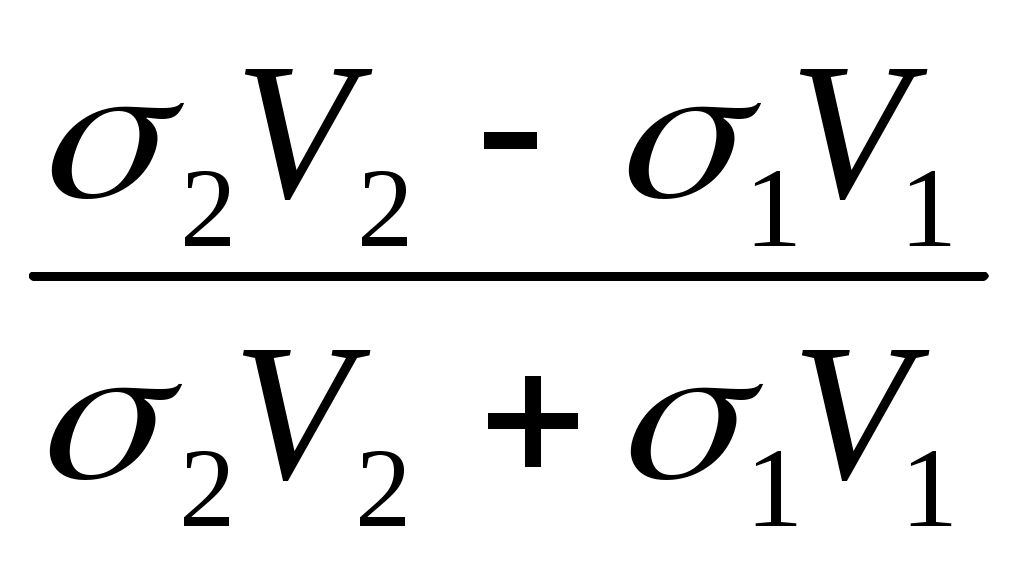 , A , A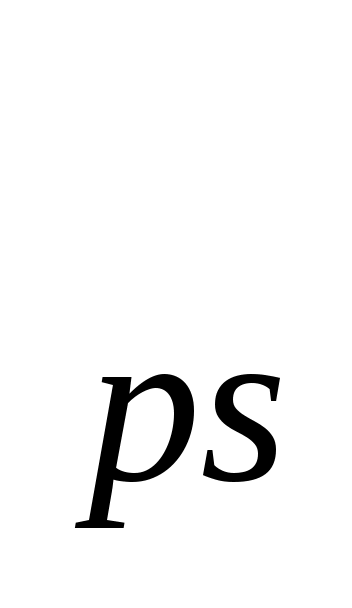 =0. (2.7) =0. (2.7)
Произведение 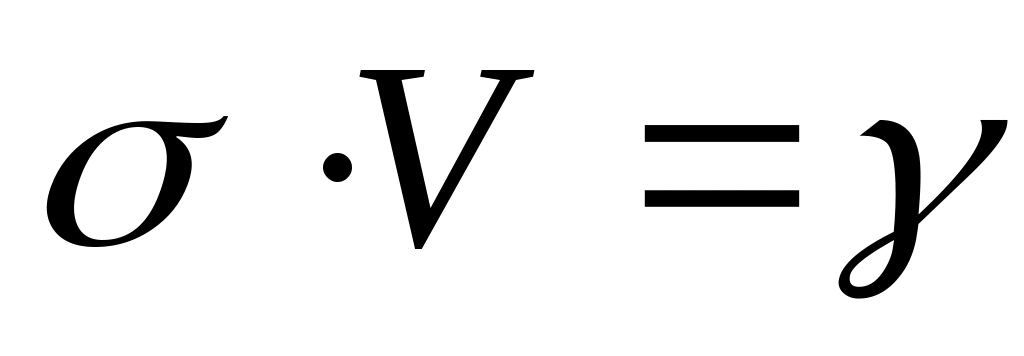 называют волновым сопротивлением или акустической жесткостью среды. Из уравнения (2.7) видно, что отраженная волна образуется при условии: называют волновым сопротивлением или акустической жесткостью среды. Из уравнения (2.7) видно, что отраженная волна образуется при условии:
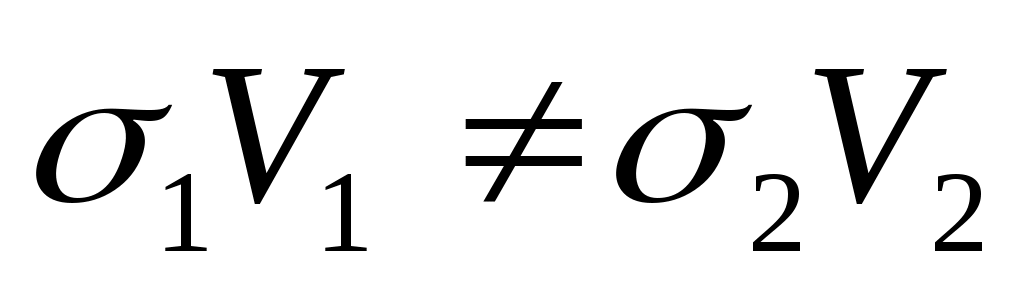 . (2.8) . (2.8)
Следовательно, отраженные волны образуются на границах пластов с различными волновыми сопротивлениями. Такие границы называют отражающими. Чем больше различие волновых сопротивлений по обе стороны отражающей границы, тем больше амплитуда отраженной от неё волны. Из формулы (2.7) видно, что при нормальном падении луча ( =0), возникают только монотипные отраженные волны. Обменная отраженная волна образуется, когда угол падения отличен от нуля. Существуют специальные таблицы и графики, при помощи которых можно определить коэффициенты отражения волн при различных углах падения. =0), возникают только монотипные отраженные волны. Обменная отраженная волна образуется, когда угол падения отличен от нуля. Существуют специальные таблицы и графики, при помощи которых можно определить коэффициенты отражения волн при различных углах падения.
2.3. Закон преломления
Определим положение фронта проходящей волны, воспользовавшись принципом Гюйгенса. Рассмотрим два пласта разделенные плоской границей R (рис. 2.3). Скорость волны в среде I равна V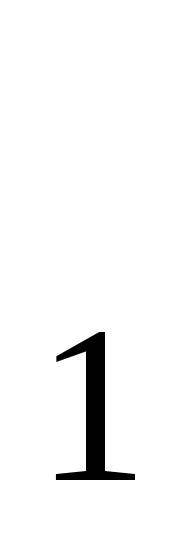 , в среде II - V , в среде II - V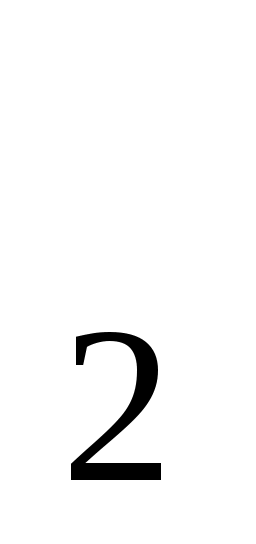 . Плоскийфронт падающей волны составляет угол . Плоскийфронт падающей волны составляет угол  с границей R. с границей R.

Рис. 2.3. Преломление волны
В момент времени t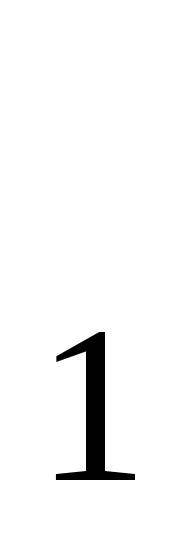 фронт падающей волны - L фронт падающей волны - L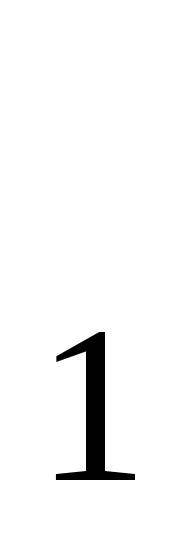 достиг границы в точке С достиг границы в точке С . Найдем положение фронта в последующий момент времени t . Найдем положение фронта в последующий момент времени t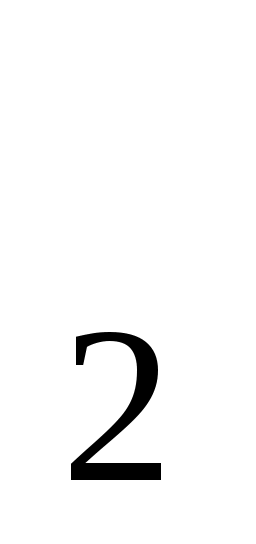 = t = t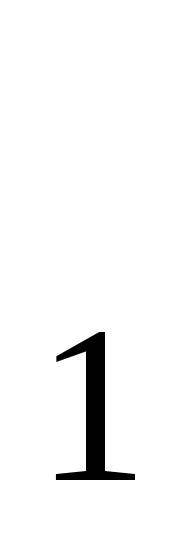 +∆t. Согласно принципу Гюйгенса, следует рассмотреть произвольные точки С +∆t. Согласно принципу Гюйгенса, следует рассмотреть произвольные точки С , С , С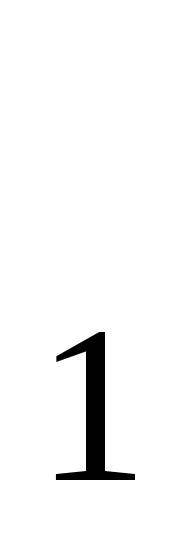 , С , С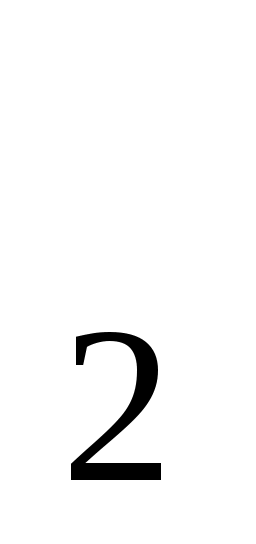  принадлежащие изохроне L принадлежащие изохроне L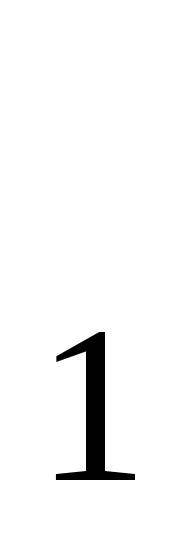 и являющиеся элементарными источниками колебаний. Определим радиусы элементарных фронтов волн, т.к. V и являющиеся элементарными источниками колебаний. Определим радиусы элементарных фронтов волн, т.к. V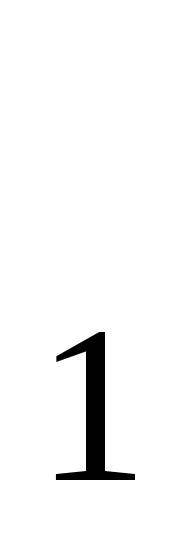 =constрадиусы одинаковы и равны =constрадиусы одинаковы и равны  = =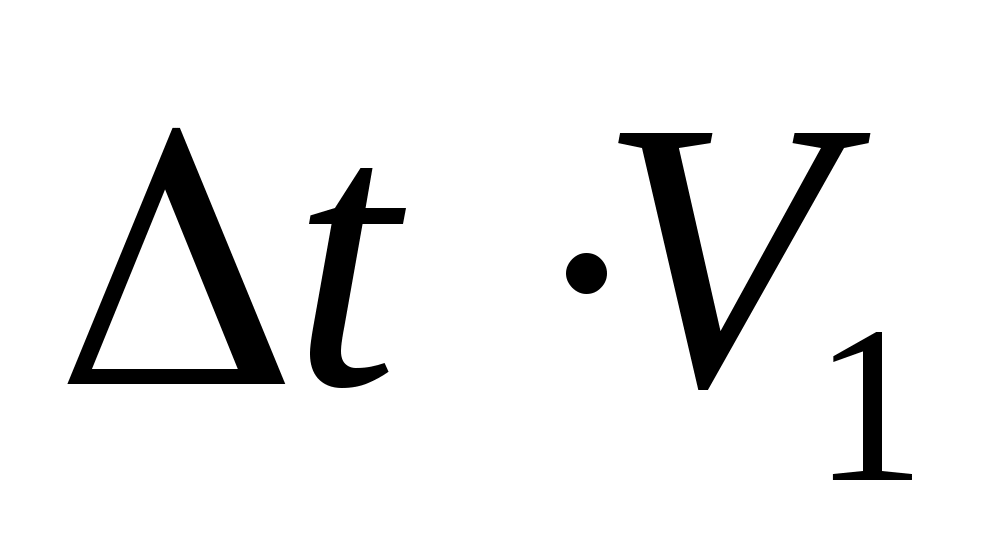 . .
Так как точка С находится на границе и одновременно принадлежит, как верхней так и нижней среде, она будет являться источником злементарных колебаний в среде II. Радиус полусферы равен находится на границе и одновременно принадлежит, как верхней так и нижней среде, она будет являться источником злементарных колебаний в среде II. Радиус полусферы равен 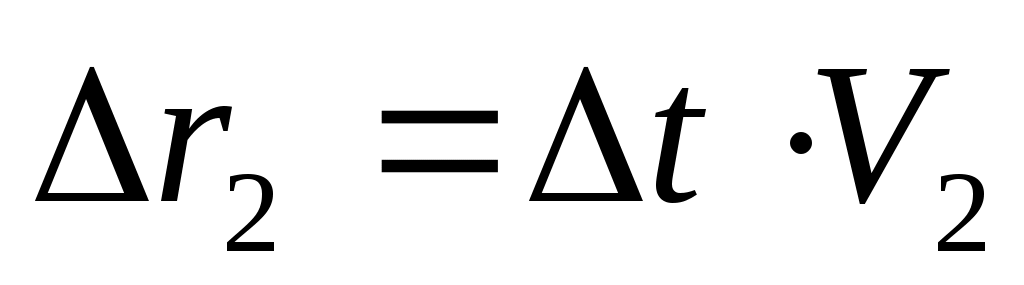 . Проведя огибающую ко всем полусферам, построим положение фронта L . Проведя огибающую ко всем полусферам, построим положение фронта L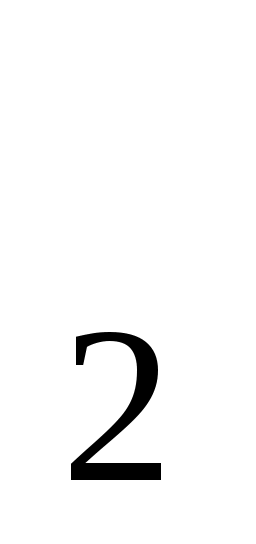 на момент времени t на момент времени t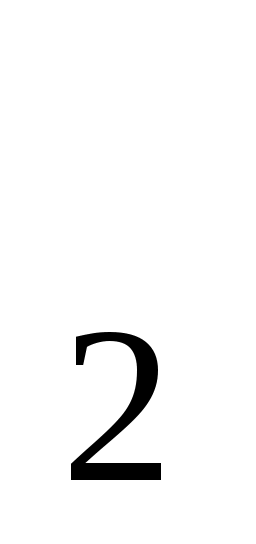 . Как видно из рисунка на границе фронт преломлен. Обозначим угол преломления β, который составляет фронт проходящей волны с границей раздела. Рассматривая прямоугольные треугольники с общей гипотенузой, получим: . Как видно из рисунка на границе фронт преломлен. Обозначим угол преломления β, который составляет фронт проходящей волны с границей раздела. Рассматривая прямоугольные треугольники с общей гипотенузой, получим:
С E E = =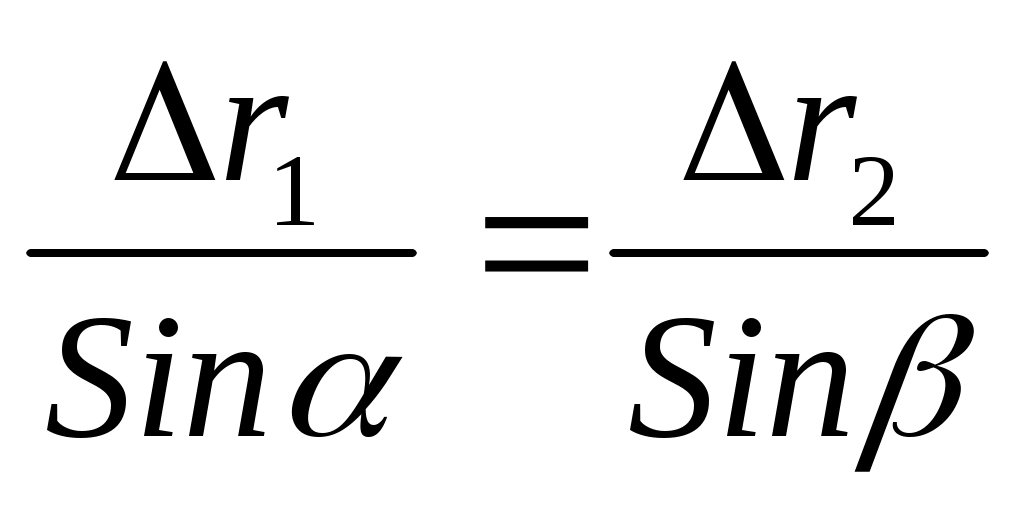 . (2.9) . (2.9)
Подставив значения  = =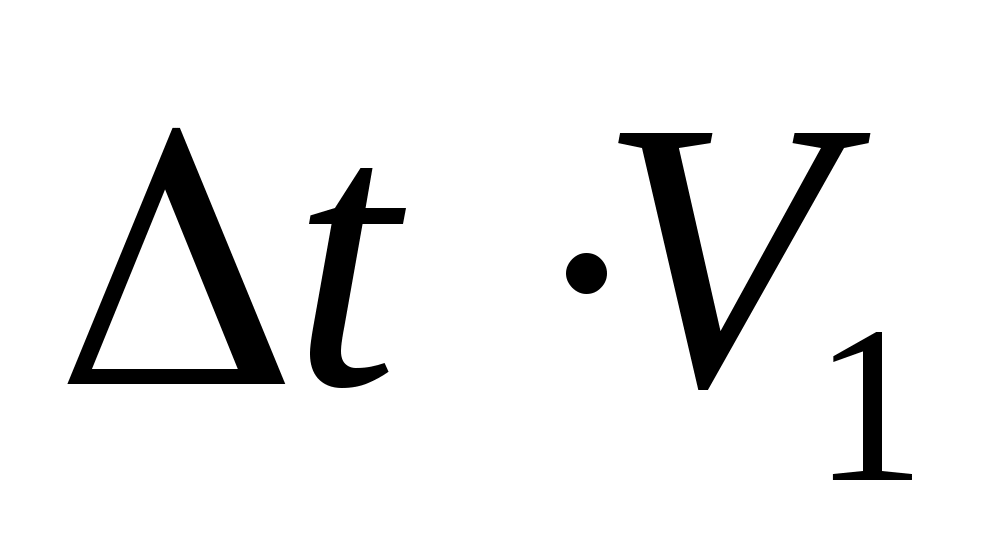 и и 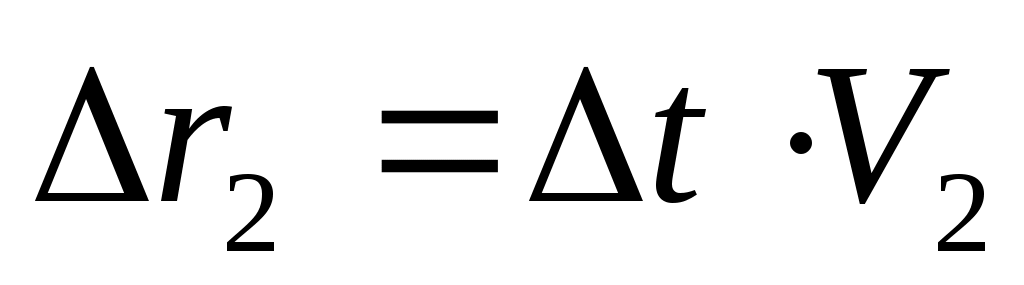 , получим закон преломления (закон Снеллиуса): , получим закон преломления (закон Снеллиуса):
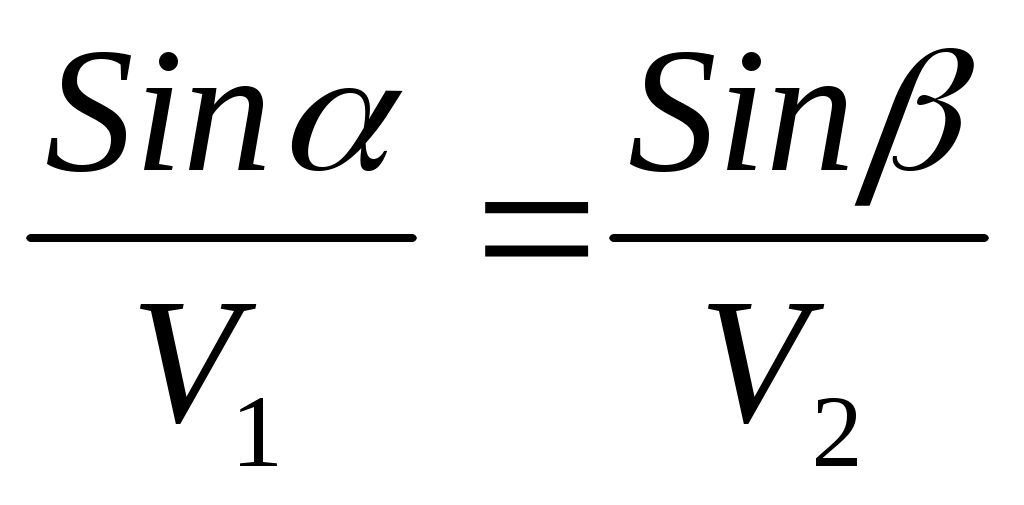 или или 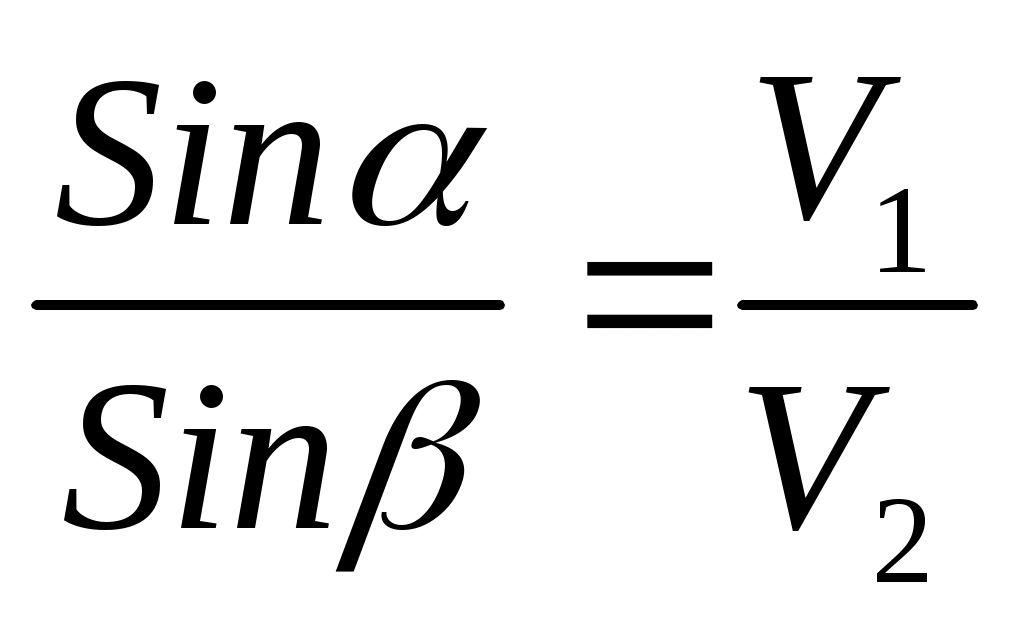 . (2.10) . (2.10)
Закон преломления в данном виде справедлив как для монотипных, так и для обменных волн.
Связь между амплитудами b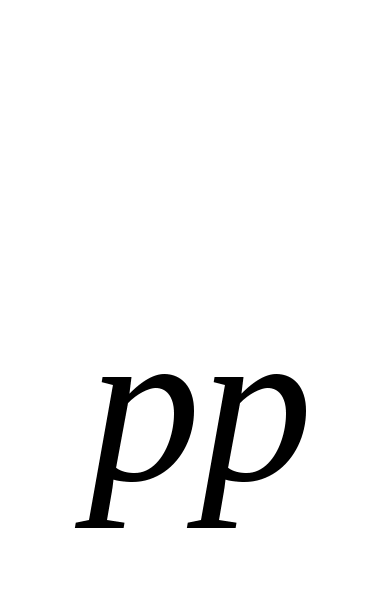 - продольной проходящей волны P - продольной проходящей волны P , b , b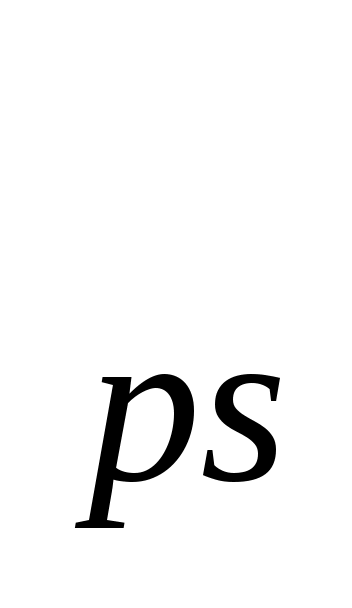 - поперечной проходящей волны - поперечной проходящей волны 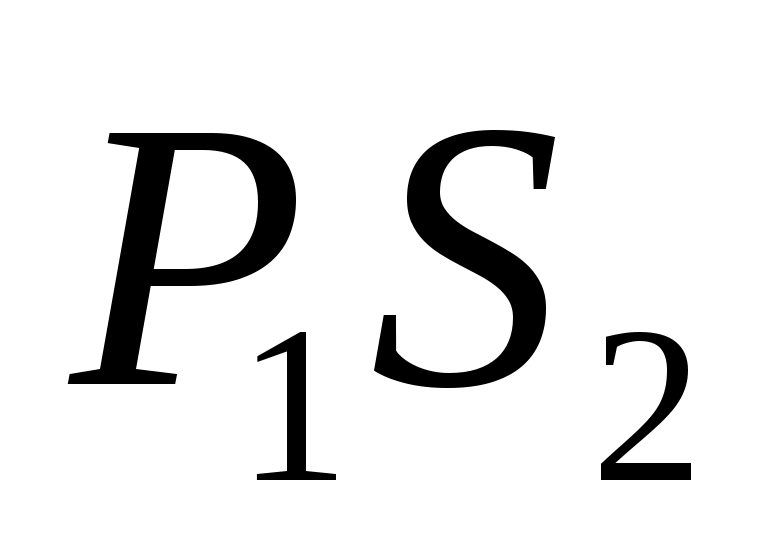 и продольной падающей волны - а и продольной падающей волны - а определяет коэффициенты прохождения (прозрачности): определяет коэффициенты прохождения (прозрачности):
B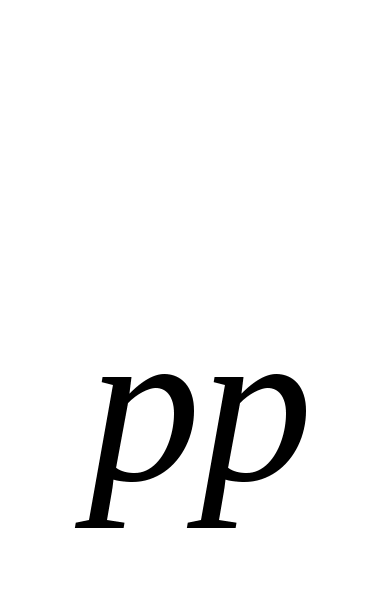 = =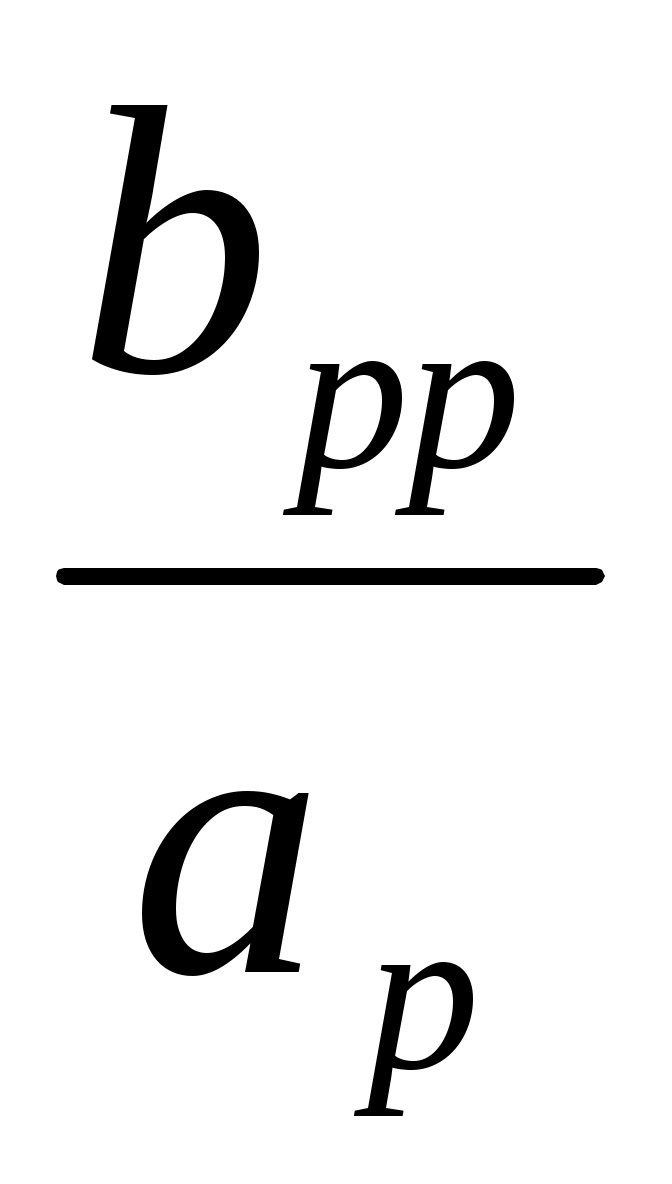 , B , B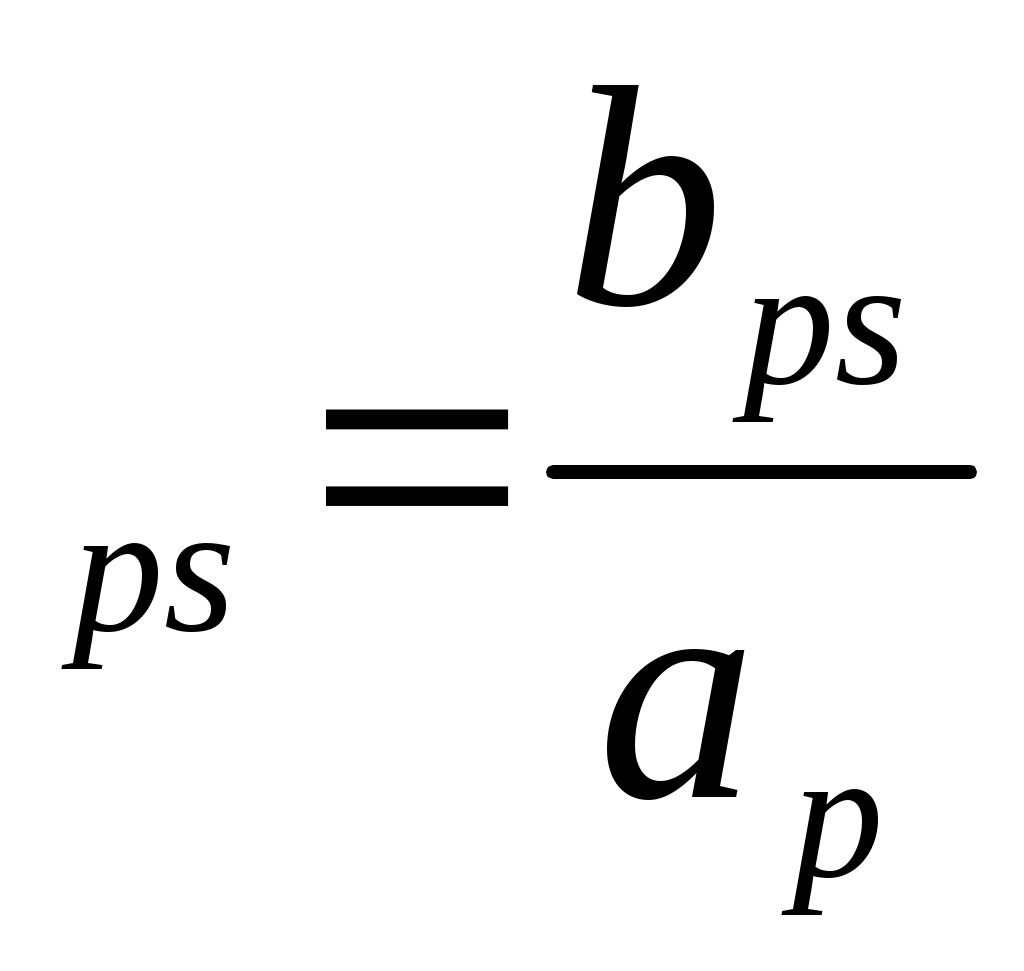 . (2.11) . (2.11)
В частном случае, при падение луча по нормали к границе ( =0) справедливы соотношения: =0) справедливы соотношения:
B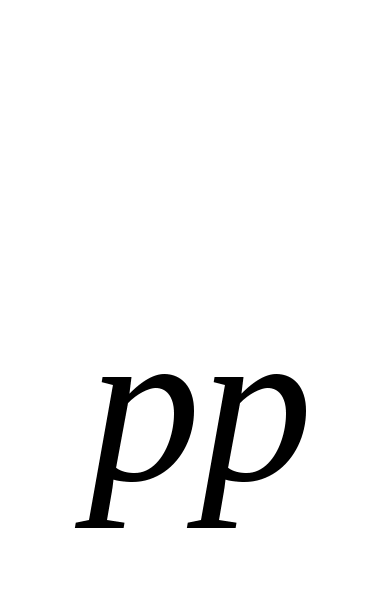 = =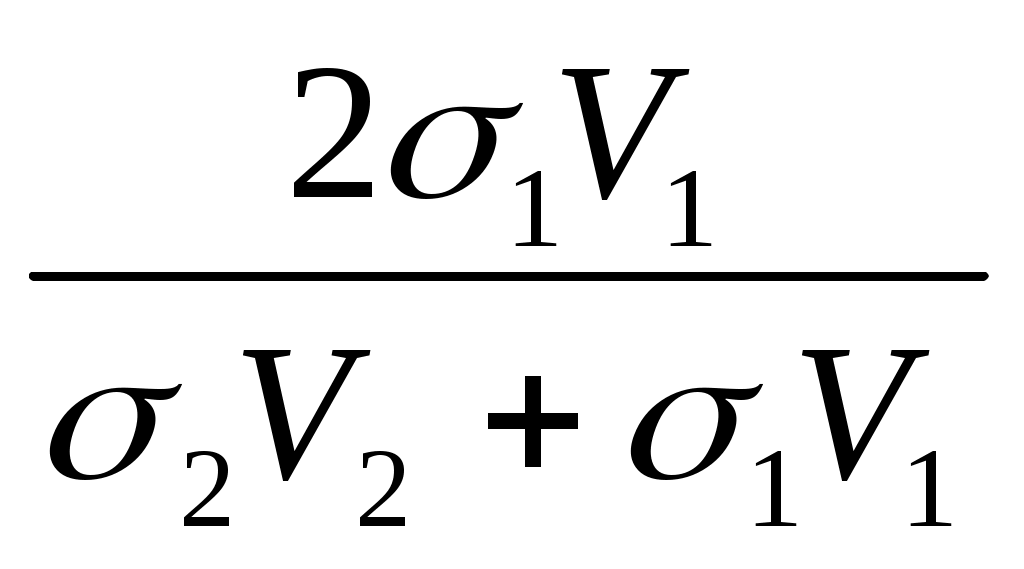 , B , B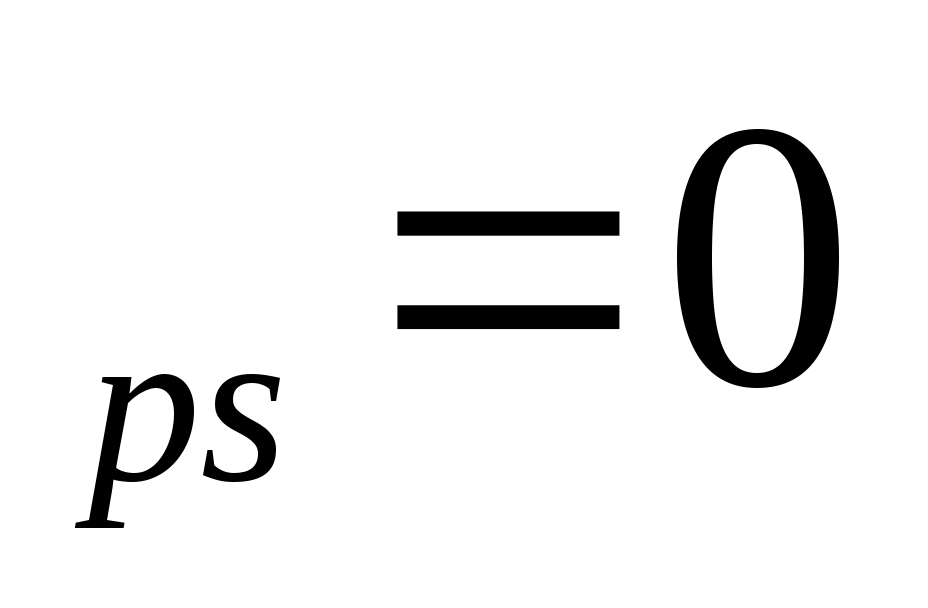 . (2.12) . (2.12)
Как и в случае отражения, при нормальном падении, не возникает обменных проходящих волн. Они образуются только при углах  , отличающихся от нуля. , отличающихся от нуля.
2.4. Образование головных (преломленных) волн
Для сейсморазведки особый интерес представляет явление полного внутреннего отражения. Это явление может иметь место только при условии, когда скорость V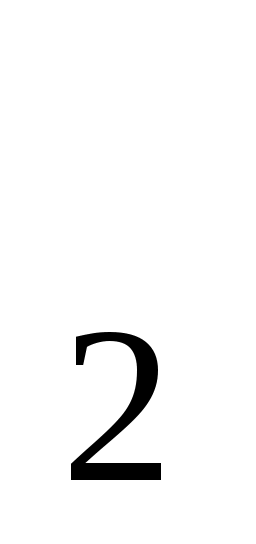 во второй среде больше скорости V во второй среде больше скорости V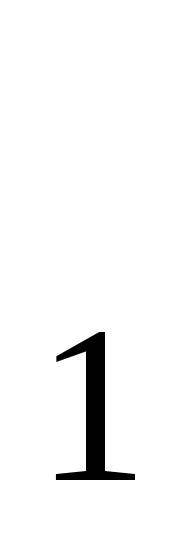 в первой среде. Тогда угол падения в первой среде. Тогда угол падения  =i, который называется критическим углом или углом полного внутреннего отражения.При выполнении первых двух условий угол преломления β становится равным =i, который называется критическим углом или углом полного внутреннего отражения.При выполнении первых двух условий угол преломления β становится равным  . Согласно закону преломления формула . Согласно закону преломления формула
(2.10) будет иметь следующий вид
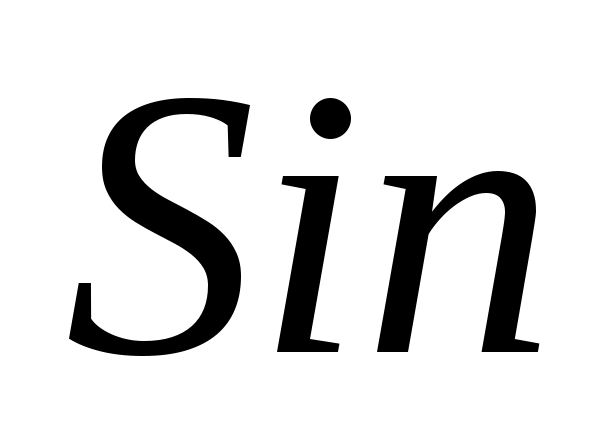 i= i=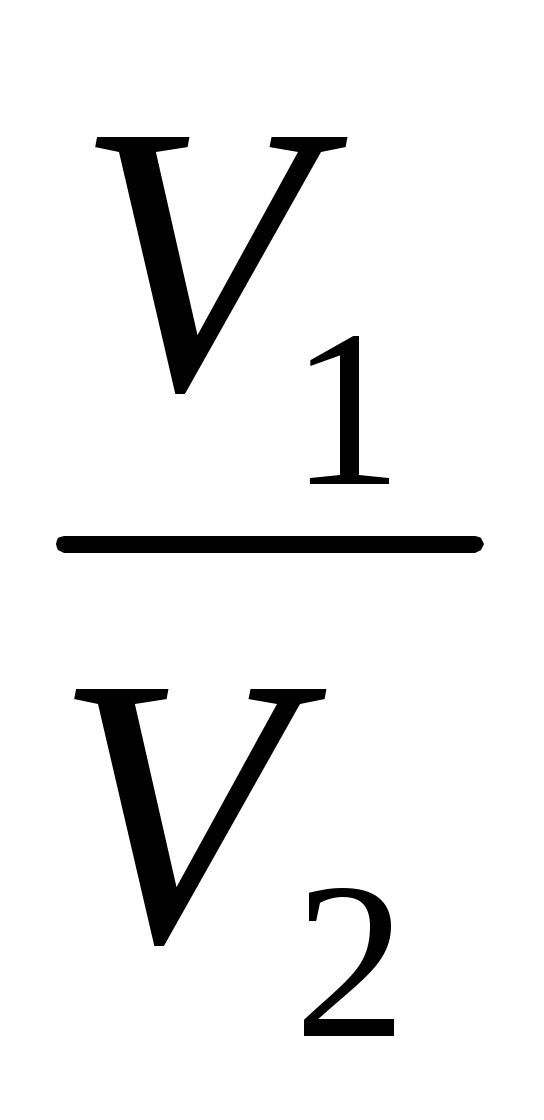 . (2.13) . (2.13)
В результате во второй среде вдоль границы раздела распространяется скользящая волна - P со скоростью V со скоростью V (рис. 2.4). Начальная точка формирования скользящей волны – Nназывается критической, аскорость распространения этой волны получила название граничной. В силу принципа Гюйгенса фронт скользящей волны будет формировать в верхней среде вторичные, так называемые головные или преломленные - P (рис. 2.4). Начальная точка формирования скользящей волны – Nназывается критической, аскорость распространения этой волны получила название граничной. В силу принципа Гюйгенса фронт скользящей волны будет формировать в верхней среде вторичные, так называемые головные или преломленные - P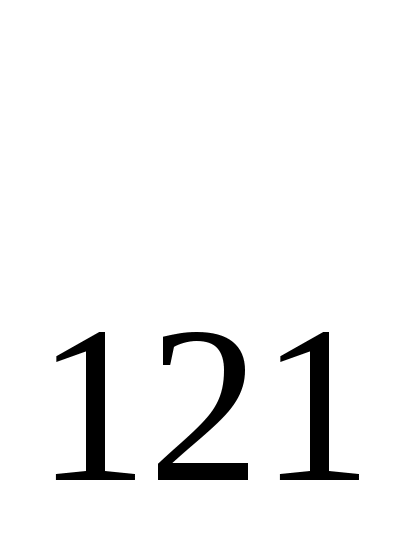  волны. Фронт этой волны будет плоским и наклонным к границе раздела под постоянным углом, а лучи взаимно параллельны и составляют с нормалью к границе угол i. Границу, на которой образуются головные волны, называют преломляющей. волны. Фронт этой волны будет плоским и наклонным к границе раздела под постоянным углом, а лучи взаимно параллельны и составляют с нормалью к границе угол i. Границу, на которой образуются головные волны, называют преломляющей.
   P P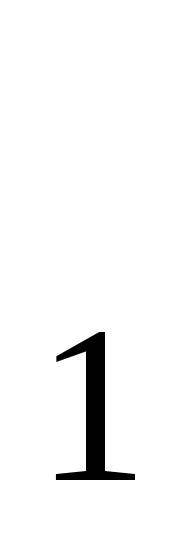 начальный лучP начальный лучP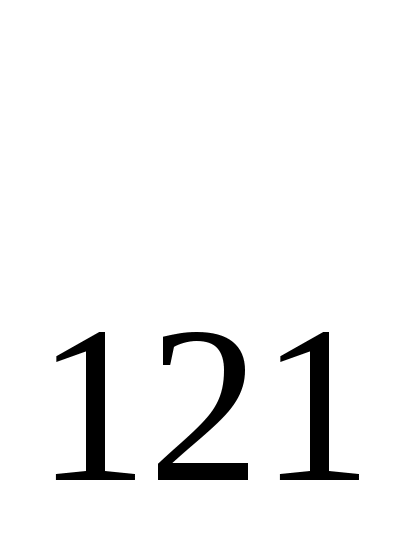
  
  iiфронт головной iiфронт головной
  V V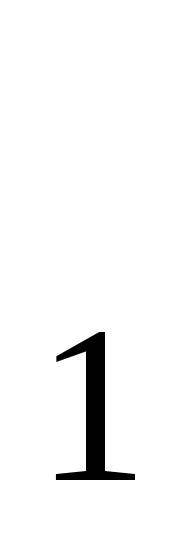 i волныV i волныV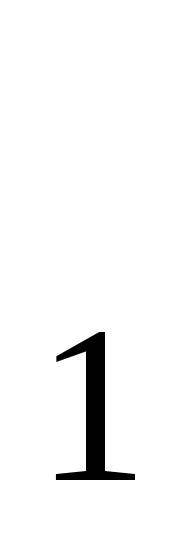 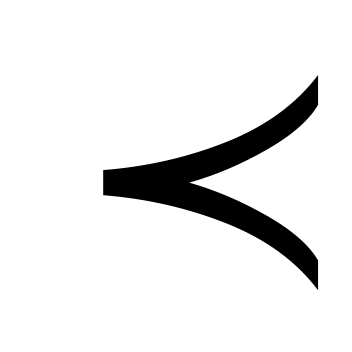 V V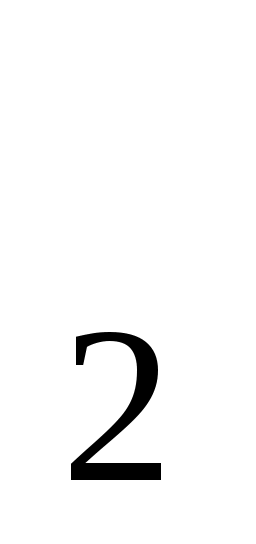
 
 N N 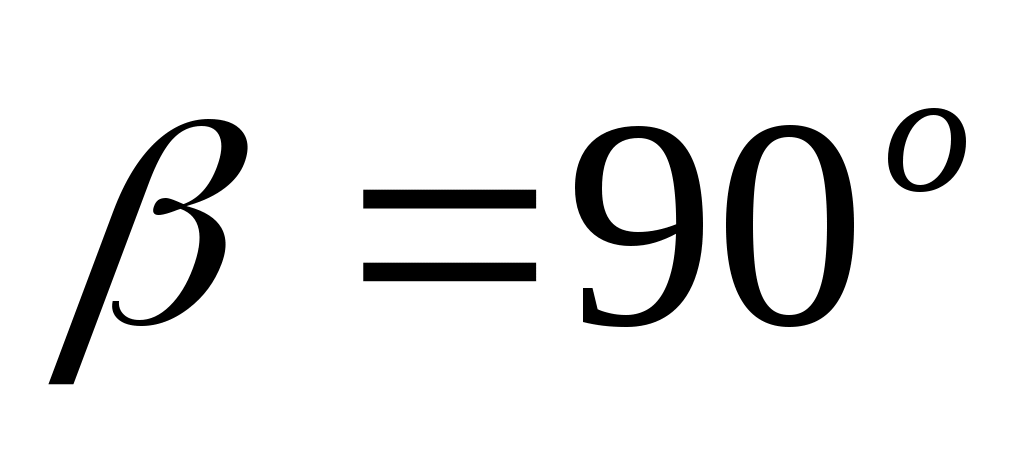 P P
V
Рис. 2.4. Образование головной (преломленной) волны
Помимо монотипной продольной преломленной волны P , рассмотренной на рис. 2.4., возможно образование обменных волн различных типов: P , рассмотренной на рис. 2.4., возможно образование обменных волн различных типов: P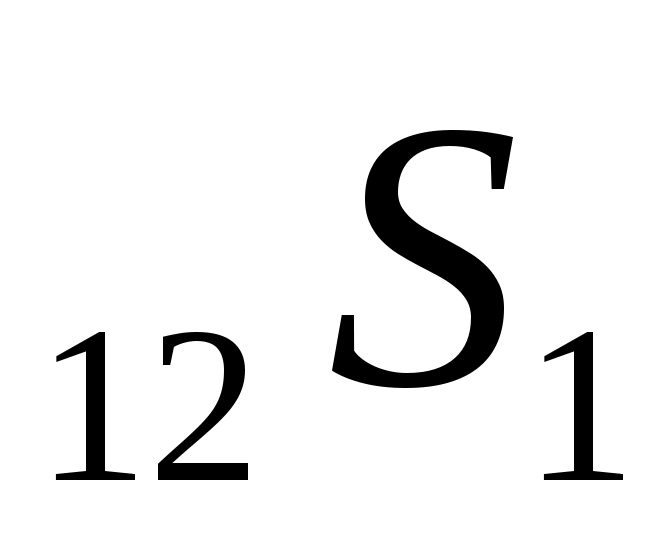 , P , P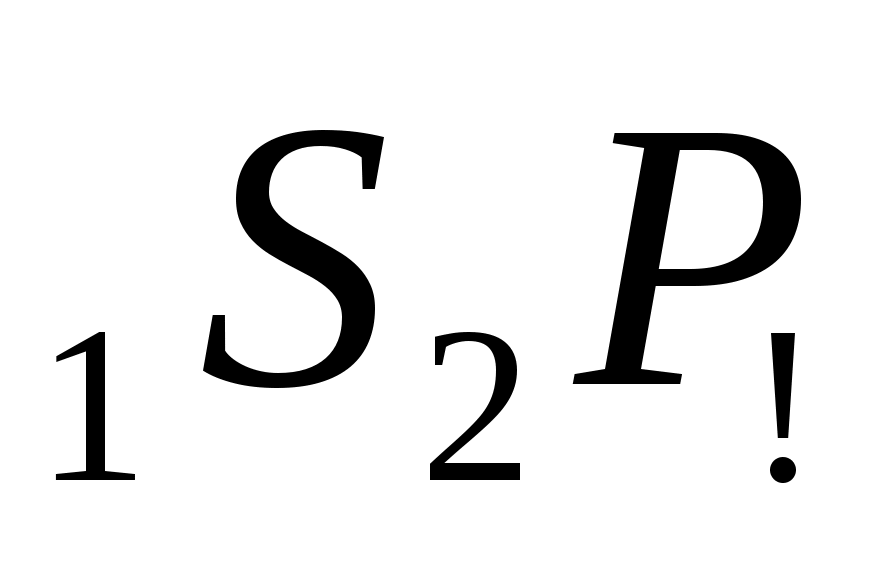 , P , P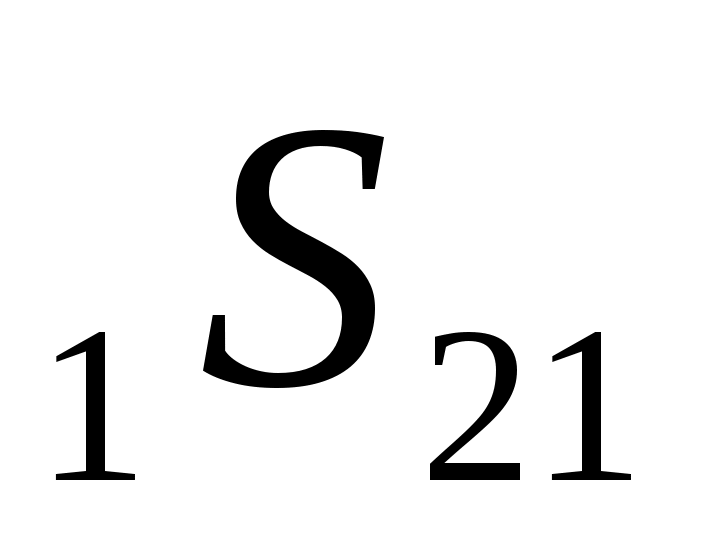 . .
Особенности головных (преломленных) волн 1. Преломленные волны всех типов можно наблюдать на поверхности земли только на некотором удалении от источника. Точка на линии профиля (х ), где впервые регистрируется преломленная волна, называется начальной точкой. ), где впервые регистрируется преломленная волна, называется начальной точкой.
2. Быстрое убывание амплитуды (от точки Nдо  ), связано с тем, что при движении скользящей волны P ), связано с тем, что при движении скользящей волны P вдоль преломляющей границы часть переносимой ею энергии расходуется на образование головной волны и не компенсируется энергией из преломляющего пласта. Отсюда следует, что амплитуда головной волны убывает с расстоянием быстрее, чем амплитуда отраженной волны от той же границы раздела вдоль преломляющей границы часть переносимой ею энергии расходуется на образование головной волны и не компенсируется энергией из преломляющего пласта. Отсюда следует, что амплитуда головной волны убывает с расстоянием быстрее, чем амплитуда отраженной волны от той же границы раздела
а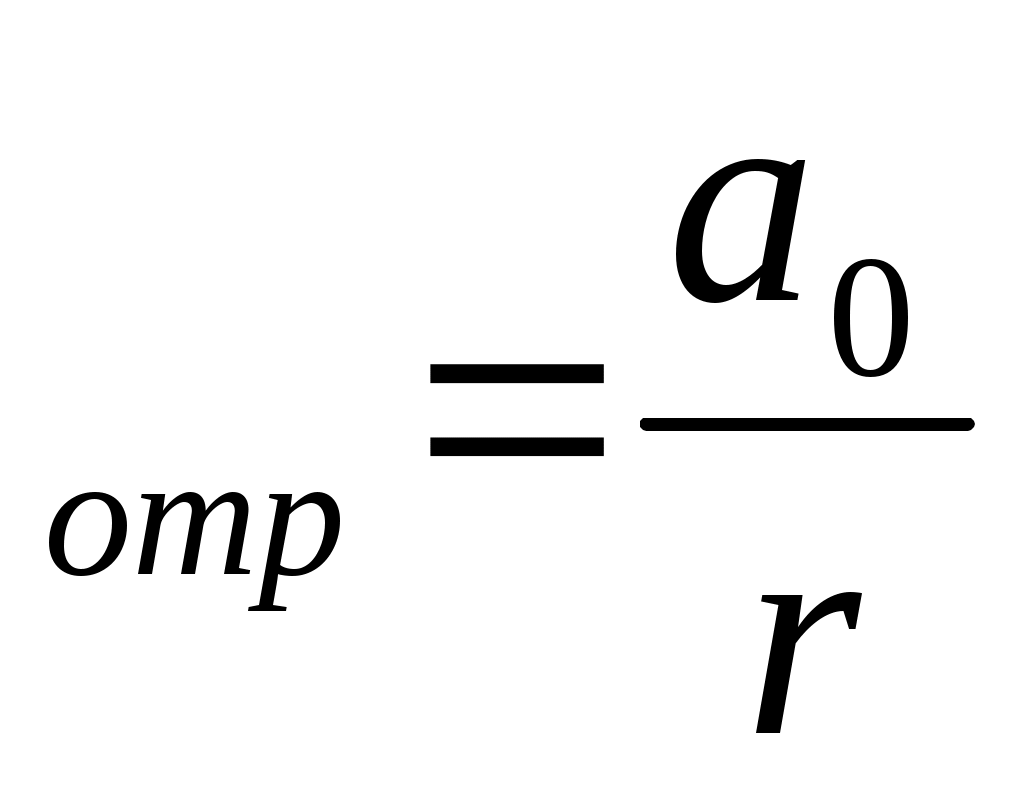  ; а ; а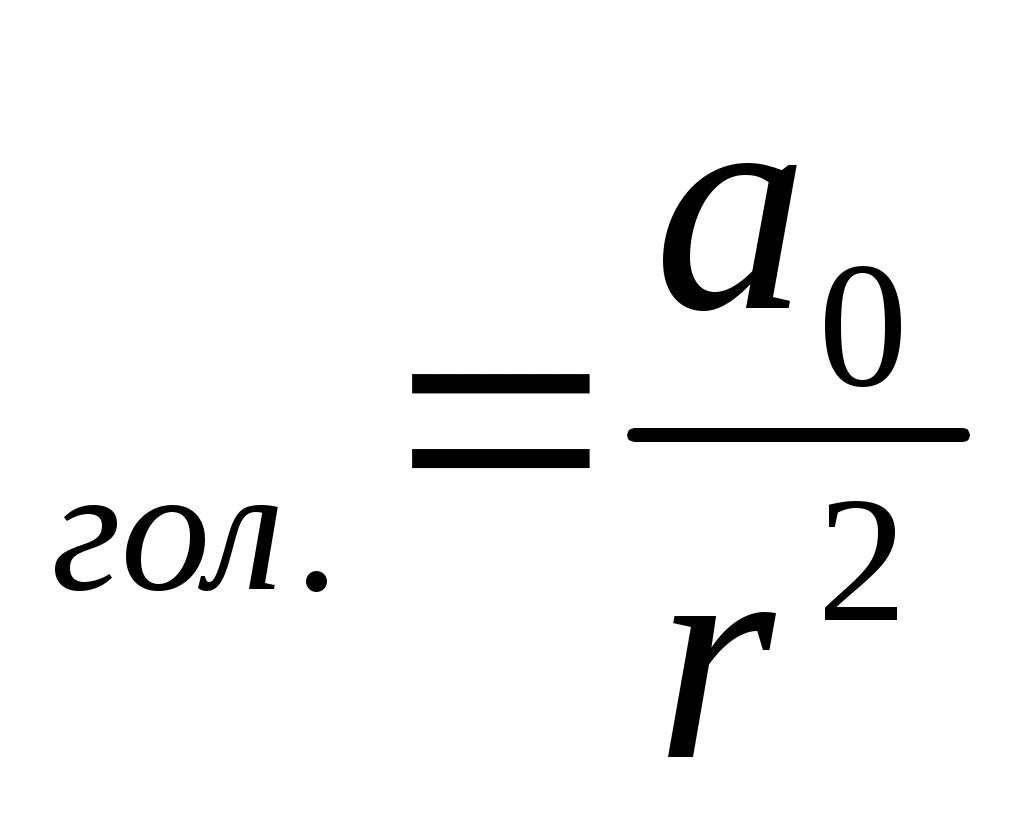 (2.14) (2.14)
3. Головная волна характеризуется более низкой видимой частотой по сравнению с падающей, отраженной или проходящей. |
|
|
 Скачать 3.3 Mb.
Скачать 3.3 Mb.


 С
С 
 I d
I d 
 x
x 



 P
P



 iiфронт головной
iiфронт головной
 V
V

 N
N 