леция по сейсмике. лекции по сейсморазведке2 (1). Введение сущность сейсморазведки Сейсмическая разведка (сейсморазведка)

• Название: Введение сущность сейсморазведки Сейсмическая разведка (сейсморазведка)
• Анкор: леция по сейсмике
• Дата: 13.02.2023
• Размер: 3.3 Mb.
• Имя файла: лекции по сейсморазведке2 (1).doc
• Тип: Документы; #933954
• страница: 2 из 5

1.4. Принципы геометрической сейсмики

Процесс распространения сейсмических волн в упругих средах подчиняется ряду важных для теории и практики принципам (постулатам).

Согласно принципу Ферма, время движения волны по лучу минимально. На основе этого принципа сравнительно просто определить форму сейсмических лучей. В однородной изотропной среде, где V=const сейсмические лучи представлены прямыми линиями. В неоднородных изотропных средах V=grad, т.е. в средах, упругие константы которых зависят от координат пространства, форма сейсмического луча существенно усложняется, поскольку они становятся криволинейными. Поиск траектории таких лучей осуществляется на основе принципа Ферма и математически сводится к решению вариационной задачи на определение минимума времени пробега волны между двумя точками А и В:

t = 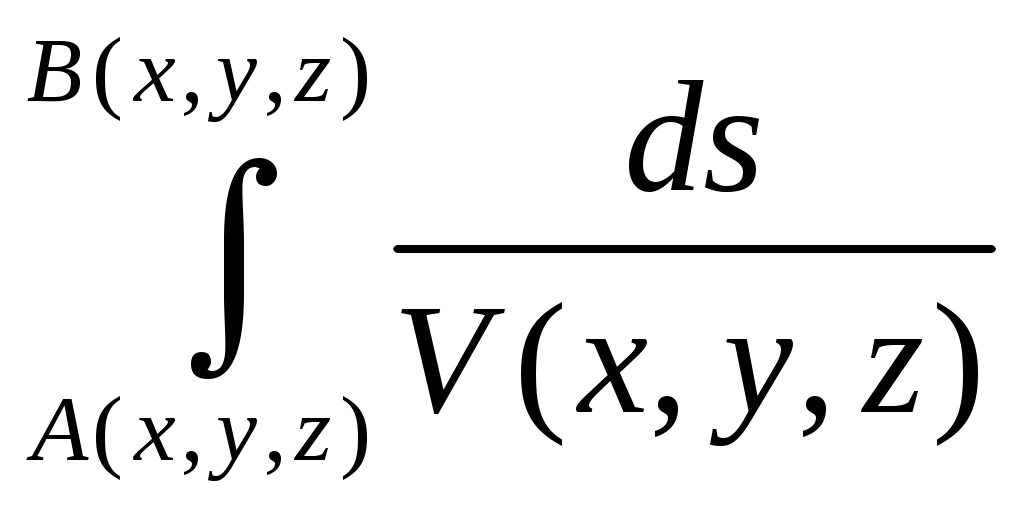, (1.17)

где ds – элемент длины дуги, соединяющей точки А и В.

В соответствии с принципом Гюйгенса – любая точка, взятая на поверхности изохроны, соответствующей фронту волны, является элементарным источником колебаний. Принцип Гюйгенса в простейшей форме можно использовать для определения положения фронтов волн для разных моментов времени. Пусть фронт волны в некоторый момент времени t=t п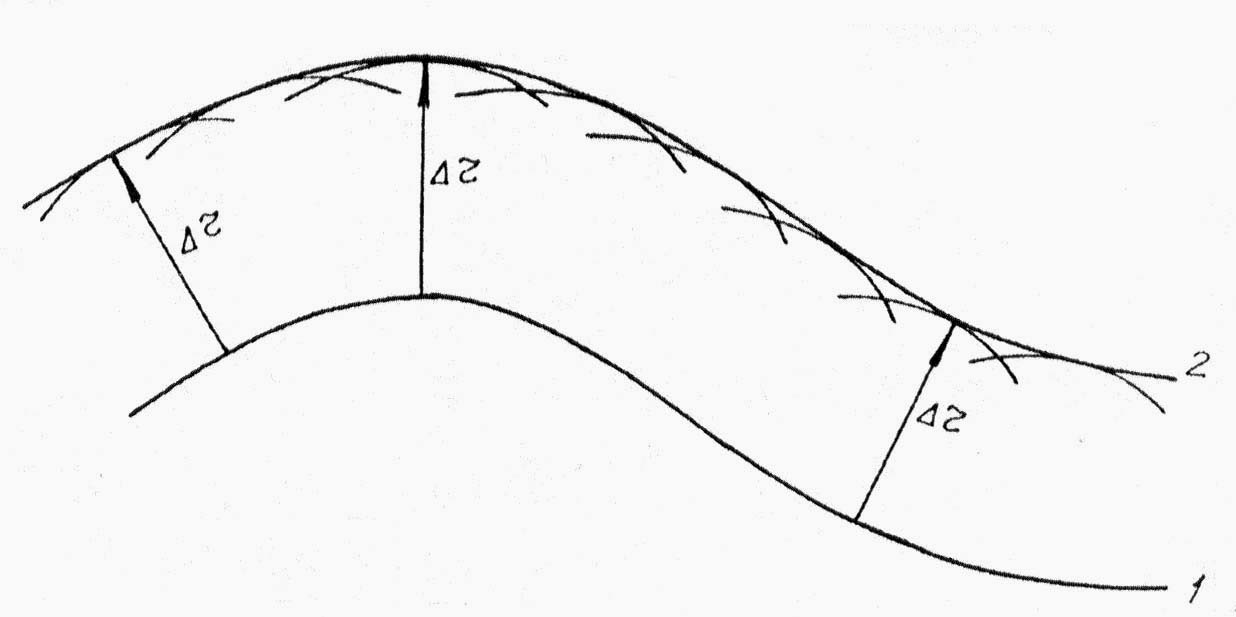редставлен линией 1 (рис.1.9). Согласно этому принципу, форма фронта волны 2 в момент времени t = t +∆tбудет представлять собой огибающую к элементарным фронтам волн радиуса ∆r=∆t .

Р ис.1.9. Схема построения фронта волны: 1- положение исходной изохронны на 1 момент времени t ; 2 – положение фронта волны в момент времени t

На этом принципе основана группа способов решения прямых и обратных задач сейсморазведки, условно называемая методом полей времен, который широко применяется для интерпретации волновых полей.

Френель на основе принципа Гюйгенса первым сформулировал количественный подход к оценке размеров части среды, активно участвующей в передаче волны от источника к точке наблюдения. Если задать плоскость и построить линию перпендикулярную к ней и соединяющую источник О и точку приема М, то на этой плоскости можно построить зоны Френеля (рис. 1.10) – систему концентрических колец такой ширины, чтобы при переходе от внутреннего контура к внешнему, время прихода колебаний в точку М изменялось бы на половину периода.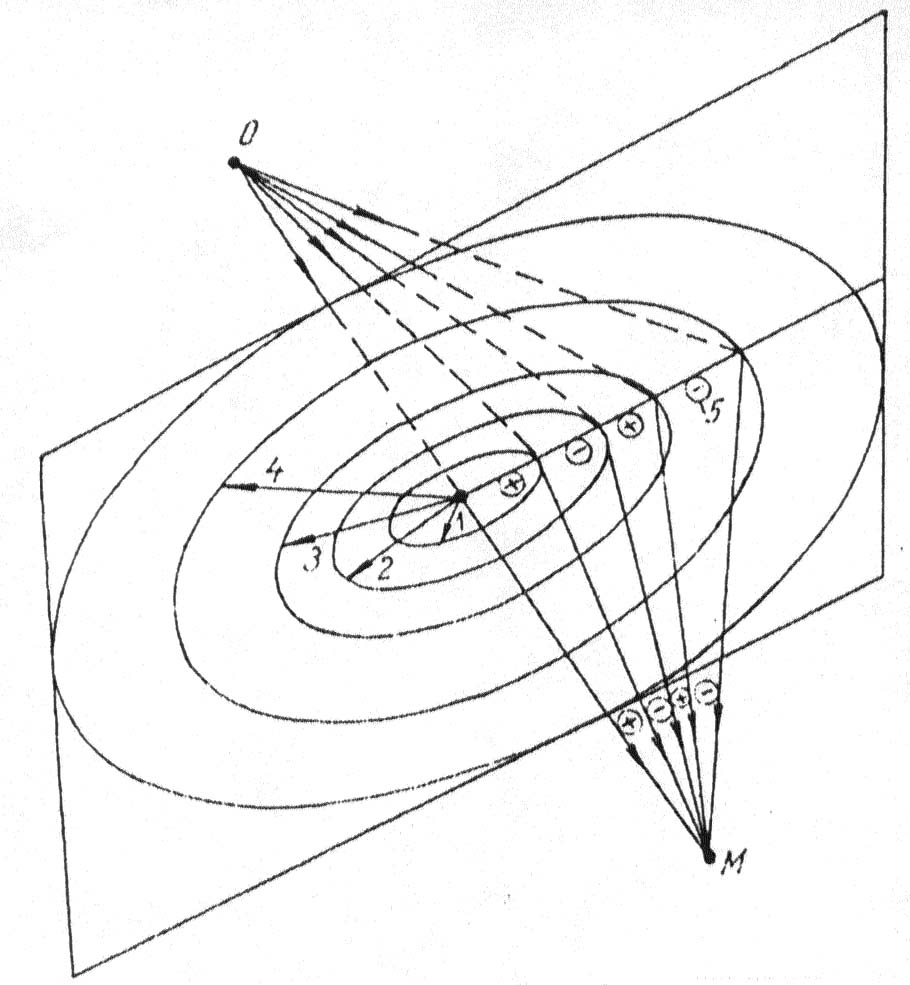



Рис.1.10. Схема расположения зон Френеля: 1, 2, 3, 4 – радиусы зон;

5 – знак зон Френеля ( «+» или «–»)
Таким образом, можно считать, что каждая из зон порождает в точке М знакопеременные колебания. При сложении эффектов от всех зон получается знакопеременный ряд с постоянно убывающими по абсолютной величине членами. Структура этого ряда близка к бесконечной геометрической прогрессии, сумма которой приблизительно равна половине величины первого слагаемого. Поэтому результирующий эффект в точке М будет равен примерно половине воздействия от первой (центральной) зоны Френеля. Радиус круга, площадь которого равна половине площади первой зоны Френеля, будет определяться формулой

R = , (1.18)

где r – расстояние от источника до рассматриваемой плоскости; l – расстояние от рассматриваемой плоскости до точки наблюдения; λ – преобладающая длина волны.

Максимального значения величина R в однородной среде достигает в середине пути от источника до приемника:

R = . (1.19)

Именно эта формула позволяет оценить максимальный размер зоны, формирующей передачу энергии относительно плоскости отражения.
1.5. Поверхностные волны

В однородной безграничной среде, как было рассмотрено выше, могут распространяться продольные и поперечные волны. Они распространяются по всему объему среды и поэтому называются объемными волнами.

При наличии поверхности, которая разделяет пространство на два полупространства – нижнее, заполненное однородной упругой средой, и верхнее – воздухом, то вдоль границы раздела «земля-воздух» распространяется поверхностная волна Релея. При распространении волны Релея одновременно происходят деформации и объема и формы. По этой причине траектории движения частиц представляют эллипсы, у которых отношение горизонтальной и вертикальной осей приблизительно равно 0,7. Такие волны очень быстро затухают с глубиной, т.е. они фактически распространяются вдоль некоторого слоя, прилегающего к границе «земля-воздух», причем амплитуды смещения убывают с глубиной примерно по экспоненциальному закону. Скорость распространения волны Релея примерно равна V , где V - скорость поперечной волны в нижнем полупространстве.

В сейсморазведке поверхностные волны релеевского типа являются помехами, которые мешают регистрировать отраженные и другие полезные волны (рис.1.11). Их интенсивность, если не принять ряд специальных мер (группирование сейсмоприемников, частотную фильтрацию, процедуры обработки и т.д.), может во много раз превышать интенсивность полезных волн. Поэтому изучение их характеристик необходимо для успешной борьбы с ними.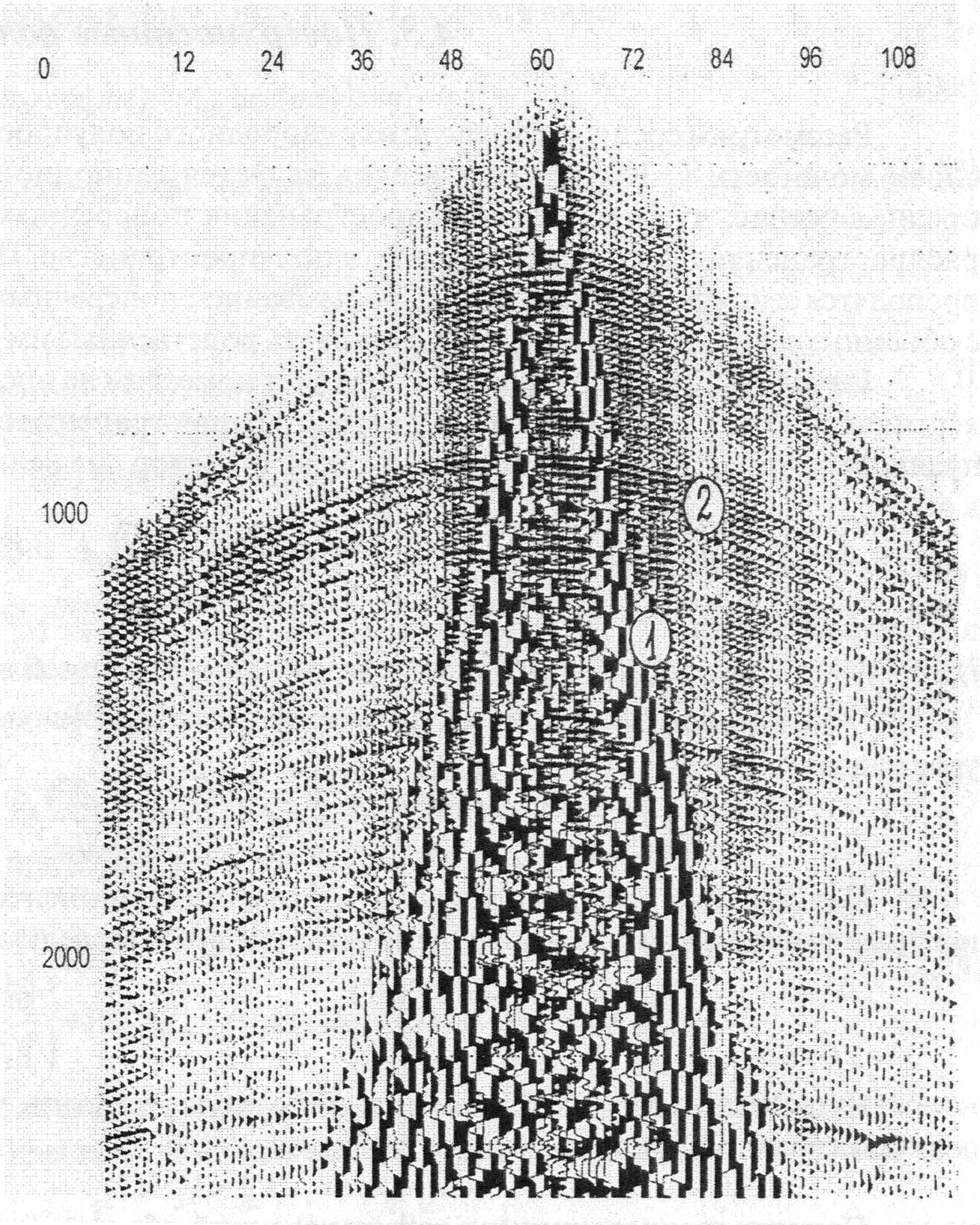



Рис. 1.11. Типичный пример записи сейсмограммы МОВ: 1 – цуг колебаний волн помех релеевского типа; 2 – отраженные волны

Другим типом поверхностных волн являются волны Лява. Она может возникнуть, когда на упругом полупространстве лежит тонкий слой, скорость поперечной волны в котором V значительно меньше скорости V в упругом полупространстве (V «V ). Волны Лява представляют суммарные колебания, образованные сложением смещений поперечной волны, многократно отразившейся от верхней и нижней границ тонкого пласта. Скорость этих волн зависит от частоты (длины) волны и изменяется в пределах: от 0.9 V - для очень коротких волн до 0,9 V - для очень длинных волн. По мере распространения волны в нижний пласт её амплитуда быстро убывает. Как и волна Релея относится к помехам.

При взрывах в шурфах и скважинах в воздухе возникают и распространяются звуковые волны. Они являются продольными волнами и характеризуются скоростью около 340 .
1.6. Распространение сейсмических волн

в не абсолютно упругих средах
Все реальные среды можно рассматривать как абсолютно упругие, только в некотором приближении, позволяющем более или менее точно описать изменения параметров волны при прохождении сравнительно небольших расстояний. Экспериментальные исследования процесса распространения упругих волн на большие расстояния от источника показали их более сильное ослабление, чем это вытекает из расчетов, основанных на формулах для абсолютно упругих сред. Изменение интенсивности волн сопровождается изменением формы трассы записи. Эти явления могут быть объяснены, если предположить существование некоторого механизма поглощения энергии сейсмических волн путем перехода её в другие виды, например в тепловую. Среды, в которых происходит такое преобразование энергии упругих колебаний, принято называть поглощающими.

Эффект поглощения амплитуды сейсмической волны описывается зависимостью: А(r)= A , (1.20)

где A (r) – амплитуда волны в расчетной точке; A - амплитуда волны в точке возбуждения; r - расстояние от источника до расчетной точки; - амплитудный коэффициент поглощения; - круговая частота колебаний. Из этой формулы видно, что коэффициент , определяющий интенсивность ослабления волны с расстоянием, зависит от частоты. Разные теории приводят к различным формам этой зависимости.

Согласно теории вязкого трения: , где - коэффициент поглощения, зависящий от свойств упругой среды. Единицы измерения - .

Теория упругого последействия приводит к линейной зависимости коэффициента от частоты: ( ) = , где - постоянная поглощения.

В настоящее время отсутствуют устоявшиеся взгляды на эти вопросы. Однако практика подтверждает, что в большинстве случаев для горных пород зависимость коэффициента поглощения от частоты близка к зависимости на рисунке 1.12, промежуточной между двумя выше названными. Во всех случаях коэффициент поглощения 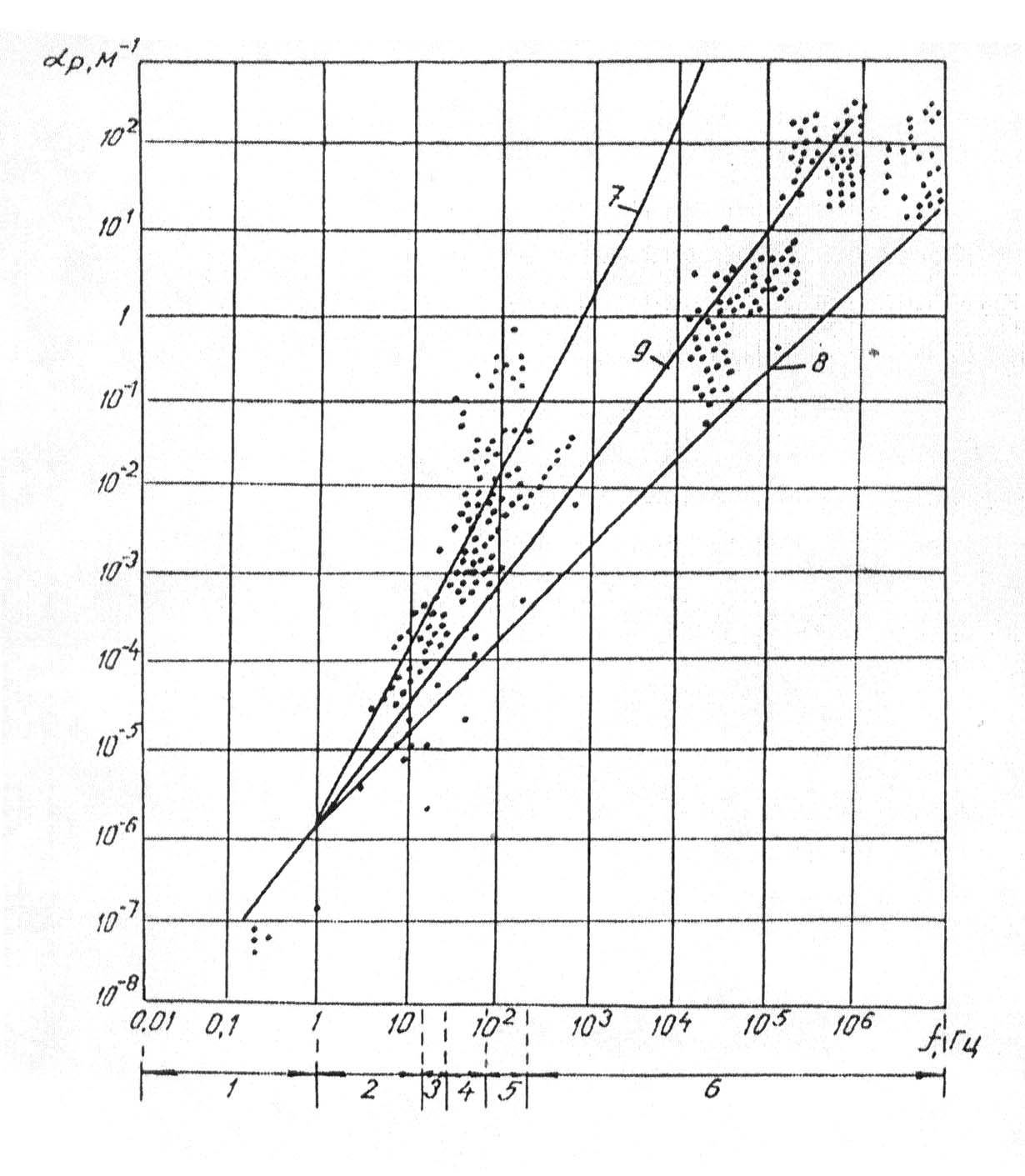является возрастающей функцией частоты.




Рис.1.12. Обобщенные экспериментальные данные о зависимости коэффициента поглощения для пород различного литологического состава от частоты.

Области частот, используемые при: 1 – сейсмологии; 2 – глубинных сейсмических зондированиях; 3, 4. 5 – низко-, средне- и высокочастотной сейсмораз-ке; 6 – лабораторных исследованиях.

Графики, проведенные в соответствии с теорией: 7 – вязкого трения; 8 – упругого последействия; 9 – осреднения

Из графиков следует, что по мере увеличения коэффициента поглощения происходит избирательное ослабление частоты волны (сначала низкие, затем средние и высокие частоты). Это обстоятельство приводит к изменению формы записи волны по мере её удаления от источника.


2. Отражение и преломление на границе раздела двух сред

2.1. Образование вторичных волн

Рассмотрим случай, когда существуют два пласта Iи II большой мощности, разделенные плоской границей раздела R (рис. 2.1). Пусть скорости продольных

и поперечных волн в пласте I равны

Р Р S Р V и V соответственно, в пласте II

I скорости этих волн примем равны-

R ми V и V . Предположим, что в пласте Iраспространяется упругая

II Р S Р волна, которую назовем падающей.

Последняя, в зависимости от типа

Рис.2.1.Образование вторичных волн связанных с ней деформаций может быть продольной или попе- речной. Рассмотрим случай, когда продольная падающая волна Р достигает границы раздела R, где происходит её отражение и преломление. За счет энергии падающей волны образуются вторичные волны. К их числу относятся отраженные волны – продольная Р и поперечная Р S , распространяющиеся в пределах пластаI и проходящие волны (в пласте II) - также продольная Р и поперечная Р S . Таким образом на границе раздела двух сред каждая падающая волна (согласно принципа Гюйгенса) возбуждает четыре вторичные волны - Р , Р S , Р , Р S . Две из них имеют тот же тип, что и падающая и называются монотипными. Две другие меняют свой тип на границе раздела и поэтому называются обменными волнами. В рассматриваемом случае монотипные волны : отраженная продольная - Р и проходящая продольная Р , обменные – отраженная поперечная - Р S и проходящая поперечная - Р S . Основные типы волн на которых основываются методы сейсморазведки это - отраженная продольная волна - Р и проходящая продольная - Р .