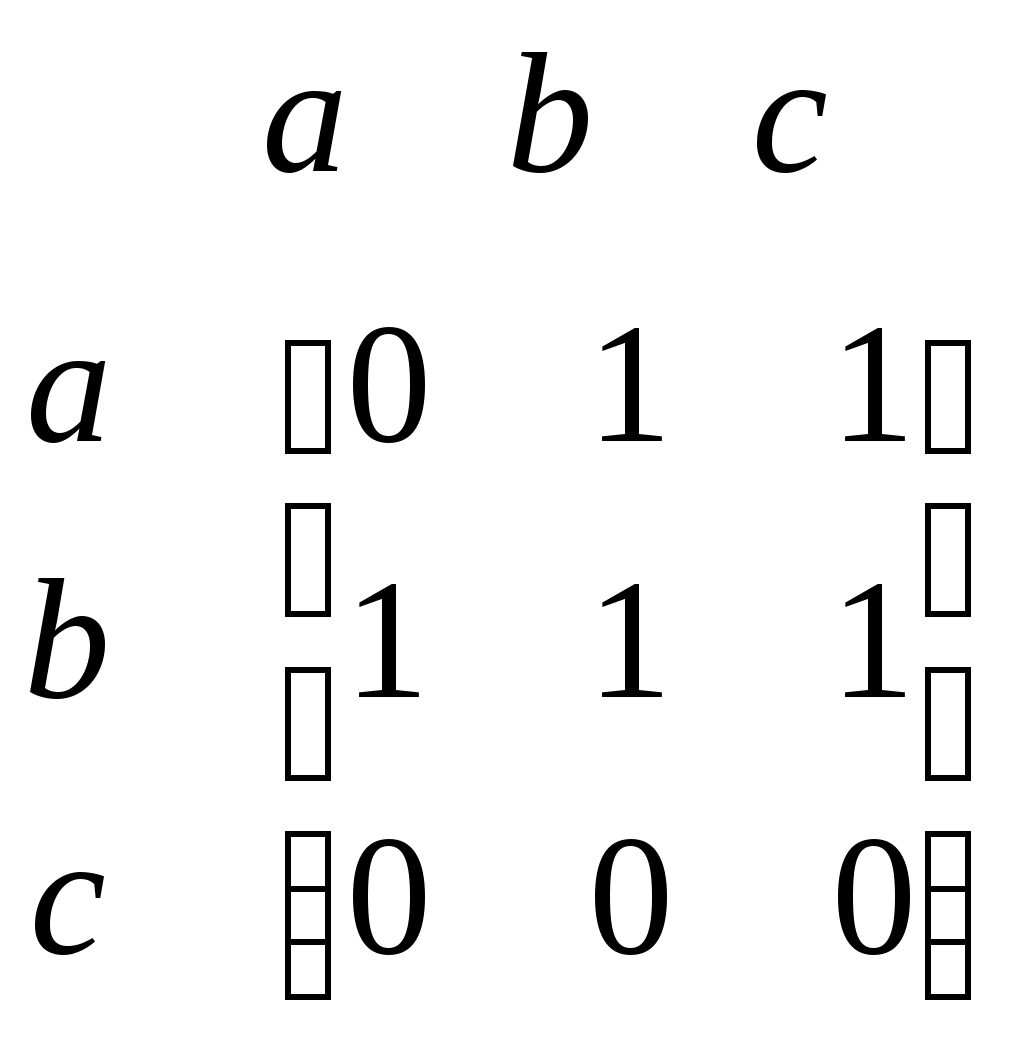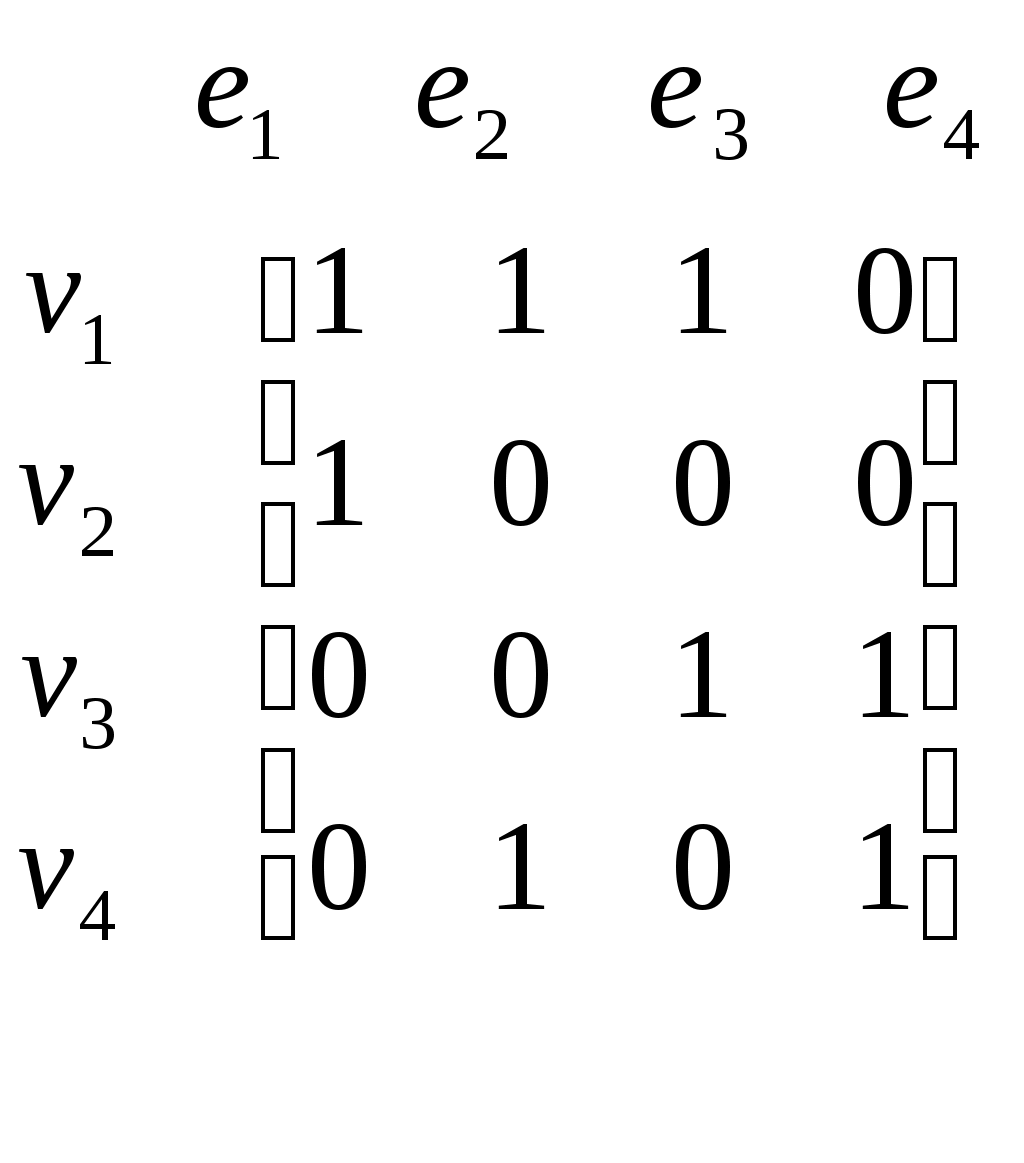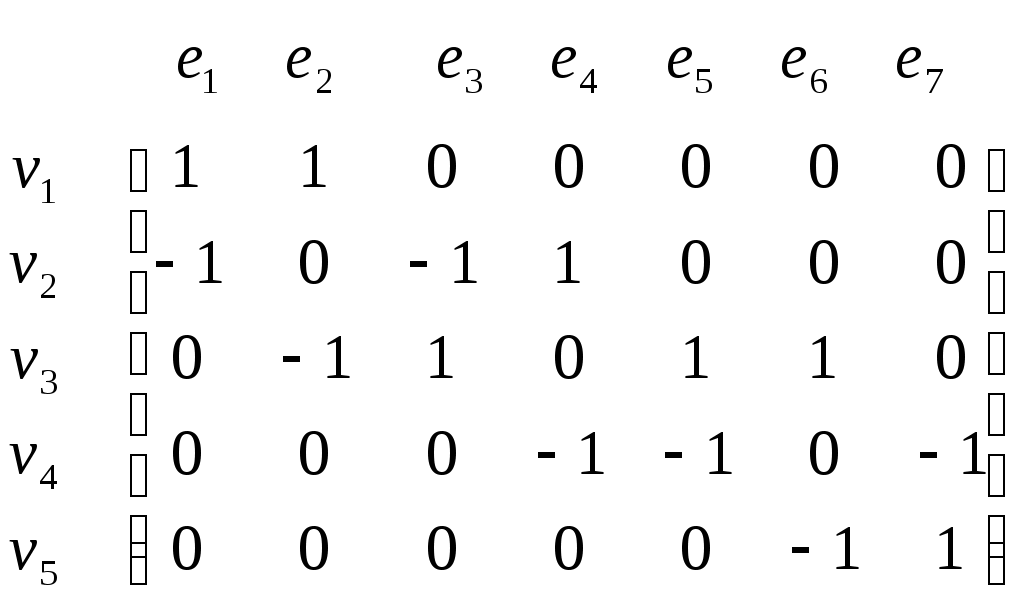Введение в теорию графов.
При использовании понятия «граф» в математике чаще всего имеют в виду графическое задание связей между объектами произвольной природы. Например, можно говорить о графическом способе задания связей между атомами в молекуле вещества; структура некоторого подразделения или карта автомобильных дорог представляется графом,
Дадим определение графа. Конечное множество 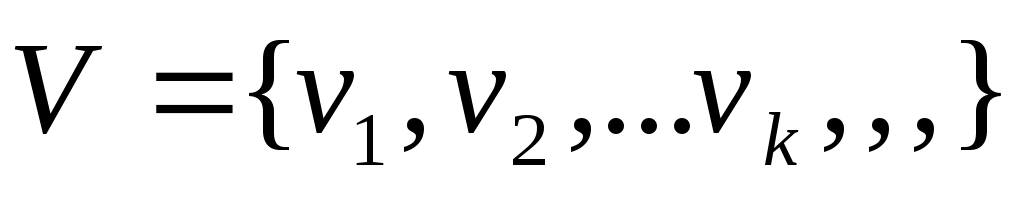 и множество и множество 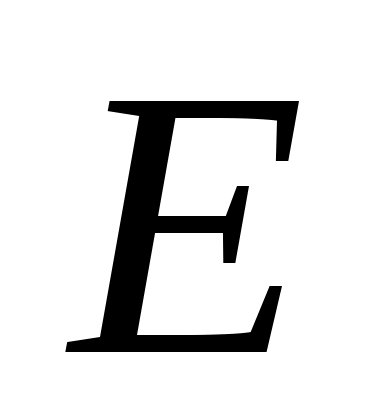 пар объектов вида пар объектов вида 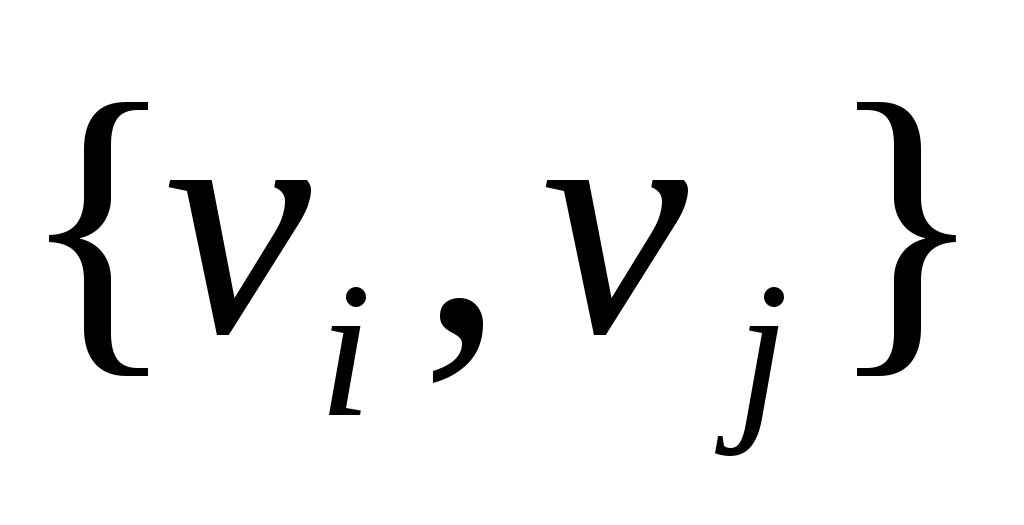 или или 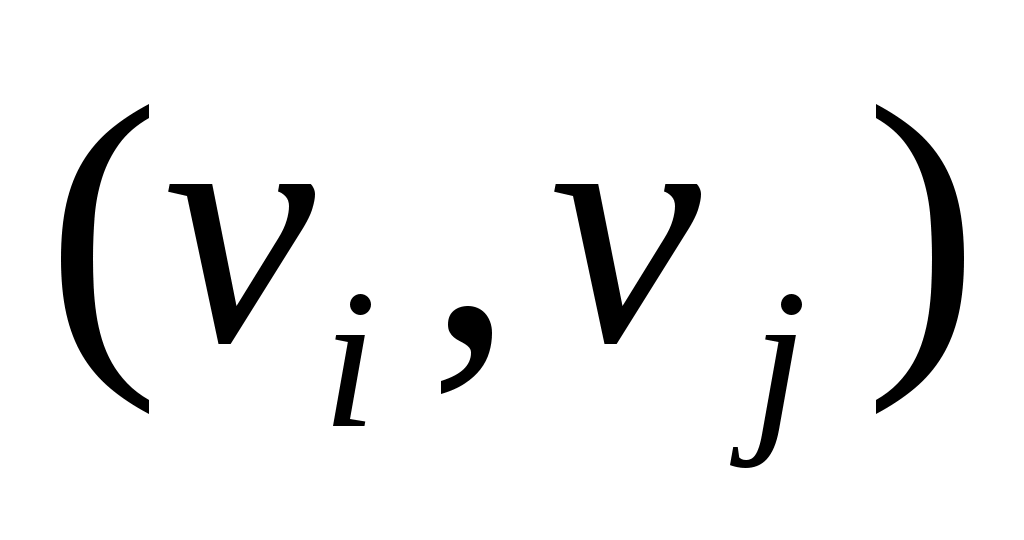 из множества из множества 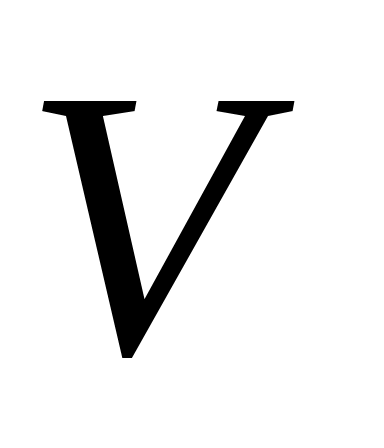 называется графом. Будем обозначать граф называется графом. Будем обозначать граф  . Множество . Множество 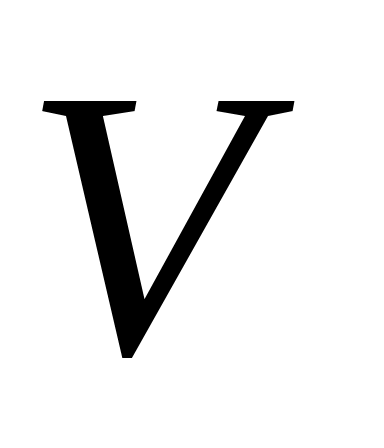 называется множеством вершин графа. Элементы множества называется множеством вершин графа. Элементы множества 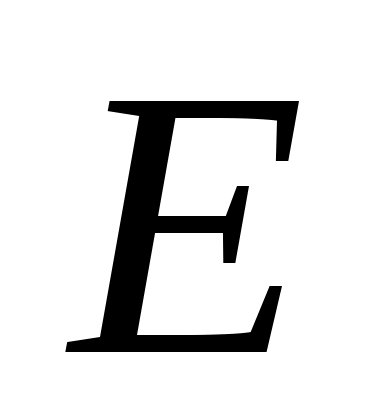 вида вида 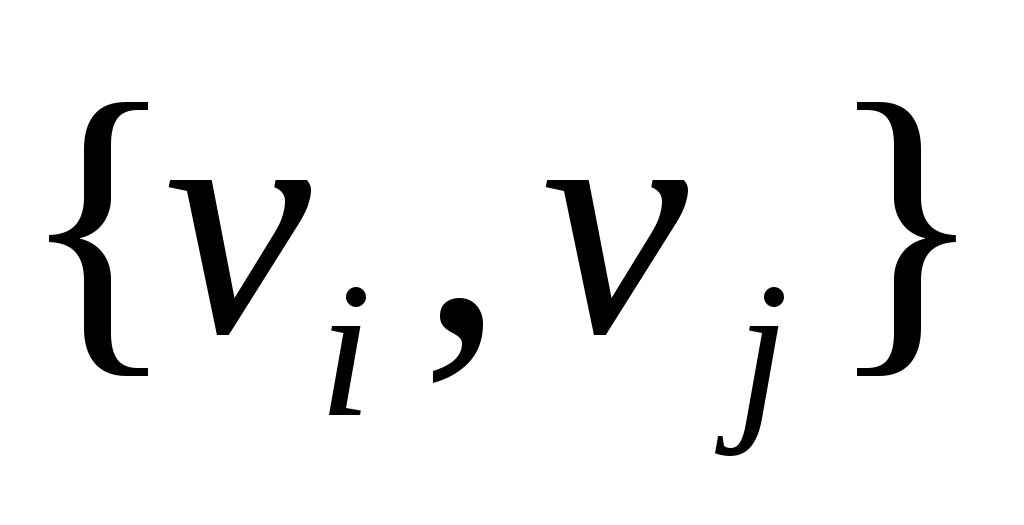 называются ребрами графа. Ребро – это неупорядоченная пара вершин, т.е. неважно, какая из вершин в паре является начальной, а какая конечной, поэтому мы и взяли пару в фигурные скобки. Элементы множества называются ребрами графа. Ребро – это неупорядоченная пара вершин, т.е. неважно, какая из вершин в паре является начальной, а какая конечной, поэтому мы и взяли пару в фигурные скобки. Элементы множества 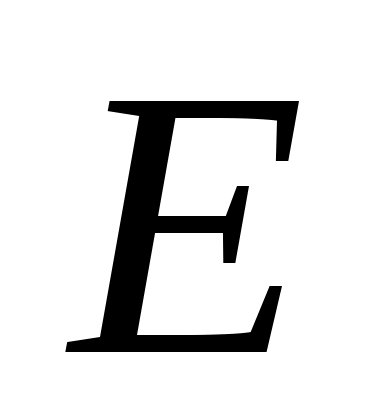 вида вида 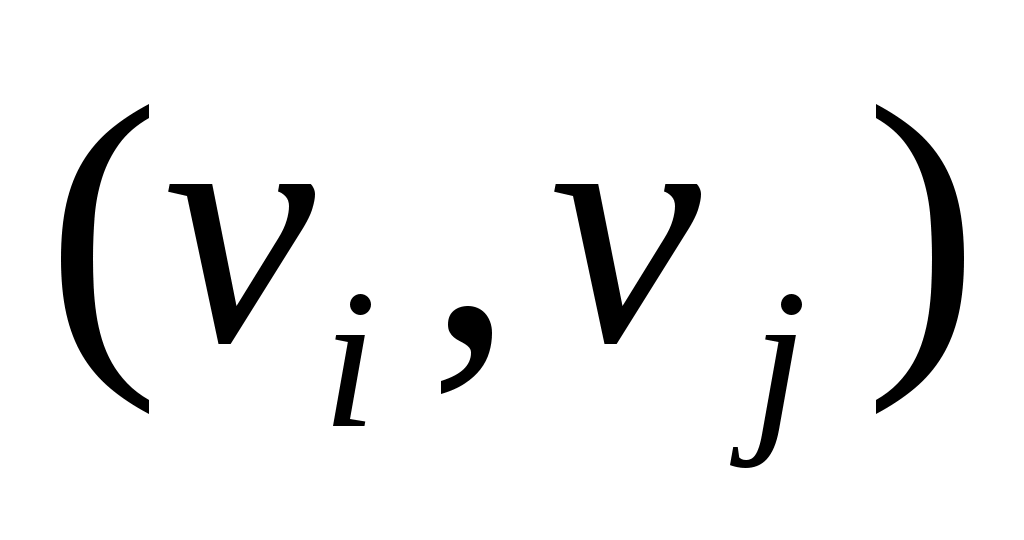 называются дугами графа. Дуга – это упорядоченная пара вершин, указывается начальная и конечная вершина пары, пара берется в круглые скобки. Если в графе начальная и конечная вершины ребра (или дуги) совпадают, то говорят, что в графе имеется петля. Если вершины соединены несколькими ребрами (или дугами), то такие ребра (дуги) называются кратными. Граф, в котором есть кратные ребра (дуги) называется мультиграфом. Псевдографом называется граф, имеющий и петли и кратные ребра (дуги). называются дугами графа. Дуга – это упорядоченная пара вершин, указывается начальная и конечная вершина пары, пара берется в круглые скобки. Если в графе начальная и конечная вершины ребра (или дуги) совпадают, то говорят, что в графе имеется петля. Если вершины соединены несколькими ребрами (или дугами), то такие ребра (дуги) называются кратными. Граф, в котором есть кратные ребра (дуги) называется мультиграфом. Псевдографом называется граф, имеющий и петли и кратные ребра (дуги).
Граф, состоящий из вершин и соединяющих их ребер, называется неориентированным графом. Неориентированный граф, не содержащий петель и кратных ребер, называется простым. Граф, состоящий из вершин и дуг – ориентированным или орграфом. Графы, содержащие и дуги и ребра, называются смешанными. При графическом изображении графа вершины обозначаются точками, а ребра (дуги) – линиями, соединяющие соответствующие вершины, для орграфа на дуге ставится стрелка, задающая направление от начальной вершины к конечной.
 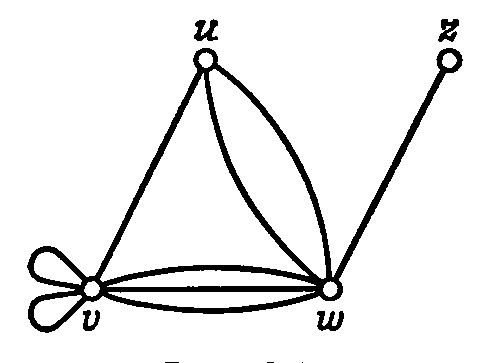 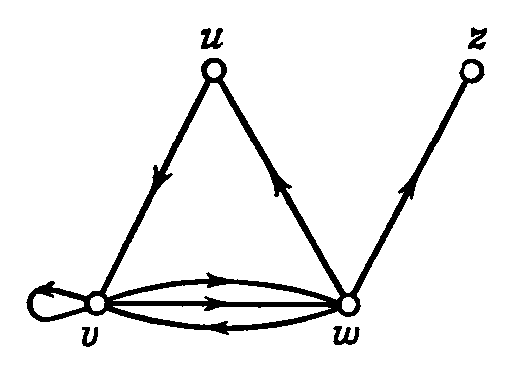
б. в.
Рис. 1.
На рис. 1 изображены:
а – простой граф;
б – неориентированный псевдограф;
в - ориентированный псевдограф;
Если 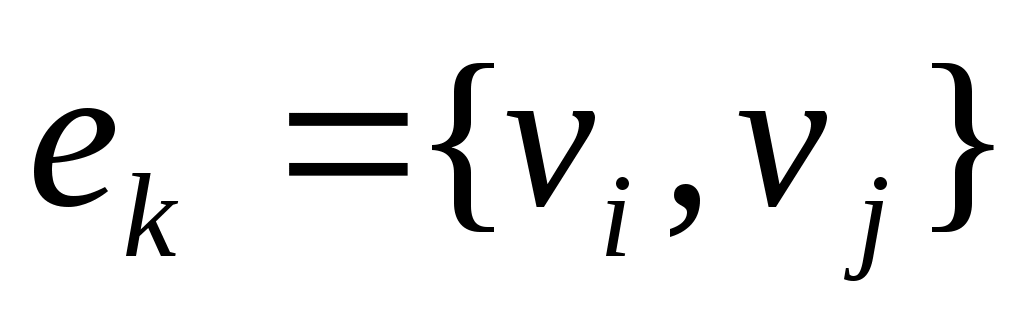 - ребро графа, то вершины - ребро графа, то вершины 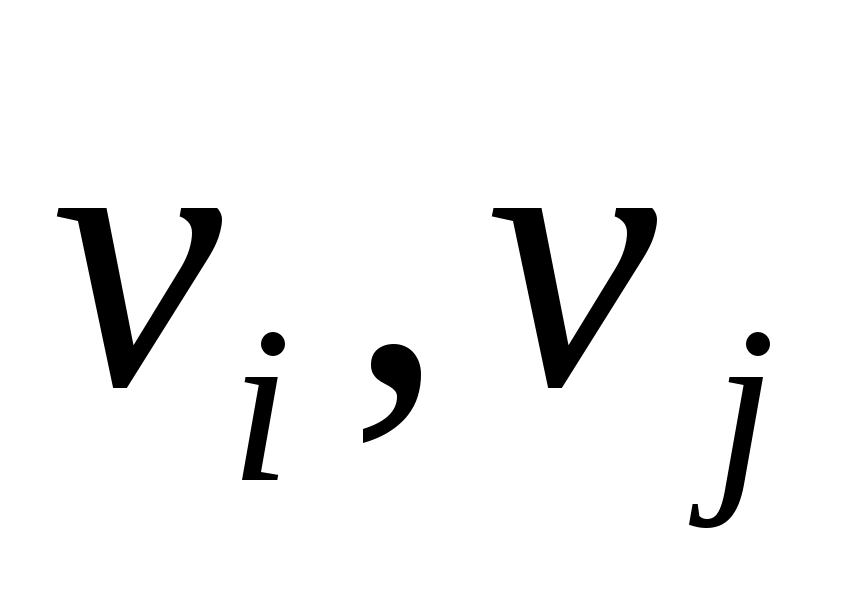 называются концами ребра называются концами ребра 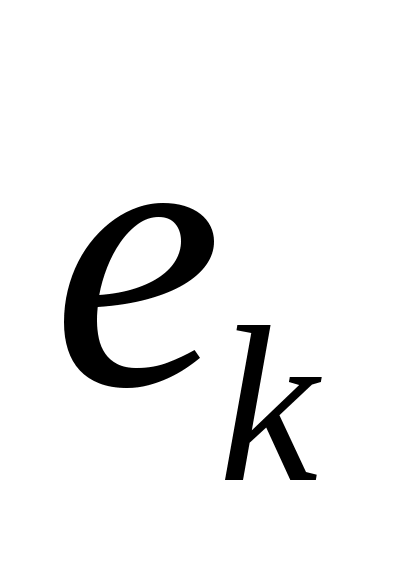 , в этом случае также говорят, что ребро , в этом случае также говорят, что ребро 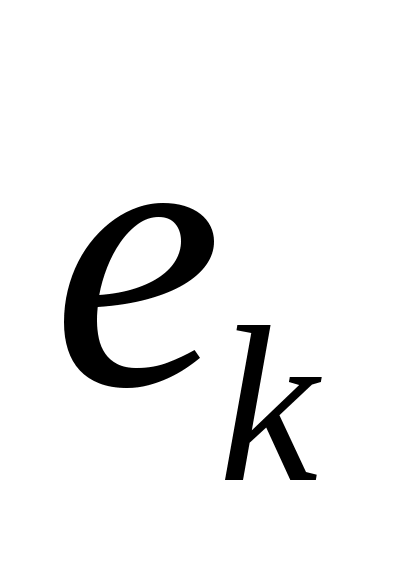 соединяет вершины соединяет вершины 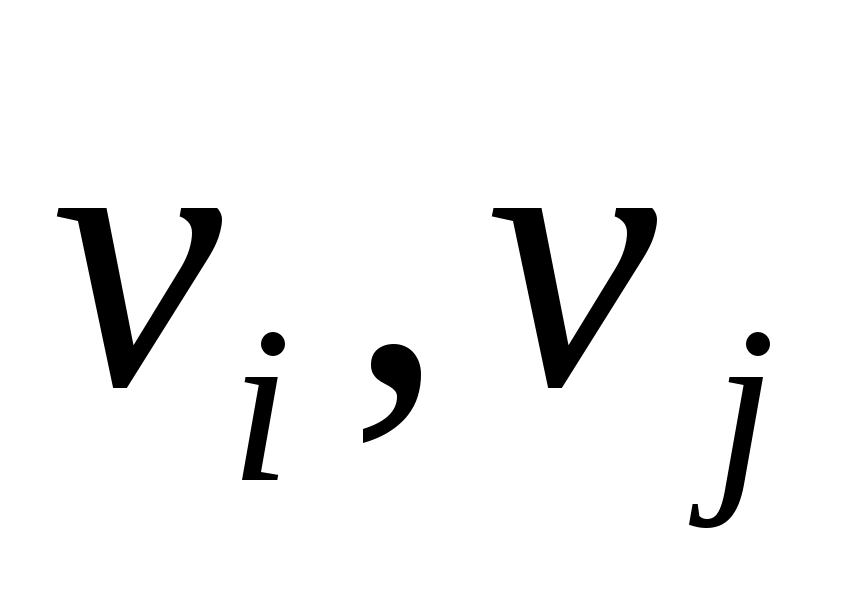 . .
Если  - дуга орграфа, то вершина - дуга орграфа, то вершина  называется началом, а вершина называется началом, а вершина 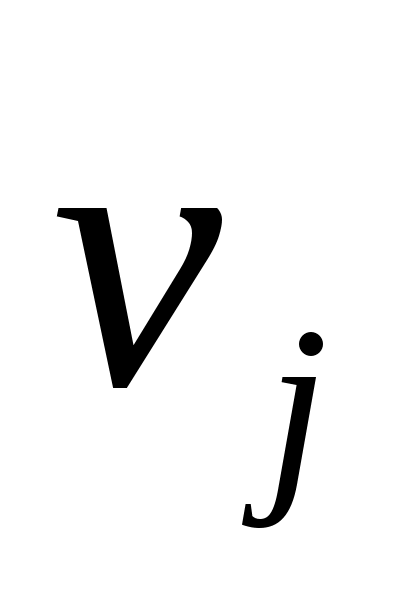 - концом дуги - концом дуги 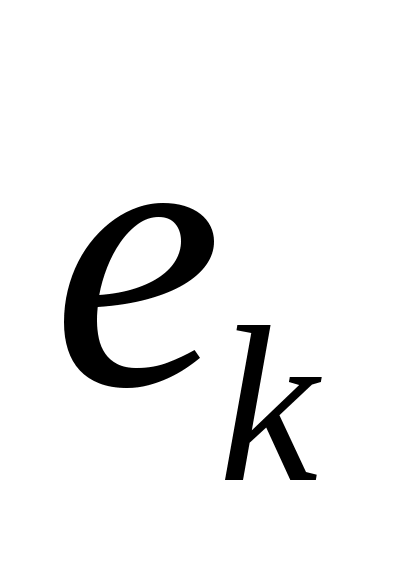 , при этом говорят, что дуга , при этом говорят, что дуга 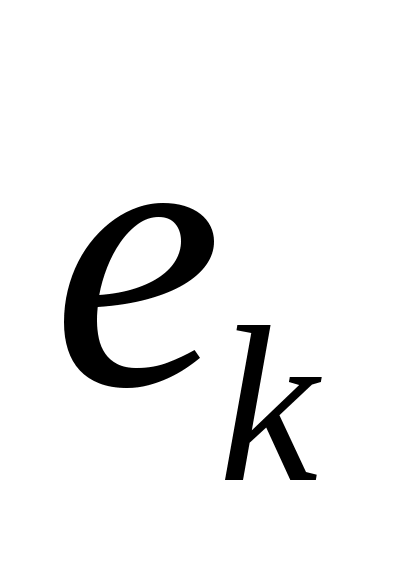 исходит из вершины исходит из вершины  и заходит в вершину и заходит в вершину 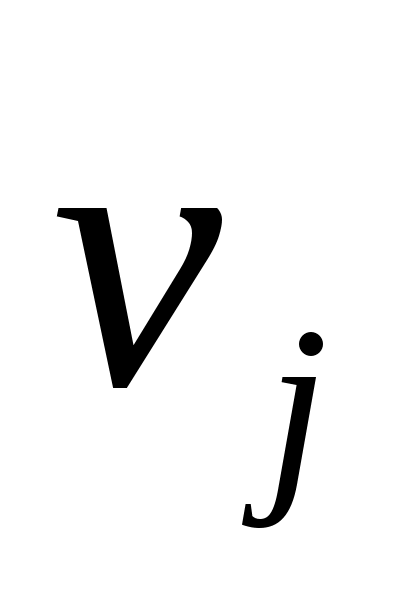 . .
Если ребро (дуга) 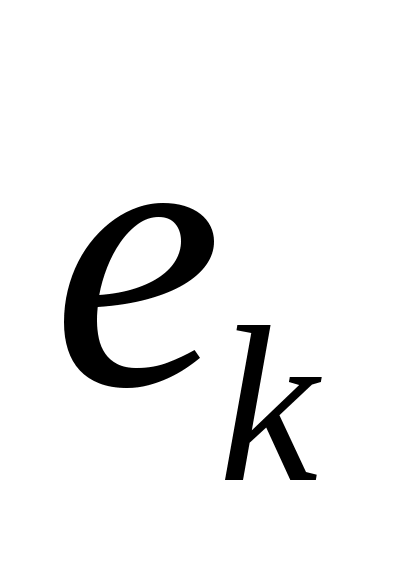 соединяет вершины соединяет вершины 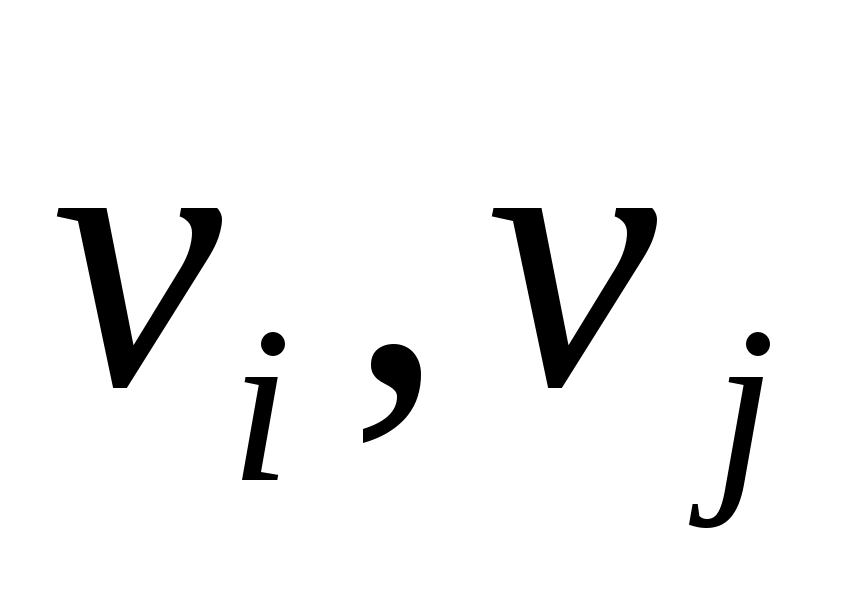 , то говорят, что ребро (дуга) , то говорят, что ребро (дуга) 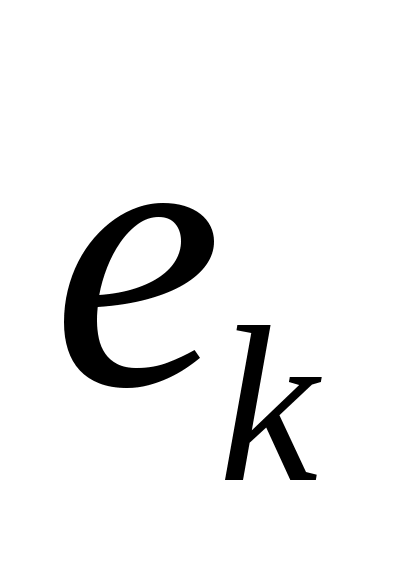 инцидентно вершинам инцидентно вершинам 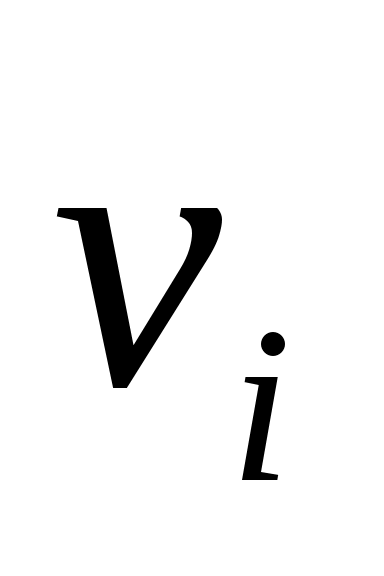 и и 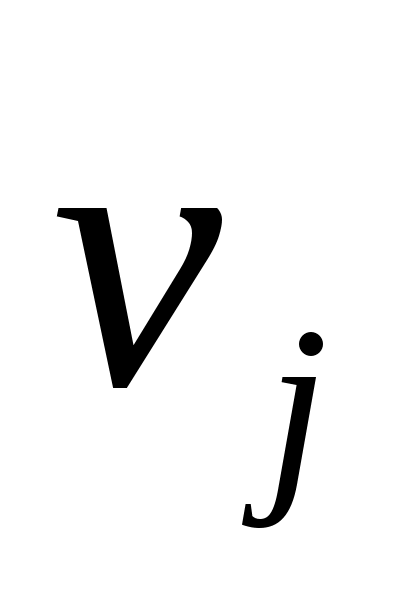 или вершины или вершины 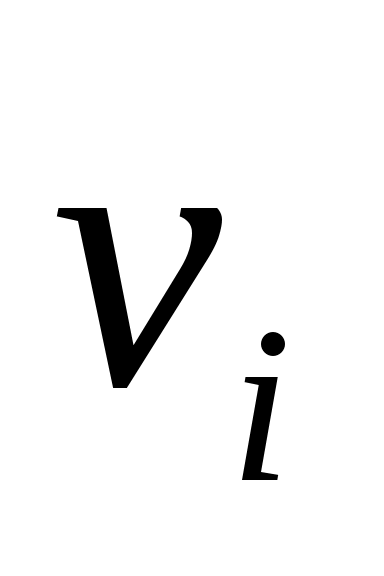 и и 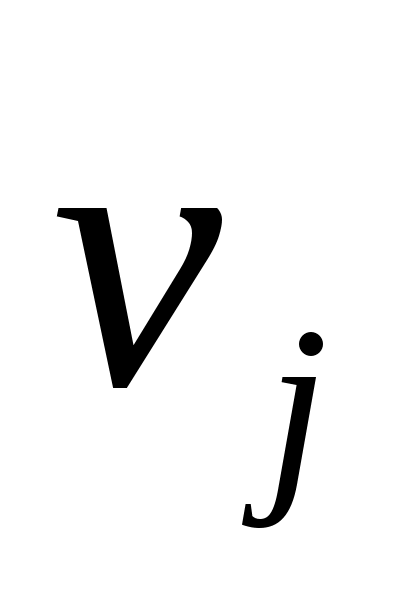 инцидентны ребру (дуге) инцидентны ребру (дуге) 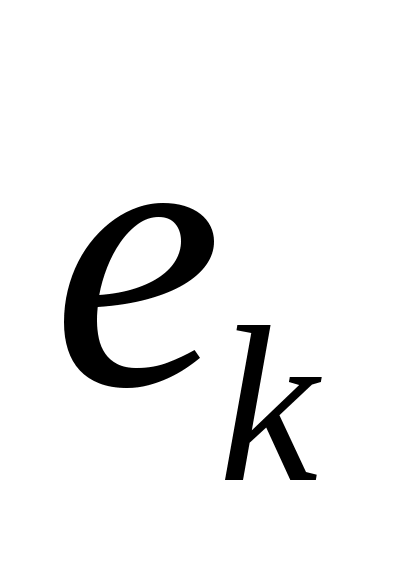 . .
Вершины графа 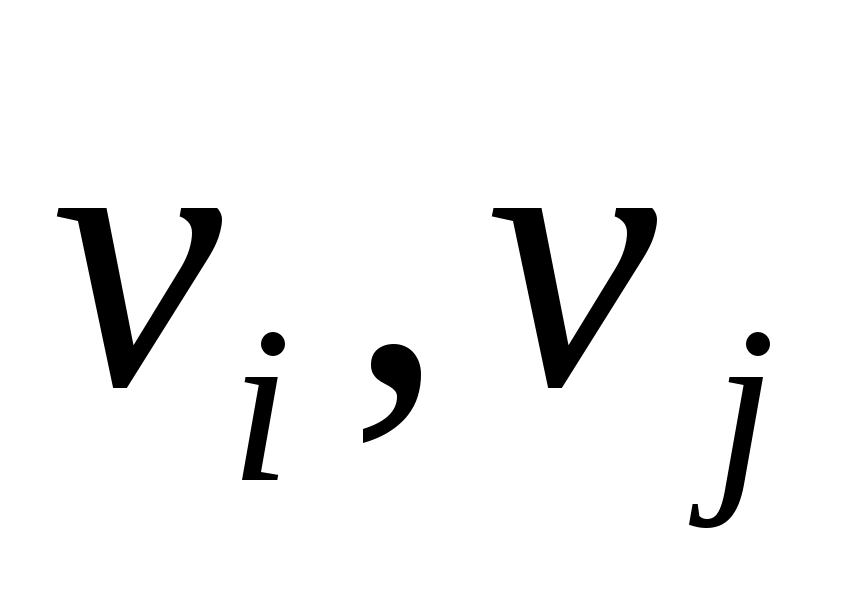 , соединенные хотя бы одним ребром, называются смежными. Простой граф, в котором любые две вершины смежные, называется полным графом. Полный граф с n вершинами обычно обозначается как , соединенные хотя бы одним ребром, называются смежными. Простой граф, в котором любые две вершины смежные, называется полным графом. Полный граф с n вершинами обычно обозначается как  . Ниже на рис.2 приведен граф . Ниже на рис.2 приведен граф 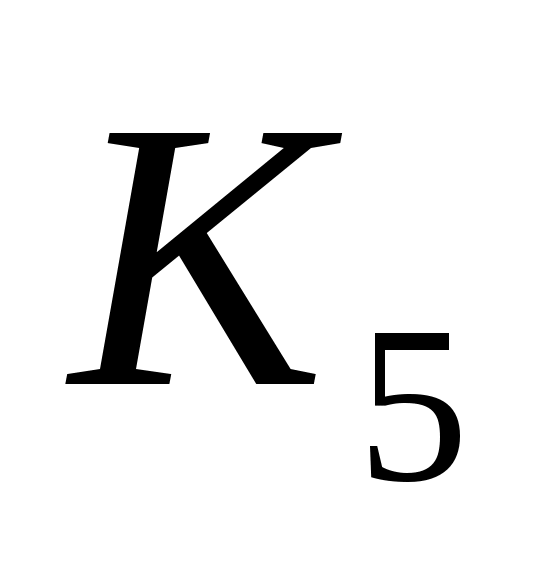 . .

Рис.2.
Вершина графа, не смежная ни с какой другой вершиной этого графа, называется изолированной.
Два ребра называются смежными, если они имеют общую вершину.
Степенью вершины vнеориентированного графа, обозначаемой 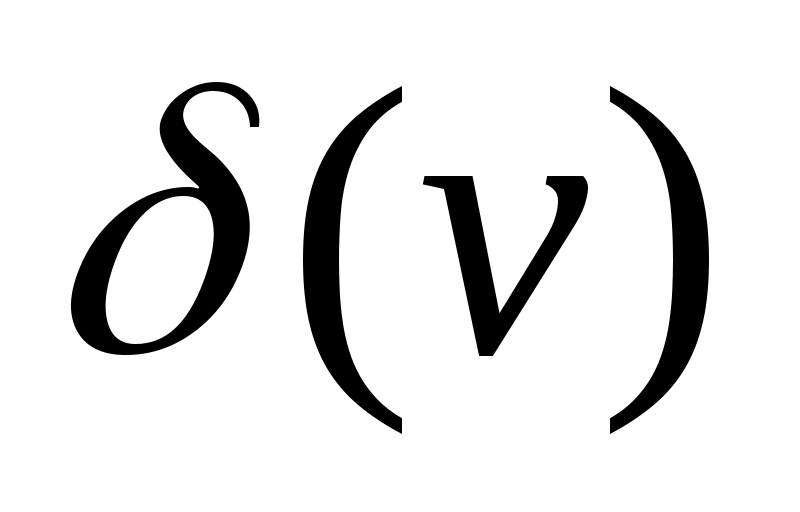 или deg(v) называется количество ребер, инцидентных этой вершине. Вершина степени 0 называется изолированной, степени 1 – висячей. Петля учитывается дважды. Например, для псевдографа, изображенного на рисунке 1. б, z – висячая вершина, или deg(v) называется количество ребер, инцидентных этой вершине. Вершина степени 0 называется изолированной, степени 1 – висячей. Петля учитывается дважды. Например, для псевдографа, изображенного на рисунке 1. б, z – висячая вершина, 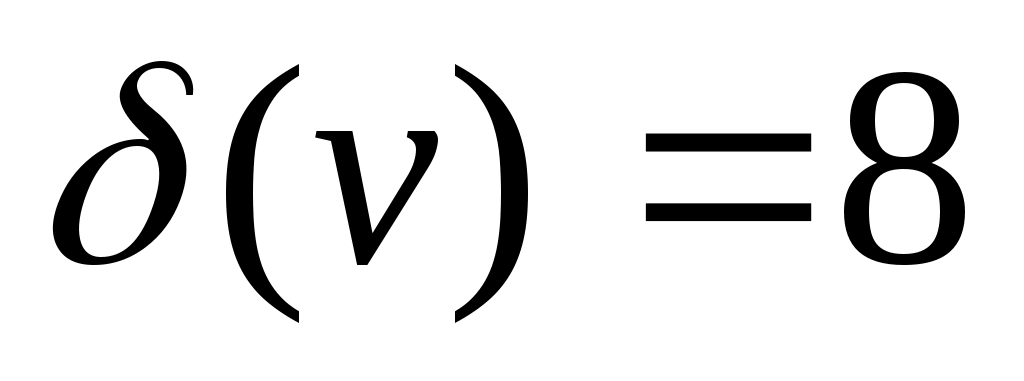 , ,  . .
Если степени всех вершин графа равны k , то граф называется регулярным степени k.

Рис. 3.
На рис. 3 изображен граф, у которого степень каждой вершины равна 3 (кубический граф).
Полустепенью выхода (исхода) вершины v в орграфе D называется число дуг орграфа, исходящих из вершины v. Например, для орграфа на рис. 1. в дуг орграфа, исходящих из вершины v. Например, для орграфа на рис. 1. в 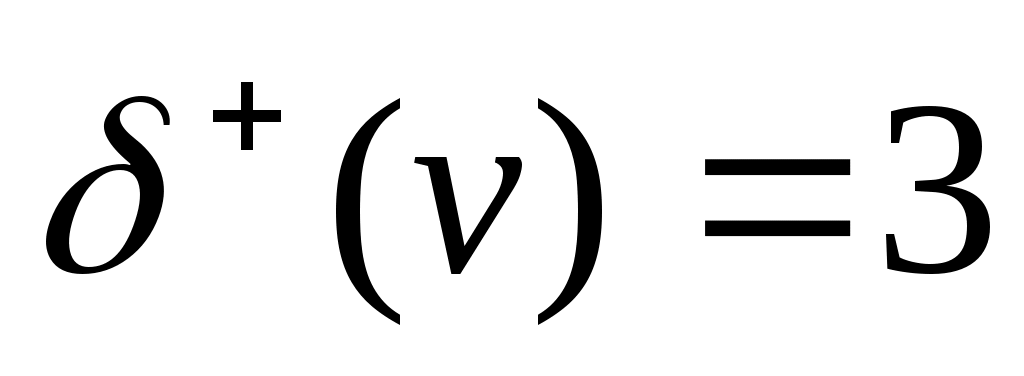 , , 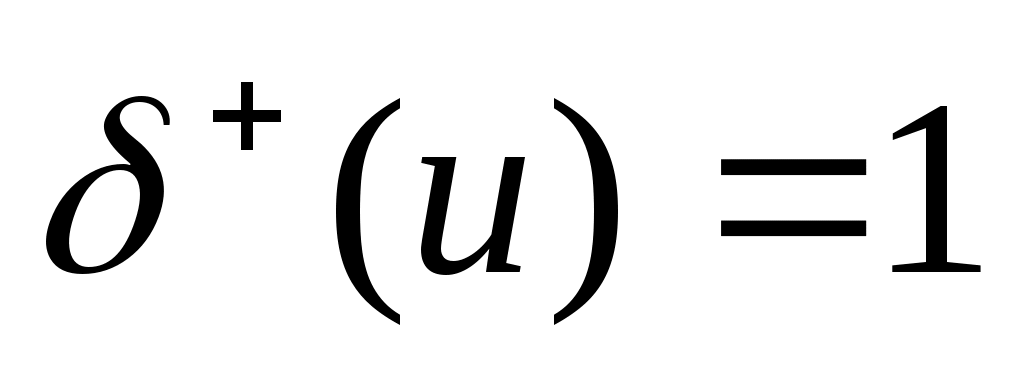 . Если . Если  , то вершина v называется стоком. , то вершина v называется стоком.
Полустепенью входа (захода) вершины v в орграфе D называется число дуг орграфа, заходящих в вершину v. Например, для орграфа на рис. 1.в дуг орграфа, заходящих в вершину v. Например, для орграфа на рис. 1.в  , , 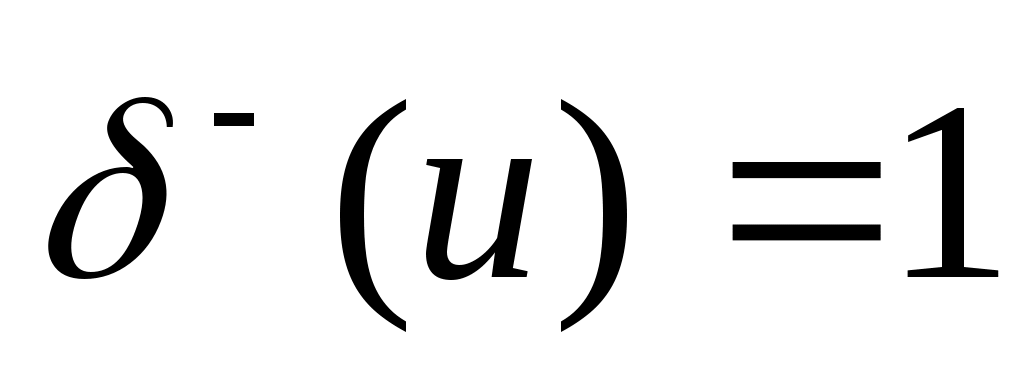 . В случае ориентированного псевдографа вклад каждой петли, инцидентной некоторой вершине v , равен 1, как для . В случае ориентированного псевдографа вклад каждой петли, инцидентной некоторой вершине v , равен 1, как для  , так и для , так и для  . Если . Если 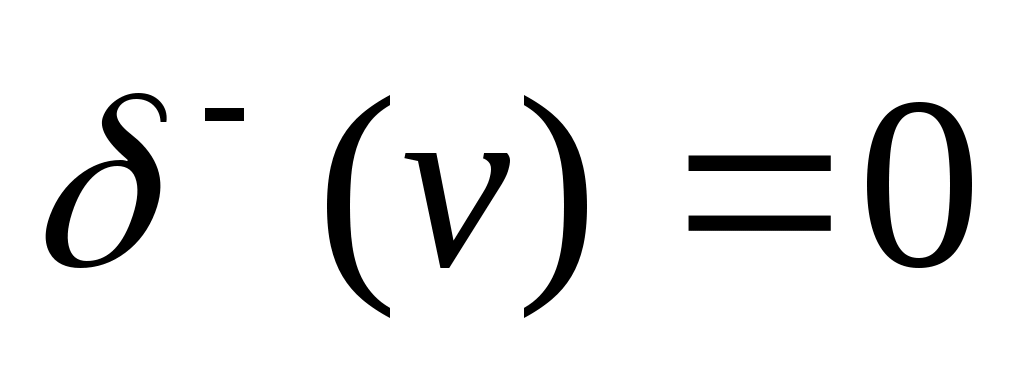 , то вершина v называется источником. , то вершина v называется источником.
Для орграфа 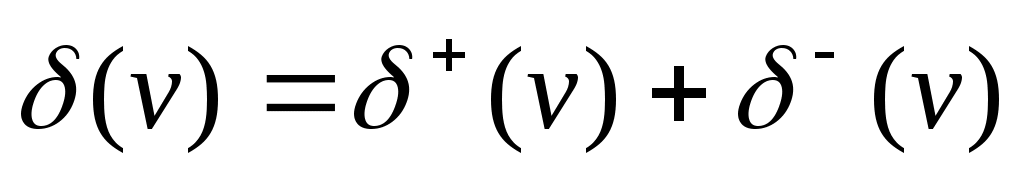 . Для нашего примера . Для нашего примера 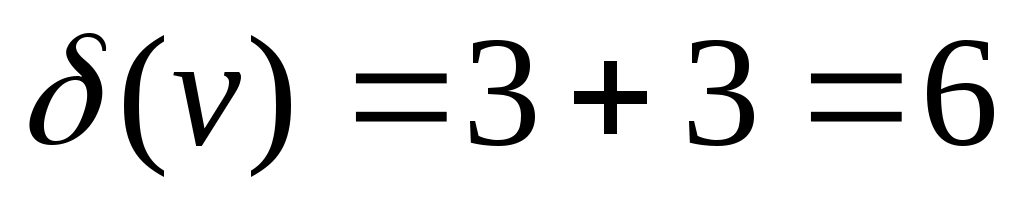 . .
Справедливы следующие теоремы.
Сумма степеней вершин неориентированного графа равна удвоенному числу ребер (лемма о рукопожатиях). Для орграфов эту теорему формулируют в другой форме: сумма полустепеней захода всех вершин орграфа D равна сумме их полустепеней исхода.
В графе число вершин нечетной степени четно.
Граф 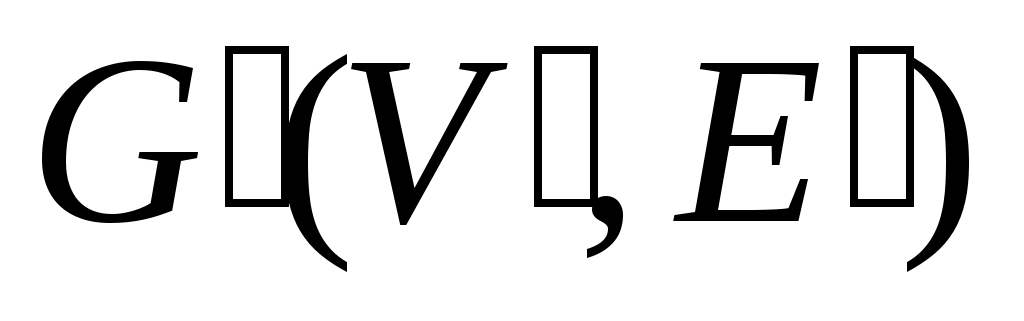 называется подграфом графа называется подграфом графа  , если , если 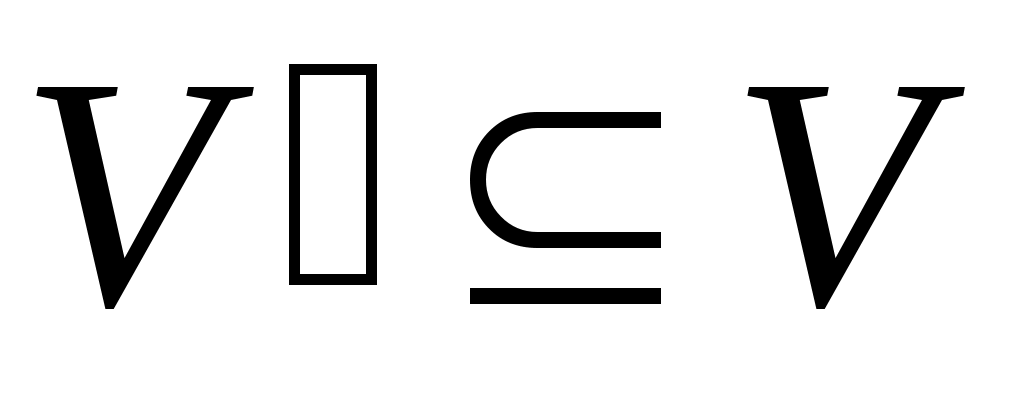 и и 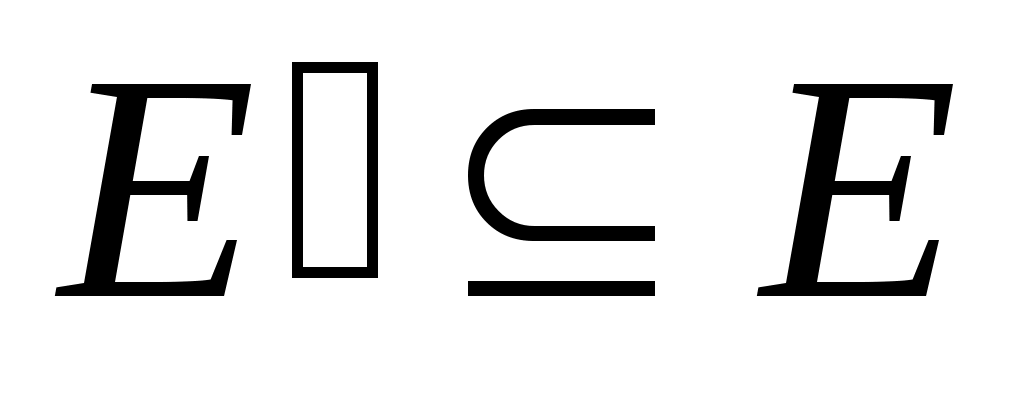 . Таким образом, каждая вершина в . Таким образом, каждая вершина в  является вершиной в является вершиной в 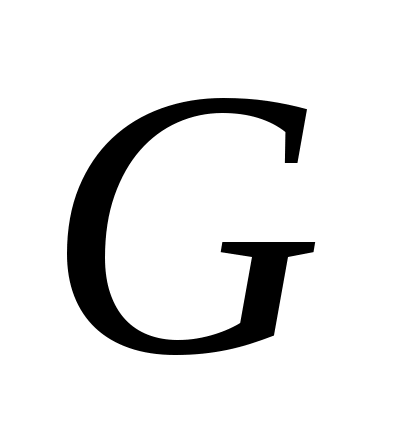 , и каждое ребро в , и каждое ребро в  является ребром в является ребром в 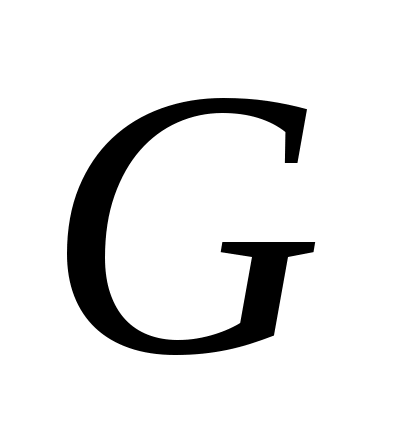 . Подграф называется собственным, если он отличен от самого графа. . Подграф называется собственным, если он отличен от самого графа.
На рис. 4 приведены граф 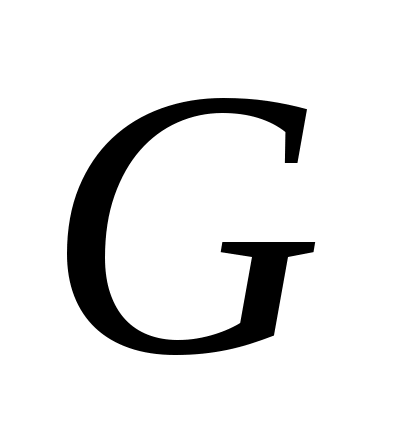 и его подграфы. и его подграфы.
 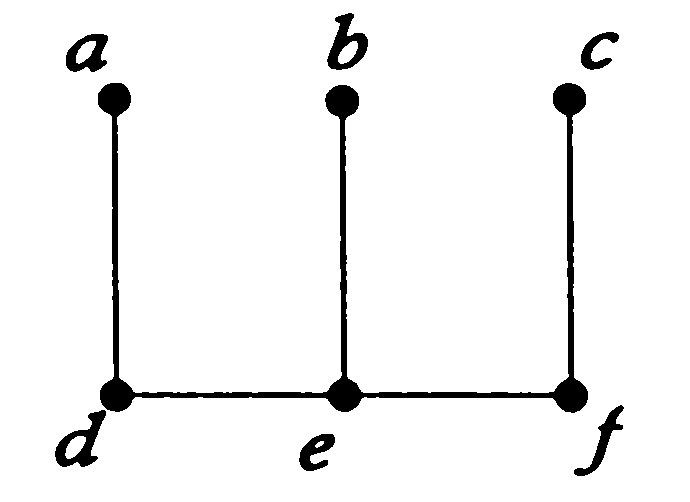 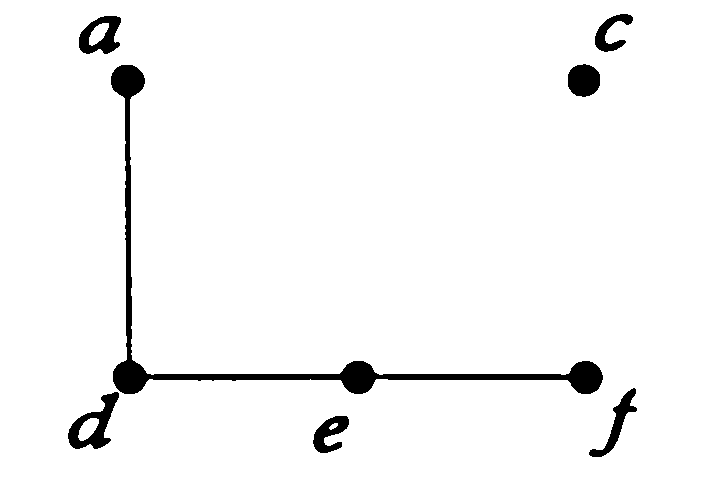
Рис. 4.
Два графа  и и 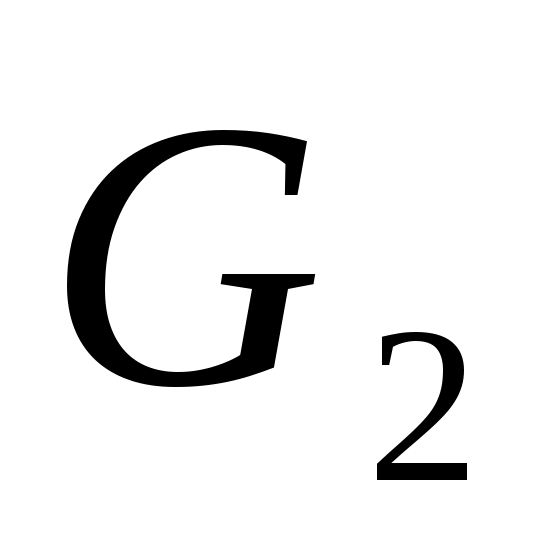 изоморфны, если существует такое взаимно-однозначное соответствие между множествами их вершин и ребер, что соответствующие ребра графов инцидентны соответствующим вершинам этих графов. Другими словами, если вершины изоморфны, если существует такое взаимно-однозначное соответствие между множествами их вершин и ребер, что соответствующие ребра графов инцидентны соответствующим вершинам этих графов. Другими словами, если вершины 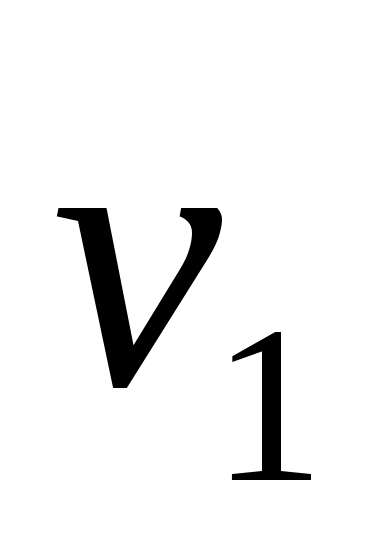 и и 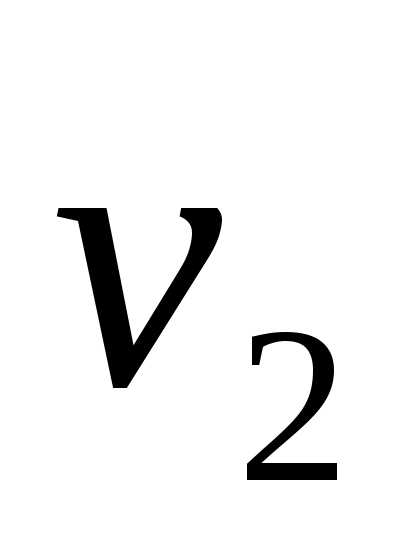 в в  соответствуют вершинам соответствуют вершинам 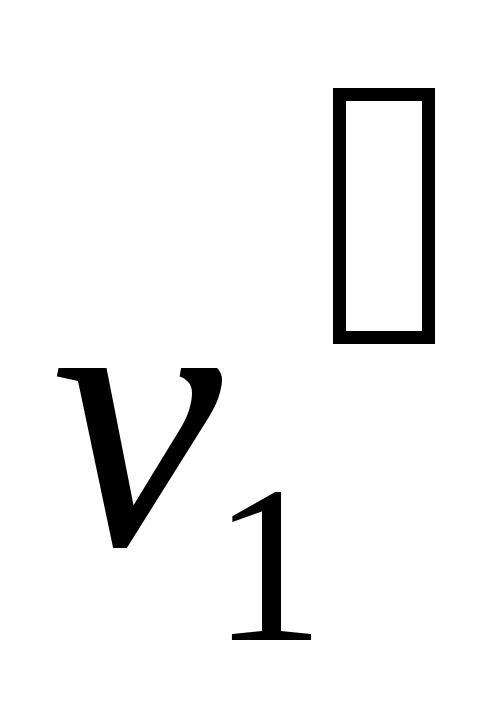 и и 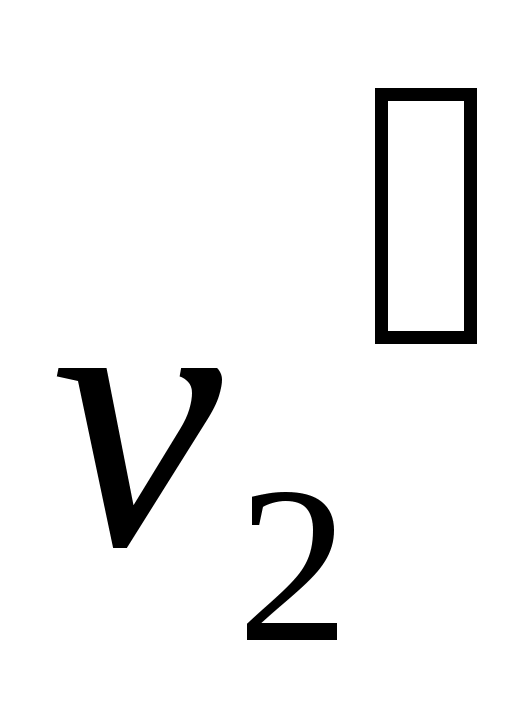 в в 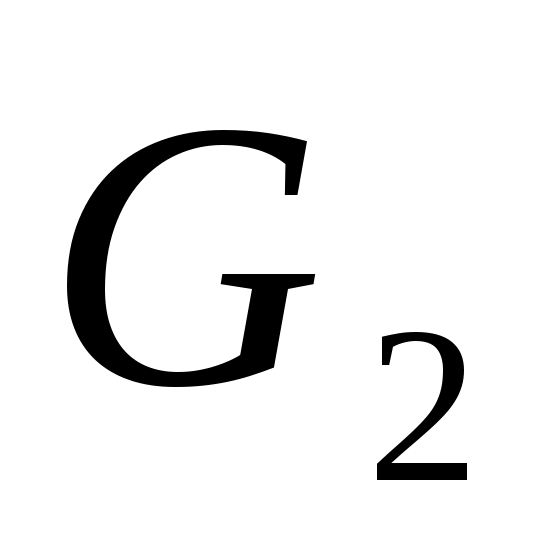 , то ребро в , то ребро в  , имеющие концевые вершины , имеющие концевые вершины 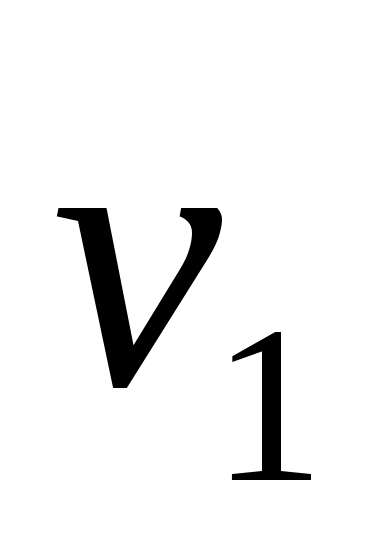 и и 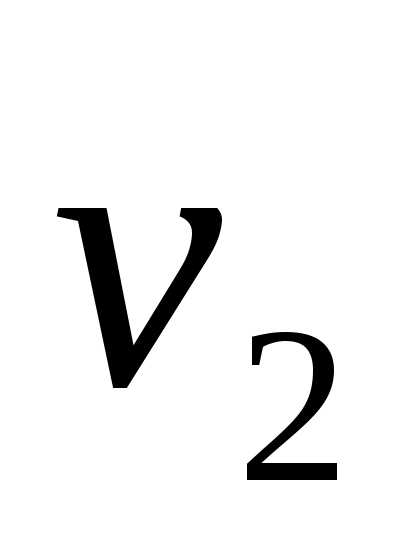 должно соответствовать ребру в должно соответствовать ребру в 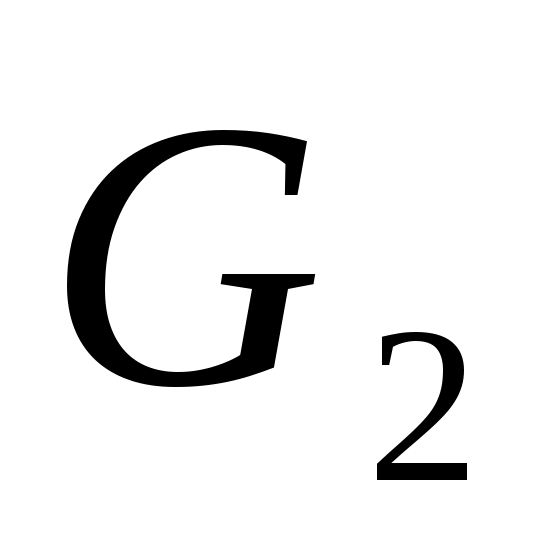 , имеющие концевые вершины , имеющие концевые вершины 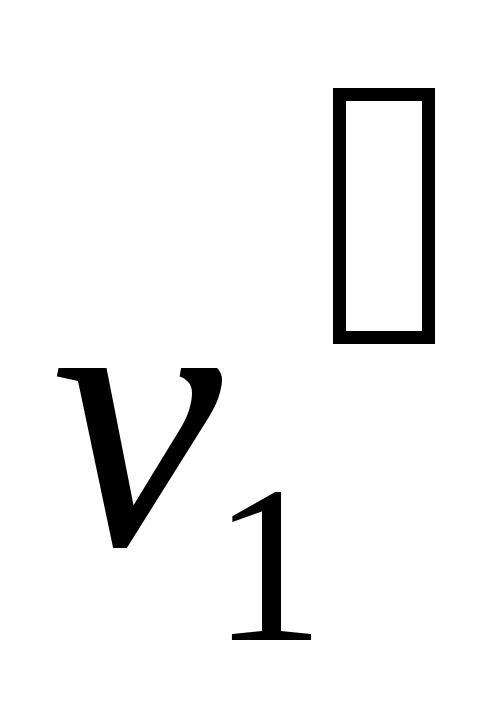 и и 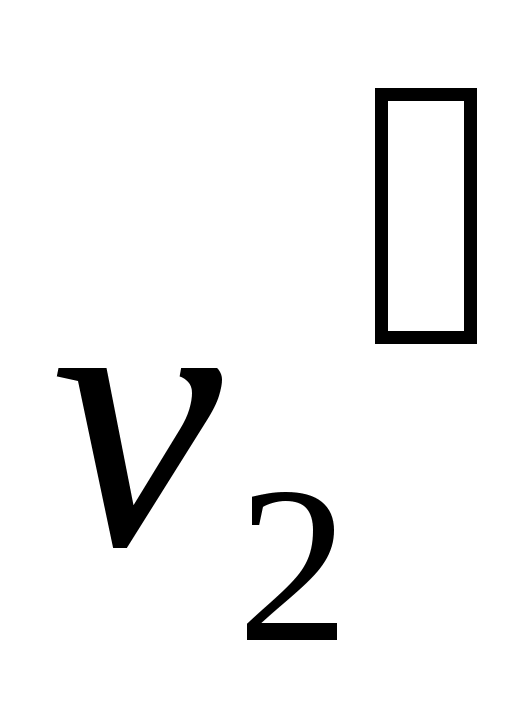 , и наоборот. На рис. 3 изображены изоморфные графы. , и наоборот. На рис. 3 изображены изоморфные графы.

Рис. 5.
Пусть  - неориентированный граф с вершинами - неориентированный граф с вершинами 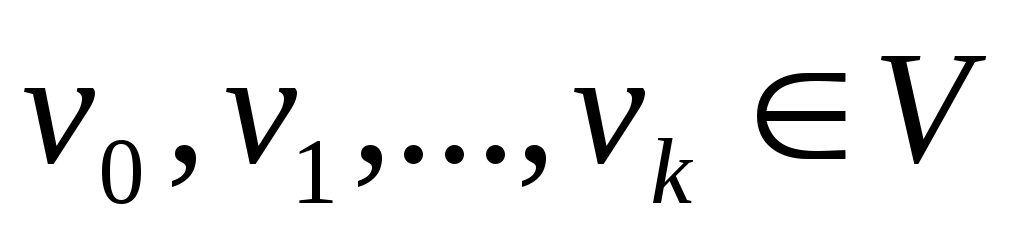 и ребрами и ребрами  . Маршруто длины kиз . Маршруто длины kиз 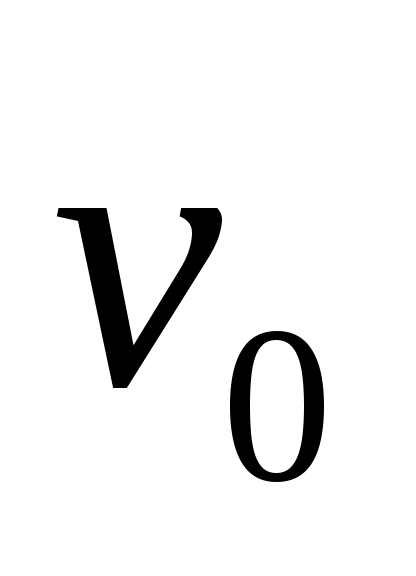 в в  называется последовательность называется последовательность 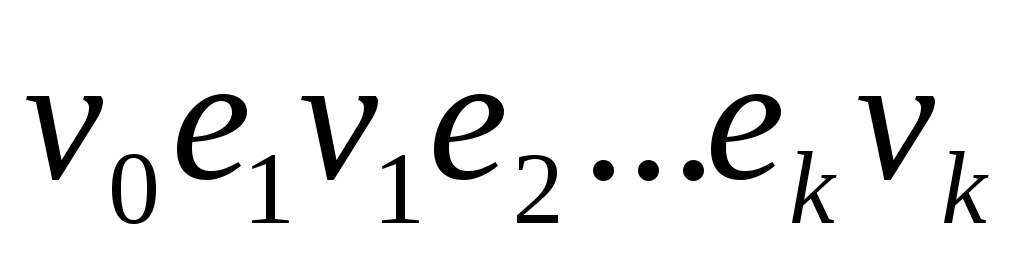 , такая что , такая что 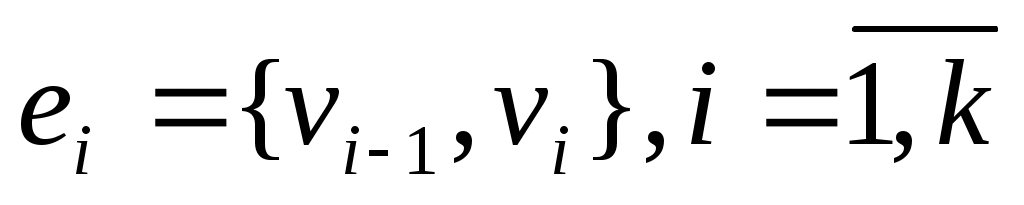 . В общем случае будем обозначать маршрут . В общем случае будем обозначать маршрут 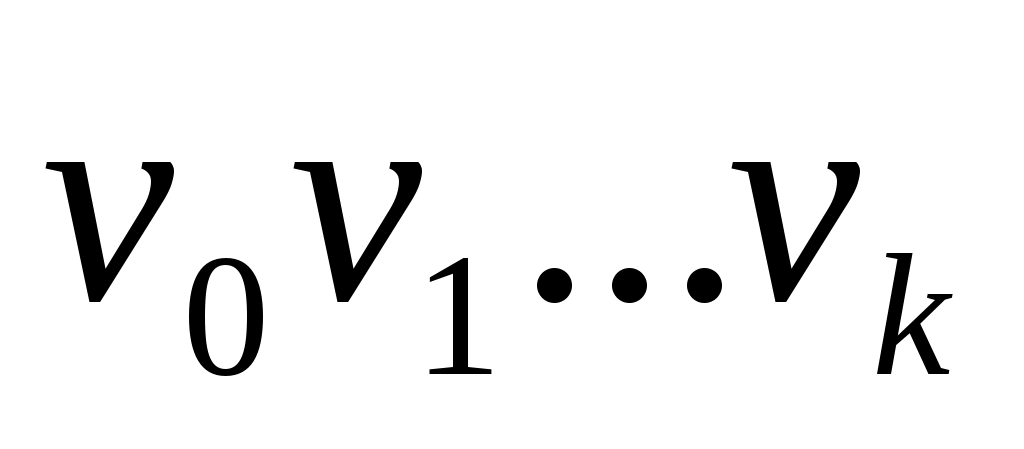 . Для орграфа будем говорить путь. Простым маршрутом называется маршрут, в котором нет повторяющихся вершин. Таким образом, маршрут – это совокупность ребер, которые объединены вместе с вершинами так, что вдоль них можно двигаться по графу, а длина пути – число этих ребер. . Для орграфа будем говорить путь. Простым маршрутом называется маршрут, в котором нет повторяющихся вершин. Таким образом, маршрут – это совокупность ребер, которые объединены вместе с вершинами так, что вдоль них можно двигаться по графу, а длина пути – число этих ребер.
Граф 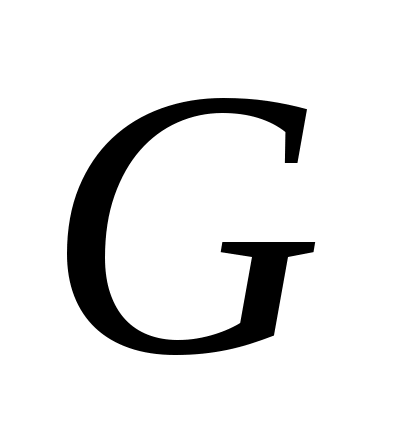 называется связным, если имеется маршрут (простой) между любыми двумя его различным вершинами. Все рассмотренные нами ранее графы являются связными. Отношение связанности является отношением эквивалентности. Изолированная вершины является компонентой связности. называется связным, если имеется маршрут (простой) между любыми двумя его различным вершинами. Все рассмотренные нами ранее графы являются связными. Отношение связанности является отношением эквивалентности. Изолированная вершины является компонентой связности.
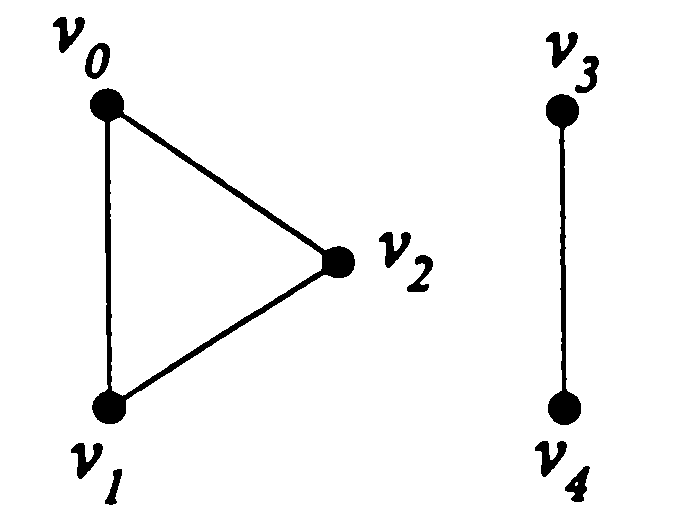
Рис. 6.
Граф, приведенный на рис. 6, не связанный.
Пусть задан граф  . Подграф . Подграф  графа графа 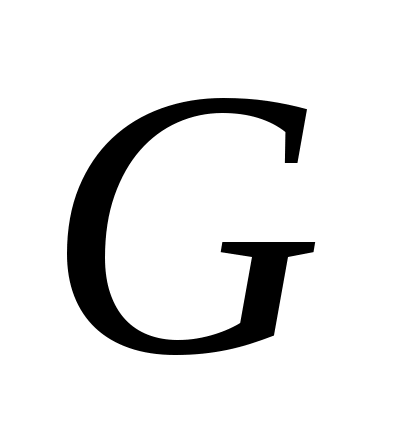 называется компонентой графа называется компонентой графа 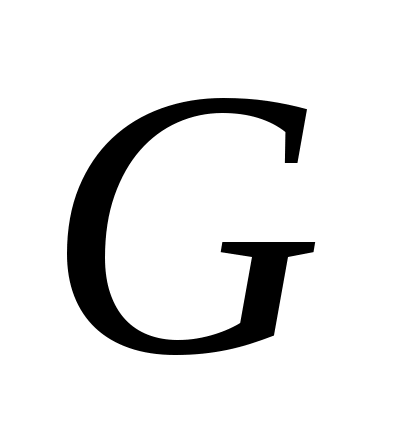 , если выполнены следующие два условия: , если выполнены следующие два условия:
 - непустой связный граф. - непустой связный граф.
 - максимальный связный подграф графа - максимальный связный подграф графа 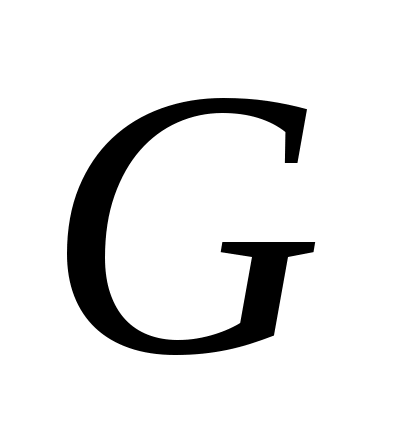 (т.е. компонента графа (т.е. компонента графа 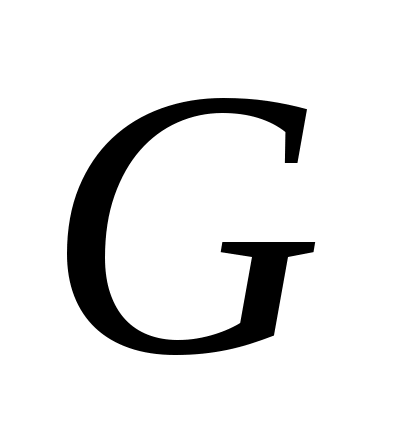 не является собственным подграфом любого другого связанного подграфа графа не является собственным подграфом любого другого связанного подграфа графа  ). ).
Если граф  связен, то он имеет только одну компоненту – граф связен, то он имеет только одну компоненту – граф  . .
Наш граф на рис. 6 имеет 2 компоненты. По определению изолированная вершина графа является его компонентой.
Как мы уже говорили, граф может задаваться графически. Для задания графа используются также матрицы смежности и инцидентности, которые однозначно определяют задаваемый граф.
Пусть задан граф  . Количество вершин графа, . Количество вершин графа, 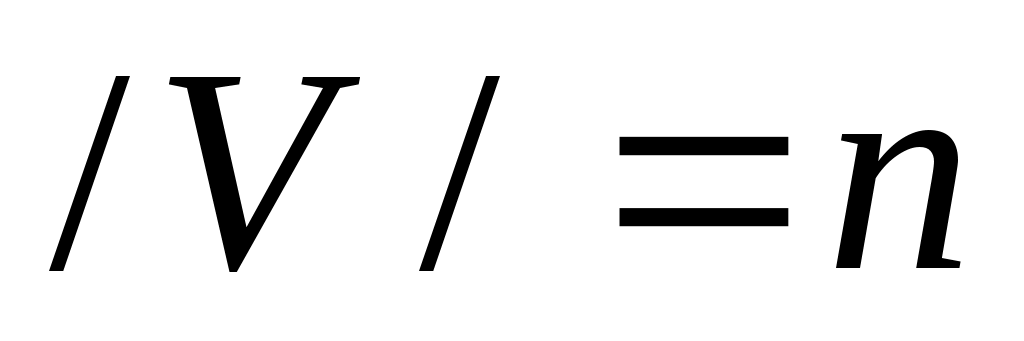 . Количество ребер графа, . Количество ребер графа, 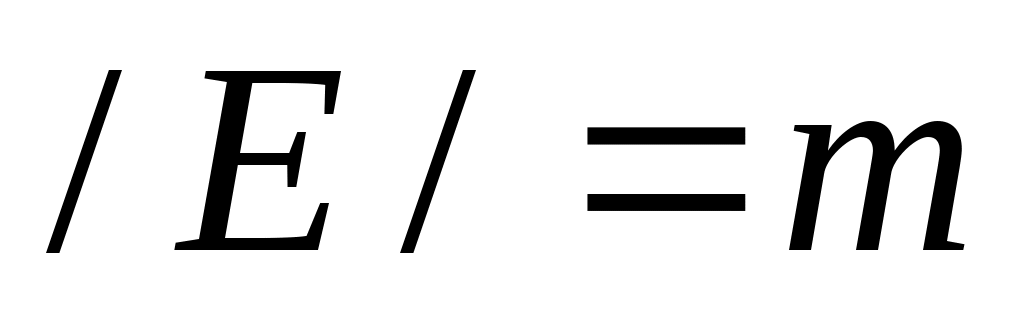 . Будем считать, что вершины и ребра (дуги) графа каким либо образом пронумерованы. . Будем считать, что вершины и ребра (дуги) графа каким либо образом пронумерованы.
Матрицей смежности A простогографа 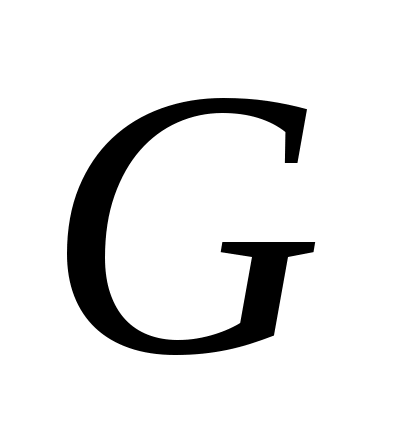 называется квадратная матрица размером называется квадратная матрица размером  , строкам и столбцам которой соответствуют вершины графа, записанные в том же самом порядке, а элемент i-ой строки и j-го столбца равен 1, если имеется ребро (дуга) из i-ой вершины в j-ую вершину, и равен нулю в противном случае. , строкам и столбцам которой соответствуют вершины графа, записанные в том же самом порядке, а элемент i-ой строки и j-го столбца равен 1, если имеется ребро (дуга) из i-ой вершины в j-ую вершину, и равен нулю в противном случае.
Матрица смежности является симметрической матрицей. Для простого графа сумма элементов строки (столбца) равна степени соответствующей вершины.
В случае мультиграфа соответствующий элемент  равен кратности ребра (дуги). При наличии в графе петель, элемент равен кратности ребра (дуги). При наличии в графе петель, элемент  равен числу петель, инцидентных данной вершине. Построим матрицы смежности для неориентированного графа (рис. 7.а, 8.а) и орграфа (рис. 7.б, 8.б). равен числу петель, инцидентных данной вершине. Построим матрицы смежности для неориентированного графа (рис. 7.а, 8.а) и орграфа (рис. 7.б, 8.б).
 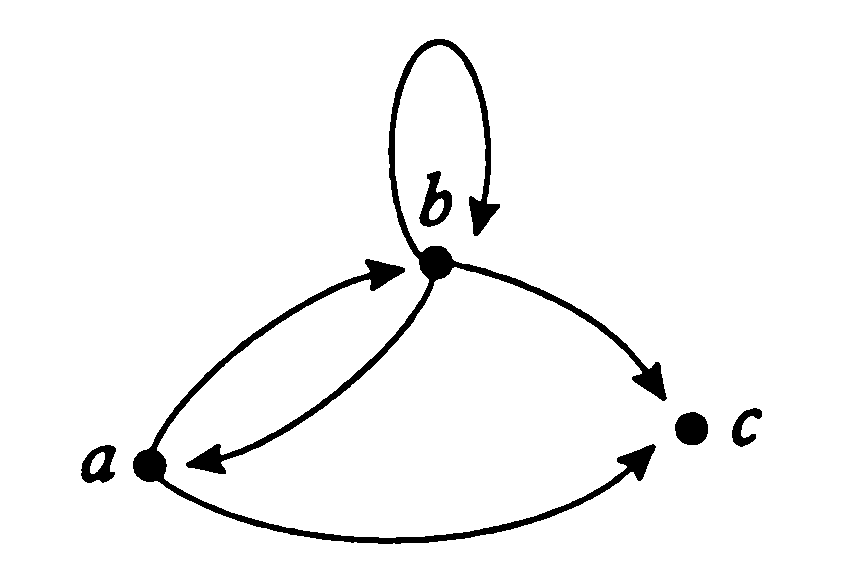
а. б.
Рис. 7.
 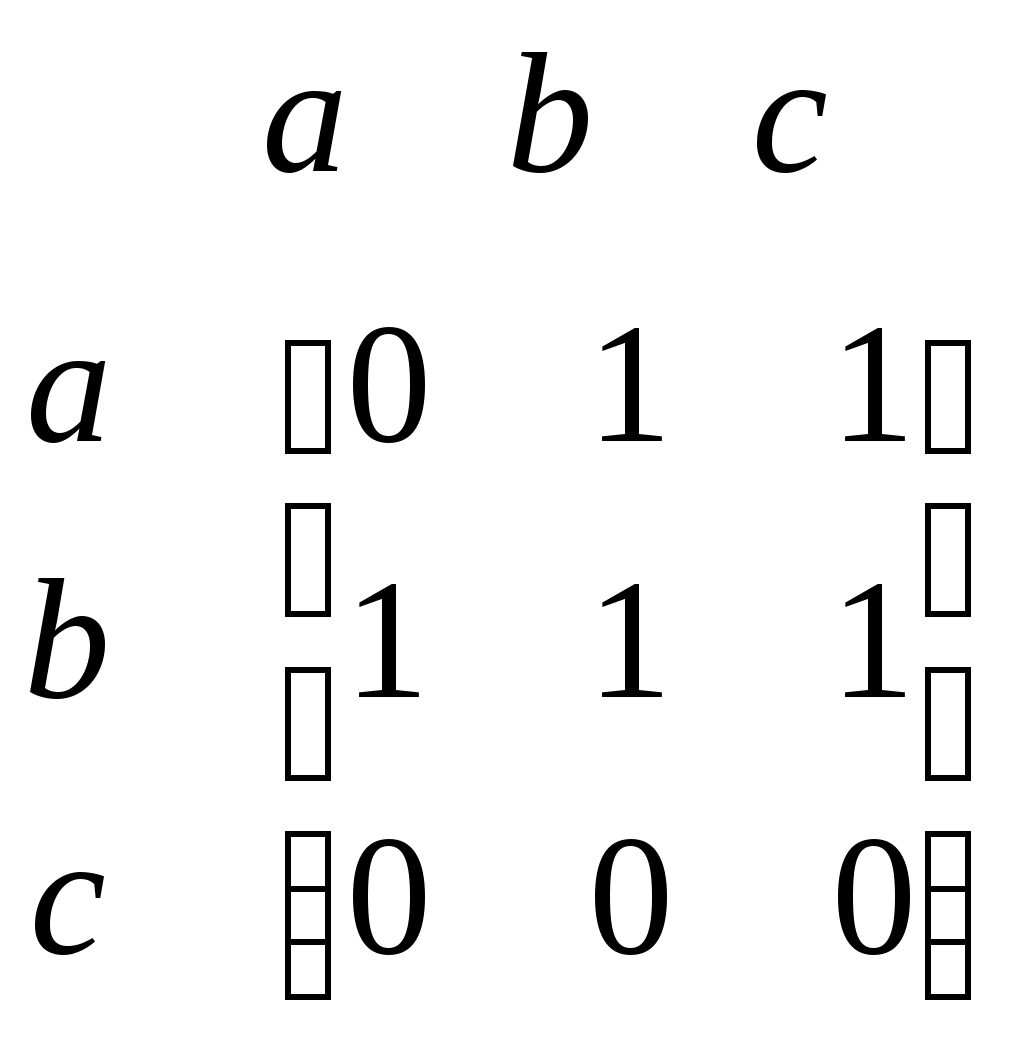
а. б.
Рис. 8.
Матрицей инцидентности B неориентированного графа  называется матрица размером называется матрица размером  , строкам матрицы которой соответствуют вершины графа, а столбцам – ребра графа , элемент i-ой строки и j-го столбца равен 1, если i-ая вершина инцидента j-ому ребру, и равен нулю в противном случае. , строкам матрицы которой соответствуют вершины графа, а столбцам – ребра графа , элемент i-ой строки и j-го столбца равен 1, если i-ая вершина инцидента j-ому ребру, и равен нулю в противном случае.
В матрице инцидентности для простого неориентированного графа сумма элементов строки также равна степени соответствующей вершины, а сумма элементов любого столбца равна 2. В случае наличия у графа петель сумма элементов соответствующего столбца равна единице.
Матрицей инцидентности B орграфа D называется матрица размером  , элементы которой опеделяются следующим образом: , элементы которой опеделяются следующим образом:

При наличии петли в орграфе соответствующий элемент 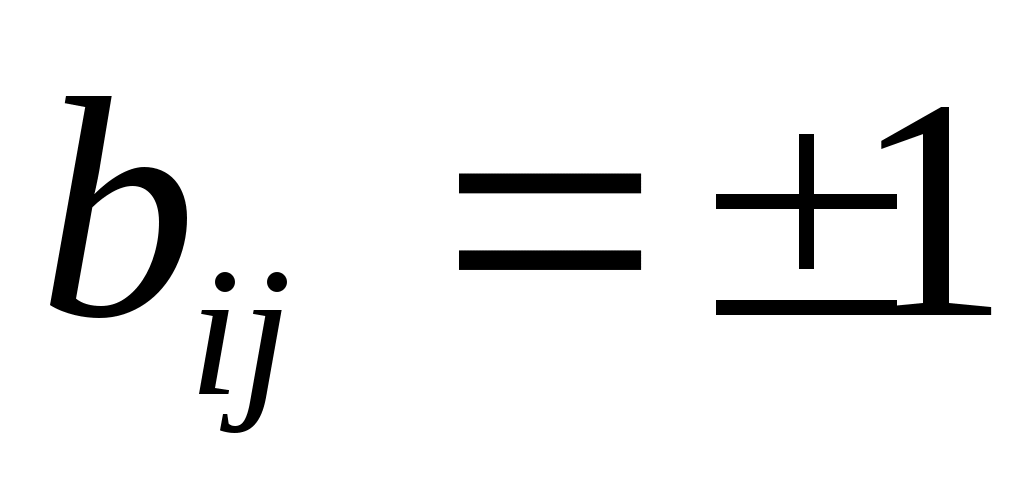 . .
Построим матрицы инцидентности для неориентированного графа и орграфа.
 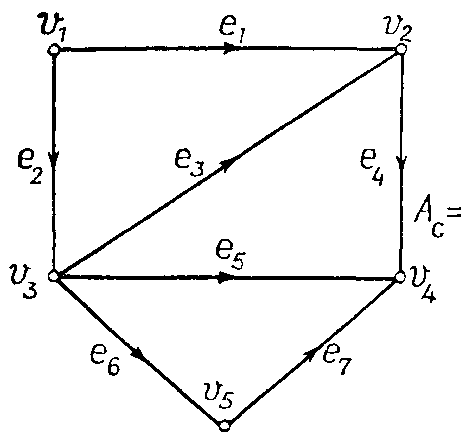
а. б.
Рис. 9.
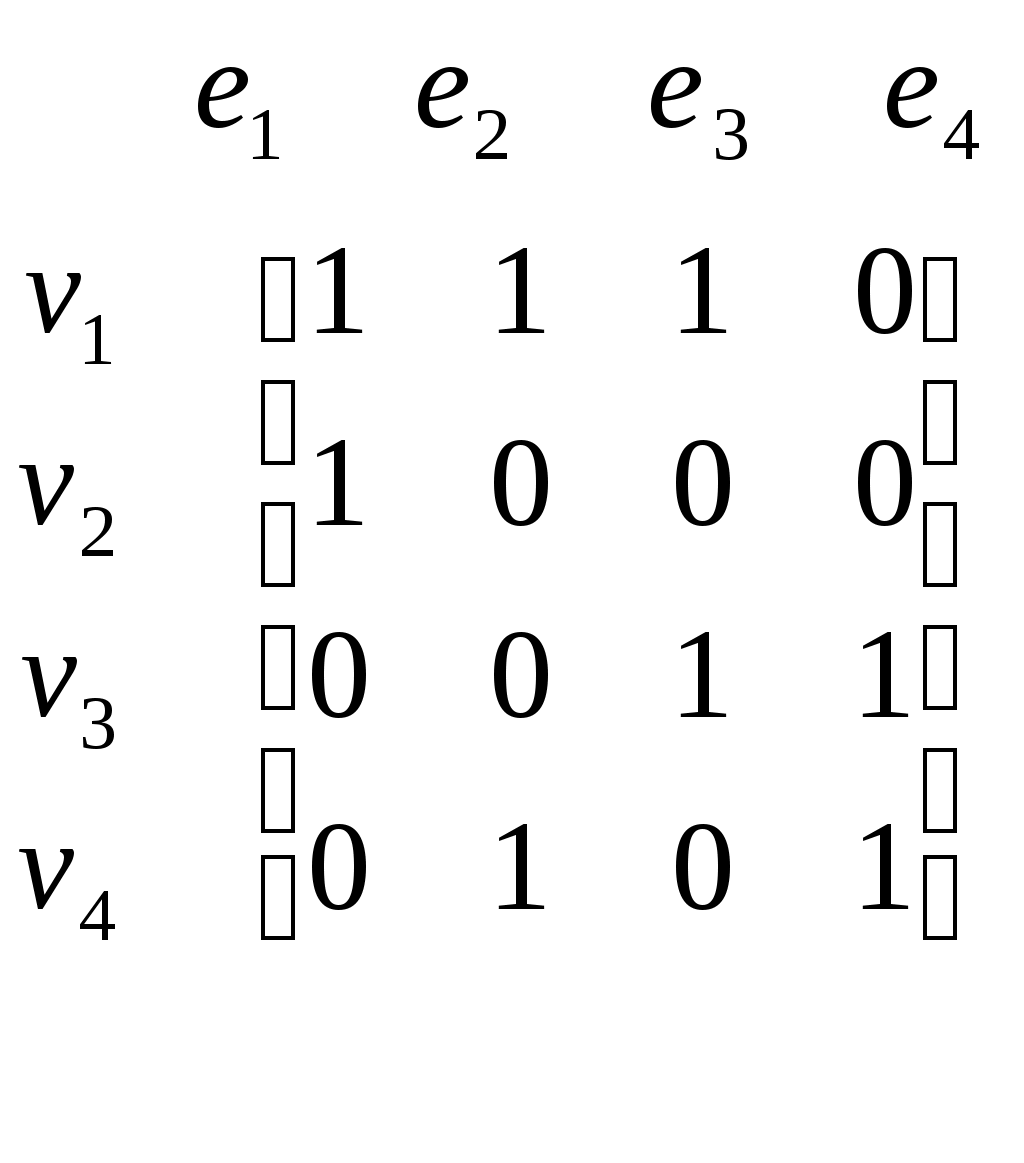 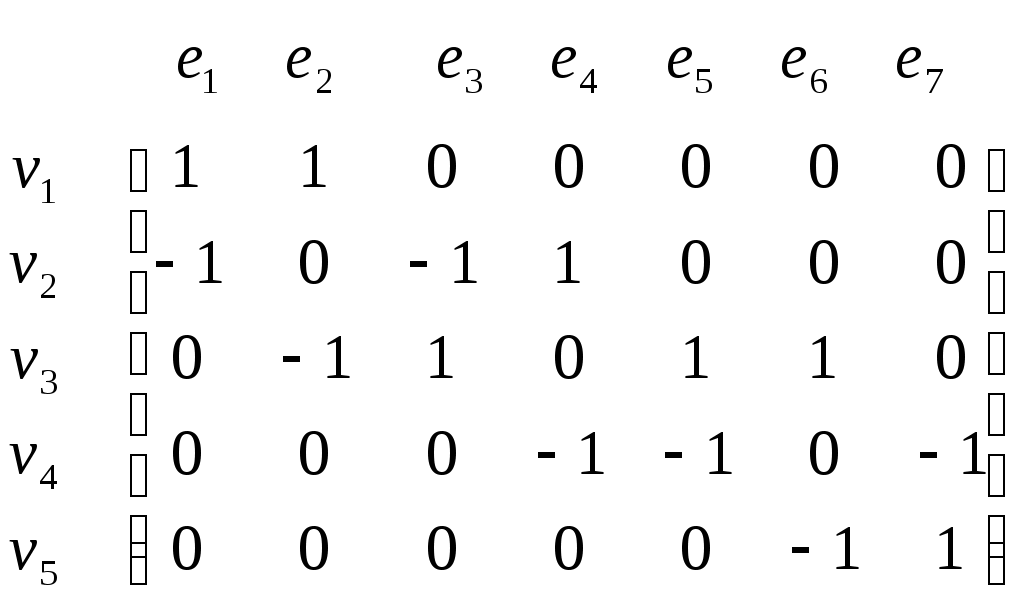
а. б
.
Рис. 10.
|
 Скачать 306 Kb.
Скачать 306 Kb.