КГУ «Алчановская ОСШ»
(Наименование организации образования)
Краткосрочный план по алгебре № 30.
Раздел
|
|
Учитель
|
Рыбинок Е.В.
|
Дата: «_______»
|
22.11.2022
|
Класс « 7 »
|
Количество присутствующих:
|
Количество отсутствующих:
|
Тема урока
|
Взаимное расположение графиков линейной функции.
|
Цели обучения в соответствии с учебной программой
|
7.4.1.8 обосновывать взаимное расположение графиков линейных функций в зависимости от значений их коэффициентов
|
Цели урока
|
Отрабатывать навыки построения графиков функции вида y=kx+b;
выяснение влияния значений k и b на положение графиков;
выяснение влияния значения параметра k на взаимное расположение графиков линейных функций.
|
Ход урока
|
Этап урока/время
|
Действия педагога
|
Действия ученика
|
Оценивание
|
Ресурсы
|
Начало урока
3 мин
|
Организационный момент. Приветствует учеников,проверяет готовность к уроку (учебник, тетрадь, дневник, ручка, карандаш), жела-ет успеха.
Психологический настрой на деятельность.
Провести игру «Комплементы»
Деление на группы.
Учащиеся делятся на группы с помощью геометрических фигур «Квадрат» и «Треугольник».
|
Приветствуют учителя и друг друга
Стоя в кругу, учащиесяберутсязаруки. Глядя в глазасоседу, говорятемунесколькодобрыхслов. Принимающийкиваетголовой и говорит: «Спасибо, мнеоченьприятно!»Затемондариткомплиментсвоемусоседу.
Учащиеся объединя-ются в группы
|
|
Фигуры
|
Повторение
7 мин
|
1. Проверка домашнего задания.
2. По методу «Толстые и тонкие вопросы»
- Какую функцию называют линейной?
- Что является графиком линейной функции?
- Сколько нужно отметить точек на координатной плоскости, чтобы построить прямую?
- Как построить график линейной функции?
- Какую функцию называют прямой пропорциональностью?
- Что является графиком прямой пропорциональности?
- Как его построить?
- В каких координатных четвертях расположен график функции у = kх + b при k<0, k>0?
- Как называется k?
3. Устная работа.
А) Назовите угловой коэффициент линейной функции?
у = 9х + 10 у = 7х – 2 у = –3х + 5
у = х – 11 у = 0,9х – 2 у = 1,3х + 5
Б) Функция задана формулой у = f(x) = 2х – 4
Найдите: f(–2);f(0); f(–1); f(3).
|
Учащиеся обсуждают с учителем выполненное домашнее задание.
Выполняют коллективно задания. Повторяют пройденный материал.
|
За прави-льный от-вет полу-чают же-тон
|
Жетоны
Слайд 2
|
Середи-
на урока
28 мин
|
Подготовка к восприятию новой темы. Определить цели урока.
- Как могут располагаться две произвольные прямые на плоскости?
( Две прямые могут быть параллельными, могут пересекаться и совпадать)
Исходя, из проделанной работы определите тему урока и цели урока.
А теперь выясним, что нового должны узнать на уроке, что выяснить, чему научиться? (Расположение графиков линейных функций)
На основе предыдущих рассуждений попытайтесь самостоятельно сформули-ровать тему урока. ( Взаимное расположение графиков линейных функций)
Изучение нового материала.
Мы с вами знаем, что графиком линейной функции является прямая, поэтому графики двух линейных функций тоже могут быть параллельными, могут пересекаться и совпадать.
Проблемный вопрос:
- От чего зависит параллельность, пересечение, совпадение графиков линейных функций?
А сейчас вы выполните графическую работу, которая поможет вам ответить на поставленные вопросы.
Работа в группах.
Первая группа.
Задание:
В одной системе координат постройте графики функций:
у = 0,5x+1,5; y= 0,5x; y=0,5x-2.
Вторая группа.
Задание:
В одной системе координат постройте графики функций:
y=-x+3; y=1,5x+3; y=0,25x+3
- Построение графика функции под цифрой 3 выполняется, если уже построено по два графика в каждой группе заданий.
-В итоге выполнения заданий у вас в тетради должны быть изображены две системы координат, в каждой из которых обязательно по два графика. У сильных учащихся в тетрадях возможно - по три графика.
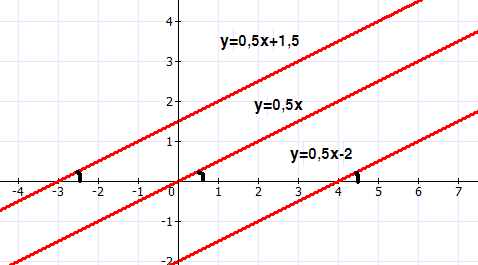
- Что можно сказать про графики линейных функций? (они параллельны)
- Что можно сказать про коэффициенты b и k в формулах? (k равны, b не равны)
Вывод: (если у линейных функций угловой коэффициент одинаковый, то их графики параллельны)
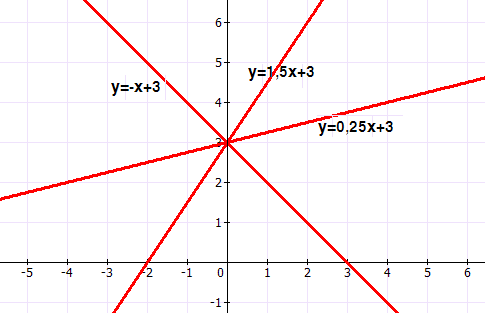
- Что можно сказать про графики линейных функций? (они пересекаются в одной точке (0;3))
- Что можно сказать про коэффициенты b и k в формулах? (b равны, k не равны)
Вывод: (график линейной функции пересекает ось OY в точке (0;b))
Обратите внимание на цели, которые вы поставили в начале урока. На какой вопрос осталось ответить? (в каком случае графики двух функций совпадают)
-В каком же случае графики двух функций совпадают? (графики двух функций совпадают, если совпадают k и b.
Работа устная по чертежам. Вывод записать в тетрадь.
1. k > 0 => Угол наклона прямой к оси Ох острый;
k < 0 => Угол наклона прямой к оси Ох тупой;
k = 0 => прямая параллельна оси Ох;
2. b => график пересекает ось Оу выше оси Ох;
b => график пересекает ось Оу ниже оси Ох;
b => график проходит через начало координат (прямая пропорциональность).
3. Даны функции заданные формулами: у = k1х + b1 и у = k2х + b2
k1 = k2, b1 = b2 => графики функций совпадают,
k1 = k2, b1 ≠ b2 => графики функций параллельны,
k1 ≠ k2 => графики пересекаются,
k1 ≠ k2, b1 = b2 => графики пересекаются в точке (0,b).
Работа в парах.
1. Определить по графику знак углового коэффициента k и число b
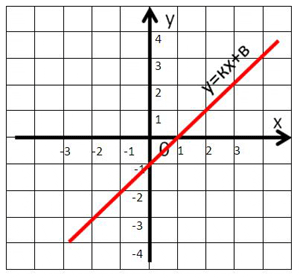
k > 0,b = -1
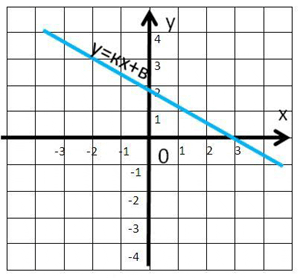
k < 0,b = 2
2. Среди функций, заданных формулами:
1) у = х + 0,5;
2) у = 1 + 0,5х;
3) у = 2х –5;
4) у = -0,5х + 4;
5) у = 5х = 1;
6) у = 0,5х –2
назовите те, которые:
а) параллельны графику функции
у = 0,5х + 4
б) пересекаются с графиком функции
у = 2х + 3
в) совпадают с графиком функции
у = 4 – 0,5х
|
Учащиеся определяю тему и цели урока
Учащиеся выполняют работу в группах. Отвечают на вопросы и делают выводы. Проверить правильность построения графиков по слайдам.
Учащиеся отвечают на вопросы и делают выводы.
Выполняют работы.
Обмениваются друг с другом тетрадями по часовой стрелке и проверяют.
|
Устный комментарий учителя
Устный комментарий учителя
Устный комментарий учителя.
Апладис-менты
Устный комментарий учи-теля. За каждое правиль-ноереше-ние зада-ния полу-чают по жетону
|
Слайд 3
Слайд 4
Слайд 5
Слайд 6
Слайд 7
Слайд 8
|
Конец урока
2 мин
|
Рефлексия.
«Две звезды и одно пожелание».
Домашнее задание.
Выучить выводы. Выполнить по учебнику №
|
Подводят итоги.
Записывают домашнее задание.
|
Устный комментарий учи-теля.
Устный комментарий учи-теля.
|
Учебник
Слайд 9
| |
 Скачать 91.07 Kb.
Скачать 91.07 Kb.



