Исследование функций Тема Теоремы дифференцирования и применение производных Общее количество вопросов 20 (из 60)

• Название: Исследование функций Тема Теоремы дифференцирования и применение производных Общее количество вопросов 20 (из 60)
• Дата: 04.06.2022
• Размер: 207.41 Kb.
• Имя файла: rubezhny_kontrol_2_modulya_2.docx
• Тип: Исследование; #568581

Рубежный контроль 2 модуля 2

Раздел 4. «Дифференциальное исчисление»

Тема 4.1. Производная функции.

Тема 4.2. Дифференциал функции.

Тема 4.3. Производные высших порядков

Тема 4.4. Исследование функций

Тема 4.5. Теоремы дифференцирования и применение производных
Общее количество вопросов – 20 (из 60).

Время прохождения теста – 120 минут.

Максимальное количество баллов за тест – 100.

Заголовки секций НЕ показывать.

№ секции	Кол-во вопросов	выборка
1. Тема 4.1. Теория	14	6
2. Тема 4.1. Вычисление производных.	10	4
3. Темы 4.2, 4.3.	8	4
4. Тема 4.4.	18	4
5. тема 4.5.	10	2
Итого	60	20

Критерии оценивания

Количество баллов	<65	65>
Зачет	не зачтено	Зачтено

Секция 1. Тема 4.1. Производная функции. Теория.
(??) Величины х и у называются, соответственно

(!) приращение аргумента и функции

(?) приращение функции и аргумента

(?) аргумент и функция

(?) функция и аргумент

(??) Как называется операция нахождения производной?

(!) дифференцирование

(?) логарифмирование

(?) потенцирование

(?) абстрагирование

(??) Геометрический смысл производной в точке x₀:

(!) тангенс угла наклона касательной в точке x₀

(?) угол наклона секущей в точке x₀

(?) угол наклона касательной в точке x₀

(?) тангенс угла наклона секущей в точке x₀

(??) Производной функции является следующий предел: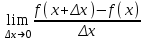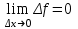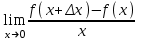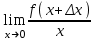

(!)

(?)

(?)

(?)

(??) Производная функции определяет:

(!) скорость изменение функции при изменении аргумента

(?) изменение аргумента при заданном изменении функции

(?) скорость изменения приращения функции при изменении аргумента

(?) изменение аргумента при заданном значении функции

(??) Угловой коэффициент касательной, проведенной к графику функции в некоторой точке, равен

(!) значению производной функции в этой точке

(?) отношению значения функции к значению аргумента в этой точке

(?) значению функции в этой точке

(?) значению тангенса производной функции в этой точке

(??)Производная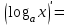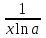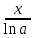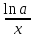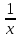



(!)

(?)

(?)

(?)

(??) Производная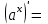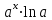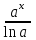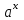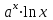



(!)

(?)

(?)

(?)

(??) Производная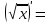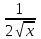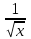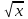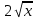



(!)

(?)

(?)

(?)

(??) Производная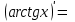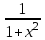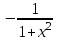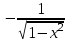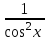



(!)

(?)

(?)

(?)

(??) Производная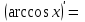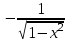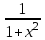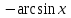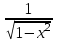



(!)

(?)

(?)

(?)

(??) Укажите функции, для которых существует конечная производная в каждой точке числовой оси: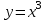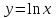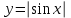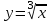

(!)

(?)

(?)

(?)

(??) Производная разности двух функций u и v равна:

(!) (u-v) = u - v

(?)(u-v) = u + v

(?)(u-v) = u / v

(?)(u-v) = uv + u v

(??) Производная произведения двух функции u и v равна:

(!) (u∙v) = uv + u v

(?)(u∙v) = u + v

(?)(u∙v) = u / v

(?)(u∙v) = u - v

Секция 2. Тема 4.1. Вычисление производных.
(??)Найдите производную следующей функции: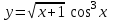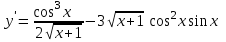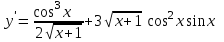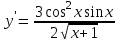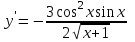



(!)

(?)

(?)

(?)

(??)Найдите производную следующей функции: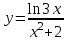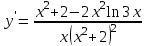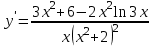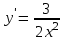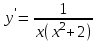



(!)

(?)

(?)

(?)

(??)Найдите производную следующей функции: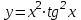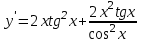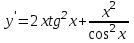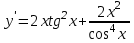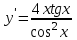



(!)

(?)

(?)

(?)

(??)Найдите производную следующей функции: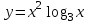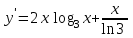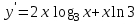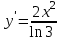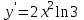



(!)

(?)

(?)

(?)

(??)Найдите производную следующей функции: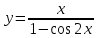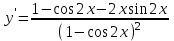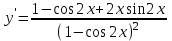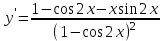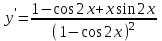



(!)

(?)

(?)

(?)

(??)Найдите производную следующей функции: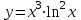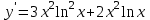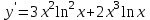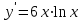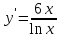



(!)

(?)

(?)

(?)

(??)Найдите производную следующей функции: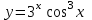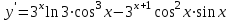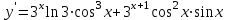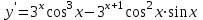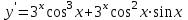



(!)

(?)

(?)

(?)

(??)Найдите производную следующей функции: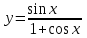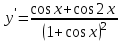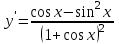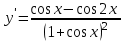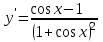



(!)

(?)

(?)

(?)

(??) Составьте уравнение касательной к графику функции: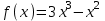



в точке x₀=1.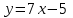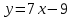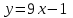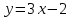

(!)

(?)

(?)

(?)

(??) Составьте уравнение касательной к графику функции: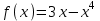



в точке x₀=1.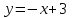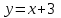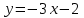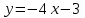

(!)

(?)

(?)

(?)

Секция 3. Тема 4.2- 4.3. Дифференциал функции. Производные высших порядков
(??) Дифференциал функции – это:

(!) главная линейная часть приращения функции при заданном изменении аргумента

(?) полное приращение функции при заданном изменении аргумента

(?) квадрат приращения функции при заданном изменении аргумента

(?) изменение функции при заданном изменении аргумента

(??) Дифференциал постоянной равен...

(!) нулю

(?) этой постоянной

(?) бесконечно большой величине

(?) невозможно определить

(??) Какое из следующих утверждений верно для нелинейной функции?

(!) дифференциал функции равен части приращения функции

(?) дифференциал функции равен производной этой функции

(?) дифференциал функции равен приращению аргумента

(?) дифференциал функции - это постоянная величина

(??) Производная производной функции называется

(!) второй производной

(?) первой производной

(?) производной первого порядка

(?) производной нулевого порядка

(??) Дифференциал суммы двух функций u и v равен: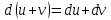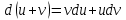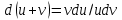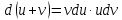

(!)

(?)

(?)

(?)

(??) Дифференциал отношения двух функций u и v равен: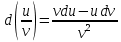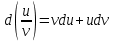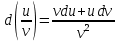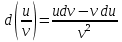

(!)

(?)

(?)

(?)

(??) Найти производные второго порядка функции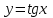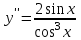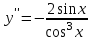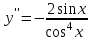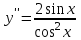



(!)

(?)

(?)

(?)

(??) Найти производные второго порядка функции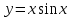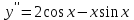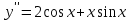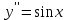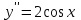



(!)

(?)

(?)

(?)
Секция 4. Тема 4.4. Исследование функций
(??) Функция называется монотонно возрастающей, если при х > 0:

(!) приращение функции y > 0

(?) приращение функции y = 0

(?) приращение функции y=1

(?) приращение функции y < 0

(??) Функция называется монотонно убывающей, если при х > 0:

(!) приращение функции y < 0

(?) приращение функции y = 0

(?) приращение функции y > 0

(?) приращение функции y =1

(??) Функция имеет в точке a максимум, если первая производная в этой точке:

(!) меняет знак с плюса на минус

(?) меняет знак с минуса на плюс

(?) остается постоянной

(?) стремится к бесконечности

(??) Функция имеет в точке a минимум, если первая производная в этой точке:

(!) меняет знак с минуса на плюс

(?) меняет знак с плюса на минус

(?) остается постоянной

(?) не меняет знак

(??) Функция выпукла вверх, если: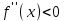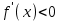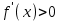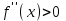

(!)

(?)

(?)

(?)

(??) Коэффициент k наклонной асимптоты y=kx+b определяется из условия: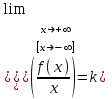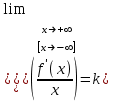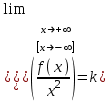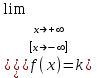

(!)

(?)

(?)

(?)

(??) Функция f(x) возрастает на некотором интервале, если на этом интервале: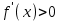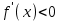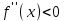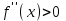

(!)

(?)

(?)

(?)

(??) Вертикальная асимптота находится в точке:

(!) разрыва 2 рода

(?) разрыва 1 рода

(?) в точке, где график функции имеет две наклонные

(?) устранимого разрыва

(??) Функция выпукла вниз, если: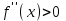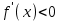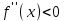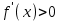

(!)

(?)

(?)

(?)

(??) Коэффициент b наклонной асимптоты y=kx+b определяется из условий: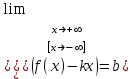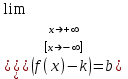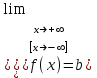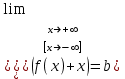

(!)

(?)

(?)

(?)

(??) В точке перегиба графика функции:

(!) график меняет направление выпуклости

(?) график проходит через максимум

(?) функция меняет знак

(?) меняется знак производной

(??) Для дифференцируемой функции f(x) из приведенных условий выберите необходимое условие точки перегиба: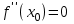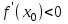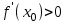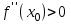

(!)

(?)

(?)

(?)

( ??) Функция y=x³+x

(!) всюду возрастает

(?) возрастает на (-∞,0)

(?) убывает на (0,+ ∞)

(?) всюду убывает

(??) Определите промежуток убывания функции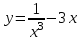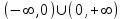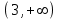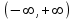



(!)

(?)

(?)

(?) нет промежутка убывания

(??) Определите количество точек перегиба функции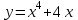



(!) ни одной

(?) одну

(?) две

(?) больше трех

(??) Функция убывает, если: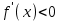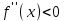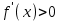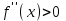

(!)

(?)

(?)

(?)

(??) Укажите точки экстремума непрерывной на всей числовой прямой функции y(x), если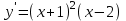



(!) х = 2 – точка min

(?) х = 2 – точка max

(?) х = -1 – точка max

(?)х = -1 – точка min

(??) Найдите асимптоты функции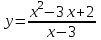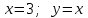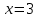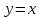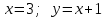



(!)

(?)

(?)

(?)

Секция 5. Тема 4.5. Теоремы дифференцирования и применение производных
(??) Рассмотрим следующую теорему:



Имя какого ученого носит эта теорема?

(!) Ферма

(?) Коши

(?) Лопиталь

(?) Бернулли

(??) Выберите верное утверждение:

(!) если функция дифференцируема в точке, то она непрерывна в этой точке. Обратное утверждение неверно

(?) если функция непрерывна в точке, то она дифференцируема в точке

(?) если функция дифференцируема в точке, то она непрерывна в этой точке. Обратное утверждение верно

(?) если функция непрерывна в точке, то она дифференцируема в точке. Обратное утверждение неверно

(??) Укажите верное утверждение: если функция дифференцируема в некоторой точке, то в этой точке ...

(!) можно провести касательную к графику функции

(?) функция не определена

(?) нельзя провести касательную к графику функции

(?) функция имеет экстремум

(??) Согласно теореме Ролля существует точка cиз интервала(a; b), в которой производная функции равна нулю, если

(!) функция непрерывна на отрезке [a; b], дифференцируема на интервале (a; b) и имеет на концах равные значения

(?) функция дифференцируема на интервале (a; b) и имеет на концах равные значения

(?) функция непрерывна на отрезке [a; b] и имеет на концах равные значения

(?) функция непрерывна на отрезке [a; b], дифференцируема на интервале (a; b)

(??) Согласно теореме Лагранжа, существует точка cиз интервала(a; b), в которой



если

(!) функция непрерывна на отрезке [a; b], дифференцируема на интервале (a; b)

(?) функция дифференцируема на интервале (a; b)

(?) функция непрерывна на отрезке [a; b]

(?) функция непрерывна на отрезке [a; b], дифференцируема на интервале (a; b) и имеет на концах равные значения

(??) Правило Лопиталя для вычисления пределов имеет следующий вид: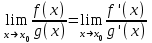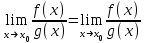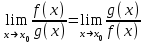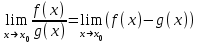

(!)

(?)

(?)

(?)

(??) Применяя правило Лопиталя, вычислите предел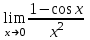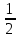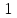



(!)

(?)

(?) 0

(?) ∞

(??) Применяя правило Лопиталя, вычислите предел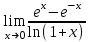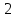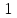



(!)

(?)

(?) 0

(?) ∞

(??) Производная функции y=y(x), заданной параметрически x=x(t), y=y(t), может быть найдена по формуле: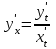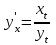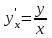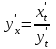

(!)

(?)

(?)

(?)

(??) Найти производную функции y(x), заданной параметрически: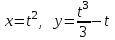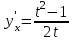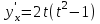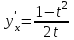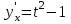



(!)

(?)

(?)

(?)

(??) Найти производную функции y(x), заданной параметрически: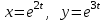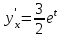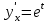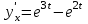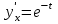



(!)

(?)

(?)

(?)