Урок. урок. Взаимное расположение прямых в пространстве. Угол между двумя прямыми. Учебная цель занятия
 Скачать 0.88 Mb. Скачать 0.88 Mb.
|
|
Взаимное расположение прямых в пространстве. Угол между двумя прямыми. Учебная цель занятия: научить учащихся решать задачи по теме. Задачи: обобщить и систематизировать теоретические сведения пройденной темы; отработать умения учащихся по решению задач пройденной темы; развивать пространственное мышление учащихся; активизировать внимание учащихся с помощью применения мультимедийных средств; прививать интерес к предмету. Перечень вопросов, рассматриваемых в теме признаки скрещивающихся прямых; определение углов с сонаправленными сторонами; доказательство теоремы о плоскости, проходящей через одну из скрещивающихся прямых; доказательство теоремы о равенстве углов с сонаправленными сторонами. Основная литература: Учебник Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. Геометрия 10-11 кл. – М.: Просвещение, 2014. Ход работы: Организационный момент: Доброе утро, 10 «А» класс! Давайте отметим, кто сегодня отсутствует. Актуализация знаний: Устный вопрос: Слайд 1. Давайте откроем тетради, запишем число, классную работу и темы сегодняшнего занятия: «Взаимное расположение прямых в пространстве. Угол между двумя прямыми». Слайд 2-3. Давайте вспомним взаимное расположение прямой и плоскости. Слайд 4-6. Скрещивающиеся прямые. Примеры. Слайд 7. Определение скрещивающихся прямых. Две прямые называются скрещивающимися, если они не лежат в одной плоскости. Слайд 8-9.   Разберем и докажем еще одну теорему о скрещивающихся прямых. Слайд 10. Теорема. Теорема. Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна. 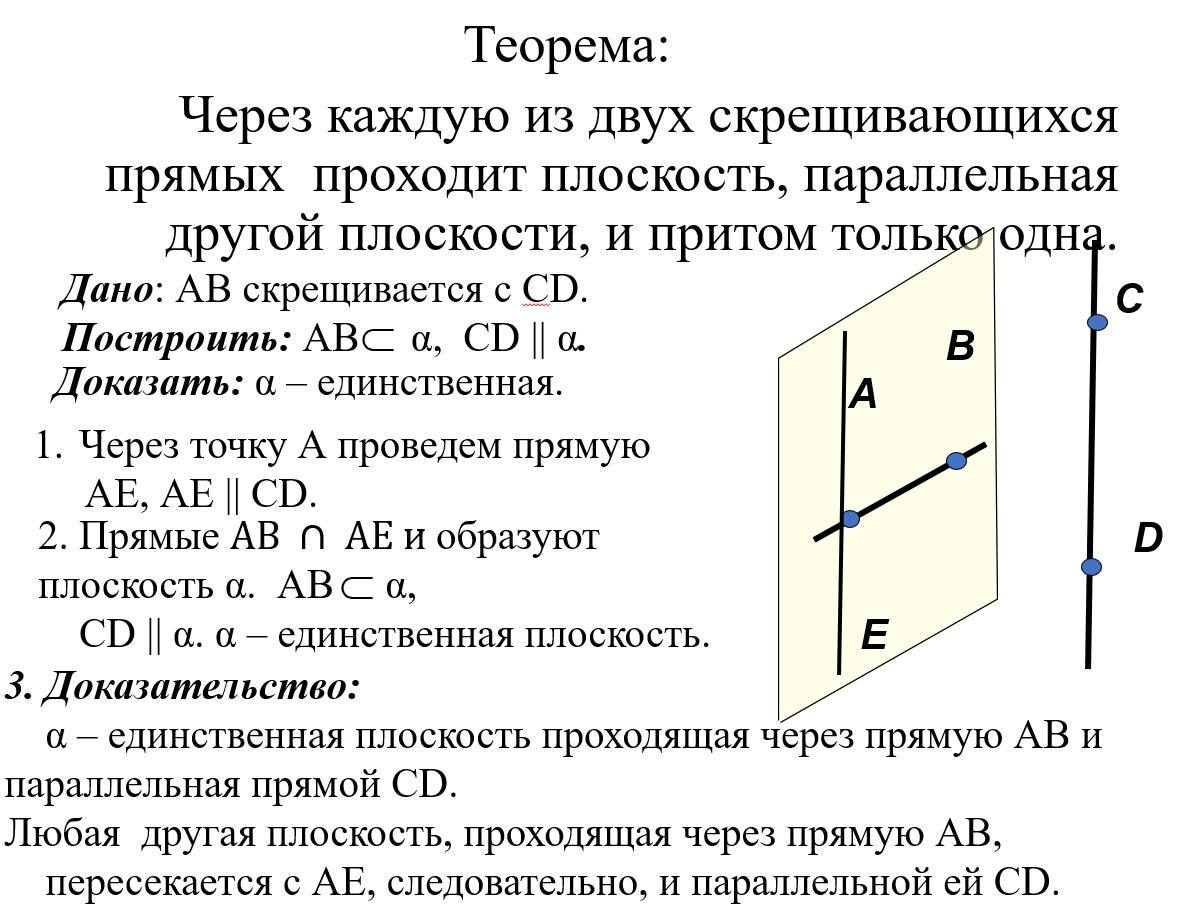 Слайд 11-12. Задача 34 Слайд 13. Углы с сонаправленными сторонами Слайд 14. Любая прямая а, лежащая в плоскости, разделяет эту плоскость на две части, называемые полуплоскостями. Прямая a называется границей каждой из этих полуплоскостей.  Слайд 15. Сонаправленные углы. 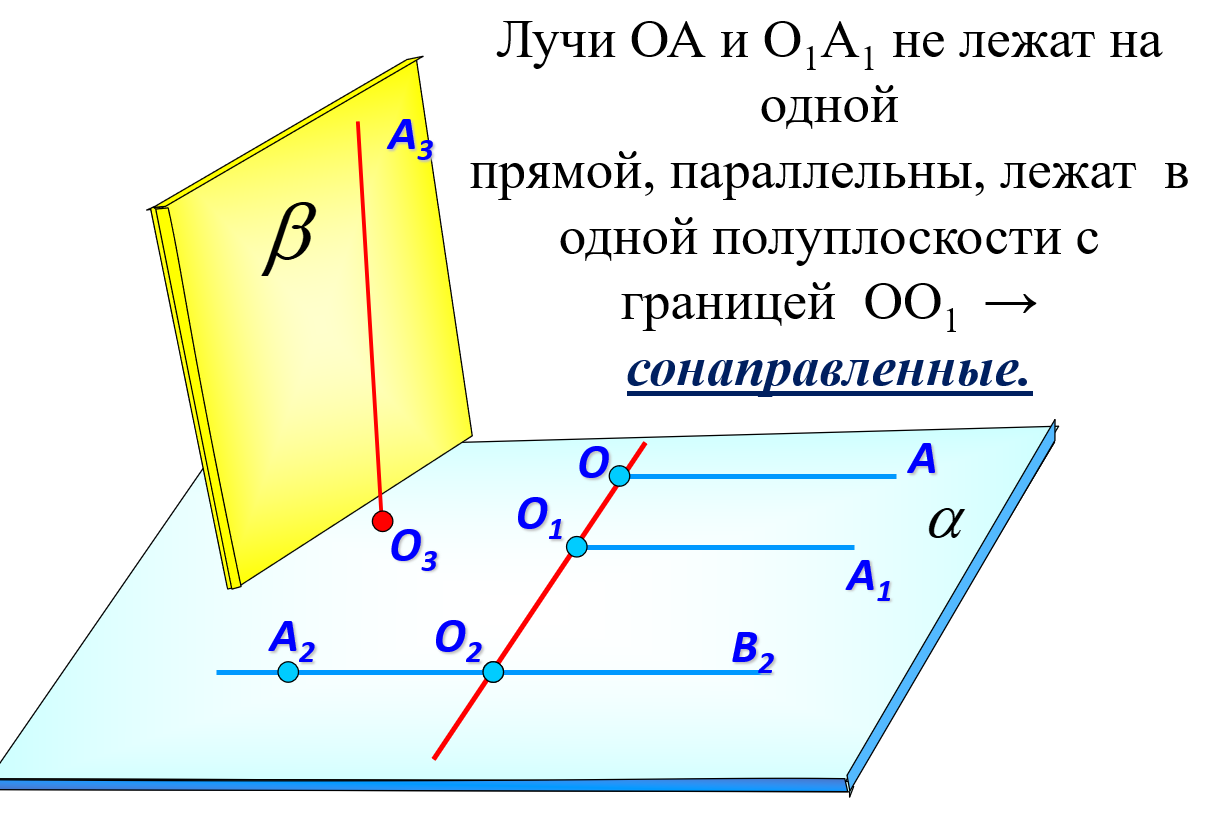 Любая прямая, например ОО1, рассекает плоскость на две полуплоскости. Если лучи ОА и О1А1 параллельны и лежат в одной полуплоскости, то они называются сонаправленными. Лучи О1А1 и ОА не являются сонаправленными. Они параллельны, но не лежат в одной полуплоскости. (рис. 4) Слайд 16. Теорема. Если стороны двух углов соответственно сонаправленны, то такие углы равны.   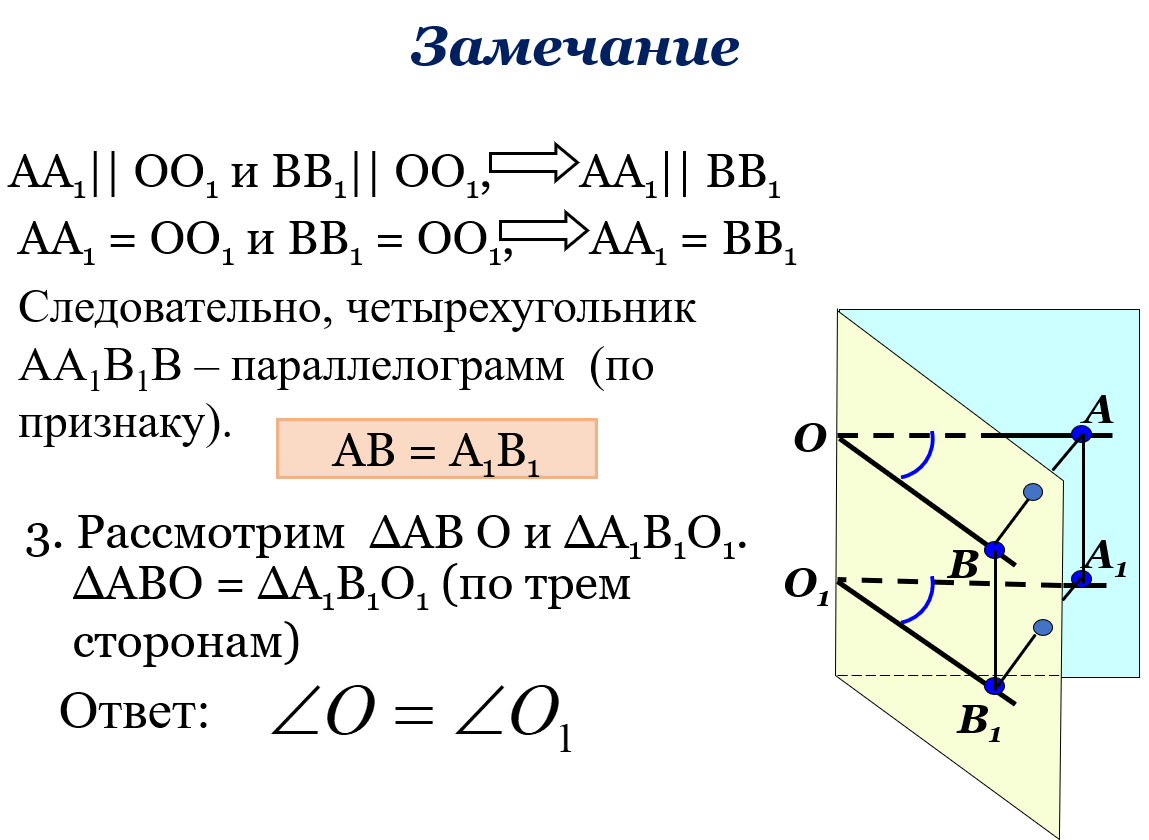 Слайд 19. Любые две пересекающиеся прямые лежат в одной плоскости и образуют четыре неразвернутых угла. Если известен один из этих углов, то можно найти и другие три угла. Пусть а - тот из углов, который не превосходит любого из трех остальных углов. Тогда говорят, что угол между пересекающимися прямыми равен а. Очевидно, 0° < а ≤ 90°. Введем теперь понятие угла между скрещивающимися прямыми(рис. 6, 7).Пусть АВ и СD- две скрещивающиеся прямые (рис. а.) Через произвольную точку М1 проведем прямые А1В1 и С1D1, соответственно параллельные прямым АВ и СВ (рис. б). Если угол между прямыми А1В1 и C1D1 равен φ, то будем говорить, что угол между скрещивающимися прямыми АВ и CD равен φ. Докажем, что угол между скрещивающимися прямыми не зависит от выбора точки М₁. Действительно, возьмем любую другую точку М₂ и проведем через нее прямые А1В1 и С1D1, соответственно параллельные прямым АВ и СD (рис. б). Так как А1В1||А1В1, C1D1|| С1D1, то стороны углов с вершинами М1 и М1 попарно сонаправлены (рис. б, такими углами являются ∟A1M1C1 и ∟A1M1C1, ∟A1M1D1 и ∟A1M1D1 и т.д.) Поэтому эти углы соответственно равны. Отсюда следует, что угол между прямыми А1В1 и С1D1 также равен φ. В качестве точки М, можно взять любую точку на одной из скрещивающихся прямых. На рисунке в на прямой СD отмечена точка М и через нее проведена прямая А'В', параллельная АВ. Угол между прямыми А'В' и СD также равен φ.  Рисунок 6 – угол между скрещивающимися прямыми  Рисунок 7 – угол между скрещивающимися прямыми |
