открытый урок. Взаимное расположение прямой и окружности

• Название: Взаимное расположение прямой и окружности
• Дата: 19.04.2023
• Размер: 1.2 Mb.
• Имя файла: открытый урок.doc
• Тип: Урок; #1074346

Открытый урок по геометрии 8 класс.

Тема: Взаимное расположение прямой и окружности.

Учитель: __________________________________Зудина Ирина Эдуардовна

ГБОУ СОШ №2014

Взаимное расположение прямой и окружности

Цели урока:

1. Рассмотреть различные случаи взаимного расположения прямой и окружности.

2. Ввести понятия касательной, точке касания.

3. Рассмотреть свойство касательной.

4. Совершенствовать навыки решения задач.

Оборудование: Компьютер, проектор, циркули, линейки.

Учебный материал – презентация

На доске план урока:

1. 
   Постановка проблемы
   
2. 
   Актуализация (устная работа)
   
3. 
   Взаимное расположение прямой и окружности (3 случая)
   
4. 
   Определение прямой и окружности
   
5. 
   Свойство касательной
   

1 слайд. Постановка проблемы

Как вы думаете, сколько общих точек могут иметь прямая и окружность?

2 слайд. Актуализация

Сначала вспомним как задаётся окружность

3 слайд. Исследуем взаимное расположение прямой и окружности в первом случае

Вывод: Если расстояние от центра до прямой меньше радиуса окружности, то окружность и прямая имеют две общие точки. Прямая называется секущей.

4 слайд. Второй случай:

Вывод: Если расстояние от центра до прямой равно радиусу окружности, то эта прямая и окружность имеют одну общую точку.

5 слайд. Третий случай:

Вывод: Если расстояние от центра до прямой больше радиуса окружности, то эта прямая и окружность не имеют общих точек.

6 слайд. Сколько общих точек могут иметь прямая и окружность? (Составление опорного конспекта)

7 слайд. Взаимное расположение прямой и окружности, когда они имеют одну общую точку.

Вывод: Прямая называется касательной по отношению к окружности

8 слайд. Свойства касательной.

Вывод: Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.

9 слайд. Даны прямоугольник АВСО, диагональ которого 12 см и угол между диагональю и стороной 30⁰, и окружность с центром в точке О радиуса 5 см. Какие из прямых ОА, АВ, ВС и АС являются секущими по отношению к этой окружности?

Решение: ОА-секущая, АВ,ВС и АС не являются секущими.

10 слайд. № 633 Даны квадрат АВСО, сторона которого 6 см, и

окружность с центром в точке О радиуса 5 см. Какие из прямых ОА, АВ, ВС и АС являются секущими по отношению к этой окружности?

Решение: ОА,АС – секущие, АВ и ВС не являются секущими.

11 слайд. № 634 Радиус ОМ окружности с центром О делит хорду АВ пополам. Докажите, что касательная, проведенная через точку М, параллельна хорде АВ.

Решение: Соединим А и В с центром ОА=ОВ как радиусы. Треугольник АОВ- равнобедренный. OF – высота, угол OFB=90 градусов. PN- касательная и перпендикулярна радиусу, угол ОМN=90 градусов. АВ||PN

12 слайд. № 635 Через точку А окружности проведены касательная и хорда, равная радиусу окружности. Найдите угол между ними.

Решение: Треугольник ОАВ – равносторонний. Углы равностороннего треугольника равны 60 градусам. Угол ОАN=90 градусов, угол ВАN=90-60=30

13 слайд. № 636 Через концы хорды АВ, равной радиусу окружности, проведены две касательные, пересекающиеся в точке С. Найдите угол АСВ.

Решение: треугольник ОАВ- равносторонний, углы 60 градусов. Угол ОАС = 90

- свойства касательной. Угол ВАС=90-60=30. Угол АВО=60. Угол ОВА=90. Угол АВС=90-60=30. Угол АВС=180-(30+30)=120

14 слайд. № 637 Угол между диаметром АВ и хордой АС равен 30⁰. Через точку С проведена касательная, пересекающая прямую АВ в точке D. Докажите, что треугольник АСD равнобедренный.

Решение. Треугольник АОС – равнобедренный, А=С=30. Угол ОСД=90, Угол АСД=90+30=120, Угол АДС=180-150=30.Угол ОАС=АДС=30, углы при основании равны, треугольник АСД- равнобедренный.

Итог урока: Сколько общих точек могут иметь прямая и окружность, и от чего это зависит. Какая прямая называется касательной к окружности и каким свойством она обладает.

Домашнее задание: П.68, 69 №638, 639.

Как вы думаете, сколько общих точек может иметь прямая и окружность?



Сначала вспомним, как задается окружность.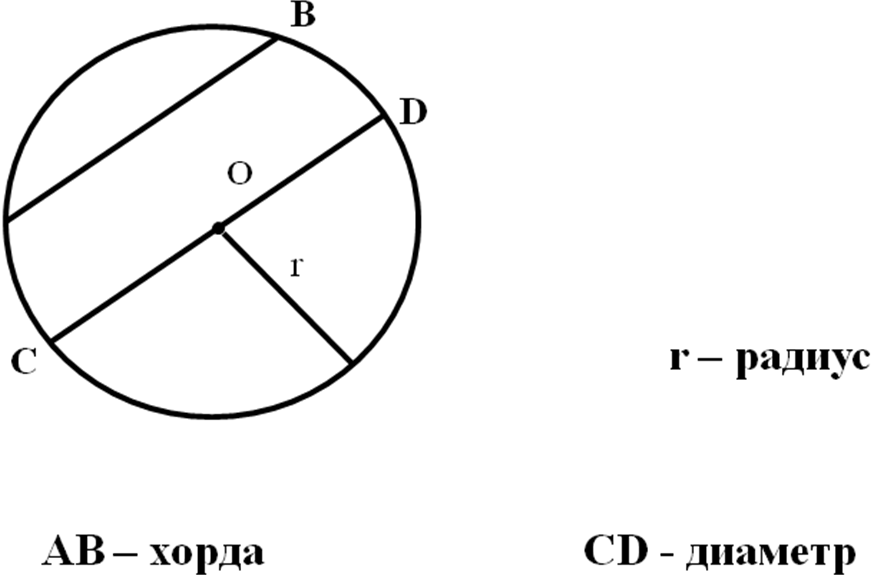



Исследуем взаимное расположение прямой и окружности в первом случае: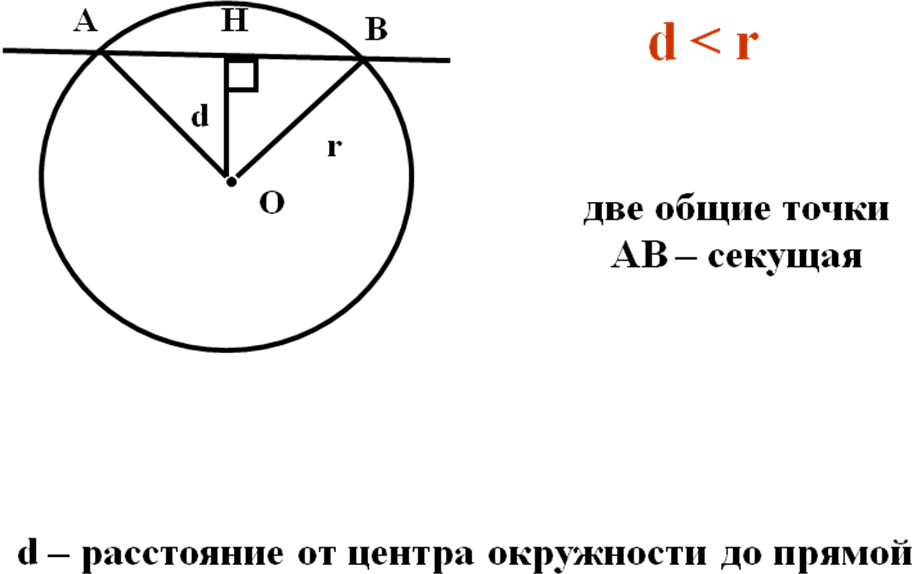



Второй случай:



Третий случай:



Сколько общих точек могут иметь прямая и окружность?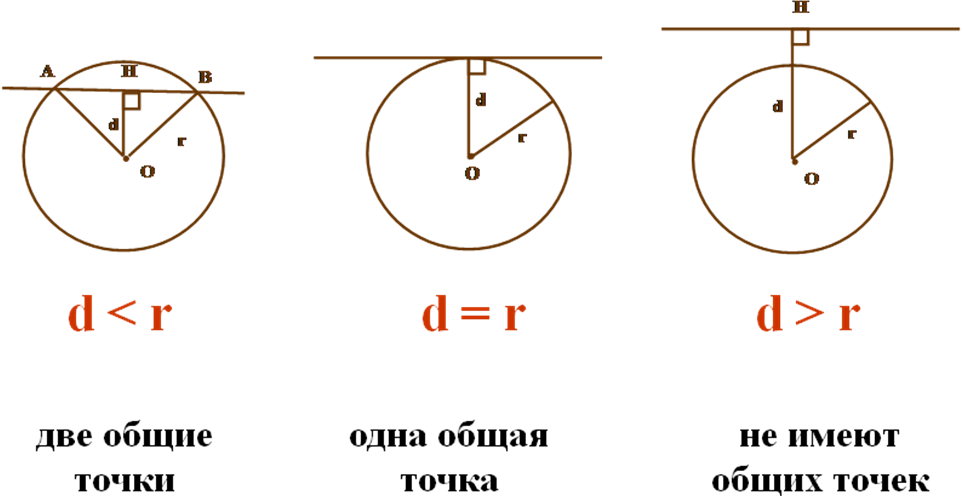



Взаимное расположение прямой и окружности.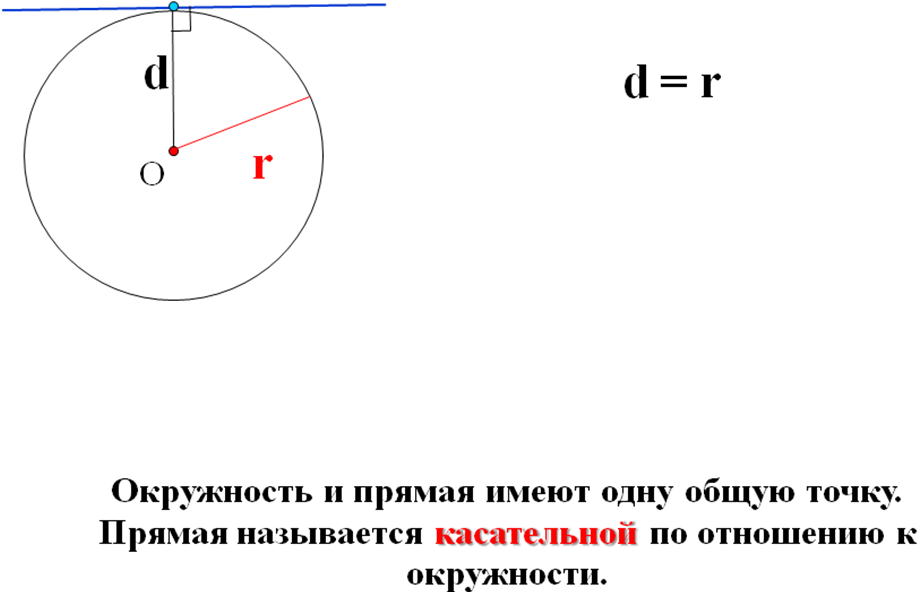



Свойства касательной.



Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.

Даны прямоугольник АВСО, диагональ которого 12 см и угол между диагональю и стороной 30⁰, и окружность с центром в точке О радиуса 5 см. Какие из прямых ОА, АВ, ВС и АС являются секущими по отношению к этой окружности?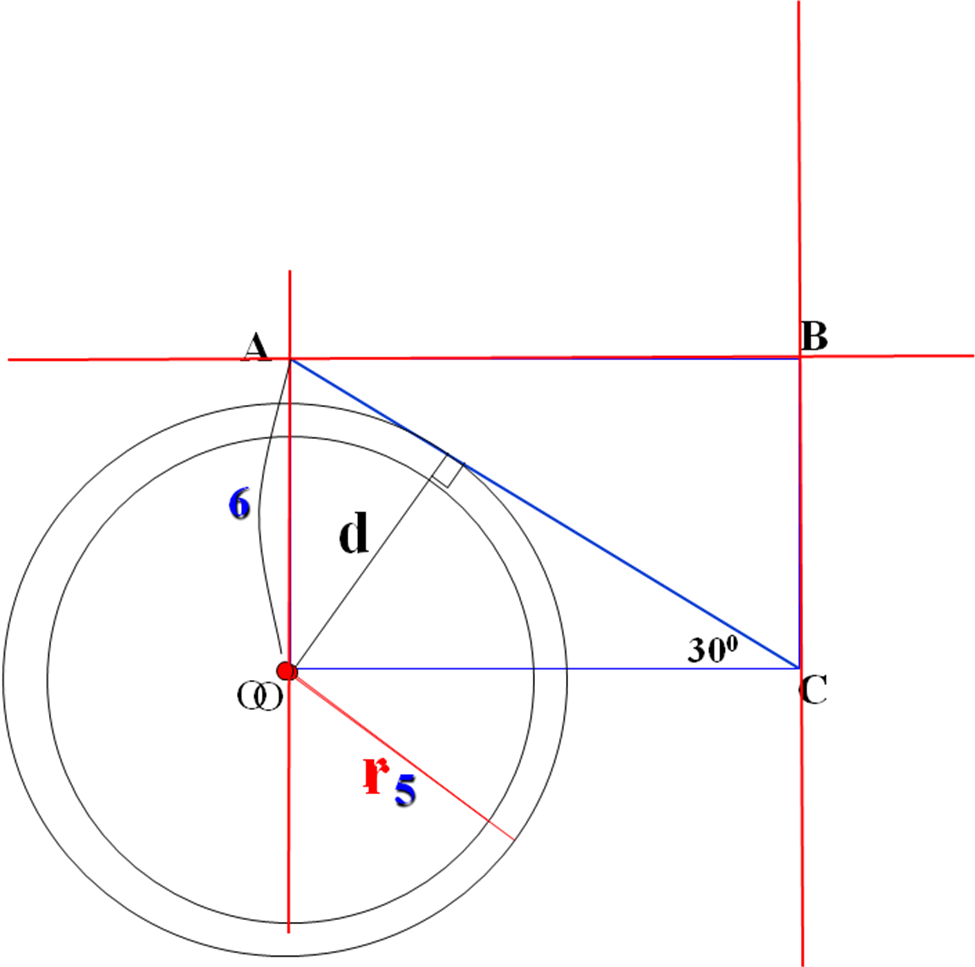



№633 Даны квадрат АВСО, сторона которого 6 см, и окружность с центром в точке О радиуса 5 см. Какие из прямых ОА, АВ, ВС и АС являются секущими по отношению к этой окружности?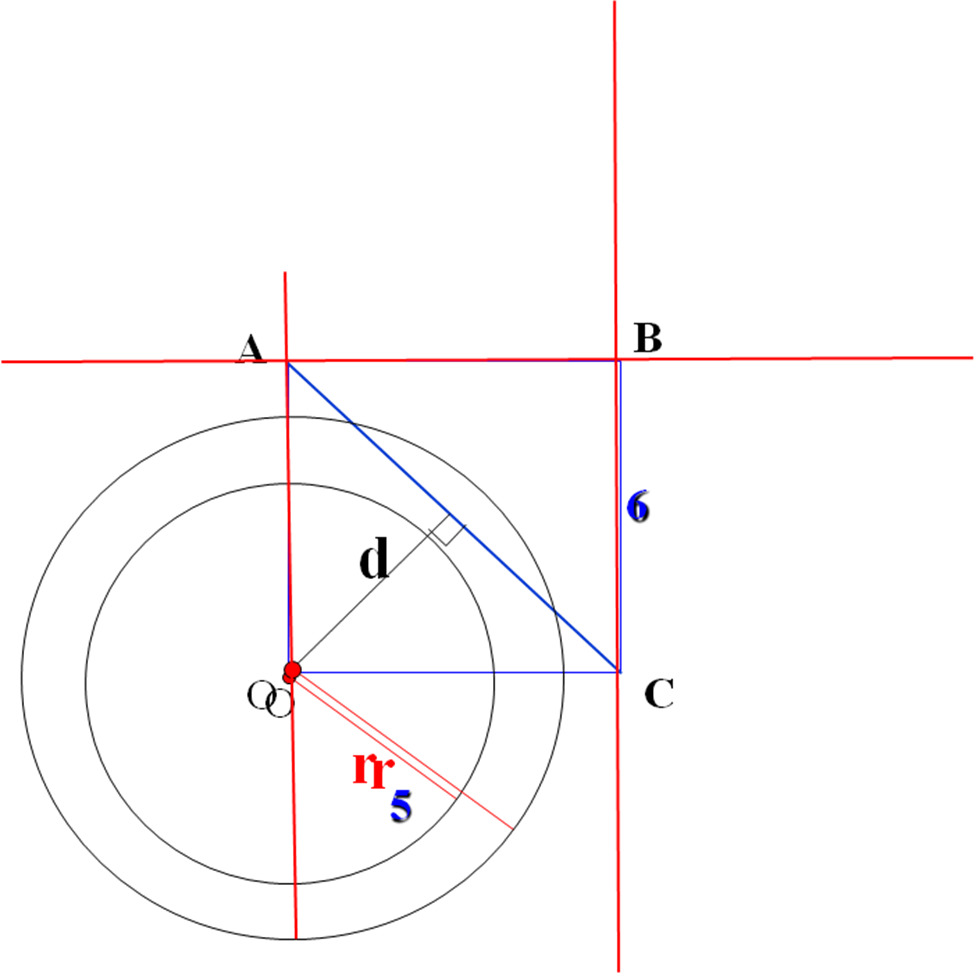



№634 Радиус ОМ окружности с центром О делит хорду АВ пополам. Докажите, что касательная, проведенная через точку М, параллельна хорде АВ.



№635 Через точку А окружности проведены касательная и хорда, равная радиусу окружности. Найдите угол между ними.



№636 Через концы хорды АВ, равной радиусу окружности, проведены две касательные, пересекающиеся в точке С. Найдите угол АСВ.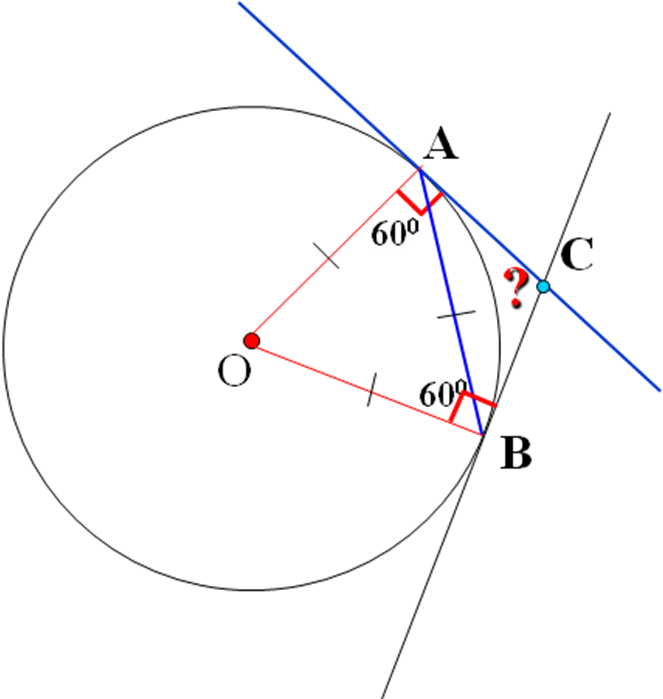



№637 Угол между диаметром АВ и хордой АС равен 30⁰. Через точку С проведена касательная, пересекающая прямую АВ в точке D. Докажите, что треугольник АСD равнобедренный.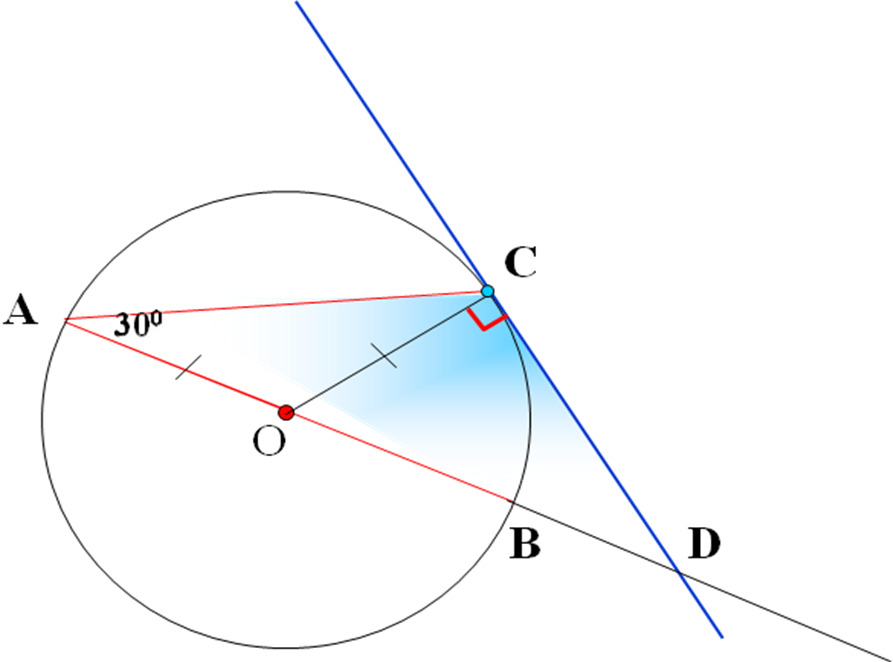



№638 Прямая АВ касается окружности с центром О радиуса r в точке В. Найдите АВ, если ОА = 2 см, а r = 1,5 см.



№639 Прямая АВ касается окружности с центром О радиуса r в точке В. Найдите АВ, если угол АОВ равен 60⁰, а r = 12 см.



Список литературы:

1. Геометрия 7-9. Л.С.Атанасян. под редакцией Л.С.Атанасяна. – М.:Просвящение, 2004.

2. Н.Б. Мельникова и др. Геометрия: Дидактические материалы 7-9 кл. Учебное пособие. М.: Мнемозина, 1997-272с.