Основы корреляционного анализа. X у x у x у x у

• Название: X у x у x у x у
• Анкор: Основы корреляционного анализа
• Дата: 07.01.2021
• Размер: 383.39 Kb.
• Имя файла: Основы корреляционного анализа.docx
• Тип: Документы; #166213

10. Основы корреляционного анализа
Задание

Вычислите коэффициент корреляции между числом эритроцитов (млн.) и содержанием гемоглобина (%) по 36 анализам крови; х - число эритроцитов, у - содержание гемоглобина.

X У X У X У X У

0,80 22 3,46 77 3,71 97 3,30 82

1,71 45 3,32 80 4,22 96 4,10 81

2,63 61 3,11 82 3,90 92 3,29 82

3,19 66 3,28 79 4,36 94 3,81 87

2,80 72 3,66 84 2,50 50 4,20 87

3,14 83 3,90 75 1,30 27 4,47 90

3,21 73 4,33 82 2,80 63 3,68 72

3,28 82 3,80 79 3,10 71 3,59 76

3,63 78 3,82 87 2,87 70 3,40 71

Построите корреляционную решетку по данным выше и проведите разноску материала в табл. 1. Посчитайте клетки (под знаком?). Вычислите коэффициент корреляции, его ошибку и критерий достоверности.

По одному внешнему виду расположения частот в корреляционном поле, не вычисляя r, можем делать приблизительное заключение о степени корреляции: чем ближе частоты расположены к диагонали решетки, тем сильнее корреляция.

Таблица 1 – Для заполнения данных (?)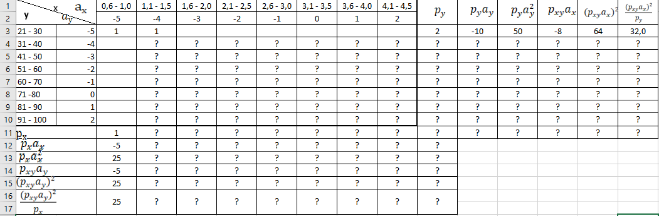



Примечание. Последние три графы ( , и их производные) понадобяться в дальнейшем ( при вычислении корреляционного отношения).
Рабочая формула, с помощью которой вычисляют коэффициент корреляции, следующая: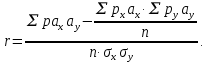


Для того чтобы подставить в нее все необходимые значения, надо сначала вычислить показатель 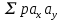. Это делается перемножением показателей для каждой клетки решетки, кроме условно средних классов (с помощью метода квадратов):p_xy·a_x·a_y= pa_xa_y, т. е. частоты (p_xy) каждой клетки корреляционной решетки умножаются на соответствующие отклонения классов, (или классовых вариант) сначала одного, а затем другого вариационного рядов. Полученные результаты записываются по квадратам и суммируются ( ).

I квадрат	II квадрат	III квадрат	IV квадрат
1 · (-5) · (-5) = 25	0	0	4 · 1 · 1 = 4
1 · (-4) · (-5) = 20			4 · 2 · 1 = 8
1 · (-3) · (-3) = 9			2 · 1 · 2 = 4
1 · (-2) · (-3) = 6			2 · 2 · 2 = 8
3 · (-1) · (-1) = 3			+24
+63

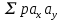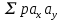представляет собой суммирование по всем четырем квадратам и в данном случае равняется 87 (63 + 0 + 0 + 24).

Далее необходимо установить значение σ_х и σ_y. Причем при вычислении сигм для нахождения коэффициента корреляции интервал (i) опускается, так как он не влияет на взаимосвязь. В данном случае формула принимает вид: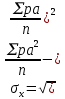



Для каждого полученного коэффициента корреляции должна быть вычислена его ошибка и через нее - показатель достоверности. При этом в случае больших выборок (n>100) и при не очень высоком коэффициенте корреляции среднюю ошибкудля r можно вычислить по формуле: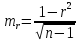

,

а критерий достоверности: .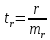

Для малых же выборок (при изучениисвязей, когда n<100) формулы иные: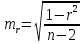

, а критерий достоверности:

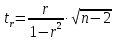Далее необходимо определить по табл. 2 степень достоверности и уровень значимости критерия t (для малого числа наблюдений n).
Таблица 2 – Площадь кривой вероятности по Стьюденту в пределах ±t для малого числа наблюдений n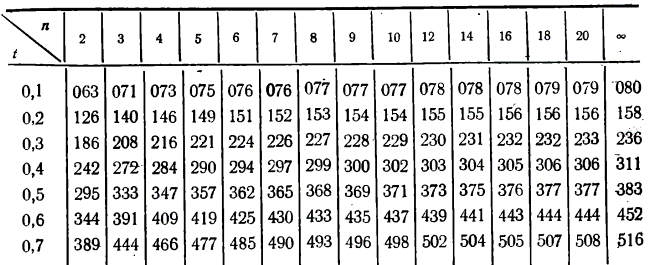





В случае же больших выборок (n>100) критерий достоверности оценивается обычным способом при трех уровнях доверительной вероятности (табл. 3):

при вероятности 0,95 t=1,96;

при вероятности 0,99 t=2,58;

при вероятности 0,999 t= 3,30.
Таблица 3 – Значения t при различных уровнях значимости (Р)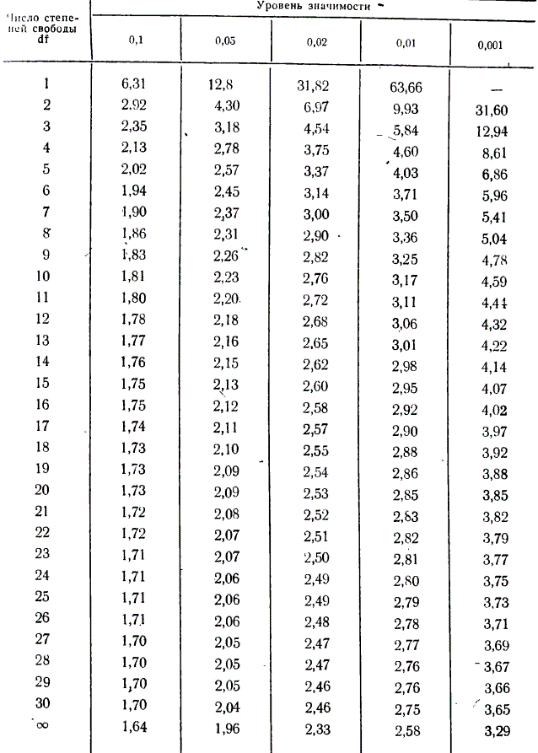



Кроме того, можно оценить достоверность коэффициента корреляции и не прибегая к вычислению ошибки и последующему обращению к таблице распределения t. Для этого служит специальная табл. 4, с помощью которой легко определить достоверность r при разных n непосредственно по значению коэффициента корреляции. Чтобы полученный коэффициент корреляции можно было считать достоверным, он должен превышать табличное значение при данном n.

Таблица 4 - Необходимые значения коэффициента корреляции r при различных уровнях значимости Р и разных n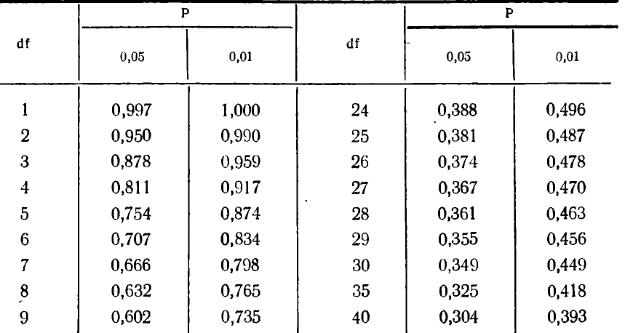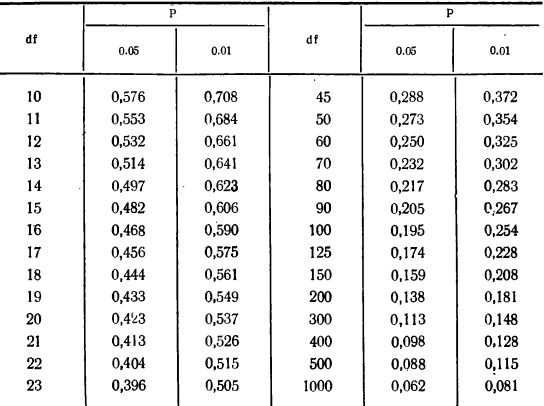





Для того чтобы пользоваться данной таблицей, необходимо иметь представление о так называемом числе степеней свободы (df). Обычно при численности выборки (членов совокупности), равной n, число степеней свободы df = n-1, что, естественно может иметь значение лишь для малых выборок (при большом n разница между этим числом и им же, уменьшенным на единицу, настолько невелика, что ею вполне можно пренебречь). Лишь в некоторых случаях, например при пользовании критерием хи-квадрат, а также при корреляционных сопоставлениях, число степеней свободы вычисляется более сложно. Однако, не вдаваясь в детали, можно определить величину df, используемую для оценки коэффициента корреляции, как n-2, т. е. число сопряженных пар, уменьшенное на две единицы.