З в І т з лабораторної роботи 15 схеми ймовірнісного шифрування варіант 6
 Скачать 340.09 Kb. Скачать 340.09 Kb.
|
|
Державний університет телекомунікацій Навчально-науковий інститут захисту інформації Кафедра інформаційної та кібернетичної безпеки Прикладна криптологія З В І Т з лабораторної роботи № 15 СХЕМИ ЙМОВІРНІСНОГО ШИФРУВАННЯ Варіант № 6 Виконав(ла): студент(ка) групи БСД-32Прізвище І.Б Голух Д.Р Дата здачі/захисту____________________ Перевірив__________________________ Оцінка_____________________________ 2018Виконання роботи Завдання 1. В криптосистемі Блюма-Гольдвассер 1) Вибрати довільний відкритий текст (на англійській, російській або українській мовах), записати у бітовому представленні відповідно до номерів букв у нормативному алфавіті. Розв’язання. Виберемо для шифрування відкритий текст «дзвонар». Представимо шифроване повідомлення як послідовність цілих чисел, для цього кожну букву відкритого тексту замінимо її номером в українському алфавіті (тобто а–00, б–01,…, я–32, пробіл – 33), а потім запишемо в двійковій формі:
Отже 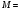 000011 001111 001100 010100 010110 000011 001111 001100 010100 010110Довжина повідомлення 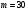 біта, тому для зашифрування потрібно згенерувати ключову псевдовипадкову послідовність біта, тому для зашифрування потрібно згенерувати ключову псевдовипадкову послідовність 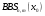 з 30 випадкових бітів. з 30 випадкових бітів.2) Для вибраного тексту згенерувати ключову псевдовипадкову послідовність 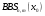 за допомогою генератора BBS по елементах закритого ключа, вибравши двозначні прості числа за допомогою генератора BBS по елементах закритого ключа, вибравши двозначні прості числа 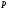 і і 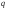 з першої сотні. з першої сотні.Розв’язання. Згенеруємо ключову псевдовипадкову послідовність 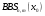 за допомогою генератора BBS: за допомогою генератора BBS:
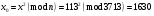 . .
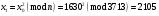 ; ;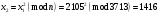 ; ;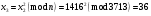 ; ;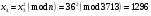 ; ;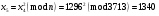 ; ;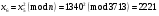 ; ;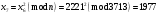 ; ;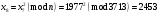 ; ;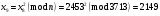 ; ;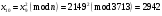 ; ;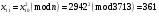 ; ;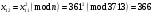 ; ;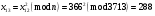 ; ;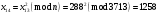 ; ;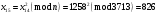 ; ;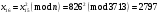 ; ;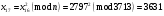 ; ;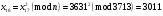 ; ;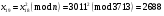 ; ;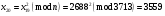 ; ;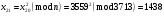 ; ;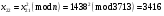 ; ;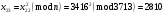 ; ;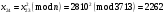 ; ;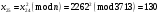 ; ;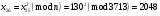 ; ;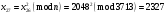 ; ;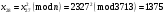 ; ;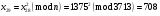 ; ;
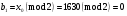 ; ;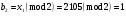 ; ;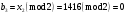 ; ;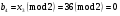 ; ;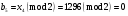 ; ;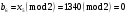 ; ;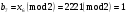 ; ;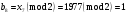 ; ;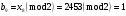 ; ;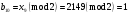 ; ;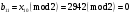 ; ;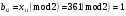 ; ;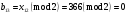 ; ;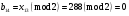 ; ;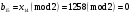 ; ;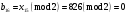 ; ;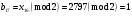 ; ;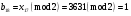 ; ;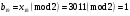 ; ;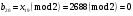 ; ;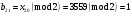 ; ;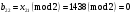 ; ;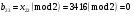 ; ;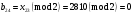 ; ;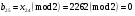 ; ;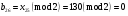 ; ;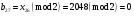 ; ;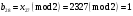 ; ;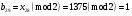 ; ;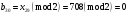 ; ;. Отже, 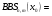 010000 111101 000011 101000 000110. 010000 111101 000011 101000 000110.3) Зашифрувати відкритий текст. Розв’язання. Зашифруємо текст за формулою 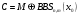 : : 000011 001111 001100 010100 010110 000011 001111 001100 010100 010110  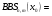 010000 111101 000011 101000 000110 010000 111101 000011 101000 000110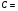 010011 110010 001111 111100 010000 010011 110010 001111 111100 010000Шифроване повідомлення (криптограма) складається з пари 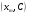 : :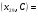 (708, 010011 110010 001111 111100 010000) (708, 010011 110010 001111 111100 010000)4) Розшифрувати отриманий шифртекст. Розв’язання. Розшифруємо отриманий шифртекст за відомими елементами закритого ключа 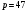 і і 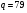 . Визначимо параметр . Визначимо параметр 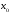 з отриманого в криптограмі значення з отриманого в криптограмі значення 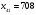 (нумерація чисел в послідовності починається з 0, тому (нумерація чисел в послідовності починається з 0, тому 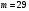 ). Для цього: ). Для цього:1. Застосувавши до чисел 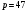 і і 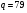 розширений алгоритм Евкліда, знайдемо цілі числа розширений алгоритм Евкліда, знайдемо цілі числа  і і 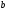 , при яких , при яких 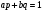 : : 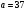 , , 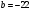 . .2. Знайдемо лишки 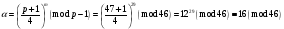 ; ;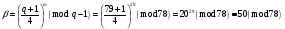 ; ;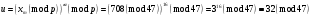 ; ;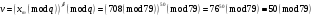 . .3. Тоді 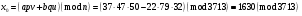 . .Отримане значення 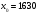 збігається з використаним в роботі генератора BBS при шифруванні. Тому далі визначимо всі члени послідовності збігається з використаним в роботі генератора BBS при шифруванні. Тому далі визначимо всі члени послідовності 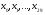 =1630, 2105,…., 708 і відновимо двійковий вектор =1630, 2105,…., 708 і відновимо двійковий вектор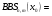 001000 100100 101001 100100 100001 010011 011001. 001000 100100 101001 100100 100001 010011 011001.Розшифруємо криптограму 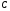 за формулою за формулою 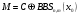 : :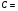 010011 110010 001111 111100 010000 010011 110010 001111 111100 010000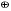 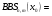 010000 111101 000011 101000 000110 010000 111101 000011 101000 000110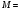 000011 001111 001100 010100 010110 000011 001111 001100 010100 010110Переходячи до десяткового запису, а потім, замінюючи цифровий еквівалент відповідною буквою, отримаємо початкове відкрите повідомлення:
Завдання 2. В криптосистемі Гольдвассер- Мікалі 1) Згенерувати ключі, вибравши двозначні прості числа 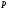 і і 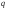 з першої сотні. з першої сотні.Розв’язання. Згенеруємо ключі, для чого
3. З мультиплікативної групи лишків 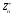 випадково виберемо інше ціле число випадково виберемо інше ціле число 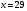 , взаємно просте з числом Блюма , взаємно просте з числом Блюма 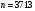 : : 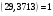 і таке, що і таке, що 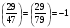 . .4. Відкритий ключ ― пара (3713, 29), закритий ключ ― (47, 79). 2) Зашифрувати довільне повідомлення (на англійській, російській або українській мовах). Розв’язання. Зашифруємо повідомлення «дзвін». Представимо шифроване повідомлення як послідовність цілих чисел, для цього кожну букву відкритого тексту замінимо її номером в українському алфавіті (тобто а–00, б–01,…, я–32, пробіл – 33), а потім запишемо в двійковій формі:
Отже, 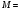 000100 001001 001101 000000. 000100 001001 001101 000000.Біт шифрованого тексту обчислюємо за бітом відкритого тексту за формулою 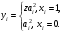 , ,де ai – випадкове число з Zn. 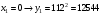 , , 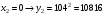 , ,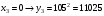 , ,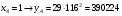 , ,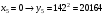 , ,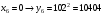 , ,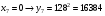 , , 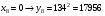 , ,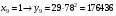 , ,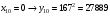 , ,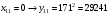 , ,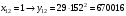 , ,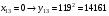 , ,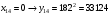 , ,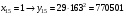 , ,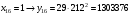 , ,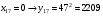 , ,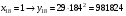 , ,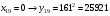 , ,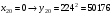 , ,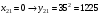 , ,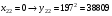 , ,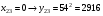 , ,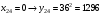 , ,3) Розшифрувати отриманий шифртекст. Розв’язання. Розшифруємо отриманий шифртекст. Біт відкритого тексту обчислюємо за бітом шифрованого тексту за формулою 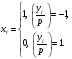 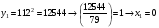 , , 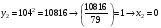 , ,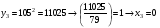 , ,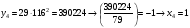 , ,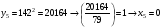 , ,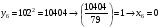 , ,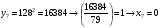 , , 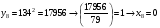 , ,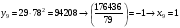 , ,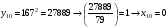 , ,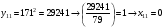 , ,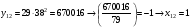 , ,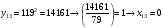 , ,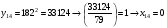 , ,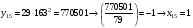 , ,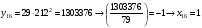 , ,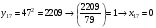 , ,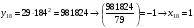 , ,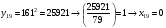 , ,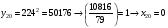 , ,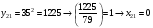 , ,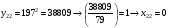 , ,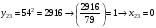 , ,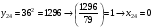 , ,Отже, 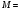 000100 001001 001101 000000. 000100 001001 001101 000000.Переходячи до десяткового запису, а потім, замінюючи цифровий еквівалент відповідною буквою, отримаємо початкове відкрите повідомлення:
|

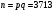 .
.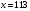 , взаємно просте з числом Блюма
, взаємно просте з числом Блюма 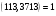 .
.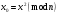 , яке буде початковим значенням генератора:
, яке буде початковим значенням генератора: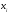 згідно із законом
згідно із законом 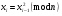 :
: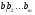 буде послідовність молодших бітів чисел
буде послідовність молодших бітів чисел 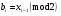 ,
, 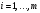 . Обчислюємо:
. Обчислюємо: