КР ТОАиТ Соколов. Забайкальский институт железнодорожного транспорта филиал федерального государственного бюджетного образовательного учреждения высшего образования Иркутский государственный университет путей сообщения
 Скачать 1.63 Mb. Скачать 1.63 Mb.
|
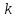 разрядов. Минимальное число разрядов. Минимальное число 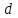 элементов, в которых одна кодовая комбинация двоичного кода отличается от другой (по всем парам кодовых комбинаций) называется кодовым расстоянием данного кода. В помехозащищенных кодах, позволяющих обнаружить факт искажения принимаемых кодовых комбинаций при наличии элементов, в которых одна кодовая комбинация двоичного кода отличается от другой (по всем парам кодовых комбинаций) называется кодовым расстоянием данного кода. В помехозащищенных кодах, позволяющих обнаружить факт искажения принимаемых кодовых комбинаций при наличии 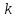 и менее любых ошибок, кодовое расстояние между всеми парами используемых (входящих в число разрешенных) кодовых комбинаций должно быть на 1 больше числа ошибок, т.е.: d ≥ k + 1. Очевидно, что в этом случае искаженная кодовая комбинация (входящая в состав запрещенных для использования комбинаций) будет отличаться от любой разрешенной кодовой комбинации хотя бы в одном разряде, и благодаря этому обнаруживаться. Поэтому принцип обнаружения ошибок при декодировании заключается в проверке минимального кодового расстояния dmin принятой кодовой комбинации по отношению к разрешенным, оно должно быть не менее кодового расстояния разрешенных комбинаций:. dmin ≤ d Кодовое расстояние между двумя любыми комбинациями легко определяется путем подсчета числа единиц, получаемых при сложении этих комбинаций по модулю 2 ( и менее любых ошибок, кодовое расстояние между всеми парами используемых (входящих в число разрешенных) кодовых комбинаций должно быть на 1 больше числа ошибок, т.е.: d ≥ k + 1. Очевидно, что в этом случае искаженная кодовая комбинация (входящая в состав запрещенных для использования комбинаций) будет отличаться от любой разрешенной кодовой комбинации хотя бы в одном разряде, и благодаря этому обнаруживаться. Поэтому принцип обнаружения ошибок при декодировании заключается в проверке минимального кодового расстояния dmin принятой кодовой комбинации по отношению к разрешенным, оно должно быть не менее кодового расстояния разрешенных комбинаций:. dmin ≤ d Кодовое расстояние между двумя любыми комбинациями легко определяется путем подсчета числа единиц, получаемых при сложении этих комбинаций по модулю 2 (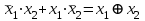 ). ). Путем сложения по модулю 2 принятой комбинации с разрешенными можно определить ее истинность или ложность. Первая имеет место, если результат сложения нулевой, а последняя - если, хотя бы в одном из разрядов полученной суммы имеется единичное значение. К числу кодов с обнаружением ошибок относится инверсный код (код Бауэра), представляющий собой разновидность кода с повторением, в котором в качестве контрольных разрядов повторяются разряды исходного кода, при этом общее число разрядов полученной кодовой комбинации увеличивается вдвое. Код Бауэра отличается от кода с повторением тем, что при нечетной сумме единиц в исходной комбинации, ее проверочная часть, содержащая контрольные разряды инвертируется, а при четной сумме единиц - проверочная часть кода с повторением остается неизменной. Например, исходная 3-х разрядная кодовая комбинация 010 при использования кода с повторением преобразуется к виду: 010 010, а при использовании кода Бауэра имеет вид: 010 101, так как исходная кодовая комбинация содержит нечетное число единиц и, следовательно, проверочная часть кода с повторением (три младших контрольных разряда) инвертируется. Модифицированный код Бауэра является одной из разновидностей кода с повторением и отличается от последнего тем, что при нечетном количестве единиц в исходном коде инвертируются первые (n - 1) разрядов контрольной части инверсного кода, а при четном – только последний разряд инверсного кода. Так, например, при использовании восьмиразрядного модифицированного кода Бауэра кодовая комбинация кода с повторением 1011 1011 преобразуется в кодовую комбинацию 1011 0101, а кодовая комбинация 1001 1001 – в кодовую комбинацию 1001 1000. Особенность этого кода заключается в том, что данный код не имеет комбинаций с одними нулями или единицами, что дает возможность проверять канал связи. Кроме того, данный код является самосинхронизирующимся кодом, при котором любой циклический сдвиг его комбинации не приводит к ложному появлению разрешенных комбинаций. Модифицированный код Бауэра имеет те же характеристики, что и инверсный код. - избыточность кода: R = r/(n+r)=0.5; - минимальное кодовое расстояние: dmin = 4 при n = 4; - число обнаруживаемых ошибок: k = dmin – 1; - число исправляемых ошибок: s = 1 при dmin = 3. Аналитические выражения для определения значений контрольных разрядов кодирующим устройством имеют вид, аналогичный для инверсного кода за исключением младшего разряда. Для 8-ми разрядного модифицированного кода Бауэра (n = r = 4)они принимают следующий вид:
Значения разрядов синдрома кодовой комбинации для ее декодирования определяются по формулам:
Если комбинация значений разрядов синдрома принятой кодовой комбинации равна нулю i0 = 0; i1 = i2 = i3 = 0, значит она принята без ошибок. Наличие единичных значений синдрома, как и в случае применения инверсного кода, свидетельствуют о наличии ошибок: единичное значение только в одном из разрядов - ошибка в соответствующем контрольном разряде, который присутствует в уравнении разряда с единичным значением; три единичных значения - ошибка в соответствующем информационном разряде, значение которого не присутствует в разряде синдрома с нулевым значением; два или четыре единичных значений в синдроме - ошибка в двух и более разрядах. Модифицированный код Бауэра нашел широкое применение в устройствах железнодорожной автоматики и телемеханики. Например, при передаче информации по каналам АЛС-ЕН в устройствах КЛУБ (комплексное локомотивное устройство безопасности), а также в унифицированной микропроцессорной системе автоматической блокировки АБ-УЕ. 2.1 Структурный синтез кодирующего устройства (кодера) 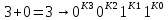 Значения контрольных разрядов в коде Бауэра 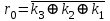 =0 =0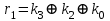 =0 =0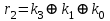 =1 =1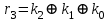 =1 =1Для построения кодирующего устройства необходимо использовать 4 блока 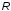 по числу контрольных разрядов. На вход кодирующего устройства подается исходный код 0011, а на выходе имеем кодовую комбинацию 00110010. Для обеспечения синхронизации вывода кода сигналы с блоков R поступают на выход кодера через логические элементы И, на другой вход которых поступает сигнал, инверсный по отношению к синхросигналу, логическая 1 на входы схем И поступает при отсутствии синхросигнала, что исключает возможность изменения состояния последних во время передачи кода. по числу контрольных разрядов. На вход кодирующего устройства подается исходный код 0011, а на выходе имеем кодовую комбинацию 00110010. Для обеспечения синхронизации вывода кода сигналы с блоков R поступают на выход кодера через логические элементы И, на другой вход которых поступает сигнал, инверсный по отношению к синхросигналу, логическая 1 на входы схем И поступает при отсутствии синхросигнала, что исключает возможность изменения состояния последних во время передачи кода.Структурная схема кодера для восьмиразрядного кода Бауэра строится на основе логических формул. Отличие ее от предыдущих схем заключается в том, что число контрольных разрядов равно четырем. Аналогичным образом строится структурная схема кодера для восьмиразрядного кода Бауэра с использованием логической формулы. 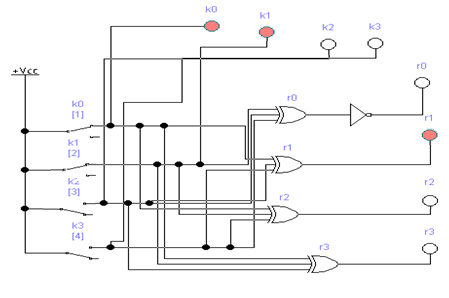  Рисунок 14 – Структурная схема кодера для кода Бауэра 2.2 Структурный синтез декодирующего устройства (декодера) Для построения структурной схемы декодера необходимо использовать полученные ранее логические функции синдромов. Для проверки схемы декодера следует задаться последовательно искажением одного из информационных разрядов и одного из контрольных разрядов и проверить возможность обнаружения и исправления ошибок на основе полученных значений синдромов на выходе декодера. Логическая схема декодера содержит 4 логические схемы I, реализующие функцию сложения по модулю 2 четырех переменных, значение которой однозначно определяет значение соответствующего разряда синдрома. Аналитические выражения для определения значений синдрома декодирующим устройством имеют вид: 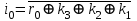 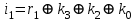 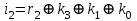 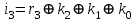 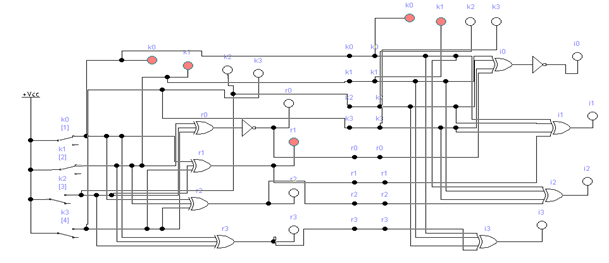 Рисунок 15 – Структурная схема декодера для кода Бауэра 2.3 Исследование корректирующих способностей синтезированного декодера Вводим неисправности: Одиночная ошибка в разряде К1: 0001 1101 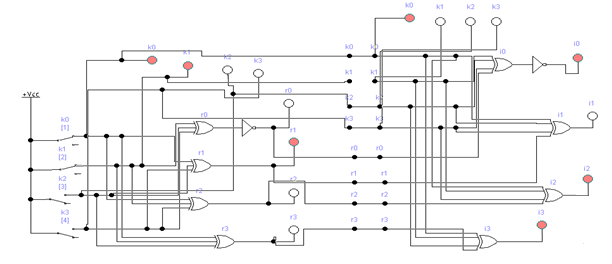 Рисунок 16 - Значения на выходе декодера при ошибке в разряде К1 Одиночная ошибка в разряде К0: 0010 1110 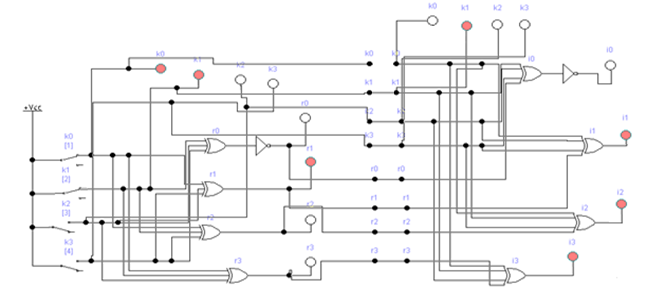 Рисунок 17 - Значения на выходе декодера при ошибке в разряде К0 Одиночная ошибка в разряде r1: 0011 0010 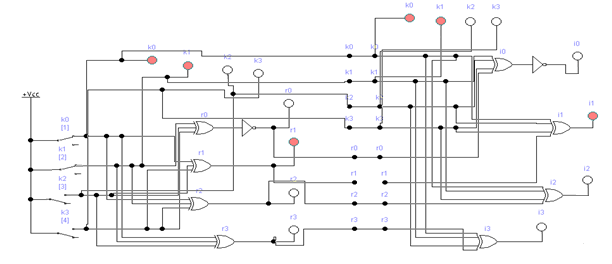 Рисунок 18 - Значения на выходе декодера при ошибке в разряде r1 Двойная ошибка в разрядах r1 и r2: 0011 0010 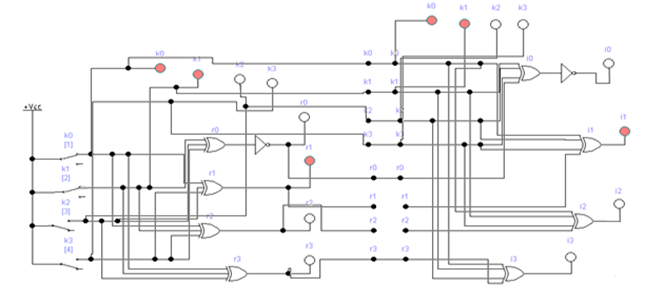 Рисунок 19 - Значения на выходе декодера при ошибке в разрядах r1 и r2 Одиночная ошибка в информационных разрядах плюс одиночная ошибка в контрольных разрядах K0 и r1: 0011 1100 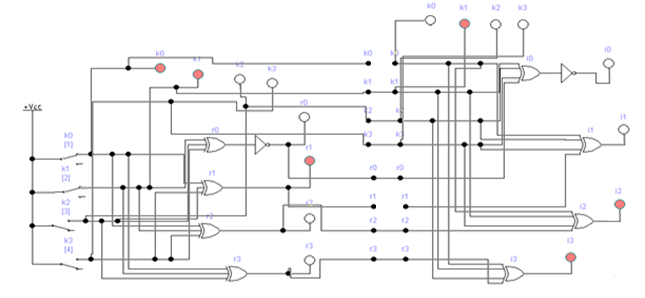 Рисунок 20 - Значения на выходе декодера при ошибке в разрядах К0 и r1 Тройная ошибка в разрядах K0, К1 и r1: 0000 0001 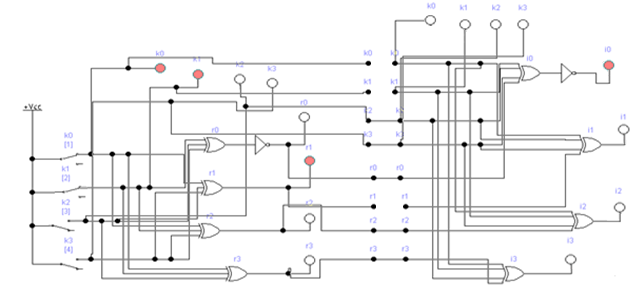 Рисунок 21 - Значения на выходе декодера при ошибке в разрядах K0, K1 и r1 Таблица 2 – Результаты исследований декодера для модифицированного кода Бауэра
Вывод: По результатам исследований корректирующих способностей синтезированного декодера для модифицированного кода Бауэра видно, что данный код позволяет одновременно обнаруживать и исправлять двойные и одиночные ошибки. Заключение В курсовой работе была построена структурная схема регулятора с использованием типовых звеньев САУ, выбрал параметры математической модели, исследовал схемы и определил схему с наилучшим регулированием. Во второй части курсовой работы: построил заданный код для передаваемого сообщения, произвел расчет корректирующих способностей кода, произвел структурный синтез кодирующего и декодирующего устройств, осуществил исследование корректирующих способностей синтезированного декодера при введении заданных искаженных кодовых комбинаций. Список литературы Видеоматериал / «Курсовая работа ТОАТ» -[https://www.youtube.com/watch?v=b2iSBsGbb5M&list=PL4o0lDYvp22_O3iHsQsmgrf3wO43GWlwd] Комогорцев М. Г. , Емельянов А. Г. Теоретические основы автоматики и телемеханики: Методические указания по выполнению курсовой работы – «Телекоммуникационные системы и сети на железнодорожном транспорте». – 2-е. стер. Чита: ЗабИЖТ, 2016. – 41 с. Сапожников В. В. Теоретические основы железнодорожной автоматики и телемеханики: учеб. для вузов / В. В. Сапожников [и др.]; под ред. В. В. Сапожникова. М.: Транспорт, 1995. 326 с. Тутевич В. Н. Телемеханика: учеб. для вузов. М.: Высш. шк., 1985. 423 с. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
