Нейросети. Добрица 4. Задача Провести обучение однослойной нейронной сети для указанной функции по правилу Розенблатта. 4 Логическая функция стрелка Пирса
 Скачать 51.16 Kb. Скачать 51.16 Kb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «Курский государственный университет» Кафедра программного обеспечения и администрирования информационных систем Направление подготовки «Математическое обеспечение и администрирование информационных систем» Форма обучения – очная Отчёт о выполнении лабораторной работы № 4 «Обучение нейронных сетей по правило Розенблатта и с помощью псевдообратных матриц» Дисциплина «Основы теории нейронных сетей»
Курск, 2020 Цель работы: освоить методы обучения нейронных сетей по правилу Розенблатта в полярном и биполярном случаях, а также с помощью псевдообратных матриц. Задача № 1. Провести обучение однослойной нейронной сети для указанной функции по правилу Розенблатта.
Задача № 2. Провести обучение однослойной нейронной сети для указанных данных в виде таблицы с помощью псевдообратных матриц для линейной функции активации.
Выполнение работы Задача 1. Логическая функция «стрелка Пирса»:
Обозначим начальные значения переменных 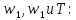 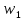 (0) = 0 (0) = 0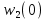 = 0 = 0T(0) = 0 α=0,5 Итерация 1.
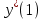 = sign( = sign(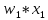 + + 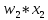 – T(0)) = sign(0*(–1) + 0*(–1) – 0) = –1 – T(0)) = sign(0*(–1) + 0*(–1) – 0) = –1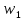 (1) = (1) = 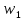 (0) + α (0) + α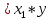 = 0 + 0,5*(–1)*1 = -0,5 = 0 + 0,5*(–1)*1 = -0,5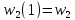 (0) + α (0) + α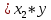 = 0 + 0,5*(–1)*1 = -0,5 = 0 + 0,5*(–1)*1 = -0,5T(1) = T(0+1) = T(0) - α* 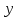 = 0 - 0,5*1 = -0,5 = 0 - 0,5*1 = -0,5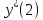 = sign( = sign(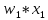 + + 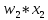 – T) = sign(-0,5 *(–1) + -0,5*1 + 0,5) = 1 – T) = sign(-0,5 *(–1) + -0,5*1 + 0,5) = 1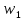 (1) = (1) = 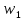 (0) + α (0) + α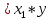 = -0,5 + 0,5*(–1)*(-1) = 0 = -0,5 + 0,5*(–1)*(-1) = 0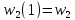 (0) + α (0) + α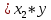 = -0,5 + 0,5*(–1)*1 = -1 = -0,5 + 0,5*(–1)*1 = -1T(1) = T(0+1) = T(0) - α* 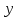 = -0,5 - 0,5*-1 = 0 = -0,5 - 0,5*-1 = 0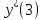 = sign( = sign(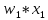 + + 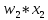 – T) = sign(-0*1 + -1*(–1) + 0) = 1 – T) = sign(-0*1 + -1*(–1) + 0) = 1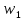 (1) = (1) = 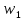 (0) + α (0) + α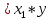 = 0 + 0,5*1*(-1) =-0,5 = 0 + 0,5*1*(-1) =-0,5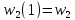 (0) + α (0) + α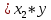 = -1 + 0,5*(–1)*(-1) = -0,5 = -1 + 0,5*(–1)*(-1) = -0,5T(1) = T(0+1) = T(0) - α* 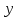 = 0 - 0,5*-1 = 0,5 = 0 - 0,5*-1 = 0,5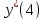 = sign( = sign(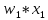 + + 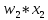 – T) = sign(-0,5 *1 + -0,5 * 1 - 0,5) = –1 – T) = sign(-0,5 *1 + -0,5 * 1 - 0,5) = –1Итерация 2.
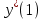 = sign( = sign(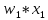 + + 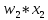 – T) = sign(-0,5*(–1) + -0,5*(–1) – 0,5) = 1 – T) = sign(-0,5*(–1) + -0,5*(–1) – 0,5) = 1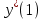 = sign( = sign(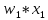 + + 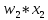 – T) = sign(-0,5*(–1) + -0,5*(1) – 0,5) = -1 – T) = sign(-0,5*(–1) + -0,5*(1) – 0,5) = -1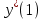 = sign( = sign(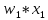 + + 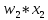 – T) = sign(-0,5*(1) + -0,5*(–1) – 0,5) = -1 – T) = sign(-0,5*(1) + -0,5*(–1) – 0,5) = -1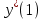 = sign( = sign(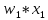 + + 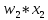 – T) = sign(-0,5*(1) + -0,5*(1) – 0,5) = -1 – T) = sign(-0,5*(1) + -0,5*(1) – 0,5) = -1Стабилизация достигнута, следовательно y = sign( 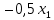  0,5 0,5 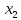  0,5) 0,5)Проверка: 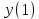 = sign( = sign(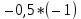  0,5 0,5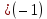  0,5) = 1 0,5) = 1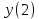 = sign( = sign(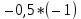  0,5 0,5 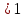  0,5) = 0,5) =  1 1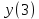 = sign( = sign(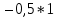  0,5 0,5 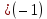  0,5) = 0,5) = 1 1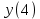 = sign( = sign(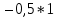  0,5 0,5 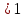  0,5) = 0,5) =  1 1Задача 2.
X = 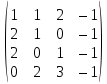 – матрица входных значений – матрица входных значенийY = 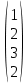 – матрица выходных значений – матрица выходных значенийY = X * W W = 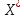 * Y * Y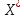 = = 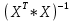 * * 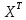 – псевдообратная матрица для матрицы X – псевдообратная матрица для матрицы XНайдём 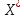 : :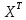 = =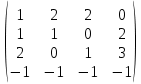 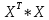 = = 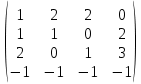 * * 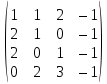 = = 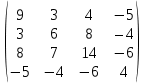 Найдем определитель получившейся матрицы 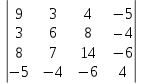 = =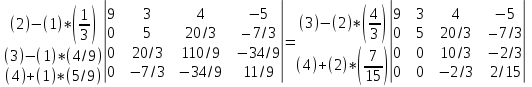 = = 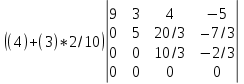 =0 =0Определитель данной матрицы равен 0, следовательно нельзя построить обратную матрицу |

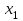
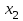
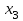
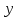
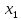
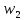
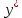
 –1
–1