РГЗ по радиофизике. Задача Условие Определить,если, a const. В декартовой системе координат построить силовые линии Решение
 Скачать 70.34 Kb. Скачать 70.34 Kb.
|
|
Министерство образования и науки РФ Новосибирский государственный технический университет РПиРПО РГР по радиофизике «Основы общей теории электромагнитного поля» Факультет: РЭФ Группа: РКС10-92 Студент: Келлерман Ф.Е. Преподаватель: Шадрина Г. С. Новосибирск 2011 1. Задача № 8. Условие: Определить 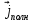 ,если ,если 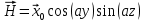 , a – const. В декартовой системе координат построить силовые линии , a – const. В декартовой системе координат построить силовые линии 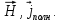 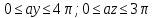 Решение: Для решения этой задачи используем первое уравнение Максвелла (уравнение полного тока). 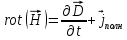 Т. к. в условии задачи не оговаривается значение вектора плотности тока смещения ( 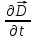 ), то можно принять его равным нулю. Тогда: ), то можно принять его равным нулю. Тогда: 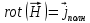 . . 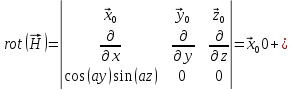 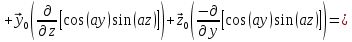 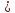 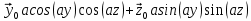 Построим силовые линии 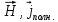 : :2. Задача № 20 Условие: По медному цилиндрическому проводнику ( R = 0.5 cm, σ = 5.7 107 сим/м) протекает постоянный ток, создающий перпендикулярный боковой поверхности вектор плотности потока мощности П = 10 Вт/м2(скалярное значение). Определить ток в проводнике и поток мощности через боковую поверхность ( на длине равной 1 м), пояснить рисунком. Решение: Электрический ток, протекающий через сечение проводника, определяется выражением: 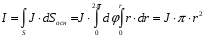 (1) (1)Согласно закону Ома в дифференциальной форме: 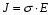 (2) (2)Подставим выражение (2) в (1) и выразим Е: 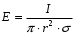 (3) (3)Запишем второе уравнение Максвелла в интегральной форме для кругового сечения проводника: 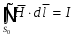 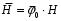 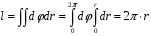 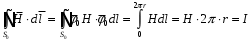 Откуда: 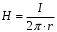 (4) (4)Плотность потока электромагнитной энергии равна векторному произведению напряженностей электрического и магнитного полей:  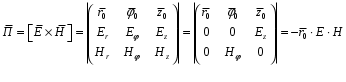 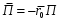 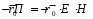 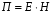 (5) (5)Подставим выражения (3) и (4) в выражение (5): 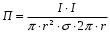 Откуда: 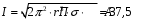  Поток мощности через боковую поверхность цилиндра: 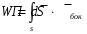 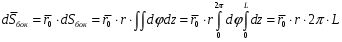  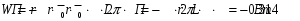 Найти выражение для потока энергии, проходящего через прямоугольный участок плоскости z = 2, имеющий реальные размеры по x от 0 до a, а по y от 0 до b, если векторы поля имеют вид: 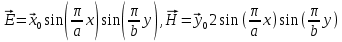 . .Построить графики П=П(х) при y = 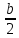 , П=П(y) при y = , П=П(y) при y = 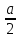 . .Решение: 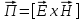 - вектор Пойтинга – плотность потока мощности. - вектор Пойтинга – плотность потока мощности. 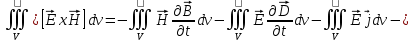 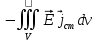 По теорема Остроградского – Гаусса: 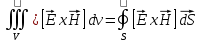 Где 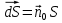 , , 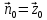 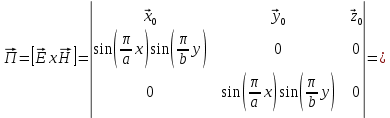 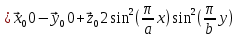 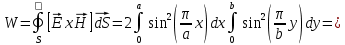 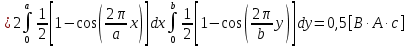 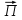 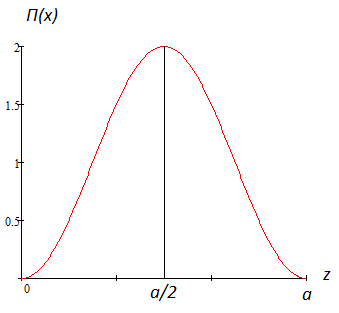 = =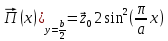 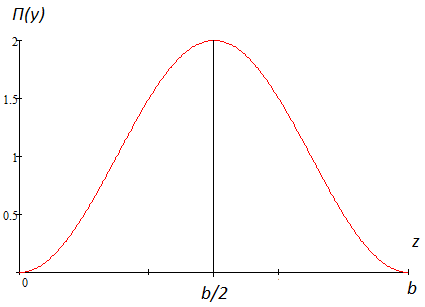 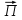 = =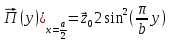 |
