физика к.р. Задача 1 ( 5) Условие задачи
 Скачать 185.8 Kb. Скачать 185.8 Kb.
|
|
Задача № 1 ( № 5) Условие задачи: При стрельбе из мелкокалиберной винтовки пуля, выпущенная в горизонтальном направлении с начальной скоростью 350 м/с, попадает на расстоянии 30 м. в точку прицеливания. Насколько ниже точки прицеливания будет попадать пуля при стрельбе на 100 м.?  Дано: Решение. Дано: Решение.Vср. = 350 м/с x = V0 × t × cosα (1)  ℓ = 100 м y = V0 × t × sinα – g ℓ = 100 м y = V0 × t × sinα – g 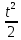 (2) (2)Через время t пуля преодолеет расстояние x = V0 × t × cosα. h=? Из уравнения: x = V0 × t × cosα вычисляем время t = 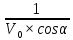 t = 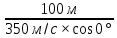 = 0,29 сек. = 0,29 сек.h = 100 м/с × sin 0 ° × 0,29 сек. - 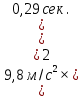 = == 0,42 м. Ответ: h= 0,42 м. Задача № 2( № 15) Условие задачи: Барабан сушильной машины диаметром D = 1,96 м. вращается с угловой скоростью ω = 20 рад/с. Определить во сколько раз сила F, с которой ткань прижимается к стенке, больше ее силы тяжести. Ответ записать целым числом. g = 9,8 м/с2  Дано: Решение. Дано: Решение.D = 1,96 м. m a = F’ = F g = 9,8 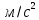 a = 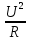 , U = ωR , U = ωRω = 20 рад/с  a = a = 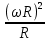 = = 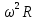 Fтяж. = ? U = 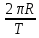 , U = ωR , U = ωRF = ? ω = 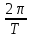 , F = mω2R, F = mg , F = mω2R, F = mg Составим чертёж: Составим чертёж:       R F F’’  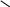 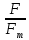 = = 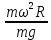 = = 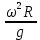 = = 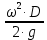 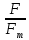 = =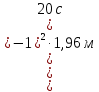 = = 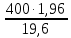 = 40 = 40Ответ: В 40 раз больше Задача № 3( № 25) Условие задачи: Маховик насажен на горизонтальный вал, который может легко вращаться в подшипниках. На цилиндрическую поверхность маховика радиусом 40 см. намотали гибкую нить, к свободному концу которой подвешена гиря массой 0,5 кг., и отпустили. Гиря начала опускаться, приводя маховик во вращение, и за 4 с. прошла 2 м. Найти момент инерции маховика.  Дано: Решение. Дано: Решение.R = 40 см = J = 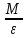 , M = TR , M = TR40 см / 100 = |T’| = |T| - по третьему закону Ньютона на ось y: 0, 40 м m = 0,5 кг S = 2 м mg – T = ma t = 4 c T = m ( g – a),  M = m( g-a) R M = m( g-a) RJ = ? ar = 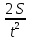 , ,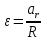 = =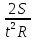 M = m (g - 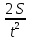 ) R ) RJ = 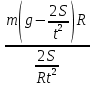 = = 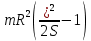 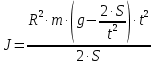 = = 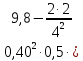 ) · ) · 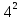 = =  = =  Ответ:  Задача № 4 ( № 35) Условие задачи: Материальная точка массой 0,1 кг. совершает гармонические колебания, уравнение которых имеет вид: x= 0,2sin8  Найти значение возвращающей силы в момент t = 0,1 с, а также полную энергию точки.  Дано: Дано:A= 0,2 w= 8*π m= 0,1 кг  t =1c t =1cE=? V=? Решение: x = 0,2· sin (8 × π × t), откуда: A = 0,2 и w = 8 × π v = dx/dt = 1,6 × π × cos ( 8 × π × t) a = - 0 2×( 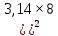 = 126,2 = 126,2 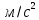 a (0,1) = - 162,2 sin 0,8 × π = -129,76 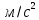 Найдём полную энергию: E = 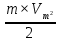 = 0,1 = 0,1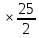 = 1,25 Дж = 1,25 ДжV = w 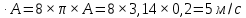 Ответ: E = 1,25 Дж, V= 5 м/с Задача № 5(№45) Условие задачи: До какой температуры охладятся 1,5 кг. воды с начальной температурой 1000 °С, если при этом выделяется 504 кДж тепла? Ответ дать в градусах Цельсия, выразив целым числом. Табличные данные: удельная теплоемкость воды сВ = 4,2 кДж/(кг*К)  Дано: Дано:m = 1,5 кг t = 1000 ° C С т = 504 кДж С воды = 4,2 кДж = 4200 Дж ( кг × °С)  Δt = ? Решение: Зная, что 1кДж = 1000 Дж находим: 504 кДж = 504 × 1000 = 504000 Удельная теплоёмкость вещества – это справочная величина. По справочным материалам определяем, что: С воды = 4,2 кДж = 4200 Дж ( кг × °С) Вычислим изменение температуры: Δt = 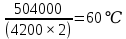 Ответ: Вода охладится на температуру 60 °С Задача № 6 ( № 55) Условие задачи: Кислород при неизменном давлении, равном 8*104 Па, нагревается. Его объем увеличивается от 1 м3 до 3 м3. Определить изменение внутренней энергии кислорода, работу, совершаемую им при расширении, а также количество теплоты, сообщенное газу. 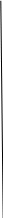 Дано: Дано:p = 8 · 10 4 Па = = 80 кПа V1 = 1 м3 V2 = 3 м3 p = const  ΔU =? A = ? Q = ? Решение: Первое начало термодинамики: Q = ΔU + A dA= pDV A = p ΔV = p ( V2 – V1) A= 8 · 10 4 · ( 3 – 1) = 1,6 · 10 4 Дж = 160 кДж Кислород – двухатомный газ, у его молекулы число степеней свободы: i = 5 ΔU = 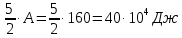 Согласно первому закону термодинамики количеств получаемой газом теплоты: Q = ΔU + A = 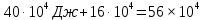 Дж ДжОтвет: A = 160 кДж = 16 · 104 Дж ΔU = 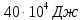 Q = 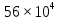 Дж ДжЗадача № 7 ( № 65) Условие задачи: Рассчитать для кислорода отношение удельной теплоемкости при постоянном давлении к удельной теплоемкости при постоянном объеме. Найти удельную теплоемкость кислорода: при постоянном давлении; при постоянном объеме.  Дано: Дано: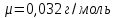 j = 5  Ср/ Сv = ? Решение: Отношение удельных теплоемкостей при постоянном давлении и постоянном объеме идеального газа равно отношению его молярных теплоемкостей при постоянном давлении и постоянном объеме: 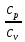 = =  Зная, что молярные теплоемкости при постоянном давлении и при постоянном объеме связаны с числом степеней свободы и равны  и и  = =  ·R ·RУ идеального двухатомного газа молярная теплоёмкость при постоянном давлении:  = =  = 3,5 = 3,5У идеального двухатомного газа молярная теплоёмкость при постоянном объёме: Cv =  · R = · R =  Остаётся поделить молярную теплоёмкость при постоянном давлении на молярную теплоёмкость при постоянном обьёме: 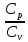 = = 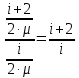 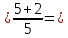 1,4 1,4Ответ: Ср = 3,5 Сv = 2,5 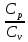 = 1,4 = 1,4Задача № 8 ( № 75) Условие задачи: К бесконечной, равномерно заряженной вертикальной плоскости подвешен на нити одноименно заряженный шарик массой m = 50 мг. и зарядом Q = 0,6 нКл. Сила натяжения нити, на которой висит шарик, F = 0,7 мН. Найти поверхностную плотность заряда на плоскости.  Дано: m = 50 мг = 5 · 10-5 Q = 0,6 нКл = 6 · 10 -10 F = 0,7 мН = 7 · 10 - 4   ? ?Справочные величины:   g = 9,8  Решение: Сделаем чертёж:  Здесь Т — сила натяжения нити, mg — сила тяжести, F — сила Кулона. Сумма проекций сил на ось OY: Tcosa-mg=0. Отсюда mg=T*cosacosa=mg/F=9,8*50*10-6/0,7*10-3 = 0,7 Отсюда угол a=45,57 град S ina = 0.71 Сумма проекций на ось ОХ: F-Tsina = 0 F=T*sina=0,7*10-3*0,71=0,5*10-3 H Напряженность электрического поля равна: E =  = =  отсюда поверхностная плотность заряда равна:  = = = 14,75 × = 14,75 ×   Ответ:  Задача № 9 ( № 85) Условие задачи: Плоский конденсатор состоит из двух круглых пластин радиусом 20 см. каждая. Расстояние между пластинами 5 мм. Конденсатор присоединен к источнику напряжения 3000 В. Определить заряд и напряженность поля конденсатора, если диэлектриком будут: 1) воздух; 2) стекло.  Дано: Дано:R=20 см = 0,2 м d=5мм  U = 3000 В        Решение: Известно, что ёмкость плоского конденсатора  , ,где  диэлектрическая проницаемость диэлектрика( в нашем случае диэлектрическая проницаемость диэлектрика( в нашем случае  , , ), ),d – расстояние между пластинами, S – площадь пластин.  электрическая постоянная. электрическая постоянная.Так как пластины круглые, то их площадь равна  , ,Поэтому С = 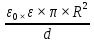 С другой стороны известно, что С = 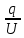 , где q – заряд на пластинах, U – приложенное напряжение. Поэтому q= U × C = , где q – заряд на пластинах, U – приложенное напряжение. Поэтому q= U × C = 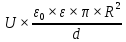 , ,откуда для 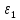 =1 имеем =1 имеем 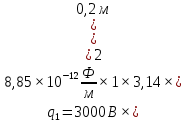 = == 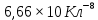 = 66,6 нКл = 66,6 нКлДля 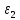 имеем: имеем: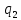 = = 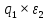 = =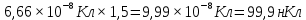 Напряжённость по определению, равно: 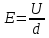 , ,Оно будет постоянно при любой среде между обкладками , если поддерживается постоянная разность потенциала U, поэтому: 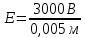 = = 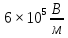 Ответ: 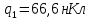 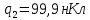 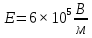 Задача № 10 ( №95) Условие задачи: В схеме на рисунке 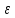 - генератор с Э.Д.С., равной 120 В, R3 = 20 Ом, R4 = 25 Ом и падение напряжения на R1 равно 40 В. Амперметр показывает 2 А. Найти сопротивление R2. Сопротивлением генератора и амперметра пренебречь. - генератор с Э.Д.С., равной 120 В, R3 = 20 Ом, R4 = 25 Ом и падение напряжения на R1 равно 40 В. Амперметр показывает 2 А. Найти сопротивление R2. Сопротивлением генератора и амперметра пренебречь.  Дано: Дано:E = 120 В 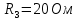 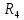 = = 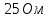 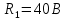 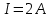  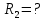 Решение: Исходя из приведённого чертежа установки:  Из закона Ома найдём сопротивление   , где сопротивление цепи , где сопротивление цепиR =  ; ;Сопротивление R2 :  = =  = = Ответ:  Задача № 11 ( № 105) Условие задачи: Две электролитические ванны с растворами AgNO3 и CuSO4 соединены последовательно. Какая масса m2 меди выделится за время, в течении которого выделилась m1 = 180 мг. серебра?  Дано: Дано: = 180 мг = = 180 мг == 180 ×   = 1 = 1   Решение: Для электрического тока справедливы два закона Фарадея 1 закон Фарадея: Масса вещества выделявшегося при электролизе. m =  , ,где q – количество электричества, прошедшего через электролит, K – электролитический эквивалент, 2 закон Фарадея:  , ,где A – молярная масса, z – валентность, F – 96,48456 ×  – постоянная Фарадея. – постоянная Фарадея.Тогда для серебра:  = =  × ×  = 1,12 × = 1,12 ×  Для меди: 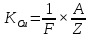 = = 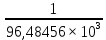 × × 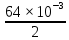 = = 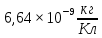 Отсюда, произведение времени на ток:  Тогда масса меди равна:   = 6,64 × = 6,64 ×  × × = 10,67 × = 10,67 ×  Ответ:  10,67 × 10,67 ×  Задача № 12 ( № 115) Условие задачи: Электрон в невозбужденном атоме водорода движется (согласно теории Бора), вокруг ядра по окружности радиусом 0,529× 10 -8 см. Движение электрона по окружности эквивалентно круговому току. Определить магнитный момент атома водорода, обусловленный этим круговым током.  Дано: Дано: =0,529 =0,529  =   B=? U = ? S = ? I = ?   Решение: Магнитный момент  по определению это произведение силы кругового тока I на обтекаемую им площадь делённое на скорость света S: по определению это произведение силы кругового тока I на обтекаемую им площадь делённое на скорость света S:  ( в системе СГС). В системе СИ на скорость света не делят . Поэтому ( в системе СГС). В системе СИ на скорость света не делят . Поэтому  В нашем случае I =  , где e- заряд электрона, а V- его скорость на первой , где e- заряд электрона, а V- его скорость на первойорбите  Площадь S = Площадь S =  где r – радиус первой где r – радиус первой боровской орбиты атома водорода. Тогда получаем  = =  3,606152273= 3,606152273= Ответ: Магнитный момент  Задача № 13 (№ 125) Условие задачи: Электрон движется в однородном магнитном поле перпендикулярно линиям индукции. Определить силу F, действующую на электрон со стороны поля,если индукция поля В = 0,2 Тл, а радиус кривизны траектории R = 0,2 см. Дано:  B = 0,2 Тл = 0,002 B = 0,2 Тл = 0,002r = 0,2 см e =    Найти силу F Решение: Формула силы Лоренца: F = qBU, где q = e(заряд электрона), B - индукция магнитного поля, U - скорость электрона. Приравниваем силу Лоренца к центробежной силе и получаем следующее уравнение:  = eBU -> (U сокращаются) -> = eBU -> (U сокращаются) ->  = eB; = eB; Единственное что нам не известно, это скорость U. Выведем её из уравнения: U =  ; ; Теперь подставим скорость в формулу силы Лоренца: F =  ; ; Заряд и масса электрона это известные константы, так что осталось только вычислить: F =  Ответ: F =  Задача № 14( № 135) Условие задачи: На дифракционную решетку падает свет длиной волны 760 нм. При этом для спектра 3-го порядка получается угол отклонения 10011'. Определить постоянную дифракционной решетки.  Дано: Дано: = 760 нм = 760 нм = 3 = 3 = 10011’ = 10011’ d = ? Решение: Будем считать, что заданные углы отклонению соответствуют максимумам при дифракции света на решётке. Из условия максимумов для дифракционной решётки с постоянной d имеем:  = =  Из уравнения получаем: d =  Находим: d =  = =  = =  |
