Теория сигналов и систем. РГР 86 вариант. Задача 1 3 Задача 2 12 Задача 3 22 Задача 4 26 Заключение 29 Список использованных источников 31
 Скачать 242.95 Kb. Скачать 242.95 Kb.
|
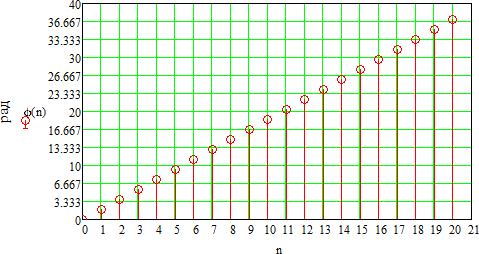 Рисунок 1.4 – Фазовая спектральная диаграмма сигнала с периодом T1 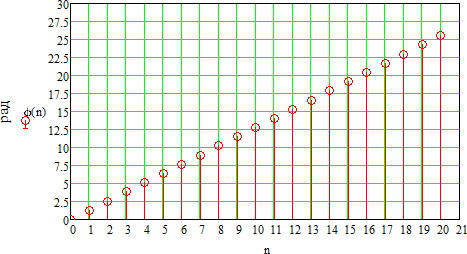 Рисунок 1.5 – Фазовая спектральная диаграмма сигнала с периодом T2 Задача 2 Определить спектральную плотность униполярного прямоугольного импульса, изображенного на рис. 6. Построить АЧХ и ФЧХ спектральной плотности при заданных длительности и амплитуде импульса. С использованием полученных графиков построить аналогичные зависимости для импульсов вдвое меньшей длительности. Отобразить на графиках влияние задержки импульса на время 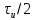 . Сравнить спектры импульсной последовательности из задачи 1 и одиночного импульса. . Сравнить спектры импульсной последовательности из задачи 1 и одиночного импульса.Длительность импульса и его величина из задачи 1. 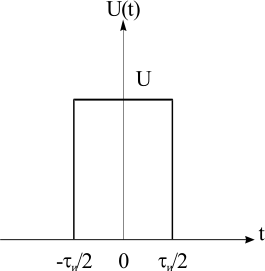 Рисунок 2.1 - Одиночный прямоугольный видеоимпульс Исходные данные: 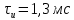 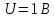 Решение: Найдем спектральную плотность прямоугольного видеоимпульса, применив к нему преобразование Фурье: 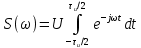 Применив формулу Эйлера: 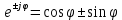 Получим: 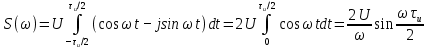 Для последующего упрощения умножим и разделим правую часть на 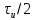 и упростим: и упростим: 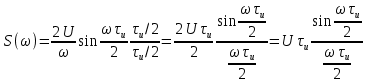 График симметричен относительно вертикальной оси, вычислим первые 20 положительных точек графика. Таблица 2.1 - Спектралная плостность импульса с большой длительностью
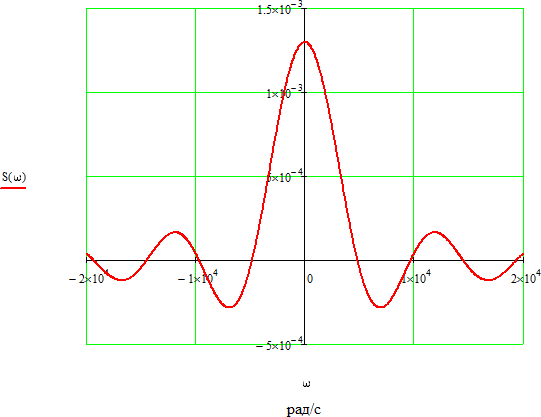 Рисунок 2.2 - Спектральная плотность сигнала Значение спектральной плотности на нулевой частоте равно площади импульса: 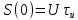 Найдем частоты перехода S(w) через ноль. 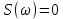 при при 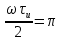 , тогда: , тогда: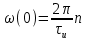 Где n-целое число. Найдем значения данных частот для первых трех лепестков графика: 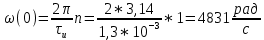 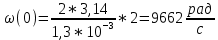 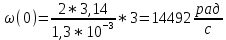 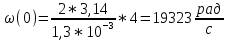 Так как спектральная плотность есть комплекснозначная функция частоты, то она имеет действительную и мнимую части: 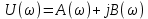 Где 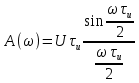 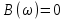 В нашем случае для спектральной плотности прямоугольного видеоимпульса мнимая часть равна нулю. Тогда модуль спектральной плотности будет описываться формулой: 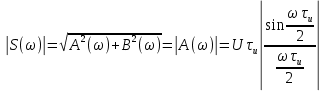 Построим график Таблица 2.2 - АЧХ спектральной плотности импульса с большой длительностью
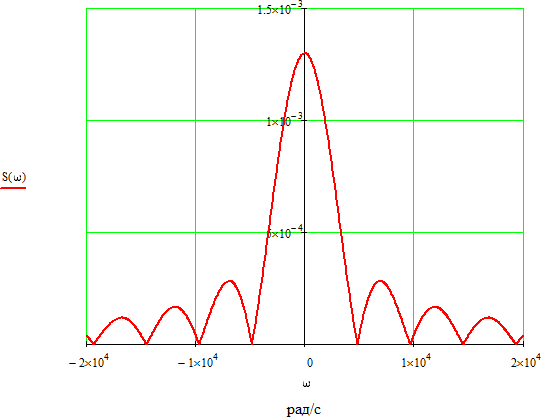 Рисунок 2.3 - АЧХ спектральной плотности сигнала Фазовый спектр прямоугольного видеоимпульса определяется по формуле: 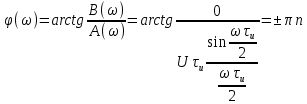 Где 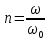 , , 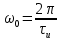 . .Фаза импульса изменяется скачком в точках, где значение спектральной плотности проходит через нуль. Таблица 2.3 - ФЧХ спектральной плотности импульса с большой длительностью
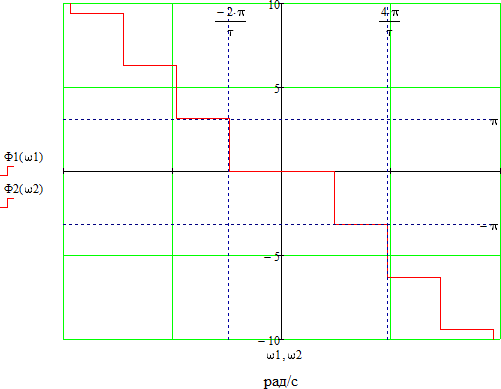 Рисунок 2.4 - ФЧХ спектральной плотности сигнала Построим аналогичные графики для случая, когда импульсы вдвое меньшей длительности 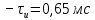 . .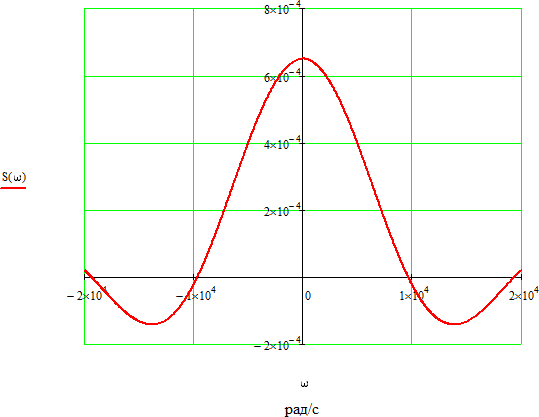 Рисунок 2.5 - Спектральная плотность сигнала 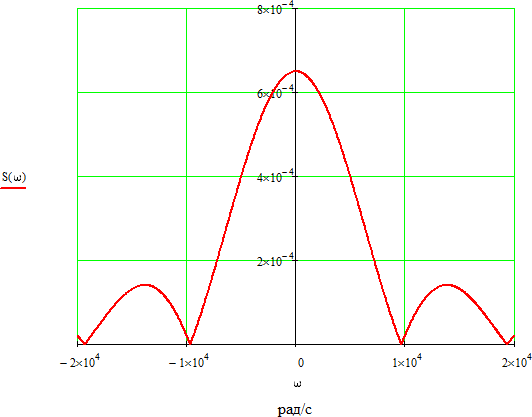 Рисунок 2.6 - АЧХ спектральной плотности сигнала 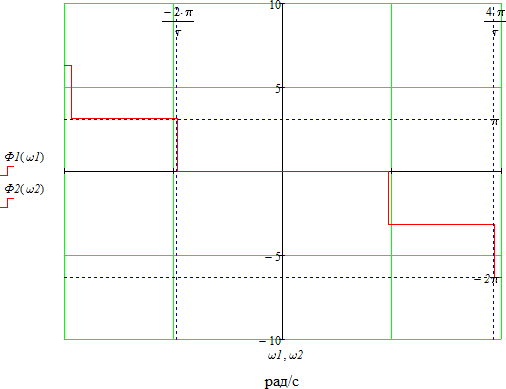 Рисунок 2.7 - ФЧХ спектральной плотности сигнала При уменьшении длительности импульса в 2 раза полоса частот, занимаемая его спектром, также расширяется в 2 раза при относительном уменьшении амплитуд гармонических составляющих. Найдем спектральную плотность в случае задержки импульса на τu/2 по формуле: 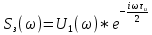 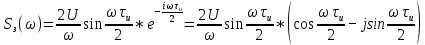 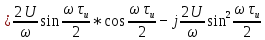 или 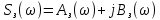 , где , где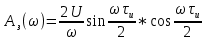 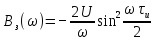 Найдем АЧХ и ФЧХ полученной спектральной плотности: 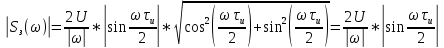 Из этого следует, что АЧХ при задержке на τu/2 не изменяется. 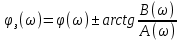 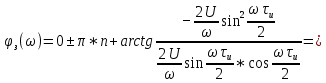 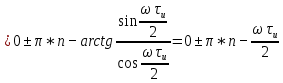 Таблица 2.5 - ФЧХ спектральной плотности сигнала с длительностью импульса 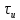
Таблица 2.6 - ФЧХ спектральной плотности сигнала с длительностью импульса 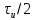
Построим ФЧХ спектральной плостности для сигналов с длительностями импульсов, равными 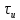 и и 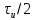 . .1 - ФЧХ спектральной плотности сигнала с длительностью импульса |
