Задача 1. a Найти наибольшее значение функции f 504x 1 75x 2 при следующих ограничениях
 Скачать 27 Kb. Скачать 27 Kb.
|
|
Практическая задача №1. a) Найти наибольшее значение функции F = 504x1 + 75x2 при следующих ограничениях: 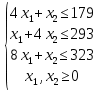 b) Используем графический метод решения. Рассмотрим неравенство 1 системы ограничений. 4 x1 + x2 ≤ 179 Построим прямую: 4 x1 + x2 = 179 Пусть x1 =0 => x2 = 179 Пусть x2 =0 => 4 x1 = 179 => x1 = 179/4 Найдены координаты двух точек (0, 179) и (179/4 ,0). Соединяем их и получаем необходимую прямую (1). Рассмотрим неравенство 2 системы ограничений. x1 + 4 x2 ≤ 293 Построим прямую: x1 + 4 x2 = 293 Пусть x1 =0 => 4 x2 = 293 => x2 = 293/4 Пусть x2 =0 => x1 = 293 Найдены координаты двух точек (0, 293/4) и (293 ,0). Соединяем их и получаем необходимую прямую (2). Рассмотрим неравенство 3 системы ограничений. 8 x1 + x2 ≤ 323 Построим прямую: 8 x1 + x2 = 323 Пусть x1 =0 => x2 = 323 Пусть x2 =0 => 8 x1 = 323 => x1 = 323/8 Найдены координаты двух точек (0, 323) и (323/8 ,0). Соединяем их и получаем необходимую прямую (3). Строим область допустимых решений: 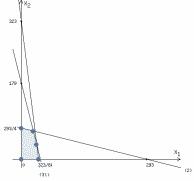 Строим вектор C = (504, 75), координатами которого являются коэффициенты функции F. Функция F достигает наибольшего значения в точке A. 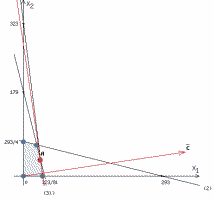 Точка A одновременно принадлежит прямым (1) и (3). 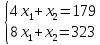 => => 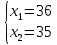 Вычислим значение функции F в точке A (36,35). F (A) = 504 * 36 + 75 * 35 = 20769. Ответ: 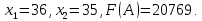 c) Составим двойственную задачу к исходной. Количество переменных в двойственной задаче равно количеству неравенств в исходной. Матрица коэффициентов двойственной задачи является транспонированной к матрице коэффициентов исходной. Система ограничений двойственной задачи записывается в виде неравенств противоположного смысла неравенствам системы ограничений прямой задачи. Если исходная задача на максимум, то двойственная будет на минимум. Получаем следующую двойственную задачу: 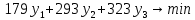 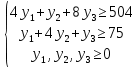 Из теоремы двойственности: 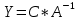 . .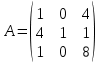 , , 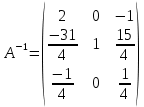 . .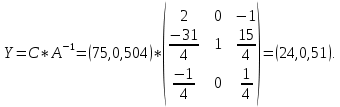 Оптимальный план двойственной задачи равен: 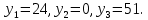 179*24+293*0+323*51 = 20769. Экономическая интерпретация:
| |||||||||||||||||||||||||
