ТипЗадачиПРиА(проект). Задача 1 Аппарат диаметром d 2 м и высотой l 5 м покрыт слоем асбеста толщиной 75 мм. Температура стенки аппарата t
 Скачать 79.96 Kb. Скачать 79.96 Kb.
|
|
Типовые задачи по дисциплине "Процессы и аппараты биотехнологии (проект)" Задача 1 Аппарат диаметром D = 2 м и высотой L = 5 м покрыт слоем асбеста толщиной δ = 75 мм. Температура стенки аппарата tг = 146ºС, а наружной поверхности асбеста tх = 40ºС. Определить потери теплоты (тепловой поток) через слой изоляции. Принять для асбеста λ = 0,151 Вт/(м·К). Решение: Потери теплоты (тепловой поток) через слой изоляции (асбеста) происходят путем теплопроводности 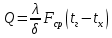 . .Поверхность теплообмена 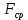 включает площадь дна и крышки аппарата, которые без изоляции, а так же боковую поверхность аппарата, покрытую асбестом. Следовательно, для расчета поверхности дна и крышки используют диаметр аппарата D, а для определения боковой поверхности применяют средний диаметр (аппарат + асбест), который составляет включает площадь дна и крышки аппарата, которые без изоляции, а так же боковую поверхность аппарата, покрытую асбестом. Следовательно, для расчета поверхности дна и крышки используют диаметр аппарата D, а для определения боковой поверхности применяют средний диаметр (аппарат + асбест), который составляет  . Значит поверхность теплообмена . Значит поверхность теплообмена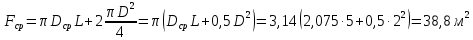 , ,А согласно формуле (1) потери теплоты равны: 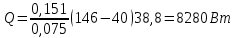 . .Ответ: 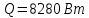 Задача 2 Стенка аппарата состоит из двух слоев толщиной δ1= 500 и δ2= 250 мм. Температура внутри аппарата t1= 1300ºС, а наружного воздуха t5= 25ºС. Определить потери теплоты с 1 м2 поверхности стенки и на границе слоев (t3). Принять, Вт/(м2·К): α1=34,8 и α2=16,2. Коэффициенты теплопроводности слоев, Вт/(м·К): λ1=1,16 и λ2=0,58. Решение: Потери теплоты с 1 м2 (тепловой поток) рассчитываются по формуле: 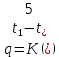 , (1) , (1)для которой коэффициент теплопередачи определяют из выражения 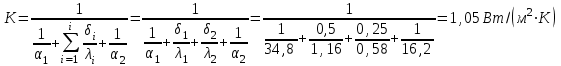 Следовательно, потери тепла с 1 м2, согласно формуле (1), составят: Следовательно, потери тепла с 1 м2, согласно формуле (1), составят: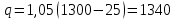 Вт/м2 Вт/м2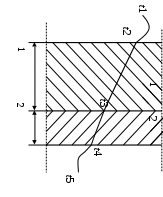 Рис. 1 Температура на границе слоёв находится из теплового баланса (поток тепла к стенке равен потоку через первый слой изоляции) согласно рис. 1 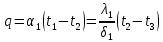 , (2) , (2)причем температуру t2 вычисляем по формуле температуры стенки 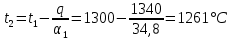 . .Теперь искомую температуру на границе слоёв можно найти из формулы (2) 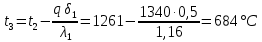 . .Ответ: 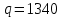 Вт/м2 и Вт/м2 и 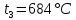 Задача 3 Начальная и конечная температуры горячего теплоносителя (1) составляют 300ºС и 200ºС, а холодного (2) теплоносителя 25ºС и 175ºС. Определить среднюю разность температур при движении теплоносителей прямотоком. Решение:  Для прямотока начальные температуры теплоносителей на одном конце аппарата, а конечные на другом: 300 200 Для прямотока начальные температуры теплоносителей на одном конце аппарата, а конечные на другом: 300 200 25 175 25 175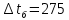  . .Отношение разностей температур на концах теплообменника: 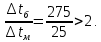 Следовательно, для нахождения средней разности температур при данном прямотоке надо применять логарифмическую формулу  . .Ответ: 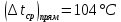 . .Задача 4 Определить среднюю разность температур в теплообменнике со смешанным током теплоносителей, если начальная и конечная температура горячего теплоносителя t1н = 80 и t1к = 40ºС, а холодного теплоносителя t2н = 10 и t2к = 34ºС. Решение: Средняя разность температур для смешанного тока теплоносителей определяется по средней разности температур противотока 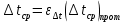 . (1) . (1)Множитель 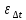 является функцией числовых коэффициентов P и R , то есть является функцией числовых коэффициентов P и R , то есть 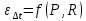 и находится из справочных таблиц. Числовые коэффициенты определяются по формулам: и находится из справочных таблиц. Числовые коэффициенты определяются по формулам: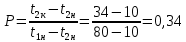 , ,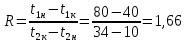 . .По этим значениям числовых коэффициентов из справочника находят 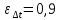 . . Величину Величину 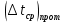 находят из схемы: 80 40 находят из схемы: 80 40 34 10 34 10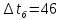 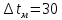 Отношение разностей температур на концах теплообменника: 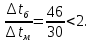 Следовательно, для нахождения средней разности температур при данном противотоке можно применить формулу среднего арифметического: 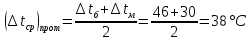 . .Средняя разность температур для смешанного тока по формуле (1): 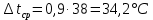 . .Ответ: 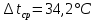 . .Задача 5 В аппарате требуется охладить жидкость от температуры t2H =90 ºС до температуры t2K =50 ºС Массовый расход жидкости G2 =9000 кг/ч с теплоёмкостью с2=2900 Дж/кг. Начальная температура охлаждающей воды t1н =18ºС, а конечная t1к =40ºС. Коэффициент теплопередачи К =270 Вт/(м2∙К). Определить необходимую поверхность теплообмена при прямотоке и противотоке. Решение: Из основного уравнения теплопередачи тепловая нагрузка аппарата составляет: 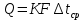 , ,а, значит необходимая поверхность теплообмена 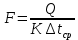 . (1) . (1)Тепловую нагрузку определяет как количество тепла, отдаваемое жидкостью  . .Среднюю разность температур определяем отдельно для прямотока и противотока.  Для прямотока: 90 50 Для прямотока: 90 50 18 40 18 40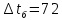 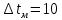 . .Значит, средняя разность температур определяется по формуле: 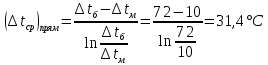 . . Для противотока: 90 50 Для противотока: 90 50 40 18 40 18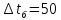 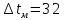 Отношение разностей температур на концах теплообменника:  Следовательно, для нахождения средней разности температур при данном противотоке можно применить формулу среднего арифметического: 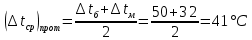 . .Тогда поверхность теплообмена при прямотоке согласно формуле (1) составит  , ,а для противотока: 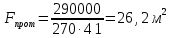 . .Ответ: 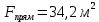 и и 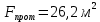 |
