теория вероятности. 8060811_Теор_вер. Задача 5 3 Задачи 15 4 Задачи 25 6 Задачи 35 7 Задачи 45 10 Задачи 55 11 Задачи 65 12 Задачи 75 д 13
 Скачать 50.91 Kb. Скачать 50.91 Kb.
|
|
Оглавление Задача № 5 3 Задачи № 15 4 Задачи № 25 6 Задачи № 35 7 Задачи № 45 10 Задачи № 55 11 Задачи № 65 12 Задачи № 75 Д 13 Задача № 5Отдел по управлению персоналом фирмы проводит опрос для выяснения мнений работников по определенной программе обучения. Известно, что среди n = 28 работников фирмы k = 8 прошли обучение по интересующей фирму программе и с вероятностью p = 0,8 могут дать ей квалифицированную оценку. Фирма случайным образом отбирает четырех работников из общего числа работников. Чему равна вероятность того, что в ходе опроса будет получена квалифицированная оценка программы обучения? Событие А - в ходе опроса будет получена квалифицированная оценка Гипотезы: Н0 - из отобранных четырех человек ни одного, прошедшего обучение Н1 - из отобранных четырех человек один, прошедший обучение Н2 - из отобранных четырех человек два, прошедших обучение Н3 - из отобранных четырех человек три, прошедший обучение Н4 - из отобранных четырех все 4 прошли обучение 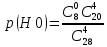 = 1*4845/20475 = 0,237 = 1*4845/20475 = 0,237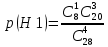 = 8*1140/20475 = 0,445 = 8*1140/20475 = 0,445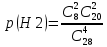 = 28*190/20475 = 0,26 = 28*190/20475 = 0,26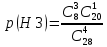 = 56*20/20475 = 0,055 = 56*20/20475 = 0,055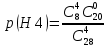 = 70*1/20475 = 0,003 = 70*1/20475 = 0,003Для каждой из гипотез вероятность квалифицированной оценки по формуле произведения вероятностей: p(A|H0) = 0 p(A|H1) = 1-0,2 = 0,8 p(A|H2) = 1-0,2^2 = 0,96 p(A|H3) = 1-0,2^3 = 0,992 p(A|H3) = 1-0,2^4 = 0,9984 Тогда, искомая вероятность p(A) = 0,237*0+0,445*0,8+0,26*0,96+0,055*0,992+0,003*0,99984 = 0,663 Задачи № 15Из общего числа кандидатов, участвующих в конкурсе на вакантную должность руководителя, 25 % по итогам комплексной оценки не удовлетворяют профилю минимальных требований. Случайно выбраны n = 4 кандидата. Построить ряд распределения для случайной величины X - числа кандидатов в выборке, не удовлетворяющих профилю минимальных требований. Найти функцию распределения, математическое ожидание и среднее квадратическое отклонение случайной величины X. Используя функцию распределения, определить вероятность того, что число кандидатов, не удовлетворяющих профилю минимальных требований, будет от 2 до 4. Данные о значениях i и n взять из таблицы 2. Перечислим все возможные значения случайной величины Х: 0, 1, 2, 3, 4. Вероятность того, что каждый из отобранных не удовлетворяют профилю минимальных требований, - постоянна и равна 0,25 (p = 0,25). Вероятность противоположного события, т.е. того, что каждый из отобранных удовлетворяют профилю минимальных требований 0,75 (q = 1 - p = 1 - 0,25 = 0,75). Все 4 испытания – независимы. Очевидно, что случайная величина Х - подчиняется биномиальному закону распределения вероятностей с параметрами n=4 и p=0,25. Итак, по условию задачи: n = 4; p = 0,25; q = 0,75; X = m. Расчет искомых вероятностей осуществляется по формуле Бернулли. 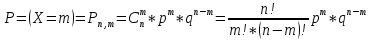 Подставим в эту формулу данные задачи: P(X=0) = 1*0,25^0*0,75^4 = 0,316 P(X=1) = 4*0,25^1*0,75^3 = 0,422 P(X=2) = 6*0,25^2*0,75^2 = 0,211 P(X=3) = 4*0,25^3*0,75^1 = 0,047 P(X=3) = 1*0,25^4*0,75^0 = 0,004 Получим ряд распределения числа кандидатов в выборке, не удовлетворяющих профилю минимальных требований:
Так как все возможные значения случайной величины образуют полную группу событий, то сумма их вероятностей должна быть равна 1. Функция распределения F(X). F(x≤0) = 0 F(0< x ≤1) = 0.316 F(1< x ≤2) = 0.422 + 0.316 = 0.738 F(2< x ≤3) = 0.211 + 0.738 = 0.949 F(3< x ≤4) = 0.047 + 0.949 = 0.996 F(x>4) = 1 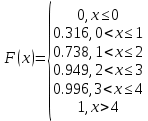 Математическое ожидание находим по формуле m = ∑xipi. Математическое ожидание M[X]. M[x] = 0*0.316 + 1*0.422 + 2*0.211 + 3*0.047 + 4*0.04 = 1.145 Дисперсию находим по формуле d = ∑x2ipi - M[x]2. Дисперсия D[X]. D[X] = 02*0.316 + 12*0.422 + 22*0.211 + 32*0.047 + 42*0.04 - 1.1452 = 1.018 Среднее квадратическое отклонение σ(x). Вероятность попадания СВ в тот ли иной интервал находится по формуле: P(a ≤ X < b) = F(b) - F(a) Найдем вероятность того, что СВ будет находиться в интервале 2 ≤ X < 4 P(2 ≤ X < 4) = F(4) - F(2) = 0.996 - 0.738 = 0.258 Задачи № 25Зависимость производительности труда от величины материального стимулирования (доплаты, премии, льготы и др.) в течение года описывается следующей функцией плотности распределения вероятностей 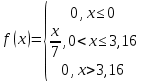 Необходимо найти функцию распределения F(x), математическое ожидание M(X) и дисперсию D(X). Чему равна вероятность того, что производительность составит меньше двух единиц? Функция распределения. F(x) = 1, x > 3.16 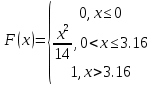 Математическое ожидание. = Дисперсия. = = Среднеквадратическое отклонение. Вероятность того, что производительность составит меньше двух единиц P(x<2) =  = 4/14 = 0,286 = 4/14 = 0,286Задачи № 35При изучении итогов тестирования N претендентов на вакантную должность секретаря по схеме собственно-случайной выборки в кадровом агентстве было отобрано 100 претендентов. Полученные данные представлены в группированном виде интервалами количества баллов xi, набранных в результате тестирования, и количеством ni претендентов, попавших в i - ый интервал:
Для анализа распределения претендентов по количеству набранных баллов необходимо: 1) дать графическое изображение ряда в виде гистограммы относительных частот; 2) найти эмпирическую функцию распределения и построить ее график; 3) найти несмещенные и состоятельные оценки среднего количества набранных баллов и дисперсии среднего количества набранных баллов для претендентов на данную вакантную должность по всем кадровым агентствам города; 4) сделать предварительный выбор закона распределения, обосновав свой выбор Таблица для расчета показателей.
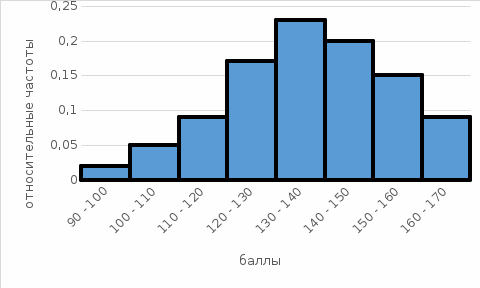 Рис. 1 Гистограмма относительных частот Эмпирическая функция распределения F(X). F(x≤90) = 0 F(90 F(100 F(110 F(120 F(130 F(140 F(150 F(160 F(x>170) = 1 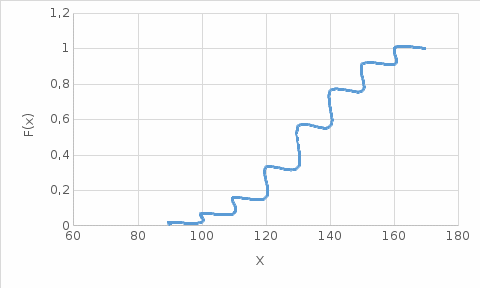 Рис. 2 Функция распределения Для оценки ряда распределения найдем следующие показатели: Показатели центра распределения. Средняя взвешенная (выборочная средняя) Несмещенная оценка дисперсии - состоятельная оценка дисперсии (исправленная дисперсия). = Оценка среднеквадратического отклонения. Распределение близко к нормальному - все значения ряда попадают в интервал 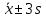 Задачи № 45Для данных своего варианта к задачам №31-40 определить, предполагая, что количество набранных баллов распределено нормально: 1) вероятность того, что количество набранных претендентами баллов по всем кадровым агентствам отличается от средних выборочных не более, чем на Δ = 2 баллов (по абсолютной величине); 2) границы, в которых с вероятностью 0,99 заключено среднее количество набранных баллов для претендентов на данную вакантную должность по всем кадровым агентствам города; 3) долю претендентов, имеющих 140 набранных баллов и выше, гарантируя результат с вероятностью 0.95. Вероятность того, что абсолютная величина |X-a| отклонения окажется меньше δ. Вероятность того, что отклонение нормально распределенной случайной величины от ее математического ожидания по абсолютной величине не превзойдет некоторого положительного числа δ, то есть |X- a| < δ, определяется так: Доверительный интервал для генерального среднего. Поскольку n>30, то определяем значение tkp по таблицам функции Лапласа. В этом случае 2Ф(tkp) = γ Ф(tkp) = γ/2 = 0.99/2 = 0.495 По таблице функции Лапласа найдем, при каком tkp значение Ф(tkp) = 0.495 tkp(γ) = (0.495) = 2.58 (136.9 - 4.396;136.9 + 4.396) = (132.5;141.3) С вероятностью 0.99 можно утверждать, что среднее значение при выборке большего объема не выйдет за пределы найденного интервала. Интервальное оценивание генеральной доли (вероятности события). Всего претендентов, имеющих 140 баллов и выше = 67 – их доля = 0,67 Доверительный интервал для генеральной доли. (p* - ε ; p* + ε) Поскольку n>30, то определяем значение tkp по таблицам функции Лапласа. В этом случае 2Ф(tkp) = γ Ф(tkp) = γ/2 = 0.95/2 = 0.475 По таблице функции Лапласа найдем, при каком tkp значение Ф(tkp) = 0.475 tkp(γ) = (0.475) = 1.96 (0.67-0.0922; 0.67+0.0922) (0.578; 0.762) или в %: (57.784; 76.216) С вероятностью 0.95 при большем объеме выборки, эта доля будет находиться в заданном интервале. Задачи № 55По данным своего варианта к задачам №31-40 при уровне значимости α =0,1 проверить гипотезу о том, что среднее количество набранных баллов для претендентов на данную вакантную должность по всем кадровым агентствам города равно 137,9 баллов. Выдвигается нулевая гипотеза H0 о том, что значение математического ожидания генеральной совокупности равно числу μ0: = 137.9 Альтернативная гипотеза: H1: μ ≠ 137.9, критическая область – двусторонняя. Для проверки нулевой гипотезы используется случайная величина: где x – выборочное среднее; S – среднеквадратическое отклонение генеральной совокупности. Если нулевая гипотеза верна, то случайная величина T имеет стандартное нормальное распределение. Критическое значение статистики T определяется исходя из вида альтернативной гипотезы: P(|T| < tкр) = 1 - α, Ф(tкр)=(1-α)/2 Найдем экспериментальное значение статистики T: Поскольку объем выборки достаточно большой (n>30), то вместо истинного значения среднеквадратического отклонения можно использовать его оценку S=17.038. Ф(tкр)=(1-α)/2 = (1-0.1)/2 = 0.45 По таблице функции Лапласа найдем, при каком tkp значение Ф(tkp) = 0.45 tkp = 1.65 (-∞ ;-1.65)U(1.65; +∞) Экспериментальное значение критерия T не попало в критическую область T < tkp, поэтому нулевую гипотезу следует принять. Значение математического ожидания генеральной совокупности можно принять равным 137.9. Задачи № 65По данным своего варианта к задачам №31-40, учитывая, что аналогичное обследование, проведенное год назад, показало, что среднее квадратическое отклонение количества набранных претендентами баллов равно S = 18.038 баллов, проверить есть ли основание считать одинаковыми отклонения от среднего количества набранных претендентами баллов в данном периоде и в соответствующем периоде предыдущего года. Проверку осуществить при уровне значимости α = 0.05 и предположении, что количество набранных претендентами баллов распределено нормально. При уровне значимости α = 0,05 проверить гипотезу Н0 о равенстве дисперсий двух нормально распределенных случайных величин Х и Y на основе выборочных данных при альтернативной гипотезе: H1 σ1^2 ≠ σ2^2 . Дисперсии σ1^2 = 290,293 σ2^2 = 325,37 Вычислим наблюдаемое значение критерия F = σ2^2/ σ1^2 = 325,37/290,293 = 1,12 Найдем критическое значение при уровне значимости 0,05/2 = 0,025 и числам степеней свободы k1 = m −1 = 99, k2 = n −1 = 99 Fкрит = 1,394 Так как Fнабл < Fкрит, нет оснований отвергнуть нулевую гипотезу. Задачи № 75 ДДля эмпирического распределения количества набранных претендентами при тестировании баллов по данным своего варианта к задачам №31-40 подобрать соответствующее теоретическое распределение и на уровне значимости α проверить гипотезу о согласованности двух распределений с помощью критерия χ2 - Пирсона. Проверим гипотезу о том, что Х распределено по нормальному закону с помощью критерия согласия Пирсона. где pi - вероятность попадания в i-й интервал случайной величины, распределенной по гипотетическому закону Для вычисления вероятностей pi применим формулу и таблицу функции Лапласа где s = 17.039, xср = 136.9 Теоретическая (ожидаемая) частота равна ni = npi, где n = 100 Вероятность попадания в i-й интервал: pi = Ф(x2) - Ф(x1)
Определим границу критической области. Так как статистика Пирсона измеряет разницу между эмпирическим и теоретическим распределениями, то чем больше ее наблюдаемое значение Kнабл, тем сильнее довод против основной гипотезы. Поэтому критическая область для этой статистики всегда правосторонняя: [Kkp;+∞). Её границу Kkp = χ2(k-r-1;α) находим по таблицам распределения χ2 и заданным значениям s, k (число интервалов), r=2 (параметры xcp и s оценены по выборке). Kkp = χ2(8-2-1;0.01) = 15.08627; Kнабл = 2.49 Наблюдаемое значение статистики Пирсона не попадает в критическую область: Кнабл < Kkp, поэтому нет оснований отвергать основную гипотезу. Справедливо предположение о том, что данные выборки имеют нормальное распределение. 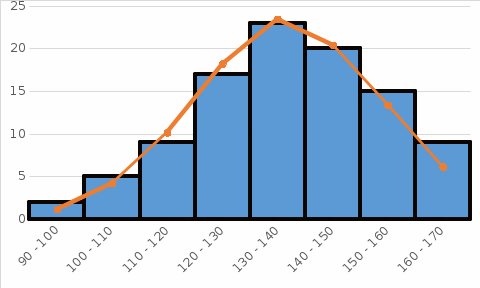 Рис. 2 Гистограмма и кривая теоретического нормального распределения. |
