Парная линейная регрессия. 2. 3 Парная линейная регрессия
 Скачать 50.71 Kb. Скачать 50.71 Kb.
|
2.3 Парная линейная регрессия2.3.1 Вопросы для обсуждения: Что такое функция регрессии? Чем регрессионная модель отличается от функции регрессии? Назовите основные причины наличия в регрессионной модели случайного отклонения. Назовите основные этапы регрессионного анализа. Что понимается под спецификацией модели, и как она осуществляется? В чем состоит различие между теоретическим и эмпирическим уравнениями регрессии? Дайте определение теоретической линейной регрессионной модели. В чем суть метода наименьших квадратов (МНК)? Приведите формулы расчета коэффициентов эмпирического парного линейного уравнения регрессии по МНК. Как связаны эмпирические коэффициенты линейной регрессии с выборочным коэффициентом корреляции между переменными уравнения регрессии? Какие выводы можно сделать об оценках коэффициентов регрессии и случайного отклонения, полученных по МНК? 2.3.2 Пример решения задач. Для анализа зависимости объема потребления Y (у.е.) домохозяйства от располагаемого дохода X(у.е.) отобрана выборка объема n = 12 (помесячно в течение года), результаты которой приведены в таблице 2. Необходимо определить вид зависимости; по МНК оценить параметры уравнения регрессии Y на X; оценить силу линейной зависимости между Xи Y; спрогнозировать потребление при доходе X= 160. Таблица 2 – Зависимость объема потребления домохозяйства от располагаемого дохода
Для определения вида зависимости построим корреляционное поле (рисунок 3). 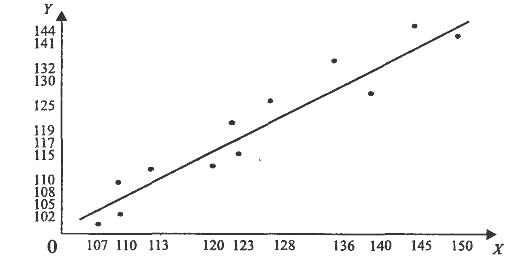 Рисунок 3 – Поле корреляции По расположению точек на корреляционном поде полагаем, что зависимость между X и Y линейная: Y =b0 + b1Х. Для наглядности вычислений по МНК построим таблицу 3. Согласно МНК, имеем 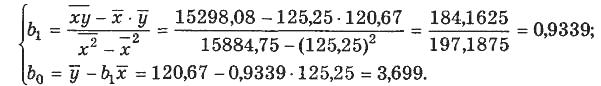 Таким образом, уравнение парной линейной регрессии имеет вид: Ŷ = 3,699 + 0.9339Х. Изобразим данную прямую регрессии на корреляционном поле. По этому уравнению рассчитаем ŷi, а также ei = yi- ŷi Для анализа силы линейной зависимости вычислим коэффициент корреляции: 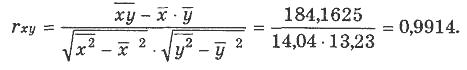 Данное значение коэффициента корреляции позволяет сделать вывод о сильной (прямой) линейной зависимости между рассматриваемыми переменными X и Y. Это также подтверждается расположением точек на корреляционном поле. Таблица 3 – Расчет параметров уравнения регрессии по МНК
Прогнозируемое потребление при располагаемом доходе х по данной модели составит ŷ(160) = 153,12. Построенное уравнение регрессии требует определенной интерпретации и анализа. Интерпретация требует словесного описания полученных результатов с трактовкой найденных коэффициентов, с тем чтобы построенная зависимость стала понятной человеку, не являющемуся специалистом в эконометрическом анализе. В нашем примере коэффициент b1может трактоваться как предельная склонность к потреблению (МРС = 0,9339). Фактически он показывает, на какую величину изменится объем потребления, если располагаемый доход возрастает на одну единицу. На графике (рисунок 3) коэффициент b1определяет тангенс угла наклона прямой регрессии относительно положительного направления оси абсцисс (объясняющей переменной). Поэтому часто он называется угловым коэффициентом. Свободный член b0уравнения регрессии определяет прогнозируемое значение Yпри величине располагаемого дохода X, равной нулю (т.е. автономное потребление). Однако здесь необходима определенная осторожность. Очень важно, насколько далеко данные наблюдений за объясняющей переменной отстоят от оси ординат (зависимой переменной), так как даже при удачном подборе уравнения регрессии для интервала наблюдений нет гарантии, что оно останется таковым и вдали от выборки. В нашем случае значение b0 = 3,699 говорит о том, что при нулевом располагаемом доходе расходы на потребление составят в среднем 3,699 у.е. Этот факт можно объяснить для отдельного домохозяйства (оно может тратить накопленные или одолженные средства), но для совокупности домохозяйств он теряет смысл. В любом случае значение коэффициента b0определяет точку пересечения прямой регрессии с осью ординат и характеризует сдвиг линии регрессии вдоль оси Y. 2.3.3 Задачи и упражнения для самостоялельного решения 1) В следующей выборке представлены данные по цене Р некоторого блага и количеству (Q) данного блага, приобретаемому домохозяйством ежемесячно в течение года.
а) Постройте корреляционное поле и по его виду определите формулу зависимости между Р и Q. б) Оцените по МНК параметры уравнения линейной регрессии. в) Оцените выборочный коэффициент корреляции rpq. г) Проинтерпретируйте результаты. 2) Дана таблица недельного дохода (X) и недельного потребления (Y) для 60 домашних хозяйств. а) Для каждого уровня дохода рассчитайте среднее потребление, являющееся оценкой условного математического ожидания б) Постройте корреляционное поле для данной выборки. в) Постройте эмпирическое линейное уравнение регрессии, используя все данные. г) Постройте эмпирическое линейное уравнение регрессии, используя только средние значения потребления для каждого уровня дохода. д) Сравните построенные уравнения. Какое из них, с вашей точки зрения, ближе к теоретическому? е) Рассчитайте выборочный коэффициент корреляции для в) и г). Будет ли линейная связь между данными переменными существенной? Обоснуйте ответ. Таблица 4 – Доходы и расходы на потребление домашних хозяйств
3) По выборке объема п = 10 получены следующие данные: ∑ xi = 993,4; ∑ уi = 531,3; ∑ xiyi= 53196,61; ∑xi2= 105004,5; rху= 0,75. Рассчитайте оценки коэффициентов регрессии Y на Xи Xна Y. 2.3.4 Литература: [5], [6], [10], [11], [18]. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
