ргз физика. Физика 21 вариант (1). Задача 1 Даны зависимости координат от времени х(t) t 2 y(t) 4 t
 Скачать 119.73 Kb. Скачать 119.73 Kb.
|
ЗАДАНИЯ ДЛЯ РАСЧЁТНО-ГРАФИЧЕСКИХ РАБОТ ЗАДАЧА №1Даны зависимости координат от времени. х(t)=t2; y(t)=4t2+2t;z(t)=0 а) Определите зависимости радиус-вектора частицы, скорости, ускорения от времени и найдите их модули. б) Найдите уравнение траектории, дайте оценку характера движения материальной точки вдоль траектории.    в) Постройте графические зависимости: у(х), υх(t), a(t). в) Постройте графические зависимости: у(х), υх(t), a(t).
    Частица движется равноускоренно. Найдём уравнение траектории Частица движется равноускоренно. Найдём уравнение траектории x t 2 t x t 2 t y 4t2 2t y 4х 2 Графические зависимости: 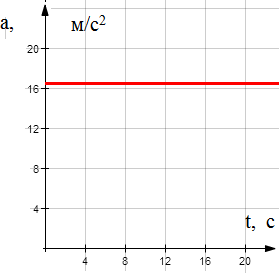   а) б) в) а) б) в)Рис. 1. а – зависимость ускорения от времени; б – зависимость проекции скорости на ось хот времени; в –зависимость координаты yот х. 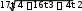  Ответ:r→ t2i→ 4t2 2t →j; r→ Ответ:r→ t2i→ 4t2 2t →j; r→ ; y 4х 2 ;   → 2ti→ 8t 2 →j; → 2ti→ 8t 2 →j; 68t2 32t 4; 8t; a→ 2i→ 8 →j; a→ 16, 5 м/ с2 х  частица движется вдоль траектории равноускоренно частица движется вдоль траектории равноускоренно Материальная точка движется по окружности радиусом R=8м. При заданном уравнении движения материальной точки S(t) = 0,5 + 4t + t2 определите: а) тангенциальное ускорение aτ,нормальное ускорение anи полное a ускорение в момент времени t1=2с; б) характер движения материальной точки. Постройте графические зависимости S(t), υ(t), a(t) Дано: Решение:V(t) S/ (t) 4 2t;V(2) 8 м S(t) =0,5 +4t+t2 t1=2сR=8м Найти:aτ=?an=?a=? Построить графики:S(t), υ(t), a(t) сТангенциальное ускорение a : a(t) S// (t) V/ (t) 2 м с2 V 1 Нормальноеускорениеan: 2 4 2t2 a(t) t2 2t 2; n R 8 2 a(2) 8 м n с2 Полноеускорение:   a(t) a(t)  a(2) 8, 25 м a(2) 8, 25 мс2 с2  Частица движется по окружности с ускорением a(t) Частица движется по окружности с ускорением a(t) Графические зависимости:   а) б) в) Рис. 2. а – зависимость S(t) ; б– зависимость V(t); в– зависимость a(t) Ответ:a 2 м; a 8 м; a 8, 25 м с2 n с2 с2 Из ямы глубиной h=1 м бросают тело под углом =600 к горизонту со скоростью υ0=8м/с. Тело вылетает из ямы. Найдите: 1) положение и скорость тела через время t1=1с;2) максимальные высоту и дальность полета; 3) уравнение траектории тела. Постройте графические зависимости S(t), υ(t), a(t) Дано: Решение: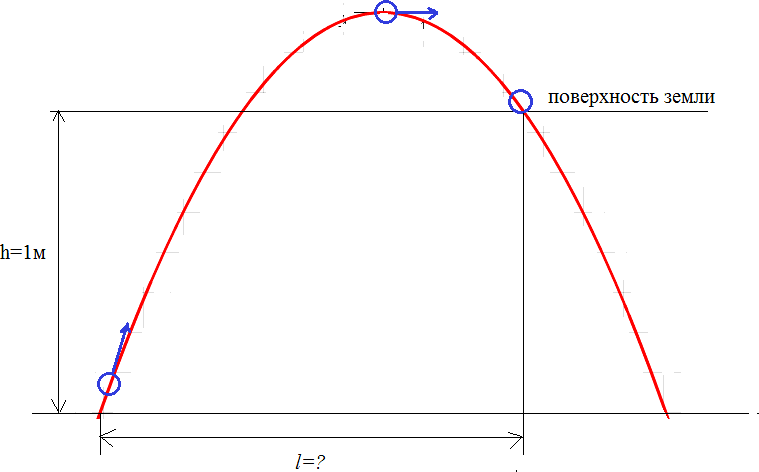 h=1 м h=1 м=600 υ0=8м/с t1=1сg=9,8м/с2Найти: x1=? у1=? V=? hmax=? l=?y(x)=? Построить:S(t), υ(t), a(t) Положение тела через время t1=1снайдем за формулами: x1 V0t1cos gt 2 y1 V0t1 sin 1 2 Подставляя числовые значения, получим: x 8 м1с 1 4м 1 с 2 9,8 м1с2 y 8 м1сsin 600 с2 1 с 2 2м Скорость тела через время t1=1сопределим за формулой:  V VПодставляя числовые значения, получим: V Максимальная высота поднятия: 4, 9 м 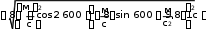 с с м2 3 2  2 2 8 с 2 2 2 8 с 2 hmax V0 sin 2g 2 9,8 м с2 2, 45м Дальность полета: V2 sin 2 м2 8 с sin1200 l0 5, 7 м g 9,8 м с2 Уравнение траектории тела: х x V0tcos 2 y Vtsin gt x 4t y 4 3t 5t2 t 4  х х2 х х2 0 2 y 4 5 4 4 y(х) 3х 5 х2 уравнение траектории тела( с учетом, что g 10 м) с2 Найдем зависимости S(t), υ(t), a(t) 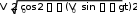   S(t) x(t) V0tcos 4t S(t) x(t) V0tcos 4tV(t)  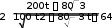 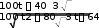 a(t) V/ (t) a(t) V/ (t) Графические зависимости: а) б) в)    Рис. 3. а – зависимость S(t) ; б– зависимость V(t); в– зависимость a(t) Груз массой m=3кгначинает двигаться из состояния покоя вдоль гладкой горизонтальной плоскости под действием силы F, причем Fх = t. Найдите зависимость x = f(t), (x(0) = 0). Постройте графические зависимости Fх=f(t), υх=f(t) и x=f(t). Дано: Решение: m=3кгFх=tx(0) = 0 m=3кгFх=tx(0) = 0V0=0 Найти:x= f(t) Построить:Fх=f(t) υх=f(t) x=f(t). Т at2 Ft2 t t2 t3 Тогда x(t) x (м) 2 2m 2 3 6 t3 / υх=x/ (t) 3t2 t2 м 6 Графические зависимости: 6 2 с    а) б) в) а) б) в)Рис. 4. а– зависимость Fх(t); б– зависимость υх(t); в–зависимость x(t) Ответ:x(t) at2 2 Два стальных шара массами m1=1 кг и m2=0,2 кг подвешены на нитях так, что при их касании центры находятся на ℓ=2 м ниже точек подвеса, а нити вертикальны. Меньший шар отводят в сторону (при этом нить отклоняется на угол =900) и отпускают. Принимая шары за абсолютно упругие, определите, на какую высоту поднимутся их центры шаров после удара. Что произойдет, если таким же образом отклонить большой шар? Постройте графическую зависимость h1= f(m1). Дано: Решение:m1=1 кг Потенциальная энергия меньшего шара до удара пойдет на m2=0,2 кг изменение потенциальной энергии шаров после удара ℓ=2 м m2gl=( m1+ m2)gh =900 Отсюда Найти:h Построить: h1= f(m1). m2 gl ( m1 m2 )gh h m2 gl m2l ( m1 m2 )g m1 m2 0, 2кг 2м0, 2кг 1кг 0, 33м Если таким же образом отклонить большой шар, то m1 gl ( m1 m2 )gh h m1 gl m1l 1кг 2м 1, 67 м ( m1 m2 )g m1 m2 0, 2кг 1кг Запишем зависимость h1= f(m1) hm 2m1 m 1 1 1 0, 2 Графическая зависимость Рис. 5. зависимость Рис. 5. зависимостьh1 m1 Ответ:0,33Человек стоит на неподвижной горизонтальной скамье Жуковского и ловит мяч массой m1=0,3кг, летящий в горизонтальном направлении на расстоянии ℓ=0,5м от оси вращения скамейки. После этого скамейка начала вращаться с угловой скоростью ω=1рад/с. Момент инерции человека и скамейки J=5кг м2. Определить скорость движения мяча относительно неподвижного наблюдателя. Дано: Решение: m1=0,3кг ℓ=0,5м ω=1рад/с J=5кг м2 Найти: m1=0,3кг ℓ=0,5м ω=1рад/с J=5кг м2 Найти:ЗАДАЧА №7 V Ответ: 33,8 м с Найти напряженность поля тяготения планеты в точках, расстояние которых от центра планеты равно 0R; 0,5R; 1,0R; 1,5R; 2,0R; 2,5R; 3,0R; 3,5R, 4R, где R=24622м – радиус планеты. Постройте графическую зависимость напряжённости поля тяготения планеты от расстояния r, считая, что плотность вещества планеты одинакова по всему объему и равна ρ=5430кг/м3, вне планеты плотность вещества близка к нулю. На какой высоте над поверхностью планеты напряженность её поля тяготения уменьшится в N=2 раза? Постройте графическую зависимость потенциала от расстояния r, в интервале 0<r<2Rгде 2R- два радиуса планеты. Дано: Решение:R=24622м N=2 G= 6, 67 10 11 м3 кг с2 Материальные точки притягиваются друг к другу с силами, пропорциональными произ- ведению их масс и обратно пропорциональ- ρ=5430кг/м3 Найти: Е(0R), Е(0,5R), Е(1R), Е(1,5R), Е(2R), Е(2,5R), Е(3R), Е(3,5R), Е(4R), h Построить: Е(r) φ(r) ными квадрату расстояния между ними: F G mM R2 Рассмотрим гравитационное поле, создавае- мое точечной массой М. Очевидно, что оно обладает сферической симметрией – вектор напряженности E в любой его точке направлен к массе М , создающей поле, и равен по вели- чине E F F GMm r2 M V 4 R3 3 4 R3G Подставляя числовые данные получим ТогдаE 3r2 E(r) Тогда 4 3,14 5430 кг 24622м3 м3 3r2 6, 67 10 11 м3 кг с2 2, 26 107 Н r2 м Е( 2, 26 107 Н 2, 26 107 Н 0R)= , Е(0,5R)= 0, 5 24622м2 0,15 м, Е(1R)= 1 24622м2 0, 0375 м, Е( 2, 26 107 2 Н 2, 26 107 3 Н 1,5R)= 1, 7 10 2 1, 5 24622м м, Е(2R)= 2 24622м2 9, 4 10 м, Е( 2, 26 107 3 Н 2, 26 107 3 Н 2,5R)= 6 10 2 2, 5 24622м м , Е(3R)= 3 24622м2 4 10 м, Е( 2, 26 107 3 Н 2, 26 107 3 Н 3,5R)= 310 2 3, 5 24622м м, Е(4R)= 4 24622м2 2, 310 м Найдем на какой высоте над поверхностью планеты напряженность её поля тяготения уменьшится в N=2 раза. 2, 26 107 E(R) E(R h) R2 2, 26 107 R h2 2, 26 107 N E(R) E(R h) 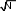 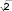 R h2 R2 NR h R R h2 R2 NR h RR2 2, 26 107 R h2 R h2 R2  h R h R R 24622м 24622м 10198м Графические зависимостиа) б)   Рис. 6. а – зависимость Е(r); б– зависимость φ(r) |
