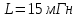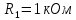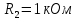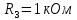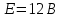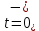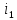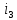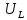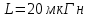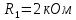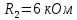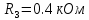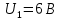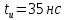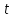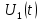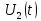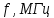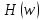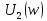РГР ТЭЦ. РГР ТЭЦ ЗС-021. Задача 1 Дано
 Скачать 192.05 Kb. Скачать 192.05 Kb.
|
|
Федеральное агентство связи Федеральное государственное бюджетное образовательное учреждение высшего образования Сибирский государственный университет телекоммуникаций и информатики СибГУТИ кафедра ТЭЦ Расчетно-графическая работа №2 Вариант 35 Выполнил: студентка гр. ЗС-021 Агуреева П.В. Новосибирск 2022 ЗАДАЧА 3.1
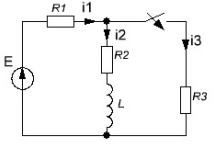 а рис.1 схема цепи: Рисунок 1 - Исходная схема Требуется: Рассчитать основные характеристики процесса; Получить выражения для токов i t 2 , i t 3 и напряжения u tL классическим методов; Построить графики указанных токов и напряжений; рассчитать ток i t 2 операторным методом. Р 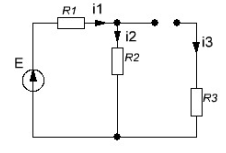 ешение: Рисунок 2 - Схема при t= 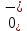 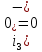 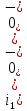 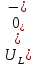 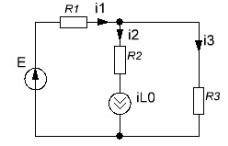 Рисунок 3 - Схема при t= 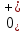 по закону коммутации 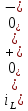 Составим систему по з. Кирхгофа 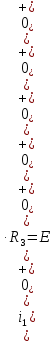 Решая систему получаем 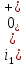 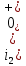 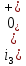 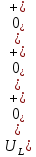 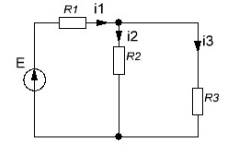 Рисунок 4 - Схема при 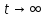 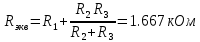 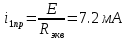 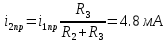 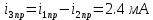 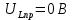 Для удобства сведем полученные значения в таблицу 2. Таблица 1 - Значения токов и напряжений при переходном процессе
Найдем корень характеристического уравнения 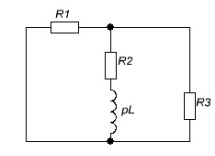 Рисунок 5 - Схема для нахождения корня характеристического уравнения 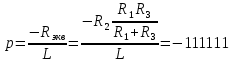 Аналитическое выражение для переходных процессов 1 порядка имеет общий вид 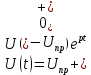 Подставим полученные значения в пункте 3 в эту формулу 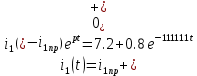 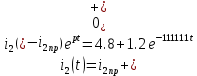 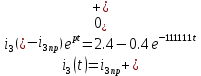 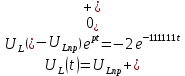 Определим длительность переходного процесса. Для этого найдем постоянную времени 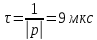 Длительность переходного процесса равна (3-5) 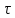 , следовательно , следовательно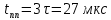 По полученным формулам в п.4 построим графики переходных токов и напряжения на катушке. 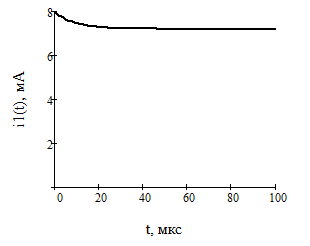 Рисунок 6 - Зависимость 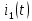 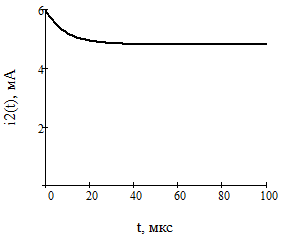 Рисунок 7 - Зависимость 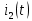 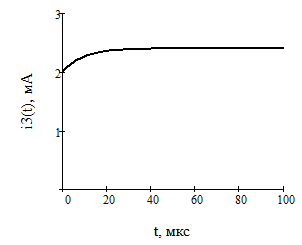 Рисунок 8 - Зависимость  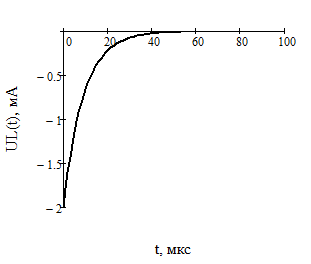 Рисунок 9 - Зависимость  Рассчитаем ток 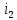 операторным методом. операторным методом.Найдем ННУ 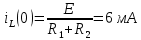 Составим операторную схему замещения для момента времени t= 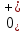 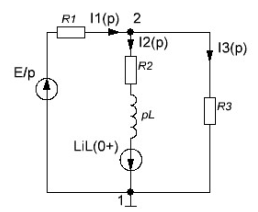 Рисунок 10 - Операторная схема замещения Составим уравнение по методу узловых потенциалов. Первый узел примем за базисный. 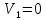 Тогда получаем 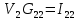 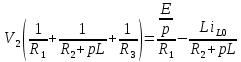 Выразим 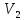 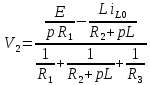 По з.Ома операторный ток 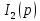 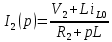 Подставим 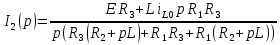 После числовых подстановок 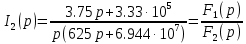 Найдем корень знаменателя 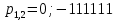 Тогда по формуле разложения оригинал тока имеет вид 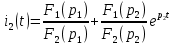 Найдем производную 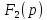 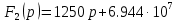 Подставим значения 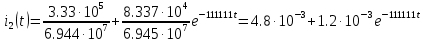 Как видим токи сошлись. ЗАДАЧА 3.2
На рис.11 схема цепи: 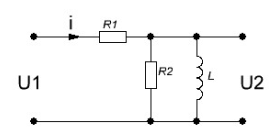 Рисунок 11 - Исходная схема Рассчитать переходную g t 2 и импульсную h t 2 характеристики цепи по напряжению классическим или операторным методами (по выбору). Рассчитать реакцию цепи в виде выходного напряжений u t2 используя: интеграл Дюамеля; интеграл наложения. Построить временные диаграммы входного и выходного напряжений. Решение: Переходной характеристикой цепи 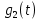 является реакция цепи на воздействие в виде единичной функции. Переходная характеристика имеет вид является реакция цепи на воздействие в виде единичной функции. Переходная характеристика имеет вид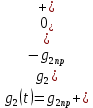 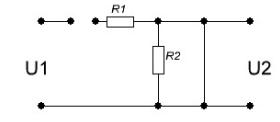 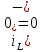 Рисунок 12 - Схема при t= 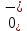 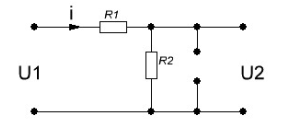 По закону коммутации 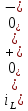 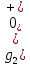 Рисунок 13 - Схема при t= 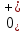 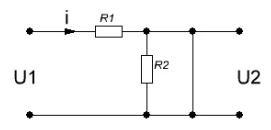 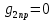 Рисунок 14 - Схема при 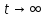 Найдем корень характеристического уравнения 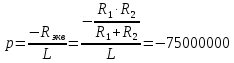 Таким образом, переходная характеристика примет вид 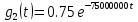 Импульсную характеристику цепи 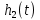 можно найти из переходной характеристики по формуле можно найти из переходной характеристики по формуле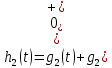 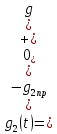 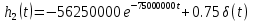 Найдем скачки и производные входного сигнала 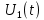 для участков. для участков.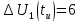 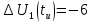 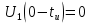 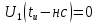 Запишем выражения для выходного сигнала 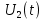 с помощью интеграла Дюамеля. с помощью интеграла Дюамеля.1 интервал 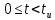 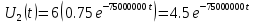 2 интервал 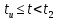 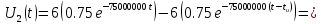 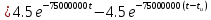 В отличие от интеграла Дюамеля в интеграле наложения не учитываются дополнительные слагаемые скачки входного напряжения 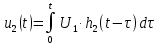 Подставляя полученные ранее значения Для интервала 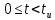 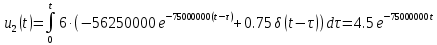 Для интервала 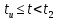 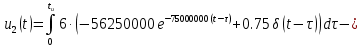 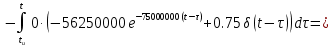 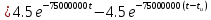 Рассчитаем выходной сигнал до момента времени 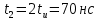 с помощью этих формул с шагом 7 нс и занесем полученные данные в таблицу 4. с помощью этих формул с шагом 7 нс и занесем полученные данные в таблицу 4.Все расчеты производились в среде Mathcad. Таблица 2 - Отсчеты входного и выходного сигнала
Построим получившийся график на рисунке 15. 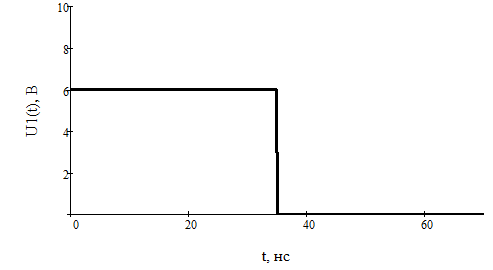 Рисунок 15 - Входной сигнал 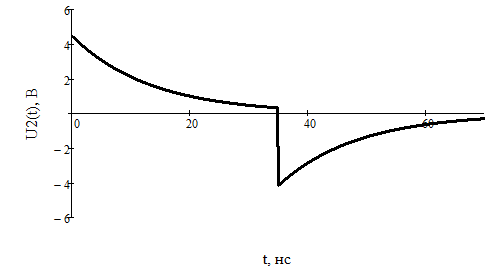 Рисунок 16 - Выходной сигнал Для расчета комплексной спектральной плотности непериодического сигнала 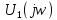 используется прямое преобразование Фурье. Для заданного входного сигнала преобразование Фурье принимает выражение используется прямое преобразование Фурье. Для заданного входного сигнала преобразование Фурье принимает выражение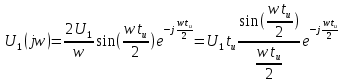 Комплексная спектральная плотность выходного сигнала 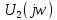 находится по формуле находится по формуле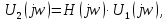 где  Функция 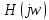 находится как отношение комплексного значения гармонического напряжения находится как отношение комплексного значения гармонического напряжения 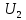 на выходе цепи к комплексному значения гармонического напряжения на выходе цепи к комплексному значения гармонического напряжения 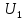 той же частоты, приложенному ко входу цепи: той же частоты, приложенному ко входу цепи: 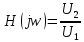 Для схемы приведенной на рисунке 11 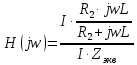 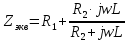 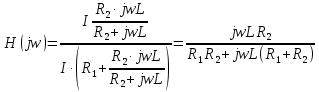 Амплитудно-частотная характеристика (АЧХ) этой цепи 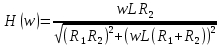 Модуль спектральной плотности входного сигнала 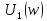 будет равен будет равен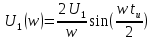 Для построения графиков полученных функций необходимо выбрать расчетные точки по частоте. Учтем, что спектральная плотность одиночного прямоугольного импульса обращается в ноль на частотах 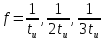 и т.д. Поэтому дополнительно выбираются промежуточные точки между этими частотами. Максимальная частота в соответствие с заданием равна и т.д. Поэтому дополнительно выбираются промежуточные точки между этими частотами. Максимальная частота в соответствие с заданием равна 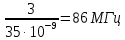 . Результаты расчетов сводим в таблицу 5. . Результаты расчетов сводим в таблицу 5.Таблица 3 - Модуль спектральной плотности и АЧХ цепи
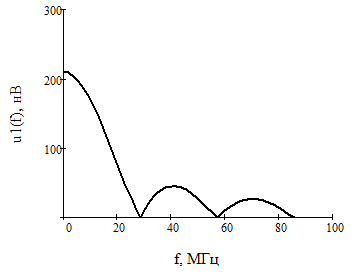 Рисунок 17 - Амплитудный спектр входного сигнала 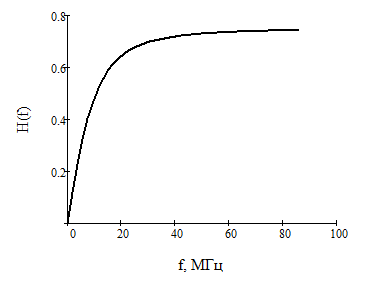 Рисунок 18 - АЧХ цепи 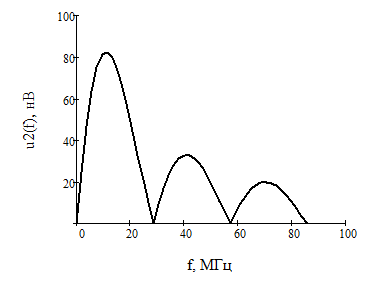 Рисунок 19 - Амплитудный спектр выходного сигнала |