контрольная работа по техмеху. Задача №1. Задача 1 i ii iii 2 0 1 Дано

• Название: Задача 1 i ii iii 2 0 1 Дано
• Анкор: контрольная работа по техмеху
• Дата: 22.01.2023
• Размер: 20.53 Kb.
• Имя файла: Задача №1.docx
• Тип: Задача; #898226

Задача №1

I	II	III
2	0	1

Дано: Вариант №

Схема 1 L= 4 м F₁= 40·10^-4 м²

γ=78 кН/м³ С=2 м F₂= 200·10^-4 м²

Е= 2·10⁵ МПа l/L =0,75 Р=1,5 кН

l =0,75 L=0,75·4=3м

Найти: построить эпюры N, σ, λ.
Решение: 1. Вычерчиваем расчетную схему, указав числовые значения размеров и нагрузки.

6,492

D
F₁


С 6,18

F₂

L Р 4,62

В 3,12
ℓ

С


А
2. Разбиваем брус на участки I-III и определяем величину внутреннего силового фактора на каждом участке. По полученным значениям строим эпюру продольных сил.

N^I = γ · F₂·z

при z=0 N^I =0 кН

z=С N^I = γ · F₂·С= 78· 200·10^-4 ·2 = 3,12 кН

N^II = γ · F₂·z + Р

при z=С N^II =3,12+1,5= 4,62 кН

z=ℓ N^I = γ · F₂·ℓ+P= 78· 200·10^-4 ·3+1,5 = 6,18 кН

N^III = γ · F₂·ℓ + Р + γ · F₁(z- ℓ)

при z= ℓ N^II =6,18 кН

z=L N^I = 6,18 + γ · F₁(L-ℓ)= 6,18+78· 40·10^-4 ·1 = 6,492 кН

3. Строим эпюру нормальных напряжений.

Участок I

при z=0 σ^I =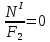

z=C σ^I =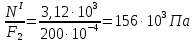

Участок II

при z=C σ^I =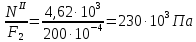

z=ℓ σ^I =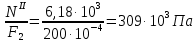

Участок III

при z=ℓ σ^I =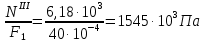

z=L σ^I =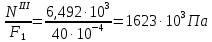

3. Определяем перемещение сечения, отстоящего от свободного конца бруса на расстоянии ℓ

Полное перемещение, согласно закону Гука: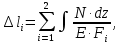



где Е – модуль продольной упругости материала (для стали Е=2·10⁵МПа).

Так величины определенных интегралов равны площадям, очерченным соответствующими подынтегральными функциями, то для вычисления перемещений достаточно вычислить площади эпюр N(z) на каждом участке и разделить их на EF.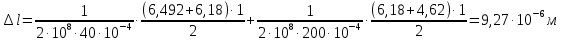