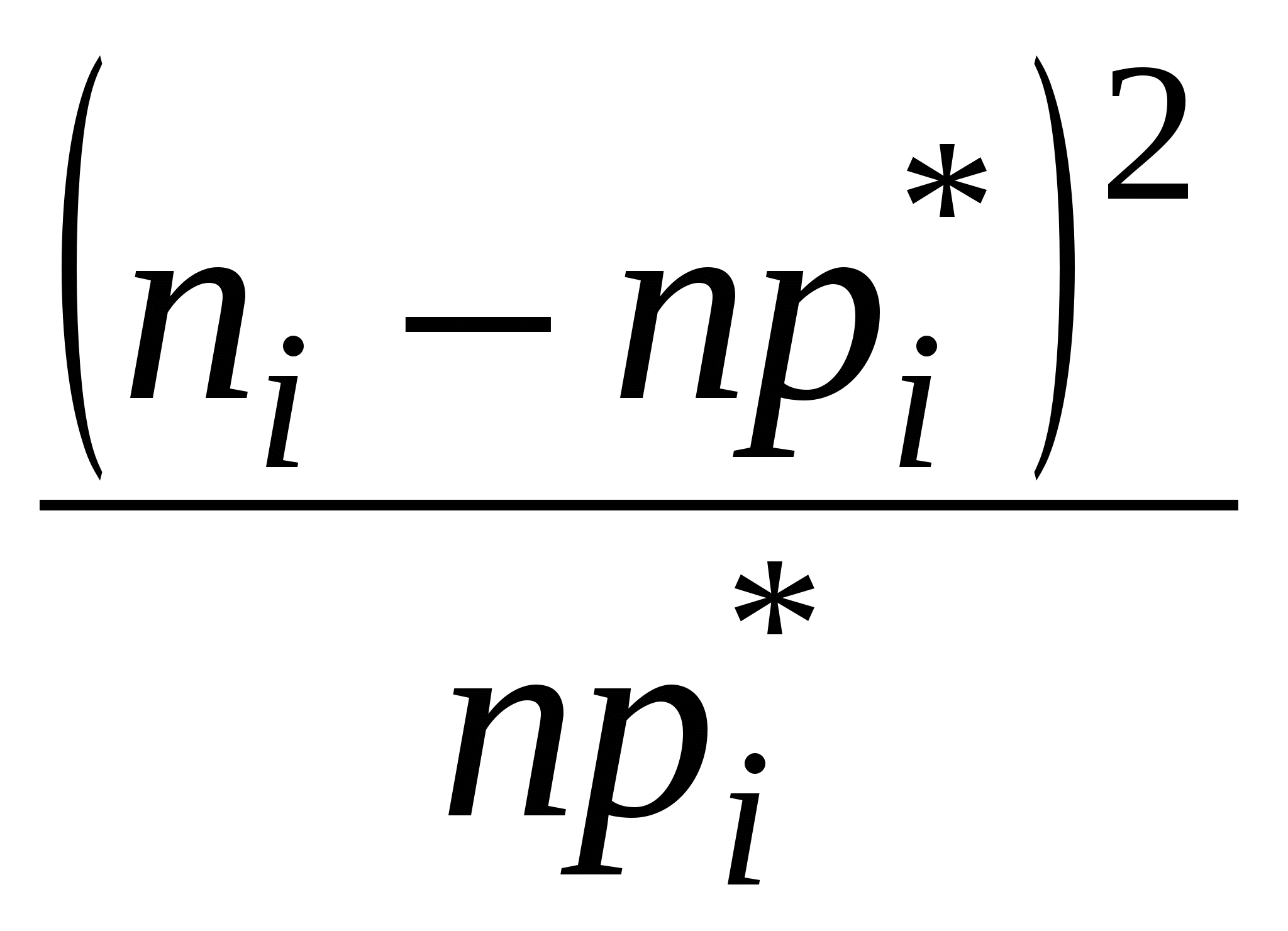Задача 1 Имеются выборочные данные 5%ного обследования распределения вкладчиков по размеру вклада в Сбербанке города
 Скачать 233 Kb. Скачать 233 Kb.
|
|
Задача №1 Имеются выборочные данные 5%-ного обследования распределения вкладчиков по размеру вклада в Сбербанке города:
Найти а) вероятность того, что средний размер вклада в Сбербанке отличается от его среднего размера в выборке не более чем на 5 тыс. руб. (по абсолютной величине); б) границы, в которых с вероятностью 0,95 заключена доля вкладов, размер которых менее 60 тыс. руб. в) объем повторной выборки, при котором те же границы для доли вкладов (см. п. б), можно гарантировать с вероятностью 0,9876. Дать ответ на тот же вопрос, если никаких предварительных данных о рассматриваемой доле нет. Решение:
Математическое ожидание: Дисперсия Среднеквадратическое отклонение а) Доверительный интервал для математического ожидания случайной величины с неизвестным законом распределения где По условию По таблице функции Лапласа найдем =2Ф(4,06)= 0,999952. Ответ: =0,999952. б) Найдем среднеквадратическую ошибку для доли выборки: здесь w – доля вкладов в выборке, размер которых менее 60 тыс. руб.: w=0,22. = 0,0332. w-= 0,1868. w+= 0,2532. Итак, границы, в которых с вероятностью 0,95 заключена доля вкладов, размер которых менее 60 тыс. руб.: в) объем выборки, при котором те же границы для доли предприятий, полученной в пункте б), можно гарантировать с вероятностью 0,9876. Объем бесповторной выборки определяется по формуле: По таблице находим 2Ф(t)=0,9876, t=2,245. При отсутствии предварительных данных о рассматриваемой доле используем формулу Задача №2 По данным задачи 1 требуется, используя критерий Решение: Математическое ожидание: несмещенная дисперсия Для расчета вероятностей Составим расчетную таблицу для вычисления эмпирического значения
Имеем: Так как Для построения графика рассчитаем относительные частоты 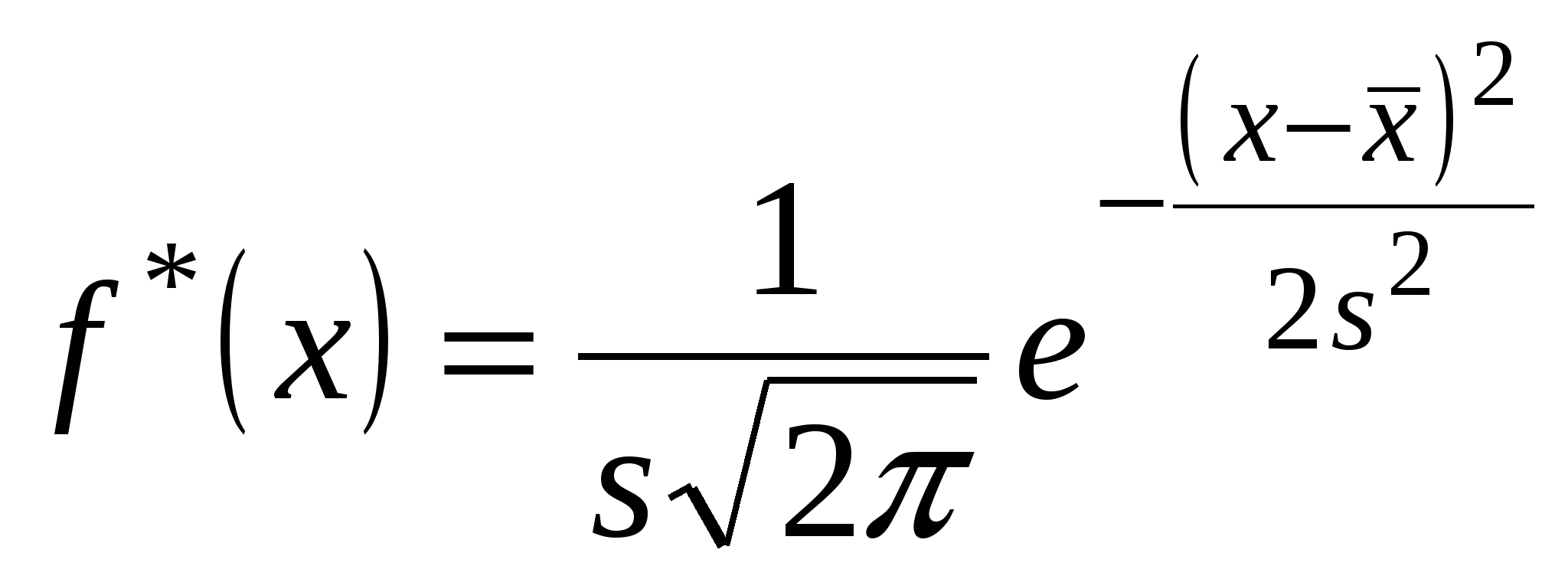 (см. расчетную таблицу). (см. расчетную таблицу).График 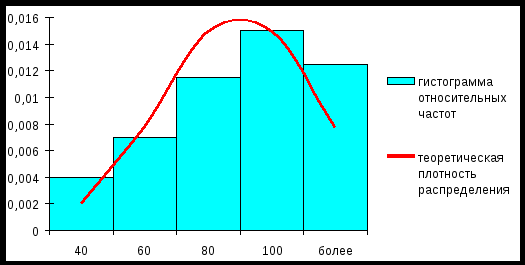 Задача №3 Распределение 110 предприятий по стоимости основных производственных фондов Х млн. руб. и стоимости произведенной продукции Y млн. руб. представлено в таблице:
Необходимо: 1. Вычислить групповые средние 2. предполагая, что между переменными Х и Y существует линейная корреляционная зависимость: а) найти уравнения прямых регрессии и построить их графики на одном чертеже с эмпирическими линиями регрессии; б) вычислить коэффициент корреляции, на уровне значимости а=0,05, оценить его значимость и сделать вывод о тесноте и направлении связи между переменными Х и Y; в) используя соответствующее уравнение регрессии, определить среднюю стоимость произведенной продукции, если стоимость основных производственных фондов составляет 45 млн. руб. Решение Групповые средние находим по формулам: 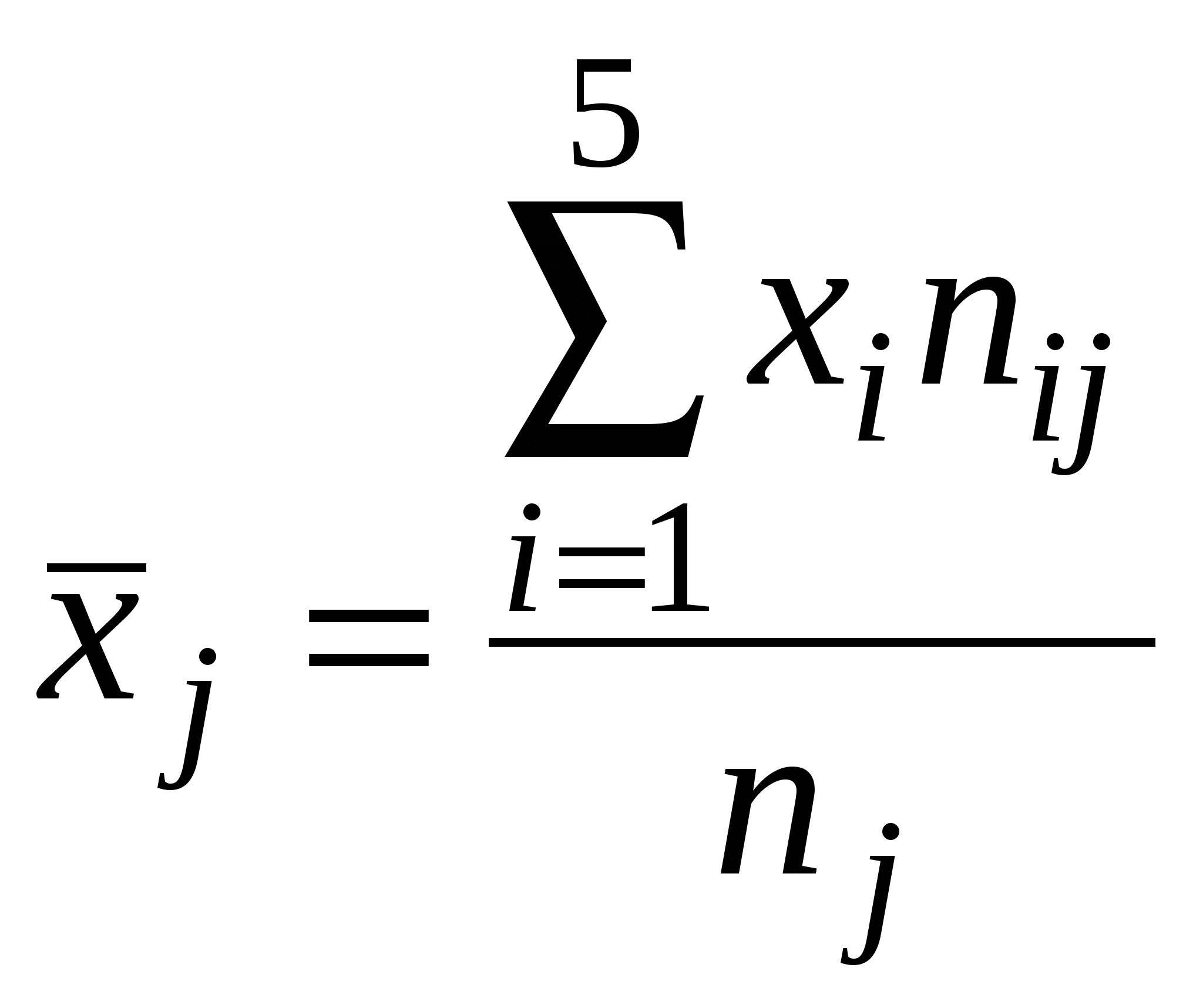 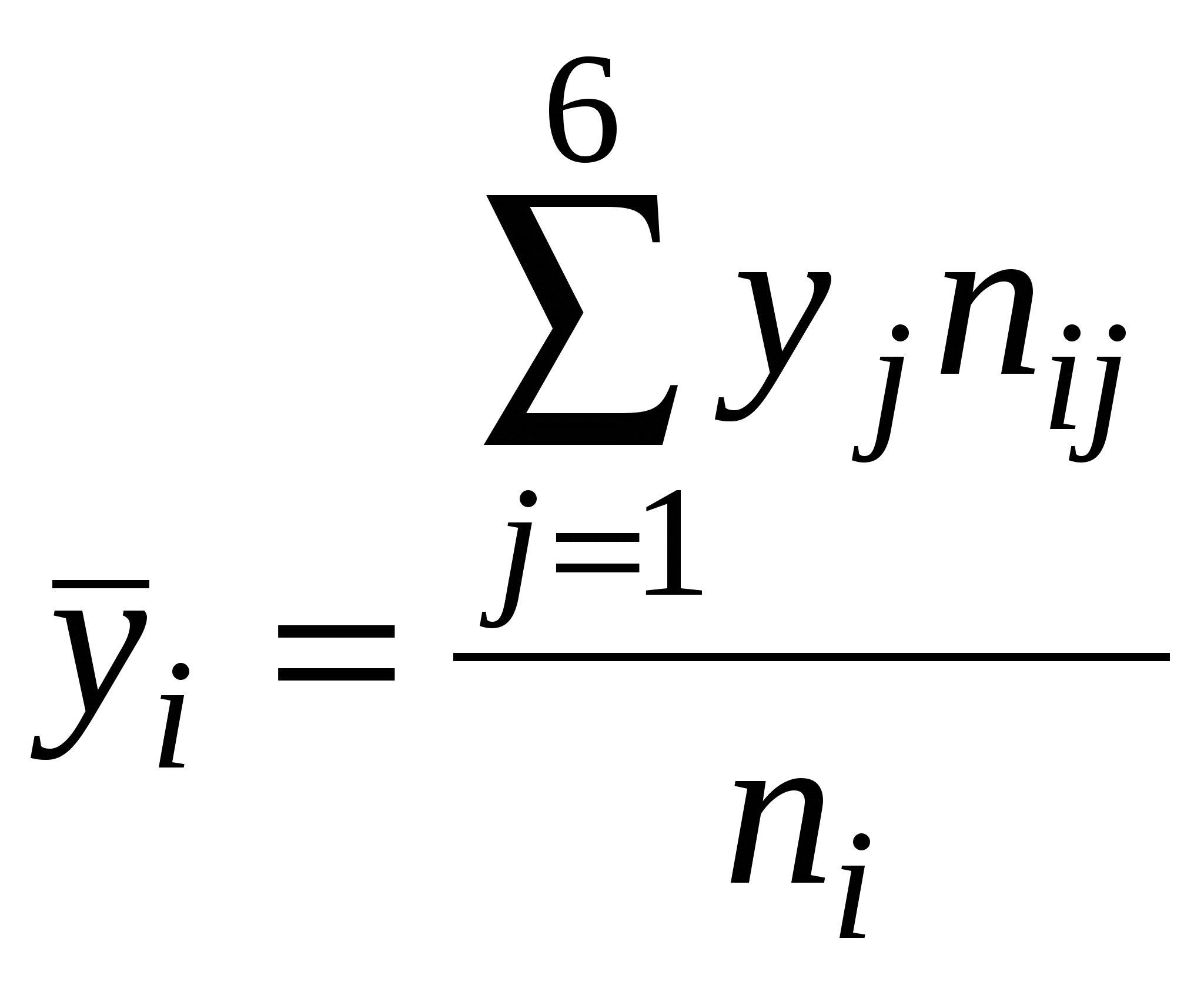 . Расчеты приведены в таблице: . Расчеты приведены в таблице:
Для нахождения уравнений регрессии вычисляем необходимые суммы: 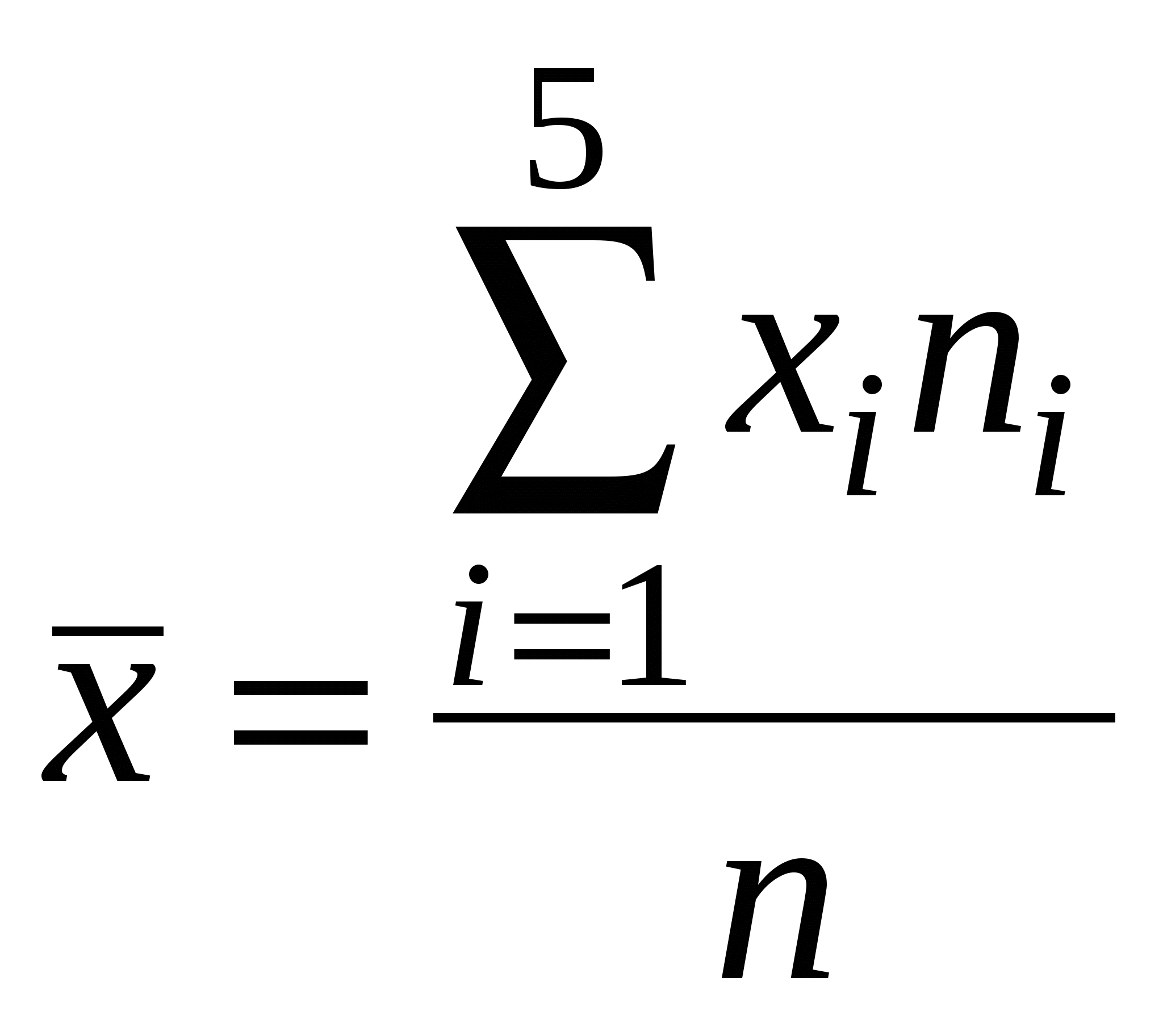 =29,727; =29,727; 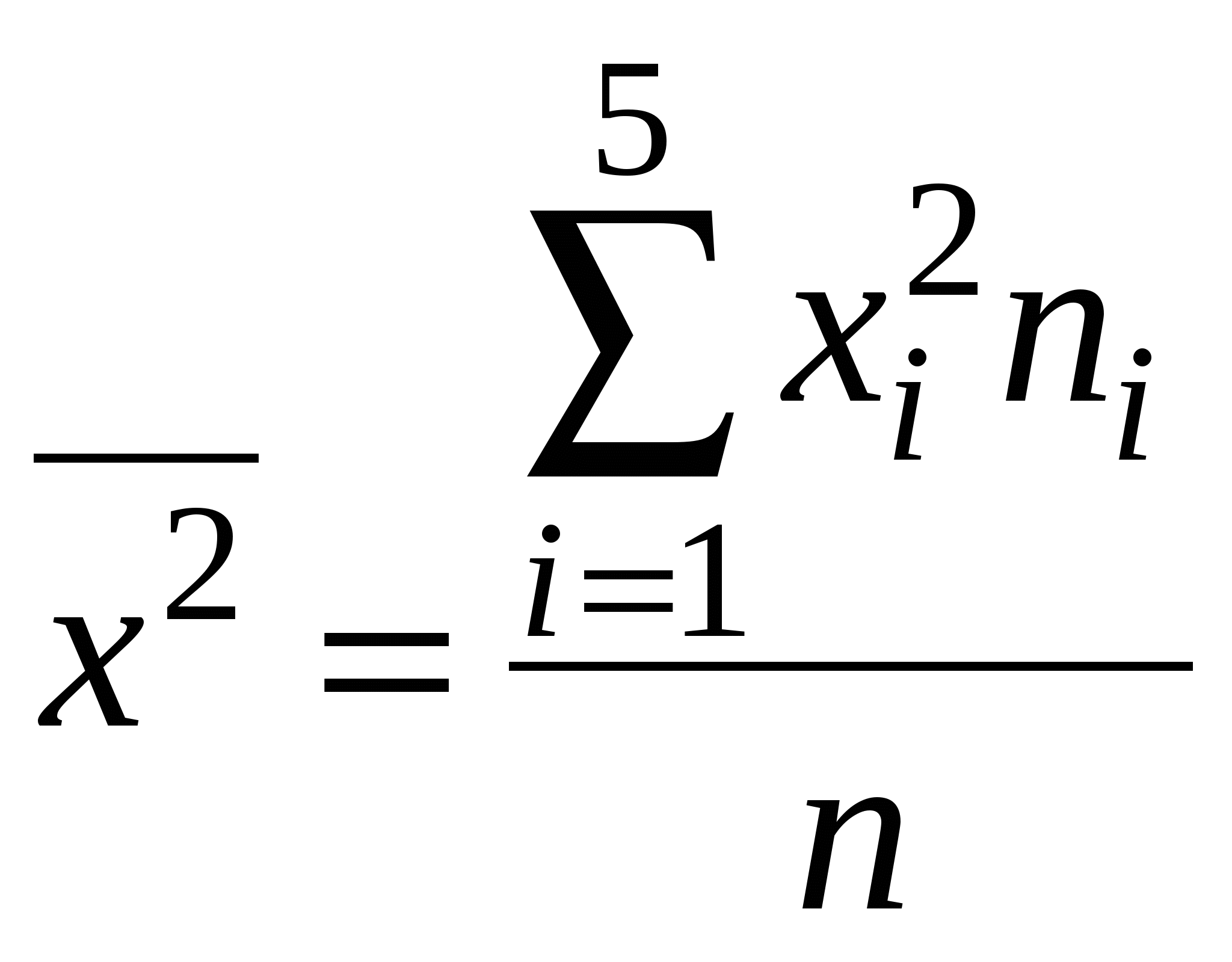 =1075,455; =1075,455;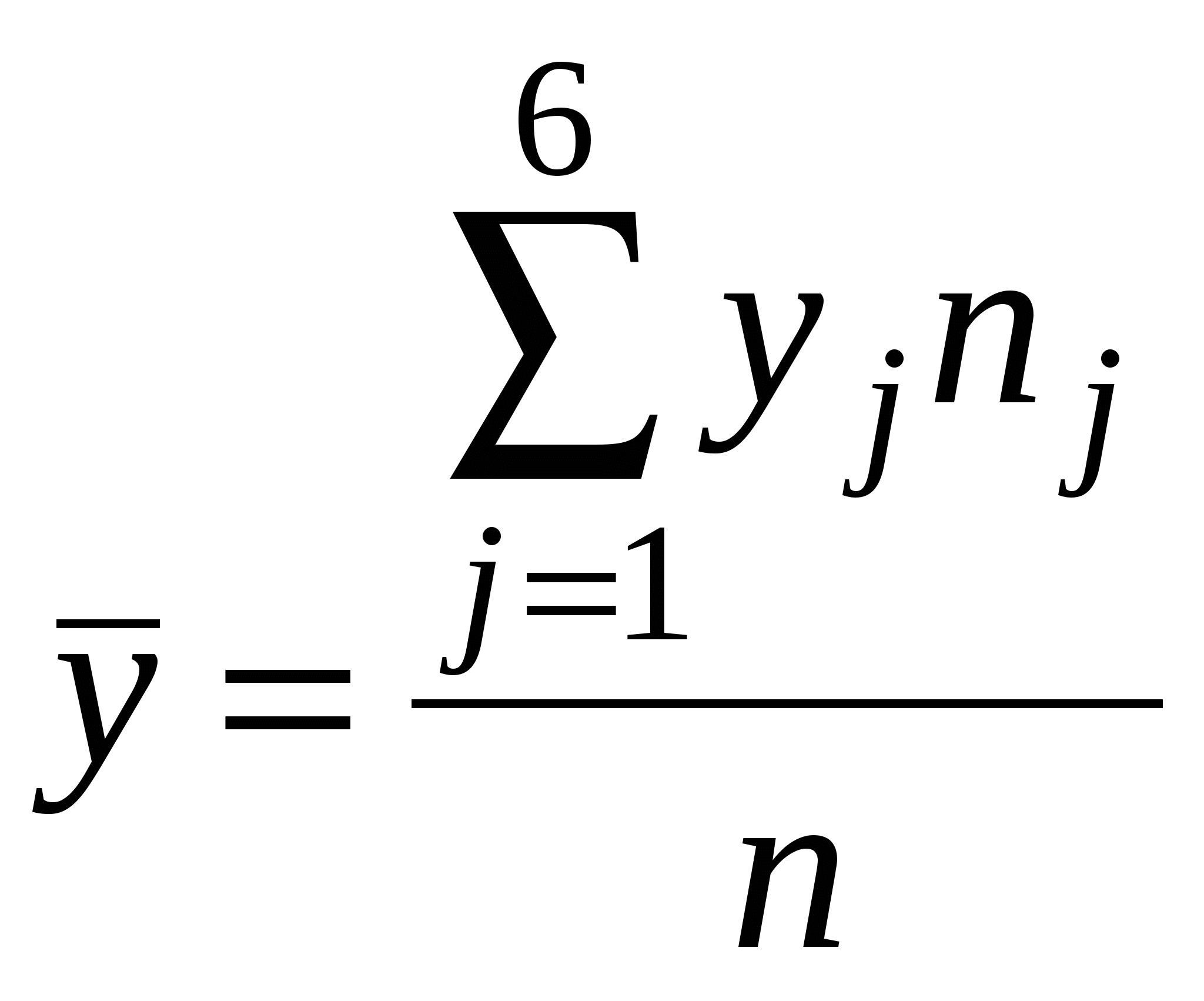 =42,000; =42,000; 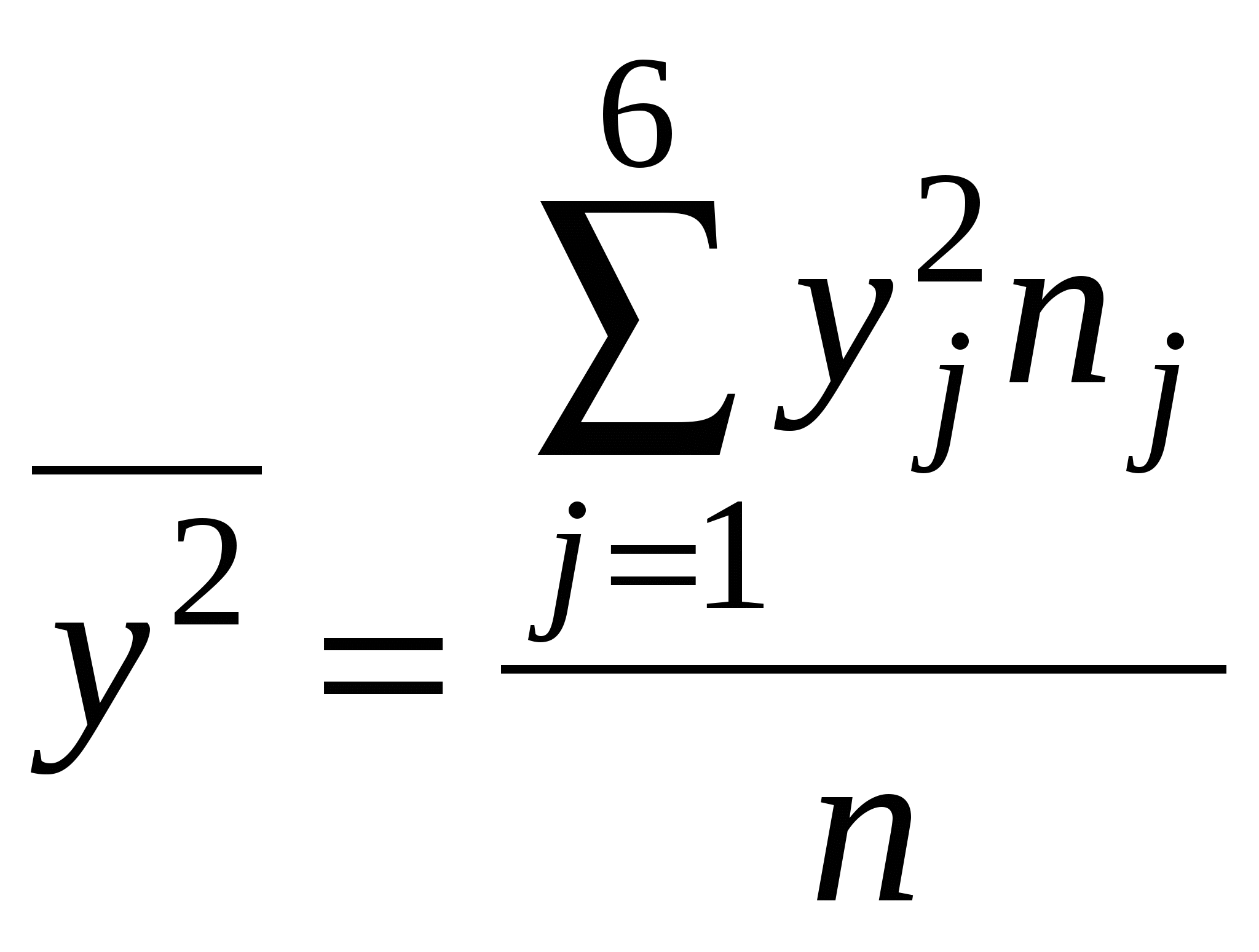 =2032,727; =2032,727;Уравнения регрессии: Ниже представлены графики полученных уравнений регрессии совместно с соответствующей эмпирической регрессией: 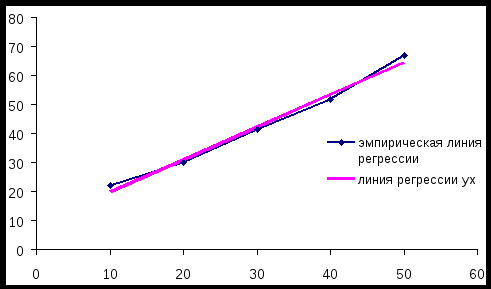 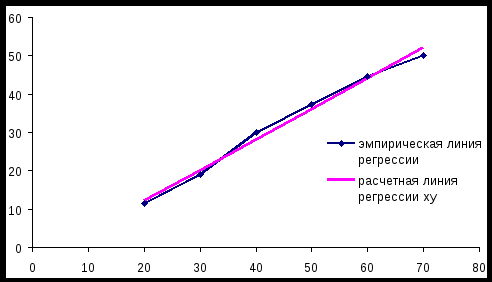 Находим коэффициент корреляции Оценим значимость коэффициента корреляции По таблице критерия Стьюдента для уровня значимости 0,05 находим Т.к. в) По найденному уравнению регрессии находим: Средняя стоимость произведенной продукции, если стоимость основных производственных фондов составляет 45 млн. руб. равна 59,06 млн. руб. |