Математика рчяды. Задача 1 Исследовать сходимость числовых рядов а б в г Решение а ряд с положительными членами
 Скачать 176.75 Kb. Скачать 176.75 Kb.
|
ПРАКТИЧЕСКОЕ ЗАДАНИЕ по дисциплине «Математика» _____________________________________________________
Москва 2022 Задача №1 Исследовать сходимость числовых рядов 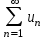 а) 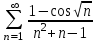 ; б) ; б) 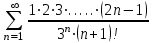 ; в) ; в) 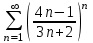 ; г) ; г) 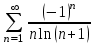 Решение: а) 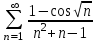 – ряд с положительными членами – ряд с положительными членамиПрименим признак сравнения. Рассмотрим ряд 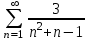 . Исследуем его сходимость с помощью признака Коши: . Исследуем его сходимость с помощью признака Коши: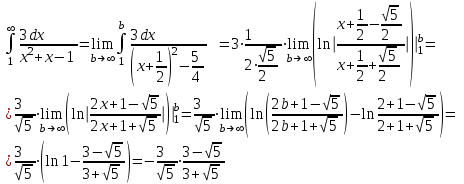 Так как несобственный интеграл сходится, то и сам ряд сходится. 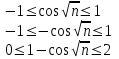 Тогда: 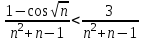 Так как больший ряд сходится, то и меньший тоже сходится. Ответ: ряд сходится б) 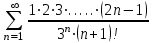 – ряд с положительными членами – ряд с положительными членами Применим для исследования признак Даламбера: 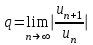 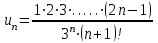 ; ; 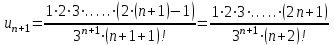 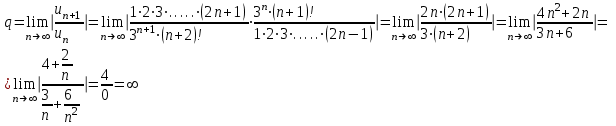 Так как Так как 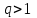 , то ряд расходится , то ряд расходитсяОтвет: ряд расходится. в) 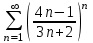 – ряд с положительными членами – ряд с положительными членами Используем необходимый признак сходимости ряда: 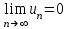 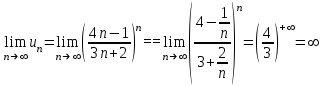 Так как 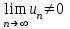 , то ряд расходится. , то ряд расходится.Ответ: Ряд расходится г) 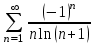 – знакочередующийся ряд – знакочередующийся рядПрименим признак Лейбница: Если в знакочередующемся ряде абсолютные величины членов убывают, а общий член ряда стремится к нулю, то ряд сходится. 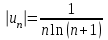 1) последовательность, составленная из модулей членов ряда убывающая: 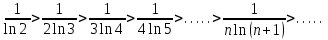 2) 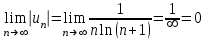 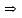 ряд сходится. ряд сходится.Исследуем ряд на абсолютную сходимость. Знакопеременный ряд сходится абсолютно, если сходится ряд из абсолютных величин его членов. Исследуем на сходимость ряд 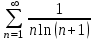 . . Применим признак сравнения: Рассмотрим ряд 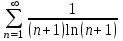 . Исследуем его на сходимость с помощью интегрального признака Коши: . Исследуем его на сходимость с помощью интегрального признака Коши: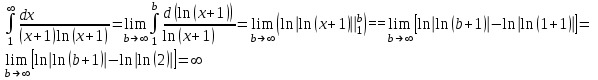 так как несобственный интеграл расходится, то и ряд 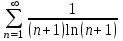 расходится. расходится.так как для всех n: 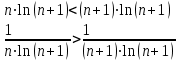 Так как ряд 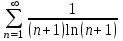 расходится, то больший ряд расходится, то больший ряд 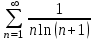 соответственно тоже расходится. То есть знакочередующийся ряд сходится условно. соответственно тоже расходится. То есть знакочередующийся ряд сходится условно.Ответ: ряд сходится условно. Задание 2 Найти интервал сходимости степенного ряда. Исследовать сходимость ряда на концах интервала а) 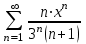 ; б) ; б) 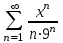 Решение: а) 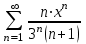 ; ; Найдем радиус сходимости ряда: 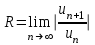 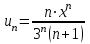 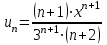 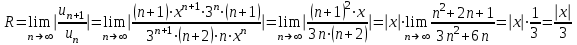 Данный ряд сходится при всех значениях х, удовлетворяющих неравенству: 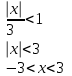 Исследуем сходимость ряда на концах данного интервала: При 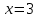 имеем ряд имеем ряд 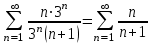 – ряд с положительными членами. – ряд с положительными членами. Исследуем этот ряд с помощью необходимого признака сходимости: 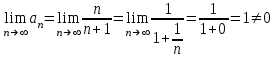 Необходимое условие сходимости ряда не выполняется, следовательно, ряд расходится и 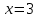 не входит в область сходимости ряда. не входит в область сходимости ряда.При 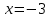 имеем ряд имеем ряд 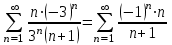 – знакочередующийся ряд. – знакочередующийся ряд.Применим признак Лейбница: Если в знакочередующемся ряде абсолютные величины членов убывают, а общий член ряда стремится к нулю, то ряд сходится. 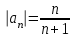 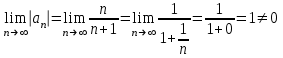 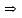 ряд расходится. ряд расходится.То есть, при 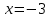 исходный степенной ряд также расходится. исходный степенной ряд также расходится.Таким образом, 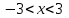 – область сходимости степенного ряда. – область сходимости степенного ряда. Ответ: 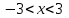 б) 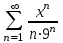 ; ; Найдем радиус сходимости ряда: 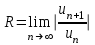 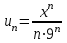 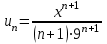 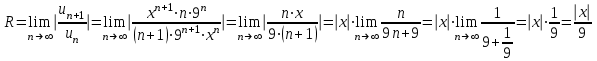 Данный ряд сходится при всех значениях х, удовлетворяющих неравенству: Данный ряд сходится при всех значениях х, удовлетворяющих неравенству: 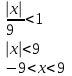 Исследуем сходимость ряда на концах данного интервала: При 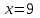 имеем ряд имеем ряд 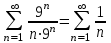 – гармонический ряд. – гармонический ряд.Данный ряд является расходящимся, поэтому 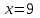 не входит в область сходимости ряда. не входит в область сходимости ряда.При 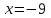 имеем ряд имеем ряд 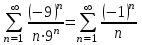 – знакочередующийся ряд. – знакочередующийся ряд.Применим признак Лейбница: Если в знакочередующемся ряде абсолютные величины членов убывают, а общий член ряда стремится к нулю, то ряд сходится. 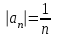 – члены ряда убывают по абсолютному значению – члены ряда убывают по абсолютному значению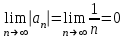 . .так как абсолютная величина члена ряда стремится к 0 при 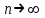 , то ряд сходится. То есть при , то ряд сходится. То есть при 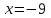 исходный степенной ряд сходится. Так как ряд из модулей расходится, то ряд сходится условно. исходный степенной ряд сходится. Так как ряд из модулей расходится, то ряд сходится условно.Таким образом, 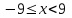 – область сходимости степенного ряда. – область сходимости степенного ряда.Ответ: 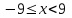 Задача № 3 Вычислить определенный интеграл 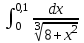 с точностью до 0,001 путем разложения подынтегральной функции в степенной ряд и почленного интегрирования полученного ряда. с точностью до 0,001 путем разложения подынтегральной функции в степенной ряд и почленного интегрирования полученного ряда.Решение: Разложим подынтегральную функцию в биномиальный ряд по степеням x: Используем разложение функции в ряд: 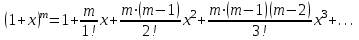 , где , где 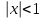 Так как отрезок интегрирования [0; 0,1] находится внутри интервала сходимости биноминального ряда, то ряд можно почленно интегрировать. Подставляя в интеграл, вышеприведенное разложение подынтегральной функции и почленно интегрируя в указанных пределах, получаем 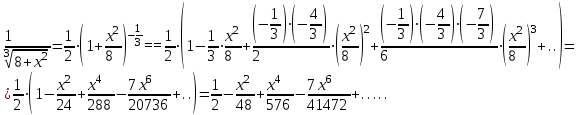 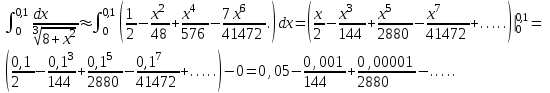 Второй член 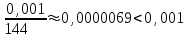 . Поэтому для вычисления приближенного значения интеграла с требуемой точностью достаточно ограничиться только первым членом ряда: . Поэтому для вычисления приближенного значения интеграла с требуемой точностью достаточно ограничиться только первым членом ряда: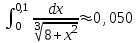 Ответ: 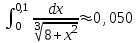 Задание№4 Найти три первых, отличительных от нуля, члена разложения в степенной ряд решение 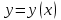 дифференциального уравнения дифференциального уравнения 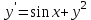 , удовлетворяющего условию , удовлетворяющего условию 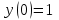 Решение: Ищем решение в виде ряда: 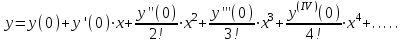 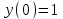 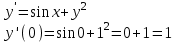 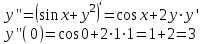 Получили три ненулевых коэффициента, теперь найдем разложение решения: 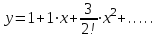 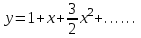 Ответ: 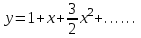 Задание №5. Разложить в ряд Фурье периодическую функцию, заданную на полупериоде 0, l по косинусам. Построить график функции и график суммы полученного ряда Фурье 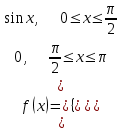 Функцию 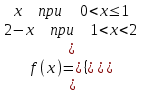 разложить по косинусам кратных дуг. разложить по косинусам кратных дуг.Решение: Продолжим данную функцию четным образом на отрезок [–  ; 0], то есть рассмотрим функцию ; 0], то есть рассмотрим функцию 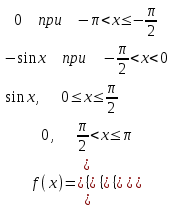 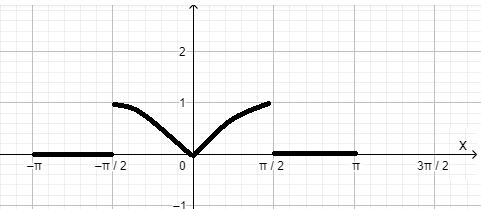 Ряд Фурье для четной функции имеет вид: 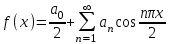 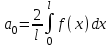 ; ; 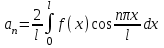 ; ; 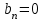 Найдем коэффициенты функции: 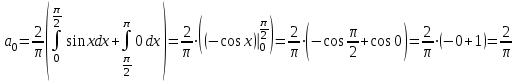 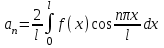 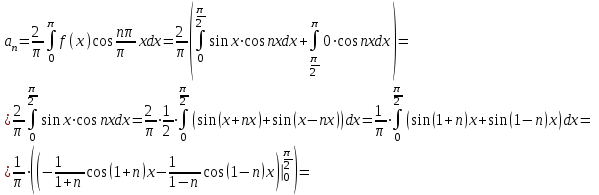 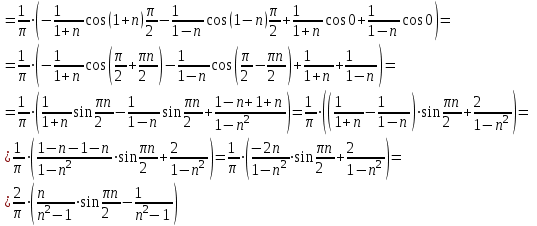 Ряд косинусов для функции 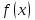 имеет вид: имеет вид: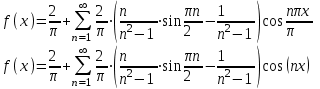 Изобразим схематически график ряда Фурье: 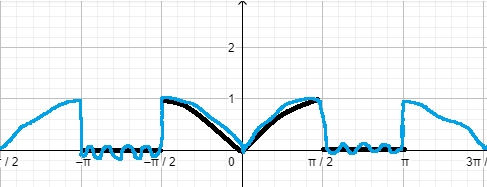 Ответ: 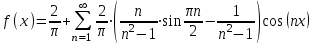 |

