Эконометрика 1 контрольная. Задача 1 Исследуя спрос на продукцию фирмы, аналитический отдел собрал данные по 20 торговых точках компании и представил их в виде (2,7) (2,8) где y объем спроса, х цена единицы продукции в скобках приведены фактические значения tкритерия.
 Скачать 43.09 Kb. Скачать 43.09 Kb.
|
|
Задача 1 Исследуя спрос на продукцию фирмы, аналитический отдел собрал данные по 20 торговых точках компании и представил их в виде: 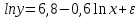 (2,7) (-2,8) где y – объем спроса, х – цена единицы продукции В скобках приведены фактические значения t-критерия. Ранее предполагалось, что увеличение цены на 1% приводит к уменьшению спроса на 1,2%. Можно ли утверждать, что приведенные результаты подтверждают это предположение? Решение: Уравнение регрессии в прологарифмированном виде. Судя по форме записи, уравнение имеет степенной вид и записывается так: 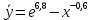 Надо провести предположение о том, что эластичность спроса по цене равна -1,2. В степенной зависимости эластичность равна показателю степени b, поэтому оценка эластичности равна -0,6. Таким образом, задача сводится к проверке статистической гипотезы (нуль-гипотезы) H0: b= - 1,2 против альтернативной H1: b≠ -1,2. Критическая область двусторонняя, поэтому проверка гипотезы может быть заменена построением доверительного интервала для b и, если проверяемое значение b = -1,2 попадает в него, то нуль-гипотеза не отклоняется; в противном случае принимается альтернативная гипотеза. 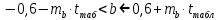 Определим стандартную ошибку параметра b из формулы: 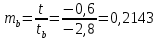 Для определения tтабл зададим уровень значимости, равный 0,05, следовательно: 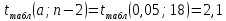 (используем таблицу критических точек распределения Стьюдента для двухстороннего a=0,05). Доверительный интервал равен: 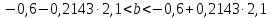 или 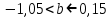 Значение, равное -1,2, в интервал не попадает, следовательно, предположение о значении коэффициента эластичности на уровне значимости 0,05 следует отклонить. Однако, если задать значимость на уровне 0,01, то tтабл=2,88, и интервал будет таким: 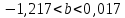 Следовательно, на уровне значимости 0,01 первоначальное предположение не может быть отклонено, поскольку значение -1,2 попадает в доверительный интервал. Можно проверить статистическую гипотезу напрямую, вычислив t – статистику для разницы между гипотетическим и вычисленным значениям b: 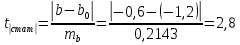 Сравним полученную статистику по абсолютной величине с критическим значением на заданном уровне значимости. На уровне a = 0,05: 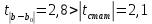 Нуль-гипотеза отклоняется, эластичность спроса по цене не может быть равна -1,2. На уровне a = 0,01: 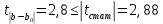 Нуль-гипотеза не отклоняется, эластичность может быть равна -1,2. Задача 2 По совокупности 18 предприятий торговли изучается зависимость между ценой х на некоторый товар и прибылью у торгового предприятия. При оценке регрессионной модели были получены следующие результаты: 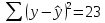 ; ; 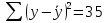 Проверить статистическую значимость уравнения регрессии. Построить таблицу дисперсионного анализа. Решение: В условиях задачи n = 18; остаточная СКО равна 23, а общая СКО – 35. Для расчета индекса корреляции воспользуемся выражением: 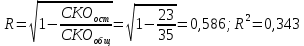 Фактическое значение F-критерия рассчитаем с помощью выражения: 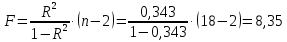 При проверке статистической значимости уравнения в целом воспользуемся F-критерием и сравним его с критическим значением, задавшись уровнем значимости 0,05. Табличное (критическое) значение при этом равно: 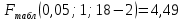 Поскольку фактическое значение, равное 8,35, больше критическое, нуль-гипотезу о статистической незначимости уравнения регрессии следует отклонить, и уравнение на уровне а = 0,05 является значимым; статистическая связь между y и x считается доказанной. Однако, если задать а = 0,01, то: 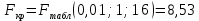 И в этом случае нуль-гипотезу отклонить нельзя, на уровне а = 0,01 уравнение не значимо. Для построения таблицы дисперсионного анализа определим из балансового уравнения величину факторной СКО: 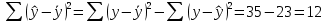 Поскольку мы имеем дело с парной регрессионной зависимостью, число степеней свободы факторной СКО принимаем равным единице. С учетом этих условий таблица дисперсионного анализа выглядит следующим образом:
Задача 3 Уравнение регрессии, построенное по 17 наблюдениям, имеет вид: 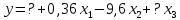 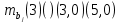 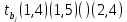 Расставить пропущенные значения, а также построить доверительный интервал для b2 с вероятностью 0,99 Решение: Пропущенные значения определяем с помощью формулы: 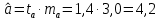 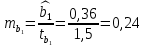 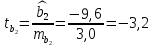 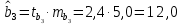 Таким образом, уравнение регрессии со статистическими характеристиками выглядит так: 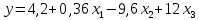 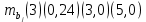 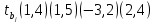 Строим доверительный интервал для b2. Здесь уровень значимости равен 0,01, а число степеней свободы равно n – p – 1 = 17 – 3 – 1 = 13, где n = 17 – объем выборки, p = 3 – число факторов в уравнении регрессии. Отсюда t(0,01; 13) = 3,0123; 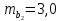 ; ; 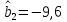 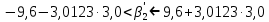 Или 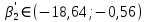 Этот доверительный интервал накрывает истинное значение параметра 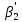 с вероятностью, равной 0,99. с вероятностью, равной 0,99.Задача 4 По некоторым переменным имеются следующие статистические данные: 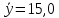 ; ; 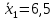 ; ; 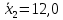 ; ; 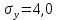 ; ; 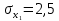 ; ; 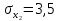 ; ; 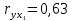 ; ; 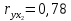 ; ; 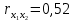 Построить уравнение регрессии в стандартизированном и натуральном масштабах. Решение: Поскольку изначально известны коэффициенты парной корреляции между переменными, начать следует с построения уравнения регрессии в стандартизированном масштабе. Для этого надо решить систему нормальных уравнений, которая в случае двух факторов имеет вид: 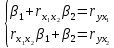 Или, после подстановки исходных данных: 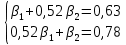 Решаем эту систему уравнений любым способом и получаем: β1= 0,3076, β2 = 0,62. Запишем уравнение регрессии в стандартизированном масштабе: 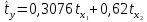 Теперь перейдем к уравнению регрессии в натуральном масштабе, для чего используем формулы: 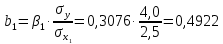 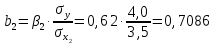 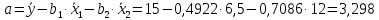 Уравнение регрессии в натуральном масштабе имеет вид: 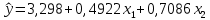 |