Решение. Задача 1 Известно математическое ожидание а (mn) и среднее квадратическое отклонение n нормально распределенной случайной величины Х. Найти вероятность попадания этой величины в заданный интервал (mn1,mn2)
 Скачать 125.78 Kb. Скачать 125.78 Kb.
|
|
Задача 1 Известно математическое ожидание а = (m+n) и среднее квадратическое отклонение 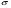 =n нормально распределенной случайной величины Х. Найти вероятность попадания этой величины в заданный интервал (m+n-1,m+n+2). =n нормально распределенной случайной величины Х. Найти вероятность попадания этой величины в заданный интервал (m+n-1,m+n+2). Для заданной выборки, прибавив m к каждому члену ряда, составить: 1. Безинтервальный вариационный ряд 2. Равноинтервальный вариационный ряд, разбив выборку на k интервалов. 3. Построить гистограмму распределения 4. Найти числовые характеристики вариационного ряда:
Доверительный интервал для генеральной средней, при уровне значимости 0,05 Таблица 1
Решение:
1. Составим безинтервальный вариационный ряд Для этого подсчитаем количество повторения для каждого элемента ряда.
2. Равноинтервальный вариационный ряд, разбив выборку на k интервалов. Определим число групп. Число групп приближенно определяется по формуле Стэрджесса k = 1 + 3,2log n = 1 + 3,2log(30) = 6 Ширина интервала составит: 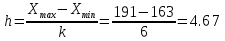 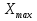 - максимальное значение группировочного признака в совокупности. - максимальное значение группировочного признака в совокупности. 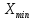 - минимальное значение группировочного признака. - минимальное значение группировочного признака. Определим границы группы.
Одно и тоже значение признака служит верхней и нижней границами двух смежных (предыдущей и последующей) групп. Для каждого значения ряда подсчитаем, какое количество раз оно попадает в тот или иной интервал. Для этого сортируем ряд по возрастанию.
Результаты группировки оформим в виде таблицы:
3. Построим гистограмму распределения 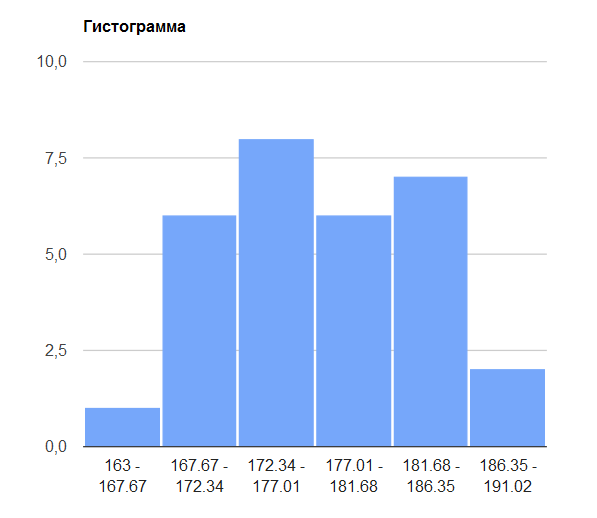 4. Найдем числовые характеристики вариационного ряда: Таблица для расчета показателей.
Выборочная средняя арифметическая, Эмпирическая функция распределения 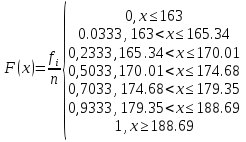 Выборочная дисперсия Выборочное среднее квадратическое отклонение Мода. где x0 – начало модального интервала; h – величина интервала; f2 –частота, соответствующая модальному интервалу; f1 – предмодальная частота; f3 – послемодальная частота. Выбираем в качестве начала интервала 172.34, так как именно на этот интервал приходится наибольшее количество. Наиболее часто встречающееся значение ряда – 174.68 Медиана. Таким образом, 50% единиц совокупности будут меньше по величине 177.01. Доверительный интервал для генеральной средней, при уровне значимости 0,05 Определяем значение tkp по таблице распределения Стьюдента По таблице Стьюдента находим: Tтабл(n-1;α/2) = Tтабл(29;0.025) = 2.045 (177.48 - 2.32;177.48 + 2.32) = (175.16;179.8) С вероятностью 0.95 можно утверждать, что среднее значение при выборке большего объема не выйдет за пределы найденного интервала. Задача 2 Случайные величины 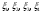 имеют равномерное, пуассоновское и показательное и нормальное распределение распределения соответственно. Известно, что математические ожидания имеют равномерное, пуассоновское и показательное и нормальное распределение распределения соответственно. Известно, что математические ожидания 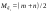 , а дисперсия , а дисперсия 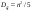 . Построить графики случайных величин . Построить графики случайных величинРешение Дискретные случайные величины Для пуассоновского распределения 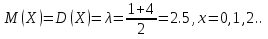 Берем 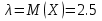 Непрерывные случайные величины Для равномерного распределения 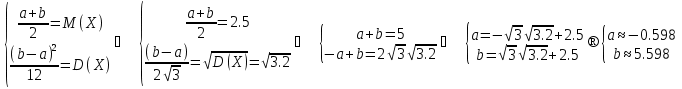 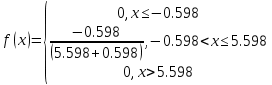 Для показательного распределения 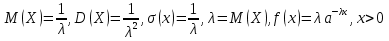 берем, M(X)=2.5, 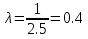 Для нормального распределения 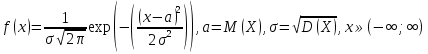 берем M(X)=2.5, 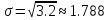 Задача 3. Результаты ЕГ по школе №2 представлены в таблице 2. Найти числовые характеристики дискретной случайной величины Х: выборочное среднее Считая, что случайная величина Х (количество баллов) распределена нормально, с надежностью Таблица 2
Решение: Таблица для расчета показателей.
выборочное среднее выборочная дисперсия выборочное среднее квадратическое отклонение 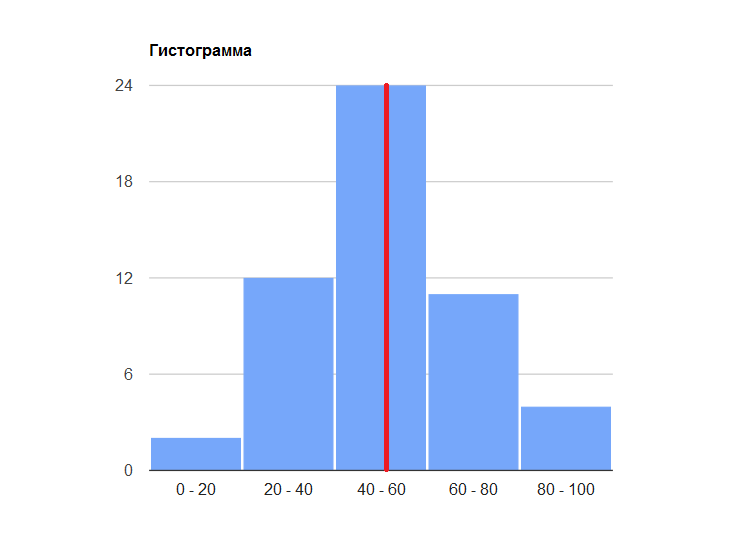 Доверительный интервал для генерального среднего. В этом случае 2Ф(tkp) = γ Ф(tkp) = γ/2 = 0.95/2 = 0.475 По таблице функции Лапласа найдем, при каком tkp значение Ф(tkp) = 0.475 tkp(γ) = (0.475) = 1.96 (51.13 - 5.11;51.13 + 5.11) = (46.02;56.24) С вероятностью 0.95 можно утверждать, что среднее значение при выборке большего объема не выйдет за пределы найденного интервала. Задача 4. Для проверки результативности новой методики были проведены контрольные работы в двух равных по силе классах. Результаты представлены в таблице 3. На уровне значимости Таблица 3
Решение Рассчитываем выборочные средние и исправленные среднеквадратические отклонения по формулам Выборочное среднее 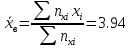 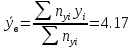 Расчеты приведены в таблице
Выборочная дисперсия 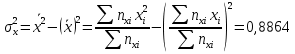 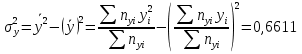 Исправленная выборочная дисперсия 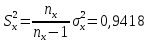 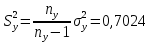 Исправленное выборочное среднее квадратическое отклонение 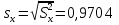 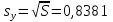 Выборочные средние не равны 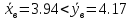 Нулевая гипотеза Конкурирующая гипотеза Считаем совокупности распределенными нормально с неизвестными, но одинаковыми дисперсиями. Рассчитываем наблюдаемое значение критерия. 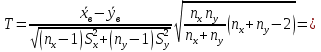 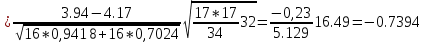 Для уровня значимости 0,95 и числа степеней свободы 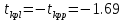 Так как 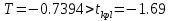 , то нулевую гипотезу не отвергаем. Следовательно, улучшения успеваемости не так велики и методику следует усовершенствовать. , то нулевую гипотезу не отвергаем. Следовательно, улучшения успеваемости не так велики и методику следует усовершенствовать.Задача 5. В таблице 5 приведены данные по урожайности картофеля на школьном опытном участке по годам. Таблица 5
По данным таблицы методом наименьших квадратов: а) найти коэффициент корреляции и вычислить регрессии 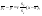  б) построить корреляционное поле и линии регрессий, в) найти доверительные интервалы для  =M(r) и =M(r) и 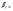 =M( =M(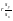 ) )г) проверить гипотезу о значимости выборочного коэффициента корреляции. Решение Расчеты приведены в таблице
Выборочное среднее 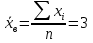 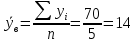 Выборочная дисперсия 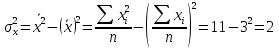 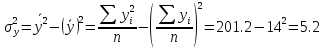 Выборочное среднее квадратическое отклонение 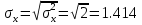 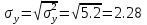 Среднее значение Выборочный коэффициент корреляции 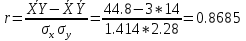 Уравнение линейной регрессии 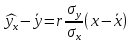 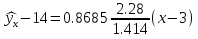 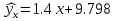 Расчетные значения линейной регрессии урожайности приведены в последнем столбце таблицы Корреляционное поле и линия регрессии представлены на рис Найдем доверительные интервалы для ρ=M(r) и 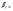 =M( =M(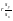 ) )По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=3 находим tкрит: tкрит (n-m-1;α/2) = (3;0.025) = 3.182 где m = 1 - количество объясняющих переменных. Доверительный интервал для ρ=M(r). (-0.0432;1) Доверительный интервал для 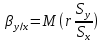 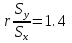 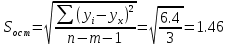 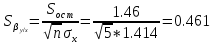 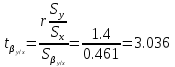 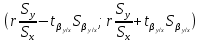 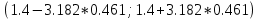 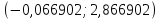 Проверка гипотезы о значимости выборочного уравнения регрессии корреляции. Нулевая гипотеза 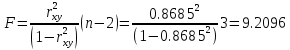 По уровню значимости 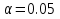 и находим критическое значение критерия Фишера и находим критическое значение критерия Фишера Так как 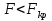 принимаем нулевую гипотезу о равенстве 0 коэффициента корреляции принимаем нулевую гипотезу о равенстве 0 коэффициента корреляции |
