Таблица 15. -
= у3
|
0
|
1
|
2
|
3
|
F2 (= y3)
|
30
|
44
|
59
|
77
|
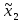 (= y3) (= y3)
|
2
|
2
|
3
|
3
|
Переходим к следующему этапу. Полагаем k=3 и табулируем функцию
F3 ( = y4):
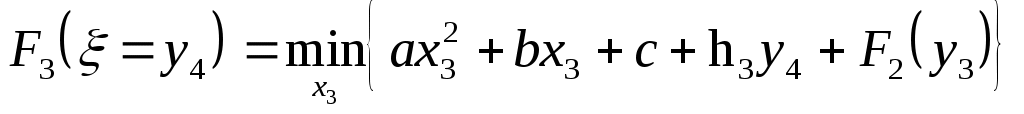
Вычисляем значение функции состояния только для одного значения аргумента = у4 = 0, так как не хотим оставлять продукцию в запас в конце исследуемого периода. Процесс вычислений приведен в табл. 16. Получаем
F3 ( = y4) = min 3 (x3,0) = min (81, 68, 62, 61) = 61,
x3
минимум достигается при значении переменной х3, равной
 3 ( = y4 = 0) = 3. 3 ( = y4 = 0) = 3.
Таким образом, мы получили не только минимальные общие затраты на производство и хранение продукции, но и последнюю компоненту оптимального решения. Она равна
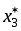 = 3. = 3.
Остальные компоненты оптимального решения найдем по обычным правилам метода динамического программирования. Чтобы найти предпоследнюю компоненту, учтем, что
х3 + у3 - d3 = y4
или
3 + у3 - 3 = 0,
откуда
у3 = 0.
Из таблицы 15 находим значение 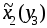
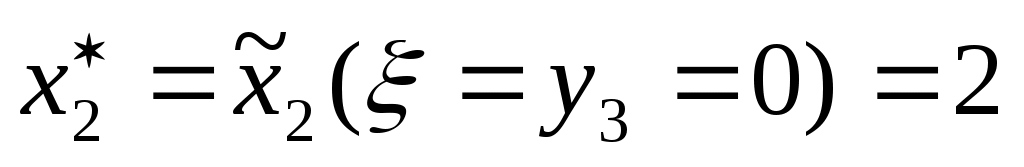
Аналогично, продолжая двигаться в обратном направлении и учтя, что
х2 + у2 - d2 = y3
или
2 + у2 - 3 = 0,
получаем
у2 = 1;
из таблицы 13 находим значение х1()
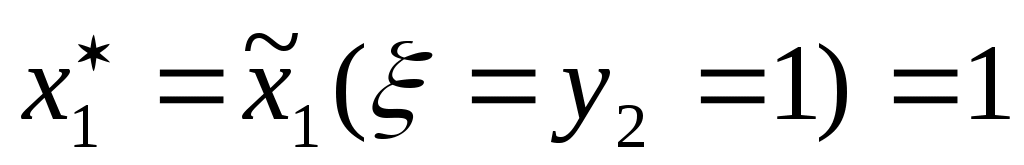 . .
Итак, оптимальный план производства имеет вид
х1 = 1
х2 = 2
х3 = 3,
а минимальные общие затраты составляют 61 единицы.
Сделаем проверку полученного результата. Для этого по исходным данным и найденному плану производства заполняем таблицу 17 и убеждаемся, что заявки потребителей на каждом этапе выполняются
у1 + х1 d1 у2 + х2 d2 у3 + х3 d3
2 + 1 2 1 + 2 3 0 + 3 3
и что суммарный объем производства и имевшегося к началу первого этапа запаса продукции равен суммарной потребности
у1 + х1 + х2 + х3 = d1 + d2 + d3
2 + 1 + 2 + 3 = 2 + 3 + 3
причем это достигается при наименьших возможных затратах на производство и хранение продукции
(х1) + (х2) + (х3) + h1у2 + h2у3 = F3(y4=0)
(2∙12 + 3∙1 + 4) + (2∙22 + 3∙2 + 4) + (2∙32 + 3∙3 + 4) + 3∙1 + 2∙0 =
= 9 + 18 + 31 + 3 + 0 = 61
K=2
Таблица 14.
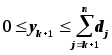
|
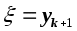
|
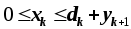
|
xk
|
yk = yk+1 + dk - xk
|
k(xk, yk+1) =k(xk) + hkyk+1 + Fk-1(yk)
|
0 y3 d3
|
= y3
|
0 x2 d2 + y3
|
x2
|
y2 = y3 + d2 - x2
|
2(x2, y3) = a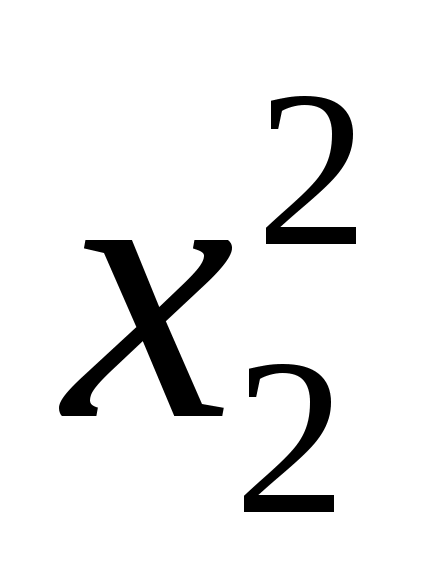 + bx + c + h2y3 + F1(y2) + bx + c + h2y3 + F1(y2)
|
0 y3 3
|
= y3
|
0 x2 3 + y3
|
x2
|
y2 = y3 + 3 - x2
|
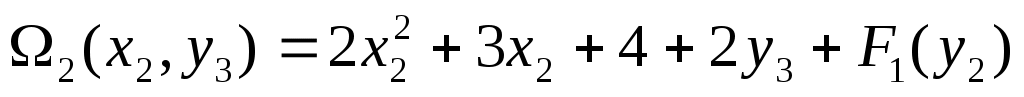
|
|
y3 = 0
|
0 x2 3
|
x2 = 0
x2 = 1
x2 = 2
х2 = 3
|
y2 = 3 - 0 = 3
y2 = 3 - 1 = 2
y2 = 3 - 2 = 1
у2 = 3 - 3 = 0
|
2(0;0) = 2∙02 + 30 + 4 + 20 + F1(3) =4+40 =44
2(1;0) = 2∙12 + 31 + 4 +20 + F1(2)=9+24 =33
2(2;0) = 2∙22 +32 + 4 + 20 +F1(1) =18+12=30*
2(3;0) = 2∙32 + 33 + 4 + 20 + F1(0) =31+4 =35
|
|
y3 = 1
|
0 x2 4
|
x2 = 0
x2 = 1
x2 = 2
x2 = 3
х2 = 4
|
y2 = 4 - 0 = 4
y2 = 4 - 1 = 3
y2 = 4 - 2 = 2
y2 = 4 - 3 = 1
y2 = 4 - 4 = 0
|
2(0;1) = 2∙02 + 30 + 4 + 21 + F1(4) = 6+60=66
2(1;1) = 2∙12 + 31 + 4 + 21 + F1(3) =11+40 =51
2(2;1) = 2∙22 + 32 + 4 + 21 + F1(2)=20+24 =44*
2(3;1) = 2∙32 + 33 + 4 + 21 + F1(1)=33+12 =45
2(4;1) = 2∙42 + 34 + 4 + 21 + F1(0) = 50+4=54
|
|
y3 = 2
|
.......................
|
........
|
............................
|
.............................................................
|
|
y3 = 3
|
0 x2 6
|
x2 = 0
x2 = 1
x2 = 2
x2 = 3
x2 = 4
x2 = 5
х2 = 6
|
y2 = 6 - 0 = 6
y2 = 6 - 1 = 5
y2 = 6 - 2 = 4
y2 = 6 - 3 = 3
y2 = 6 - 4 = 2
y2 = 6 - 5 = 1
y2 = 6 - 6 = 0
|
2(0;3) = 2∙02 + 30 + 4 + 23 + F1(6) = 10+112=122
2(1;3) = 2∙12 + 31 + 4 + 23 + F1(5) =15+84 =99
2(2;3) = 2∙22 + 32 + 4 + 23 + F1(4)=24+60 =84
2(3;3) = 2∙32 + 33 + 4 + 23 + F1(3)=37+40 =77*
2(4;3) =2∙ 42 + 34 + 4 + 23 + F1(2)=54+24 =78
2(5;3) =2∙ 52 + 35 + 4 + 23 + F1(1)=75+12 =87
2(0;3) = 2∙62 + 36 + 4 + 23 + F1(0) = 100+4=104
|
K=3
Таблица 16.
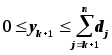
|
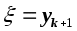
|
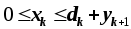
|
xk
|
yk = yk+1 + dk - xk
|
k(xk, yk+1) = k(xk) + hkyk+1 + Fk-1(yk)
|
0 y4 0
|
= y4
|
0 x3 d3 + y4
|
x3
|
y3 = y4 + d3 - x3
|
3(x3, y4) = a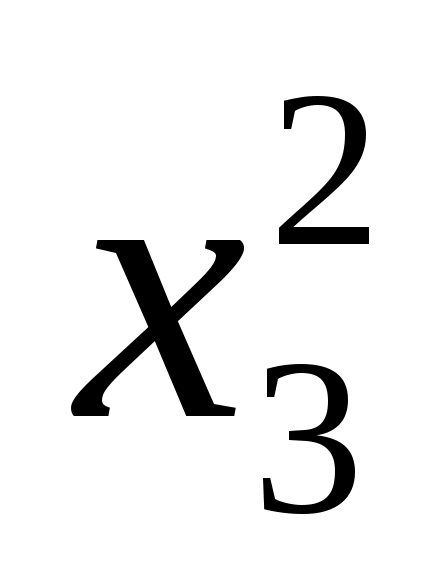 + bx3 + c + h3y4 + F2(y3) + bx3 + c + h3y4 + F2(y3)
|
y4 = 0
|
= y4
|
0 x3 3
|
x3
|
y3 = y4 + 3 - x3
|
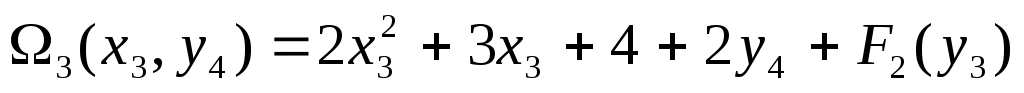
|
|
y4 = 0
|
0 x3 3
|
x3 = 0
x3 = 1
x3 = 2
x3 = 3
|
y3 = 3 - 0 = 3
y3 = 3 - 1 = 2
y3 = 3 - 2 = 1
y3 = 3 - 3 = 0
|
3(0;0) = 2∙02 + 30 + 4 + 20 + F2(3)=4+77=81
3(1;0) = 2∙12 + 31 + 4 + 20 + F2(2)=9+59=68
3(2;0) = 2∙22 + 32 + 4 + 20 + F2(1)=18+44=62
3(3;0) = 2∙32 + 33 + 4 + 20 + F2(0)=31+30=61*
|
Самопроверка результатов Таблица 17.
Этапы
|
январь
|
февраль
|
март
|
Итого за 3 месяца
|
Имеем продукции к началу месяца, шт.
|
у1 = 2
|
у2 = 1
|
у3 = 0
|
у1 = 2
|
Производим в течение месяца, шт.
|
х1 = 1
|
х2 = 2
|
х3 = 3
|
х1+ х2+ х3 = 6
|
Отпускаем заказчикам, шт.
|
d1 = 2
|
d2 = 3
|
d3 = 3
|
d1+ d2+ d3 = 8
|
Остаток к концу месяца (храним в течение текущего месяца), шт.
|
у2 = 1
|
у3 = 0
|
у4 = 0
|
|
Затраты на производство, руб.
|
(х1)=9
|
(х2)=18
|
(х3)=31
|
(х1) + (х2) + (х3) = 58
|
Затраты на хранение, руб.
|
h1у2 = 3
|
h2у3 = 0
|
0
|
h1у2 + h2у3 = 3
|
|
 Скачать 439 Kb.
Скачать 439 Kb.