Прикладная математика. Задача 1 (Линейная производственная задача) Задача 2 Двойственная задача

• Название: Задача 1 (Линейная производственная задача) Задача 2 Двойственная задача
• Дата: 09.06.2022
• Размер: 439 Kb.
• Имя файла: Прикладная математика.doc
• Тип: Задача; #580537
• страница: 2 из 3

Т аблица 7.

	 - x2	0 100 200 300 400 500 600 700
x2	F1( - x2) f2(x2)	0 42 58 71 80 89 95 100
0	0	0 42* 58 71 80 89 95 100
100	30	30 72* 88 101 110 119 125
200	49	49 91* 107* 120 129 138
300	63	63 105 121* 134* 143*
400	68	68 110 126 139
500	69	69 111 127
600	65	65 107
700	60	60 .

Таблица 8.

	0 100 200 300 400 500 600 700
F2()	0 42 72 91 107 121 134 143
 ()	0 0 100 200 200 300 300 300

Таблица 9.

	 - x3	0 100 200 300 400 500 600 700
x3	F2( - x3) f3(x3)	0 42 72 91 107 121 134 143
0	0	0 42* 72* 91 107 121 134 143
100	22	22 64 94* 113* 129* 143 156
200	37	37 79 109 128 144* 158*
300	49	49 91 121 140 156
400	59	59 101 131 150
500	68	68 110 140
600	76	76 118
700	82	82 .

Таблица 10.

	0 100 200 300 400 500 600 700
F3()	0 42 72 94 113 129 144 158
()	0 0 0 100 100 100 200 200

Таблица 11.

	 - x4	0 100 200 300 400 500 600 700
x4	F3( - x4) f4(x4)	0 42 72 94 113 129 144 158
0	0	158
100	50	194
200	68	197*
300	82	195
400	92	186
500	100	172
600	107	149
700	112	112 .

Проверим выполнение равенства

f₁(x*₁) + f₂(x*₂) + f₃(x*₃) + f₄(x*₄) = z _max
58 + 49 + 22 + 68 = 197

Равенство выполняется.

Задача №5.
Динамическая задача управления производством

и запасами
Рассмотрим трехэтапную систему управления запасами с дискретной продукцией и динамическим детерминированным спросом.

Пусть спрос (заявки) потребителей на нашу продукцию составляют: на первый этап d₁=2 единицы, на второй – d₂=3, на третий - d₃=3 единицы. К началу первого этапа на складе имеется только 2 единицы продукции, т.е. начальный уровень запаса равен y₁=2. Затраты на хранение единицы продукции на разных этапах различны и составляют соответственно h₁=3, h₂=2, h₃=2. Затраты на производство x_j единиц продукции на j-м этапе определяются функцией
_j(x_j) =2x_j² + 3x_j + 4 (1)

т.е. а=2; b=3; с=4. Требуется указать, сколько единиц продукции на отдельных этапах следует производить, чтобы заявки потребителей были удовлетворены, а наши общие затраты на производство и хранение за все три этапа были наименьшими.
Решение.
Представим исходные данные задачи в виде таблицы:
Таблица 12.

Период К	1 2 3
Спрос dK, ед	2 3 3
Затраты на производство АК , руб.	2 3 4
Затраты на хранение hK , руб.	3 2 2

Воспользовавшись рекуррентными соотношениями, последовательно вычисляем

F₁ ( = y₂), F₂ ( = y₃), F₃ ( = y₄), и соответственно находим ₁ (= y₂),

₂ ( = y₃ ), ₃ ( = y₄)

Положим k = 1. Тогда имеем
(2)
Учтем, что параметр состояния  = у₂ может принимать целые значения на отрезке

0 у₂ d₂ + d₃ (3)

0 y₂ 3 + 3

т.е.

у₂ = 0, 1, 2, 3, 4, 5, 6.

При этом каждому значению параметра состояния должна отвечать определенная область изменения переменной x₁, а именно

0 х₁ 2 + у₂ (4)
На первом этапе спрос d₁ = 2, исходный запас у₁ = 2. Из балансового уравнения

х₁ + у₁ - d₁ = у₂ (5)

непосредственно следует, что объем производства связан со значением параметра состояния = у₂ соотношением

x₁ = y₂ + d₁ - y₁ = y₂ + 2 - 2 = y₂ (6)
Если задан уровень запаса к началу первого этапа, то каждому значению у₂ отвечает единственное значение х₁ и потому

F₁( = y₂) = ₁ (x₁, y₂) = ах₁² + bx₁ + c + h₁y₂ (7)

Придавая у₂ различные целые значения от 0 до 6 и учитывая (6), находим

y₂ = 0, x₁ = 0, ₁ (0;0) = 2 ∙ 0² + 3  0 + 4 + 3  0 = 4

y₂ = 1, x₁ = 1, ₁ (1;1) = 2 ∙ 1² + 3  1 + 4 + 3  1 = 12

y₂ = 2, x₁ = 2, ₁ (2;2) = 2 ∙ 2² + 3 ∙ 2 + 4 + 3 ∙ 2 = 24

y₂ = 3, x₁ = 3, ₁ (3;3) = 2 ∙ 3² + 3 ∙ 3 + 4 + 3 ∙ 3 = 40

y₂ = 4, x₁ = 4, ₁ (4;4) = 2 ∙ 4² + 3 ∙ 4 + 4 + 3 ∙ 4 = 60

y₂ = 5, x₁ = 5, ₁ (5;5) = 2 ∙ 5² + 3 ∙ 5 + 4 + 3 ∙ 5 = 84

y₂ = 6, x₁ = 6, ₁ (6;6) = 2 ∙ 6² + 3 ∙ 6 + 4 + 3 ∙ 6 = 112

Значения функции состояния F₁( ) представлены в табл. 13.
Таблица 13.

 = y2	0	1	2	3	4	5	6
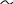F1 ( = y2)	4	12	24	40	60	84	112
x1(=y2)	0	1	2	3	4	5	6

Переходим ко второму этапу. Полагаем k = 2 и табулируем функцию

F₂( = y₃).
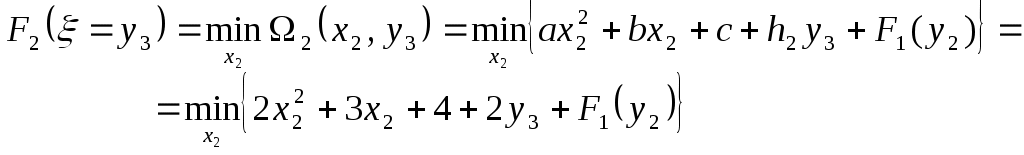(8)
Здесь минимум берется по единственной переменной х₂, которая может изменяться в пределах
0  x₂  d₂ + y₃ или 0  x₂  3 + y₃ (9)
где верхняя граница зависит от параметра состояния  = у₃, который, принимает значения на отрезке
0  y₃  d₃ , т.е. 0  y₃  3 (10)
а аргумент у₂ в последнем слагаемом справа в соотношении (8) связан с х₂ и у₃ балансовым уравнением

x₂ + y₂ - d₂ = y₃

откуда следует

y₂ = y₃ + d₂ - x₂ = y₃ + 3 - x₂ (11)
Придавая параметру состояния различные значения от 0 до 3, будем последовательно вычислять ₂ (x₂, ), а затем определять F₂( ) и ₂( ).

Положим, например  = у₃ = 2. Тогда, согласно (9),

0  x₂  5,
т.е. переменная х₂ может принимать значения: 0, 1, 2, 3, 4, 5, а каждому значению х₂ отвечает определенное значение у₂, вычисляемое по формуле (11):

у₂ = 5 - х₂

Последовательно находим:

если x₂ = 0, то y₂ = 5-0 = 5, ₂ (0,2) = 2∙0² + 30 + 4 + 22 + F₁(5) = 8 + 84 = 92,

x₂ = 1, y₂ = 5-1 = 4, ₂ (1,2) =2∙1² + 31+ 4 + 22 + F₁(4) = 13 + 60 = 73,

x₂ = 2, y₂ = 5-2 = 3, ₂ (2,2) =2∙2² +32 + 4 + 22 + F₁(3) = 22 + 40 = 62,

x₂ = 3, y₂ = 5-3 = 2, ₂ (3,2) =2∙3²+33 + 4 + 22 + F₁(2) = 35 + 24 = 59*,

x₂ = 4, y₂ = 5-4 = 1, ₂ (4,2) = 2∙4² + 34 + 4 + 22 + F₁(1) = 52+12 = 64,

x₂ = 5, y₂ = 5-5 = 0, ₂ (5,2) =2∙ 5² + 35 + 4 + 22 + F₁(0) = 73 + 4 =77 .
Наименьшее из полученных значений ₂ есть F₂ (2), т.е.
F₂ ( = y₃ = 2) = min ₂ (x₂,2) = min (92, 73, 62, 59, 64, 77) = 59,

x₂

причем минимум достигается при значении х₂, равном

 ₂ ( = y₃ = 2) = 3

Аналогично для всех остальных значений у₃ = 0, 1, 3.

F₂ ( = y₃ = 0) = 30;  ₂ ( = y₃ = 0) = 2.

F₂ ( = y₃ = 1) = 44;  ₂ ( = y₃ = 1) = 2.

F₂ ( = y₃ = 3) = 77;  ₂ ( = y₃ = 3) = 3.
Процесс табулирования функции F₂ ( = y₃) приведен в табл. 14, а результаты табулирования сведены в табл. 15.