Мат. анализ. Практическая работа. Задача 1 Методом изоклин построить интегральные кривые уравнения Решение
 Скачать 286.48 Kb. Скачать 286.48 Kb.
|
|
Задача № 1 Методом изоклин построить интегральные кривые уравнения 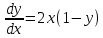 Решение: Найдем уравнение изоклин. По определению уравнение имеет вид 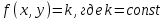 . . Следовательно: 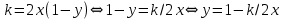 Изоклины представляют собой семейство гипербол. При 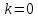 имеем имеем 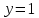 и и 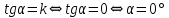 При 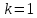 имеем имеем 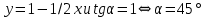 При 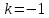 имеем имеем 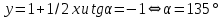 При 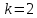 имеем имеем 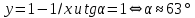 При 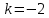 имеем имеем 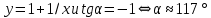 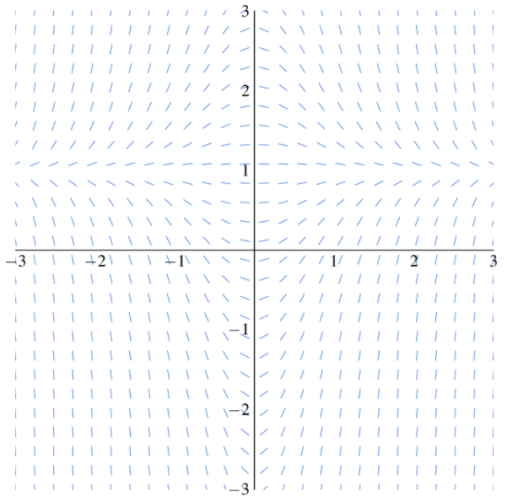 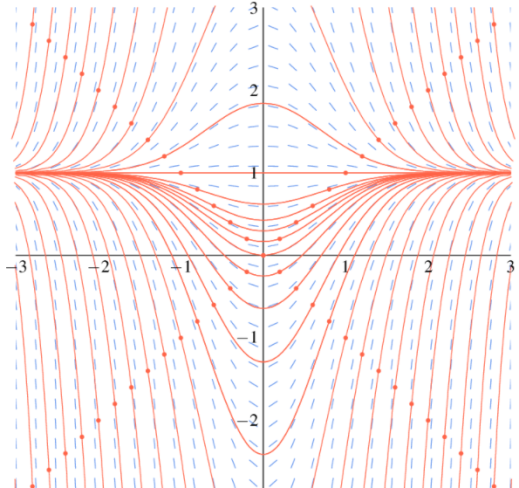 Задача № 2 Решить уравнение, допускающее понижения порядка 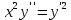 Уравнение вида 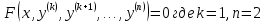 Понижаем порядок уравнения заменой 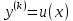 Вычисляем: 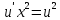 Делим на 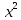 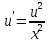 Преобразование 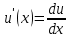 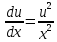 Умножаем на дифференциал 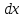 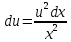 Делим на 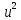 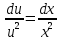 Уравнение с разделяющимися переменными 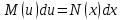 Интегрируем обе части уравнения 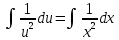 Вычисляем полученные интегралы 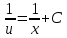 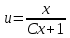 Обратная замена 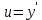 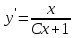 Преобразование 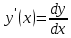 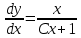 Умножаем на дифференциал 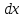 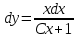 Уравнение с разделяющимися переменными 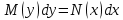 Интегрируем обе части уравнения 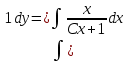 Вычисляем полученные интегралы 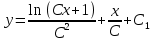 Задача № 3 Решить систему уравнений 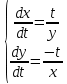 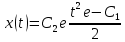 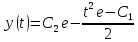 Задача № 4 Пусть производится n опытов, вероятность наступления события A в каждом из которых одинакова, равна p, в задаче это 0,7. Тогда наивероятнейшее число m = 10 наступлений события A в этой серии опытов можно найти по формуле: 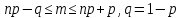 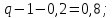 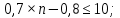 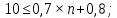 Ответ: можно провести от 14 до 15 испытаний. |
