Розрахунково-проектна робота. Задача 1 На рисунку показано ступінчатий стержень. Матеріал стержня низьковуглецева сталь. Допустиме напруження 160
 Скачать 0.86 Mb. Скачать 0.86 Mb.
|
|
2) Знаходимо положення головних площин : 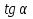 = = 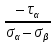 = = 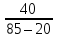 = 0.6; = 0.6;α = arctg ( 0.6 ) = 30̊ 9 '. 3) Визначаємо максимальні дотичні напруження : τmax = 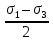 = 52.5 МПа. = 52.5 МПа.4) Вираховуємо величини повних відносних деформацій : Ɛ1 = 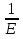 (σ1 – µ( σ2 +σ3)) = (σ1 – µ( σ2 +σ3)) = 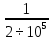 ( 104 · 106 – 0.28 ( 30 · 106 + 1· 106) ) = 476.6; ( 104 · 106 – 0.28 ( 30 · 106 + 1· 106) ) = 476.6;Ɛ2 = 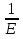 (σ2 – µ( σ1 +σ3)) = (σ2 – µ( σ1 +σ3)) = 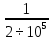 ( 30 · 106 – 0.28 ( 104 · 106 + 1· 106) ) = 3; ( 30 · 106 – 0.28 ( 104 · 106 + 1· 106) ) = 3;Ɛ3 = 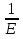 (σ3 – µ( σ2 +σ1)) = (σ3 – µ( σ2 +σ1)) = 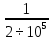 ( 1 · 106 – 0.28 ( 30 · 106 + 104· 106) ) = – 182.6. ( 1 · 106 – 0.28 ( 30 · 106 + 104· 106) ) = – 182.6.Зміну об’єму можна вирахувати наступним шляхом : ƐV = Ɛ1 +Ɛ2 +Ɛ3 ƐV= 476.6 + 3– 182.6 = 297; 5) Визначимо питому енергію деформацію : Вона складається з питомої потенціальної енергії зміни об’єму Uvта питомої потенціальної енергії зміни форми деформації Uф U = Uv + UФ Uv= 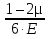 (σ1 + σ2 + σ3) 2 = (σ1 + σ2 + σ3) 2 = 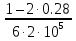 ( 104 +30 + 1 )2 = 0.0061 Дж / м3 ; ( 104 +30 + 1 )2 = 0.0061 Дж / м3 ;UФ = 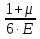 ( σ1 + σ2) 2 + ( σ2 + σ3) 2 + ( σ3 + σ1) 2 = ( σ1 + σ2) 2 + ( σ2 + σ3) 2 + ( σ3 + σ1) 2 = 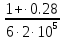 (104 + 30)2 + (104 + 30)2 + + (30 + 1)2 + (1 + 104 )2 = 0.0137 Дж / м3 ; U = Uv + UФ = 0.0061 + 0.0137 = 0.0198 Дж / м3. 6) Робимо перевірку на міцність : Сталь Ст.3 – [σ] = 160 МПа, σТ = 230 МПа. σекв1 = σ1 – σ3 = 104 – 1 = 103 МПа; σекв1 < [σ] < σТ σекв2 = 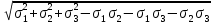 = 91,99 МПа; = 91,99 МПа;σекв2 < [σ] < σТ МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ Національний авіаційний університет Кафедра механіки РОЗРАХУНКОВО-ПРОЕКТНА РОБОТА № 2 Геометричні характеристики плоских перерізів. Плоске згинання. Кручення Факультет Літальних апаратів Група 211 Студент Кожедуб Сергій Олексійович Варіант 8 Оцінка____________________ «____»____________20____ р. Викладач Астанін В’ячеслав Валентинович Київ 2017 р. Задача 4 Для складного перерізу потрібно визначити величини головних центральних моментів інерції і положення головних центральних моментів інерції і положення головних центральних осей. Дані для розрахунку: Складний переріз має наступний вигляд: 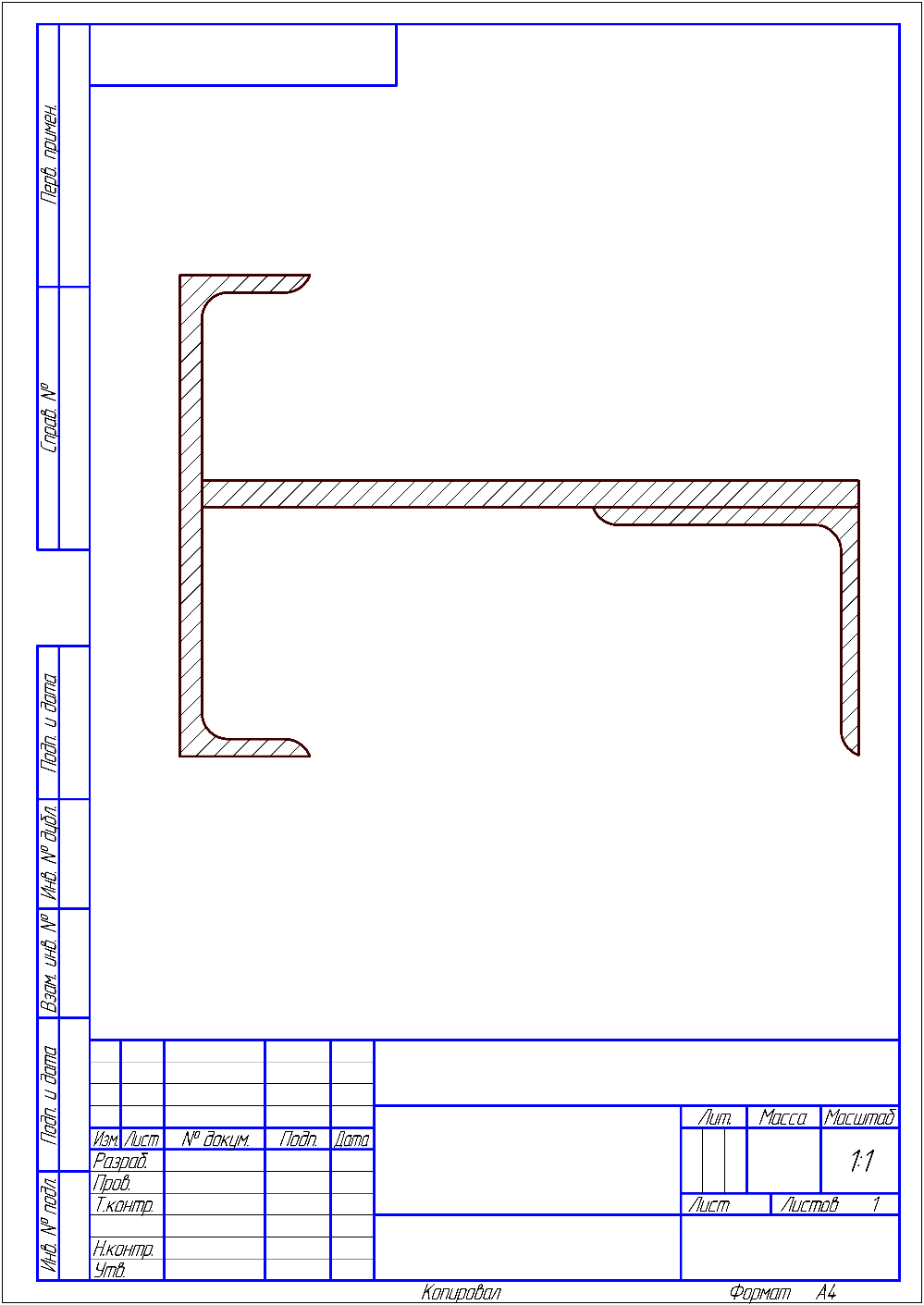 Згідно сортименту прокатної сталі елементи перерізу мають наступні характеристики: Швелер (ГОСТ 8240 – 89) №30 h= 30 см Jz = 5810 см4 b=10 см Jy= 327 см4 s =0,65 см A=40.5 см2 t=1.1 см z0 = 2.52 см Кутик (ГОСТ 8509 – 72)№ 14 B = 14 см Jz = 444.45 см4 b = 9 см Jy = 145.54 см4 t=1 см x0 = 2.12 см A = 22.24 см2y0 = 4.58 см Лист b= 39 см A= 54.6 см2 h = 1.4 см Розв’язання 1) Накреслимо переріз в масштабі, поставивши розміри. 2) Визначаємо площу складного перерізу: А = А1 + А2 + А3 = 40.5 + 27.3 +54.6 = 122.4 см2 Вибираємо початкові взаємно перпендикулярні координати осі Z та Y визначаємо відносно них статистичні моменти перерізу Sy і Sz Sy1 = A1 · z1 ; z1 = zoшв = 2.52 = 2.52 см ; Sy1 = 40.5 · 2.52 = 102.06 см 3; Sy2 = A2 · z2 ; z2 = 0.5 · bлист = 0.5 · 39 = 19.5 см 3 ; Sy2= 54.6 · 19.5 = 1064.7 см 3 ; Sy3 = A3 · z3 ; z3 = sшв + bлиста – x0 кутика = 37.53 см ; Sy3 = 27.3 · 37.53 = 1024.569 см 3 ; Sz1 = A1 · y1 ; y1 = 0 см ; Sz1 = 0 ; Sz2 = A2 · y2 ; y2 = 0 см ; Sz2= 0 ; Sz3 = A3 · y3 ; y3 = – y0 кутика= – 4.58 см ; Sz3 = 27.3 · ( – 4.58 ) = – 101.8592 см 3; 3) Визначаємо положення центра ваги перерізу : 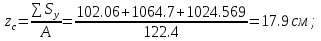 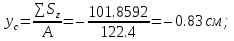 4) Визначаємо відносно центральних осей 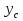 та та 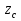 осьові Jyc, Jzc та відцентровий Jyczc моменти інерції : осьові Jyc, Jzc та відцентровий Jyczc моменти інерції :Осьові моменти кожного перерізу відносно центральної осі OZ обчислюються за правилами знаходження моменту інерції відносно паралельних осей : Jzc = Jz + a2 · A де Jzc - шуканий момент інерції відносно центральної осі OZ складного перерізу, Jz- момент інерції перерізу відносно осі, що проходить через центр його ваги паралельно до центральної осі OZ , a - відстань по осі OY від центральної осі OZ до осі перерізу, що проходить через центр його ваги паралельно до центральної осі OZ (знак мінус ставиться тоді, коли центр ваги фігури лежить під центральною віссю або за нею) , A - площа поперечного перерізу. Jzc1 = Jz1 + a12 · A1 a1 = zc – z0 швелера = 15.38 см ; Jzc1= 5810 + ( 15.38 ) 2 · 40.5 = 15390.0482 см 4 ; Jzc2 = Jz2 + a22 · A2 a2 = 0.5 bлиста – zc = 1.6см ; 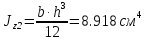 Jzc2 = 8.918 + ( 1.6 ) 2 · 54.6 = 148.694 см4 ; Jzc3 = Jz3 + a32 · A3 a3 = dлиста + х0 кутика – ( zс – sшвелера ) = 19.63 см ; Jzc3 = 445.45 + 19.63 2 · 22.4 = 9014.34 см4 . Загальний момент інерції вираховується як сума моментів інерції кожного елемента відносно одного напрямку осі : Jzc = Jzc1 + Jzc2 + Jzc3 = 15390.0482 + 148.694 + 9014.34 = 24553.0822 см4 Знаходимо осьові моменти інерції відносно осі OY : Jyc = Jy + b2·A де Jyc - шуканий момент інерції відносно центральної осі OY складного перерізу, Jy- момент інерції перерізу відносно осі, що проходить через центр його ваги паралельно до центральної осі OY , b- відстань по осі OZ від центральної осі OY до осі перерізу, що проходить через центр його ваги паралельно до центральної осі OY (знак мінус ставиться тоді, коли центр ваги фігури лежить під центральною віссю або за нею) , A - площа поперечного перерізу. Jyc1 = Jy1 + b12 · A1 b1 = 0 ; Jyc1= 327 см 4 ; Jyc2 = Jy2 + b22 · A2b2 = 0 ; 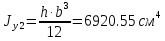 Jyc2 = 6920.55 см4 ; Jyc3 = Jy3 + b32 · A3 b3 = – y0 кутика = – 4.58 см ; Jyc3 = 145.54 + ( – 4.48 ) 2 · 22.24 = 612.055 см4 . Jyc = Jyc1 + Jyc2 + Jyc3 = 327 + 6920.55 + 612.055 = 7859.605 см4. Обчислюємо відцентрові моменти інерції кожного перерізу. Для цього використаємо наступну формулу : Jyczc = Jyz + a·b·A тут Jyczc - відцентровий момент інерції перерізу відносно центральних осей, Jyz - момент інерції перерізу відносно осей, що проходять через його центр ваги J1yczc = Jy1z1 + a1 · b1 · A1 = a1 · b1 · A1 = 0 ; J 2yczc = Jy2z2 + a2 · b2 · A2 = a2 · b2 · A2= 0 ; J 3yczc= Jy3z3 + a3 · b3 · A3 = a3 · b3 · A3 = 4.87 · 7.15 · 54.6 = –1999.47см4 ; Jyczc= J1yczc+ J2yczc+ J3yczc= – 1999.47 см4 . 5) Визначаємо положення головних центральних осей інерції Y0 та X0 : 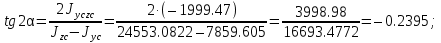 2α = arctg ( – 0.2395 ) = – 13 ̊ 46 ʹ ; α = – 6 ̊ 73ʹ . Положення головних центральних осей UV задається повертанням центральних осей на заданий кут. Знайдений кут повинен бути між віссю U і центральною віссю, відносно якої момент інерції складного перерізу найбільший (знайдений кут дуже малий, тому на малюнку можна показати його трохи збільшеним). |
