Розрахунково-проектна робота. Задача 1 На рисунку показано ступінчатий стержень. Матеріал стержня низьковуглецева сталь. Допустиме напруження 160
 Скачать 0.86 Mb.
|
|
6) Підрахуємо величини головних центральних моментів інерції Jyo та Jzo : 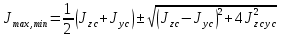 Jmax = Ju = 33372.12 см 4Jmin = Jv = –959.4364 см 4 24553.0822 + 7859.605 = 33372.12 – 959.4364 32412.68 = 32412.68 7) Визначаємо величини головних радіусів інерції та показуємо на малюнку центральний еліпс інерції : 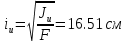 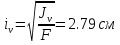 Радіуси відкладаються вздовж головних центральних осей, при чому iu відкладається вздовж осі V, а iv вздовж осі U. Задача 5 На малюнку показано чотири балки. Допустиме напруження [σ] = 160 МПа. Потрібно: 1) для чотирьох балок побудувати епюри поперечних силQ і згинальних моментів M. 2) Для однієї з балок: · підібрати двотавровий переріз; · перевірити міцність балки за найбільшими нормальними та дотичними напруженнями . Дані для розрахунку: F = 16 кН,M = 22 кН · м, q = 28 кН/м, a = 1,4 см. Для консольних балок потрібно прийняти a = а/4 = 0,0035 м. Розв’язання 1) Дослідження балок: Розрахунок балки проводиться в наступному порядку: · визначаємо реакції опору та, якщо є жорстка забудова, її момент опору; · потім робимо розрахунок кожної ділянки окремо; Складаємо рівність для знаходження реакцій опор першої балки враховуючи те, що сума зовнішніх сил і реакцій, що діють на балку дорівнюють нулю : 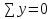 RA – F + F = 0RA = – F + F = 0 Для знаходження моменту жорсткої забудови скористаємося тим, що сума моментів всіх сил, діючих на систему відносно одного певного центру дорівнює нулю, коли тіло знаходиться у стані рівноваги. 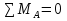 – F · a + F· 2a – M + MA = 0МА = F · a – F· 2a + M= 21.944 кН · м Далі розглядаємо кожну ділянку по черзі, починаючи з початку балки, всі ділянки пронумеровані з ліва на право, осі координат знаходяться на лівому кінці всіх балок. В розрахунок ділянки входить знаходження поперечних сил та моментів, які діють вздовж всієї ділянки. Поперечна сила, яка діє на ділянку визначається сумою всіх поперечних сил, що прикладені на попередніх ділянках і на межі, де починається дана ділянка. Це означає, що поперечна сила зміниться тільки на тій межі ділянок, де буде прикладене зосереджене навантаження. Якщо ж на межі ділянки прикладене розподілене навантаження, то сумарна сила, що діє на балці змінюється плавно. Аналогічно виконується обчислення моментів. Момент не змінюється до тих пір, поки на межі якої небудь ділянки не будуть прикладені ні моменті, ні сили. Якщо на межі ділянок зустрічається момент, то сумарний момент змінюється різко. Коли з’являється сила, то момент починає плавно змінюватися після точки прикладання цієї сили, бо при віддаленні від цієї точки збільшується плече моменту і він відповідно зростає і впливає на сумарний момент тим більше, чим більша відстань від точки прикладення сили. Момент розподіленого навантаження змінюється по квадратичному закону, бо разом із збільшенням плеча, зростає і сумарна сила, тому для побудови схеми слід вираховувати значення моменту ще й у центрі ділянки, яка містить такий вид навантаження. Щоб перевірити правильність побудови епюр, треба щоб виконувалися наступні умови: · В першій ділянці поперечна сила дорівнює навантаженню, що стоїть на початку цієї ділянки (реакція опори). · Сила на останній ділянці дорівнює силі, прикладеній в кінці цієї ділянки. · Для моментів виконуються ті самі умови, що і для сил. · Епюра сили різко стрибає тільки там, де прикладене зосереджене навантаження, а момент тільки там, де прикладений момент. Балка №1 ( балка консольна тому a = а/4 = 0,0035 м ) 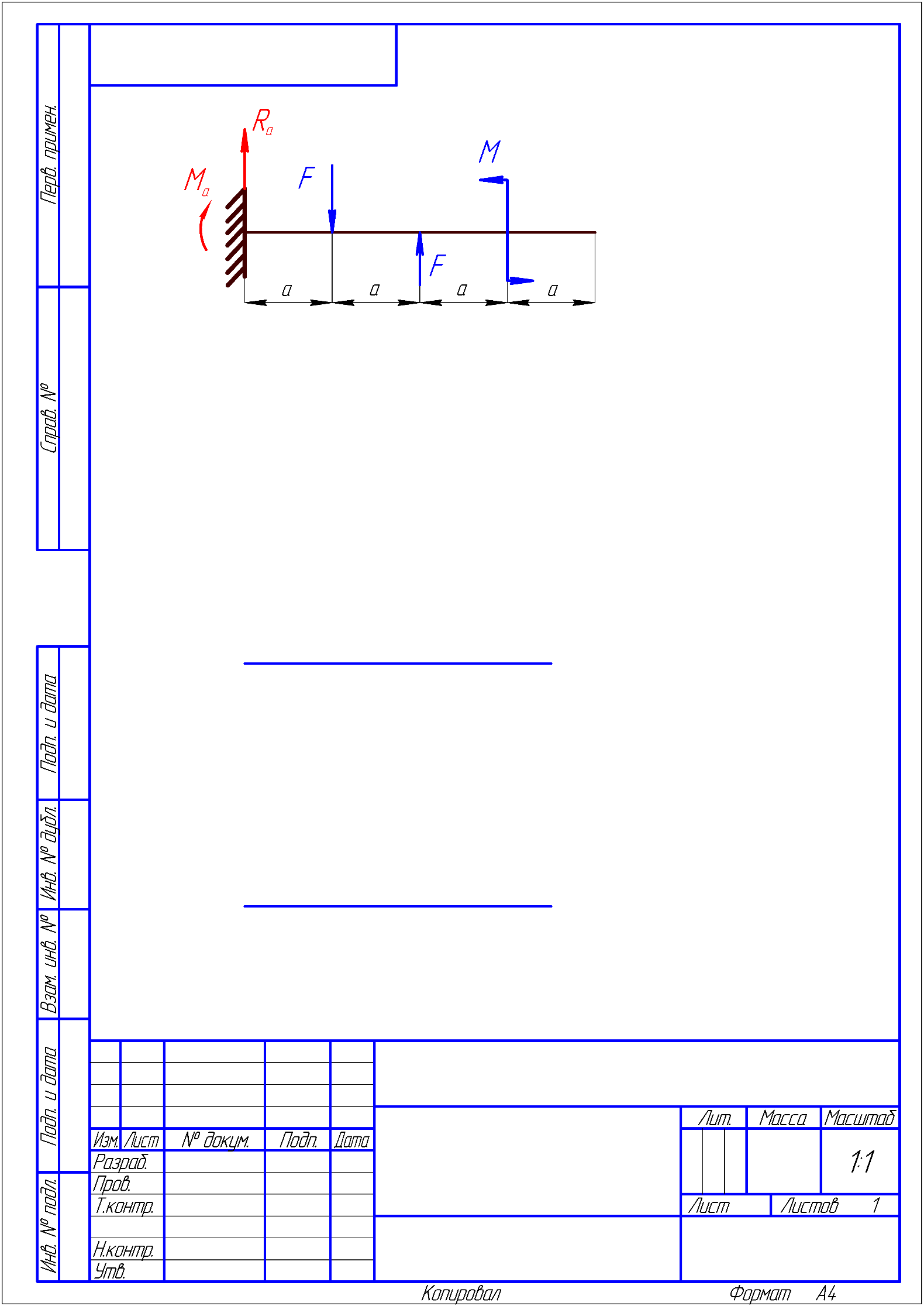 Знайдемо реакцію жорсткої забудови : 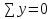RA – F + F = 0RA = – F + F = 0 Тепер знайдемо момент в забудові : 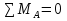– F · a + F· 2a – M + MA = 0МА = F · a – F· 2a + M= 21.944 кН · м Напрямок МА вибрано правильно. Ділянка І 0 ≤ x1 ≤ a при х = 0 Q1 = R A = 0M1 =MA + RA · a= 21.944 кН · м при х = аQ1 = RA= 0M1= MA + RA · a = 21.944 кН · м Ділянка ІІ a ≤ x2 ≤ 2a при х = a Q2 =RA – F= – 16 кН M2 = MA + RA · a – F · ( x – a ) = 21.944кН · м при х = 2а Q2 = RA – F= – 16 кН M2 = MA + RA · a – F · ( x – a ) = 22.056 кН · м Ділянка ІІІ 2a ≤ x3 ≤ 3a при х = 2a Q3 = RA – F + F = 0 M3 = MA + RA · x – F · a + F · 2a = 22.056 кН · м при х = 3а Q3 =0 кН M3= MA + RA · x – F · a + F · 2a = 22.224 кН · м Ділянка IV 3a ≤ x4 ≤ 4a при х = 3aQ4 = RA – F + F = 0 M4 = MA + RA · x – F · a + F · 2a + M = 0.224кН · м при х = 4аQ4 = RA – F + F = 0 M4 = MA + RA · x – F · a + F · 2a + M = 0.224кН · м Балка №2 ( балка консольна тому a = а/4 = 0,0035 м ) 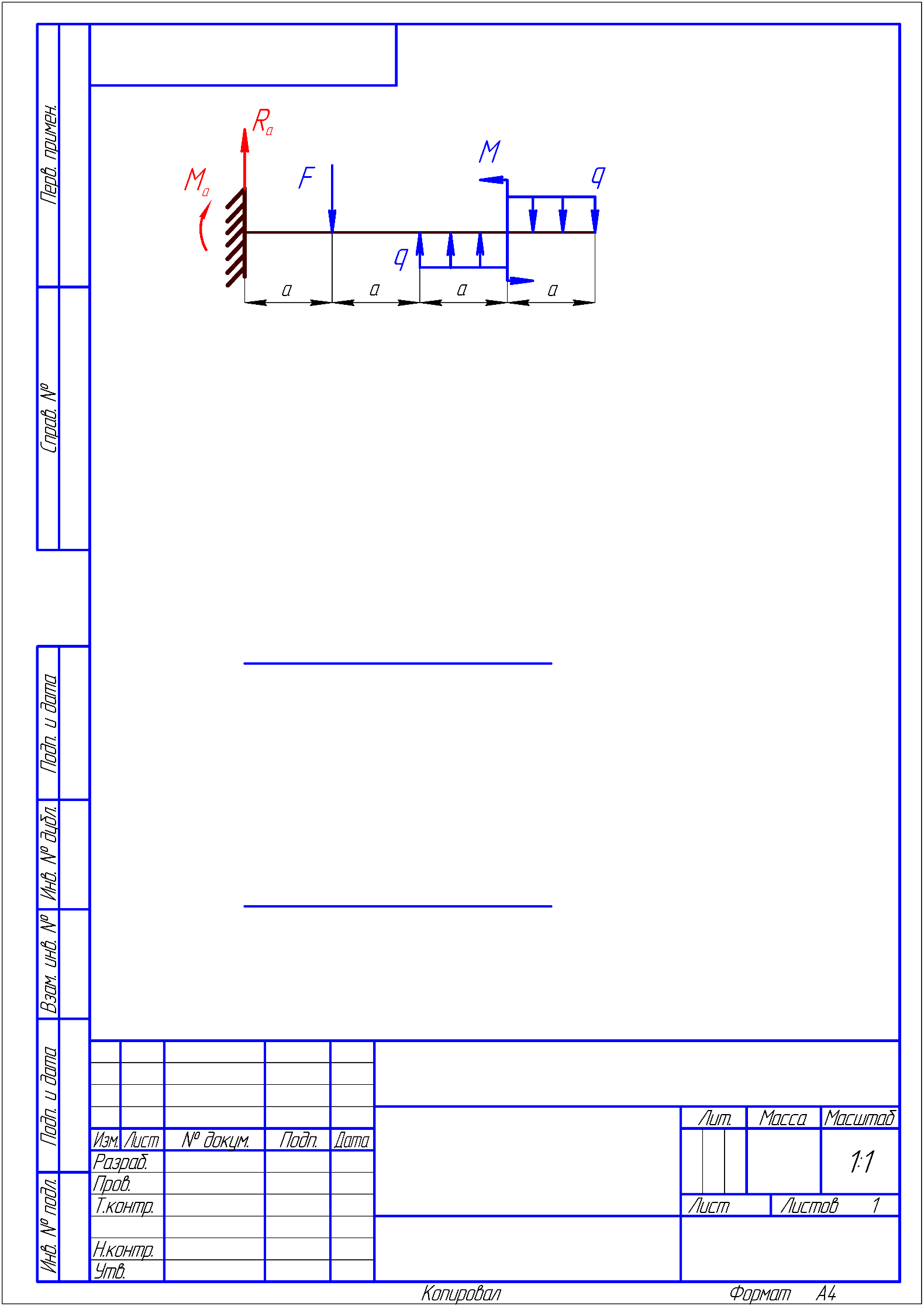 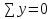RA – F + q · a – q · a = 0RA = F = 16 кН 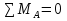MA– F · a + q · a · 2.5 a + q· a · 3.5 a – M = 0 МА = 22.056 кН Напрямок МА вибрано правильно. Ділянка І 0 ≤ x1 ≤ a при х = 0 Q1 = RA – F = 0M1 = MA + RA · x = 22.056 кН · м при х = аQ1 = RA – F = 0M1 = MA + RA · x = 22.112 кН · м Ділянка ІІ a ≤ x2 ≤ 2a Q2 = RA – FM2 = MA + RA · x– F · ( x – a ) при х = a Q2 = RA – F=0M1 = MA + RA · x– F · ( x – a )= 22.112 кН · м при х = 2аQ2 = RA – F=0M1 = MA + RA · x– F · ( x – a )= 22.056 кН · м Ділянка ІІІ 2a ≤ x3 ≤ 3a при х = 2aQ3 = RA – F + q ( x – 2a )=0 M3 = MA + RA · x– F · а + q · ( x – 2а ) · 2.5 а =22.056 кН · м при х = 3аQ3 = RA – F + q ( x – 2a )=0.098 кН M3 = MA + RA · x– F · а + q · ( x – 2а ) · 2.5 а =0.1128 кН · м Ділянка IV 3a ≤ x4 ≤ 4a при х = 3aQ4 = 0.098 кН M4 = – 21.8872 кН · м при х = 4аQ4 = 0 M4 = – 21.832 кН · м Балка №3 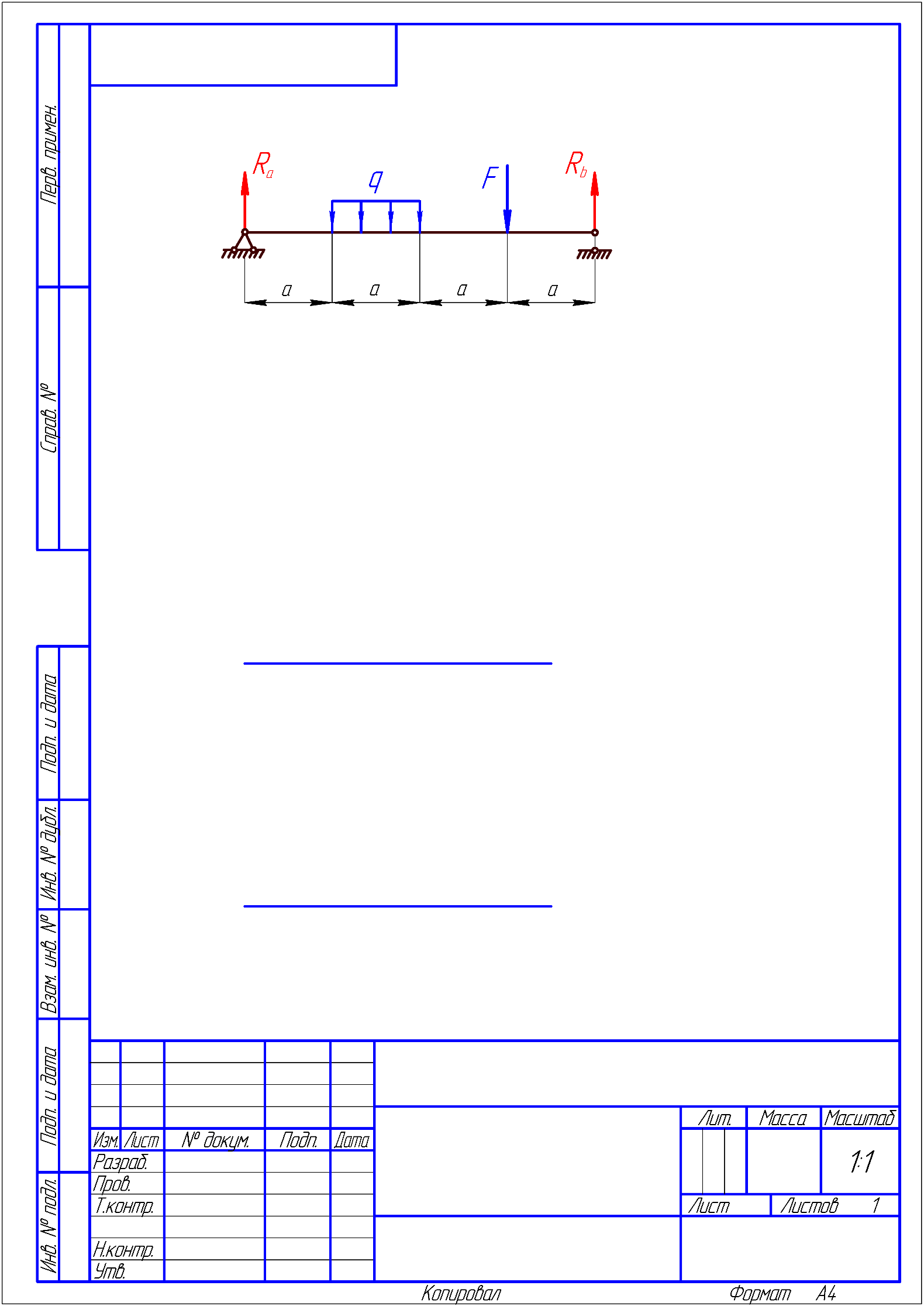 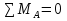RB · 4a – F· 3a – q·a · 1.5a = 0 RB = 12.126 кН 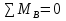 - RA· 4a – q·2.5 a2 + F· a = 0RA = 4.21 кН Ділянка І 0 ≤ x1 ≤ a при х = 0 Q1 =RA = 4.21кН M1 = 0 при х = а Q1 =RA = 4.21кН M1 = RA·a= 0.05052кН · м Ділянка ІІ a ≤ x2 ≤ 2a при х = a Q2 = RA – q · 0= 4.21кН M1 = RA·a – q · 0= 0.05052кН · м при х = 2аQ2 =RA – q · a = 3.874 кН M2 =RA·2 a – ( q · a2 ) / 2 = 0.099024кН · м Ділянка ІІІ 2a ≤ x3 ≤ 3a при х = 2aQ3 = RA – q · a = 3.874 кН M3 = RA·2 a – ( q · a2 ) / 2 = 0.099024кН · м при х = 3аQ3 = RA – q · a = 3.874 кН M3 = RA·3 a – 1.5 q · a2 = 0.145512кН · м Ділянка IV 3a ≤ x4 ≤ 4a при х = 3aQ4 = RA – q · a - F = – 12.126 кН M4 = RA·3 a – 1.5 q · a2 – F · 0 = 0.145512кН · м при х = 4аQ4 = RA – q · a - F = – 12.126 кН M4 = RA·4 a – 2.5 q · a2 – F · a = 0.00144кН · м Балка №4 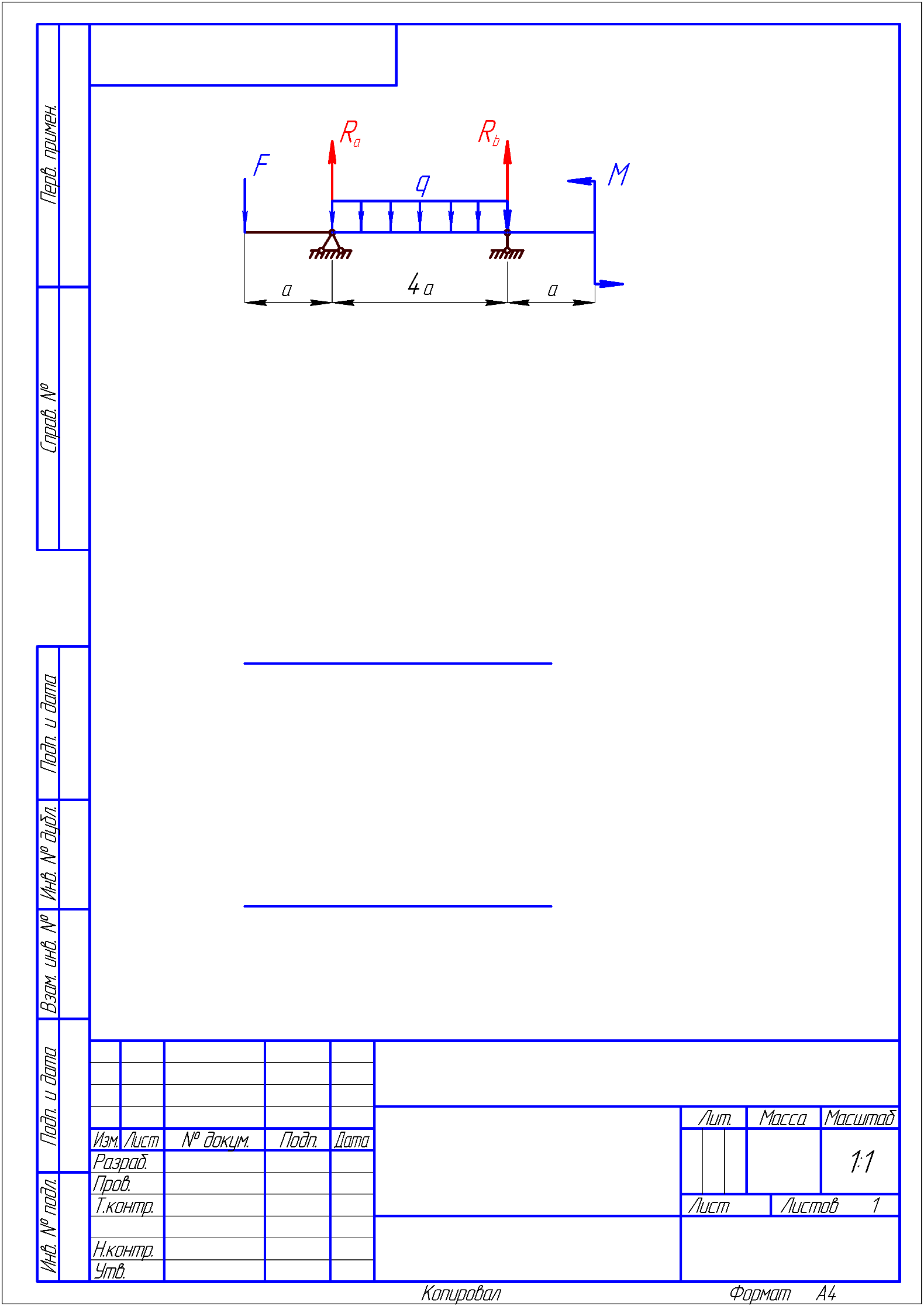 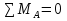– M + RB · 4a – q · 4a2 – F · a = 0 RB = 455.005 кН 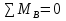– M – RA · 4a – q · 4a2 – F ·5 a = 0 RA = –437.661 кН Ділянка І 0 ≤ x1 ≤ a при х = 0 Q1 = – F = – 16кНM1= – F · a = 0 при х = аQ1 = = – F = – 16кНM1= – F · a = – 0.192кН · м Ділянка ІІ 4a ≤ x2 ≤ 5a при х = 4a Q2 = – F + RA = – 453.661кНM2 =– 0.192кН · м при х = 5аQ2 = – F + RA –q · 4a= – 455.005 кН M2 = – F · 5a + RA · 4a – ( q · a 2 ) / 2 = – 22 кН · м Ділянка ІІІ 5a ≤ x3 ≤ 6а при х = 5aQ3 = – F + RA– q · 4a + RB= 0 M3 =– F · 5a + RA · 4a – 2q · a 2 = – 22 кН · м при х = 6а Q3 =– F + RA– q · 4a + RB= 0 M3= – F · 6a + RA · 5a – 3· q · a 2+ RB · a = – 22 кН · м |