Розрахунково-проектна робота. Задача 1 На рисунку показано ступінчатий стержень. Матеріал стержня низьковуглецева сталь. Допустиме напруження 160
 Скачать 0.86 Mb. Скачать 0.86 Mb.
|
  МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИНаціональний авіаційний університет Кафедра механіки РОЗРАХУНКОВО-ПРОЕКТНА РОБОТА №1 Факультет Літальних апаратів Група 211 Студент Кожедуб Сергій Олексійович Варіант 8 Оцінка____________________ «____»____________20____ р. Викладач Астанін В’ячеслав Валентинович Київ 2017 р. Задача 1 На рисунку показано ступінчатий стержень. Матеріал стержня — низьковуглецева сталь. Допустиме напруження [σ]=160 МПа. Модуль пружності Е = 2·105 МПа. Потрібно:
Дані для розрахунку : Навантаження……………………. F = 32 кН, q = 9,0 кН/м; Довжина.…………………………. a= 16см; Площа……………………………. А = 3,8 см2. Порядок розв’язання задачі
Розв’язання 1) Визначаємо нормальну силу в характерних перерізах стержня. Нехай для нормальної сили напрямок в бік опори буде від’ємним. N1 = F - q1 x1 0 ≤ x1 ≤ 2,5a при x1 = 0 N1= F = 32 кН при x2 = 2a N1 = F-q1 ·2a = 32 – 9,0 ·2·0,16 =29,12кН N2 = N1 N3 = F -q1 ·2a - 3F = 32 - 9,0·2·0,16 - 3·32 = -66,88 кН N4 = N3 N5 = F -q1 ·2a - 3F + F = -34,88 кН 2) Підраховуємо нормальне напруження в необхідних поперечних перерізах:σ 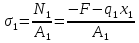 при 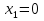 σ1= σ1= 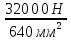 = 50МПа = 50МПа при 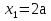 σ1 = σ1 = 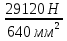 = 45,5МПа = 45,5МПа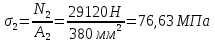 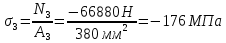 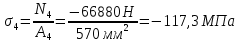 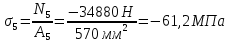 3)Складемо рівняння повздовжніх переміщень на кожній ділянці стержня: Спочатку визначимо абсолютні подовження кожної ділянки. Оскільки стержень залишається нерухомим, то беремо ділянки, починаючи від опори. 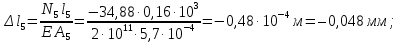 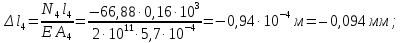 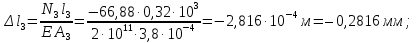 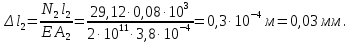 У випадку розподіленого навантаження (ділянка 1) подовження змінюється не за лінійним законом, тому для його обчислення використовуємо інтеграл. Оскільки розглядаємо стержень із права на ліво, то нормальна сила на першій ділянці діятиме за законом N=N2 –qx1 . Для знаходження подовження необхідно проінтегрувати цей вираз. В результаті отримаємо наступний інтеграл: 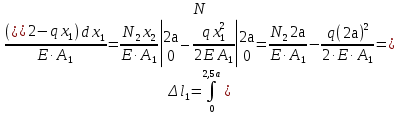 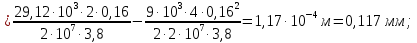 Оскільки на цій ділянці діє розподілене навантаження, подовження всієї ділянки буде змінюватися по параболі, і для зображення його епюри потрібно визначити значення ще й у центрі ділянки. 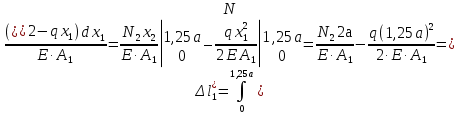 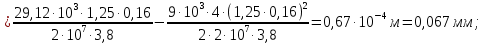 Для побудови переміщень знайдемо переміщення відносно початку стержня, тобто відносно точки з’єднання стержня з поверхнею. Початкове переміщення дорівнює нулю, тому епюра починається з нуля. На межі п’ятої та четвертої ділянки переміщення дорівнює абсолютному подовженню п’ятої ділянки. На межі четвертої і третьої ділянок переміщення дорівнює подовженню четвертої ділянки, але оскільки п’ята ділянка подовжилась, то четверта переміститься ще й на величину подовження п’ятої ділянки, отже переміщення буде дорівнювати сумі подовжень п’ятої і четвертої ділянок. І таким чином визначається переміщення на всіх ділянках. 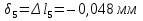 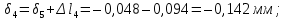 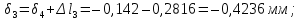 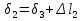 = =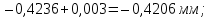 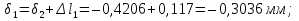 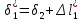 = =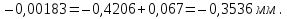 4) Перевіряємо виконання умови міцності на кожній ділянці бруса і обчислюємо допустимі величини площ поперечних перерізів [ 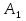 ]: ]:[σ] = 160 МПа; | 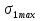 | = 45,5 МПа; [ | = 45,5 МПа; [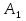 ] = ] = 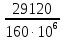 = = 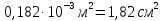 | σ2 |= 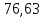 МПа; [ МПа; [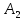 ]= ]= 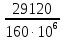 = = 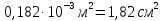 | σ3| = 176 МПа; [ 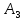 ]= ]= 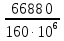 = =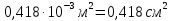 | σ4 |= 117,3 МПа; [ 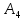 ]= ]= 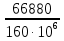 = = 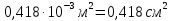 | σ5 |= 61,2 МПа; [ 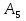 ]= ]= 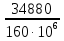 = =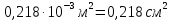 Висновок : Умова міцності виконується на першій, другій, четвертій і п’ятій ділянках бруса. Лише на третій ділянці нормальне напруження більше аніж допустиме, тому на цій ділянці потрібно збільшити площу поперечного перерізу.  Задача 2 На рисунку показано ступінчастий стержень. Матеріал стержня — низьковуглецева сталь. Допустиме напруження [σ] = 160 МПа. Коефіцієнт лінійного розширення α = 1,25 · 10-5. Потрібно: 1) побудувати епюри нормальних сил N, нормальних напружень σ і переміщень поперечних перерізів δ по довжині стержня, якщо стержень виготовлено коротшим заданого розміру на ∆ ; 2) визначити величини напружень в перерізах стержня, якщо він нагрівається на ∆t̊ , вважаючи, що сила F = 0. Дані для розрахунку: Навантаження……………………….. F = 65 кН; Довжина……………………………... a = 57 см; Площа………………………………... A = 8,0 см2; Зазор…………………………………. ∆ = 0,13 мм; Зміна температури………………….. ∆t = 85 град. Розв’язання : 1) Визначаємо RA : -RA– F + 5F = 0; RA = 4F = 260кН. 2) Визначаємо нормальну повздовжню силу, напруження переміщення на кожній ділянці : Ділянка 1: N1 = RA= 260кН; 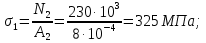 Ділянка 2: N2 = RA+ F= 260 + 65 = 325кН; 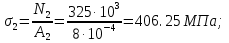 Ділянка 3: N3 = RA + F = 325 кН; 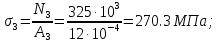 Ділянка 4: N4 = RA+ F – 5F = 260 – 4·65 = 0 кН; 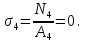 Знаходимо подовження кожної ділянки 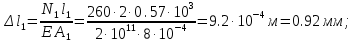 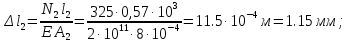 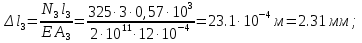 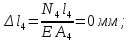 Знаходимо переміщення перерізів 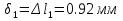 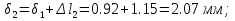 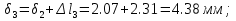 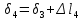 = =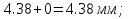 Отже : 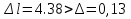 . .При заданих значеннях сили F брус стає статично невизначеним , також при такому значенні сили на другій та на третій ділянках виникає руйнівне навантаження , яке більше за допустиме [σ] = 160 МПа. Тому, щоб запобігти руйнування потрібно збільшити товщину стержня. 3) Обчислимо подовження стержня при зміні температури : ∆lt = α · ∆t · 7a = 1,25 · 10-5 · 85 · 7 · 0,57 = 0,424 · 10 -3 м = 0,424 мм . ∆lt перевищує величину розміру зазору ∆, тому в точці дотику стержня до поверхні виникне реакція RB , яка буде стискати стержень на величину його зайвого подовження, тобто ( 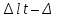 ). ).RA = - RB. В результаті дії реакції стержень має скоротитися на величину ( 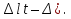 На протязі всього стержня діє тільки реакція RA і тому можна розбивати цей стержень тільки на дві ділянки, межа яких – точка зміни площі поперечного перерізу стержня. Вирахуємо подовження під дією реакції опори: 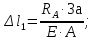 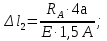 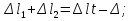 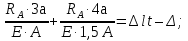 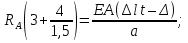 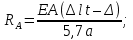 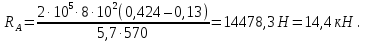 4) Знайдемо температурні напруження на всіх ділянках стержня : Ділянка 1: N1 = RA = 14,4кН; σ1 = N1/А= 18 МПа; Ділянка 2: N2 = RA = 14,4 кН; σ2 = N2 /1,5А = 12 МПа. Висновок: На усіх ділянках напруження задовольняється умова міцності, тобто вони менші ніж максимально допустиме напруження[σ] = 160 МПа. Задача 3 Навколо деякої точки напруженого тіла виділено елемент. Модуль пружності для матеріалу Е=2·105 МПа; коефіцієнт Пуассона µ = 0,28. Потрібно: 1) визначити головні напруження; 2) знайти положення головних площадок та показати лінії дії головних напружень; 3) визначити найбільші дотичні напруження і положення площадок, на яких вони діють; 4) обчислити повні відносні деформації та відносну зміну об’єму; 5) визначити питому потенціальну енергію деформації; 6) провести перевірку міцності матеріалу. Дані для розрахунку: σx = 85 МПа; σy =20 МПа; σz = 30 МПа; τxy =40 МПа. Розв’язання 1) Визначаємо головні напруження: Для цього виконуємо перетворення напружень у відповідності з правилами опору матеріалів та показуємо їх на ортогональній проекції елементу. 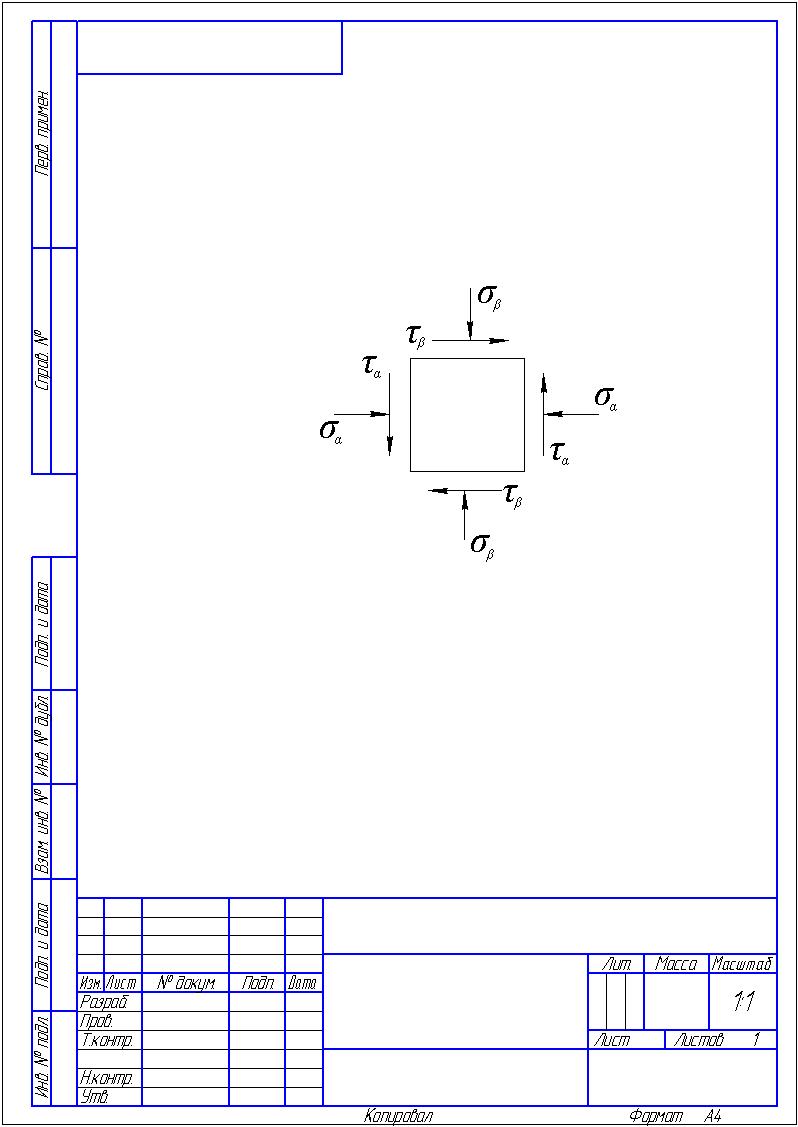 σz = одне з головних по визначенню; σy = – σβ = – 20 МПа; σx = – σα = – 85 МПа; τxy = τβ = 40 МПа; τyx = – τxy = τα= – 40 МПа. Тепер знаходимо величини головних напружень : 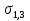 = = 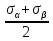 ± ± 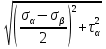 = 52.5 ± 51.5 МПа; = 52.5 ± 51.5 МПа;σ1 = 104 МПа; σ3= 1 МПа; Звідси видно, що σz → σ2 = 30 МПа. Таким чином остаточно маємо: σ1= 104 МПа; σ2=30 МПа; σ3 = 1 МПа . σ1 > σ2 > σ3 |
