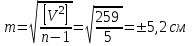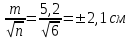ЗАДАЧИ. Задача 1 Найдите квадратическую и относительную погрешность измерений
 Скачать 36.46 Kb. Скачать 36.46 Kb.
|
|
Задача 1.1 Найдите квадратическую и относительную погрешность измерений. Дано: S=100 см²
Квадратическую погрешность необходимо вычислить по формуле: Таким образом, средняя квадратическая погрешность составляет - 0.10 Относительной погрешностью называется отношение абсолютной погрешности к значению самой измеренной величины. Относительная погрешность - 0.104 % Задача 1.2 Найдите среднюю квадратическую погрешность одного измерения угла и оценить точность его определения Дано: 64º34’20”
Средняя квадратическая погрешность измерения горизонтального угла определяется по результатам многократных измерений угла между двумя визирными целями. 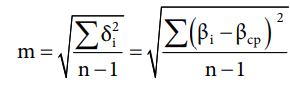 где δi – отклонения результатов отдельных измерений угла от их среднего арифметического значения; n – количество приемов измерений; βi – значение угла в i-м приеме; βср – среднее значение угла из n приемов. Ответ: 0º0’22” Задача 2.1 Сколько необходимо выполнить приемов для измерения угла прибором с точностью а, чтобы получить среднюю квадратическую погрешность b?
Ответ: 5²/1²=25 Задача 2.2 По результатам многократного измерения линии, вычислить среднее значение длины линии, среднюю квадратическую погрешность одного измерения, погрешность среднего арифметического, относительную погрешность одного измерения и относительную погрешность среднего арифметического.
l0 = 200,82 59 -1 259 249 Вероятнейшее значение длины линии L = 200,82 ±0,02 Задача 3.1 Линия d измерена 20-метровой лентой. Определить среднюю квадратическую погрешность измерения линии, если средняя квадратическая погрешность одного отложения ленты mi
Кол-во измерений: 720/20=36 0,01*36=0,36 см Средняя квадратическая погрешность измерения = 0,36 см Задача 3.2 Углы треугольника α и β измерены со средними квадратическими погрешностями соответственно mα и mβ. Найдите среднюю квадратическую погрешность третьего угла, вычисленного по двум измеренным.
Обозначим измеренные углы α и β, а искомый – γ. Запишем функцию γ = 180 – α – β, для которой найдем mγ² = mα ² + mβ ² = 36 + 9 = 45. Откуда mγ = 6,7″ Ответ: mγ = 6,7″ Задача 4.1 Даны результаты четырех измерений угла, при этом каждый результат получен, как среднее из нескольких приемов. Требуется определить наиболее надежное значение угла и среднюю квадратическую погрешность окончательного результата.
βср=(49*1,3+56*0,6+40*2,6+55*3,3)/1,3+0,6+2,6+3,3=(63,7+33,6+104+181,5)/7,8= 382,8/7,8=49,07 Ответ: Средняя квадратическая погрешность окончательного результата 56º34’49” Задача 4.2 От четырех реперов с точным значением высот путем проложения нивелирных ходов различной длины передана высота на узловую точку. Определить наиболее надежное значение высоты узловой точки и средние квадратические погрешности единицы веса и окончательного значения высоты узловой точки. 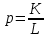 1) p=91,51 2) p=35,9 3) p=64,9 4) p=26,8 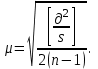 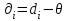 , , 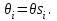 Таким образом, средние квадратические погрешности единицы веса – 54,7 Окончательное значение высоты узловой точки – 291,110 |

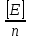 = 200,82+59/6 = 147,15
= 200,82+59/6 = 147,15