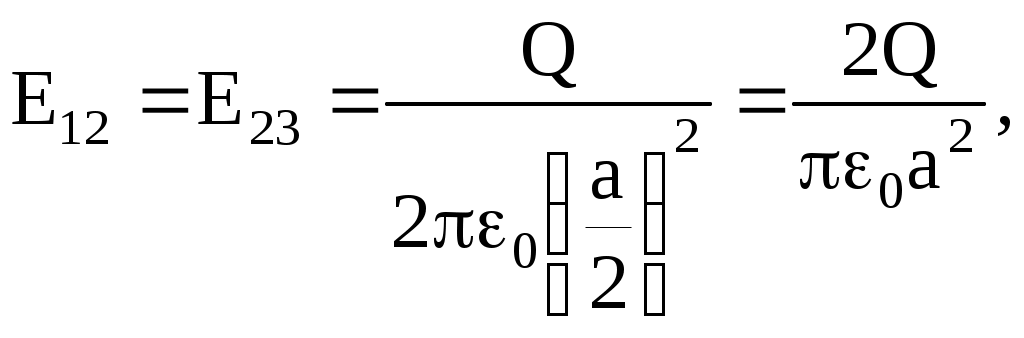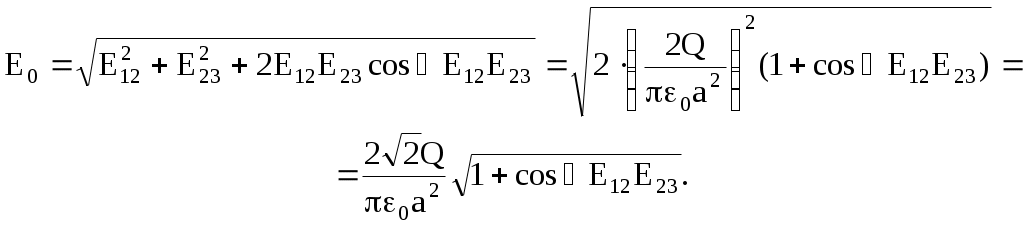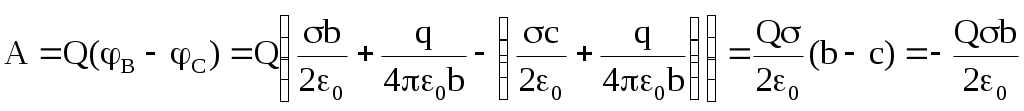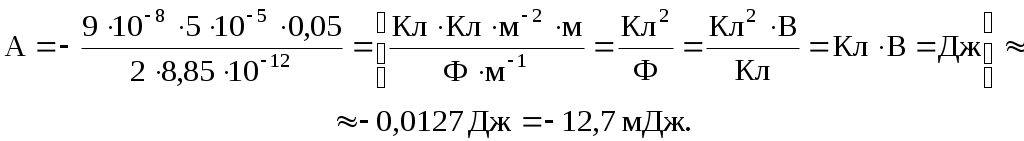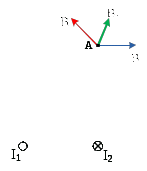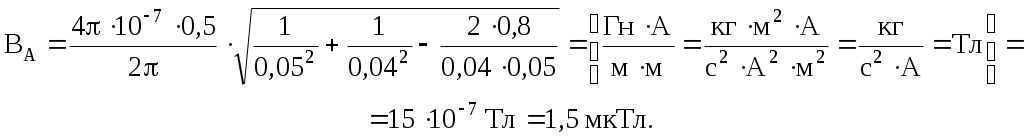Содержание
Задача №1. Напряженность электростатического поля точечных зарядов 3
Задача №2. Взаимодействие зарядов и заряженных тел 6
Задача №3. Определение индукции магнитного поля токов 8
Список литературы 10
Задача №1.
Напряженность электростатического поля точечных зарядов
В вершинах ромба со стороной а и углами = 60º и 2 = 120º соответственно (рис. 1) расположены заряды q1, q2, q3, q4. На сторонах ромба расположены равные по величине заряды Q12 и Q23. Напряженность поля в центре ромба равна Е0. Определить величину зарядов Q12 и Q23.
Дано:
q1 = q3 = –10-8 Кл
q2 = q4 = 10-8 Кл
а = 4∙10-2 м
Е0 = 3,89∙105 В/м
Найти: Q12 = Q23 = ?
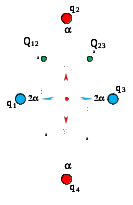
Рисунок 1
Решение:
Электростатические поля отдельных зарядов подчиняются принципу суперпозиции, согласно которому результирующий вектор напряженности поля, созданного несколькими зарядами в определенной точке, равен векторной сумме напряженностей отдельных зарядов в данной точке (см. рис. 1):
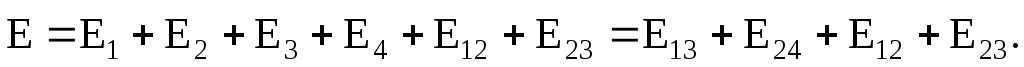
Результирующие векторы  и  , в силу того, что заряды, образующие данные поля, равны попарно и имеют одинаковый знак заряда, а векторы напряженности полей этих зарядов направлены под углом 180º друг относительно друга, равны 0; следовательно, напряженность поля в центре ромба зависит от зарядов Q12 и Q23, находящихся на сторонах ромба:
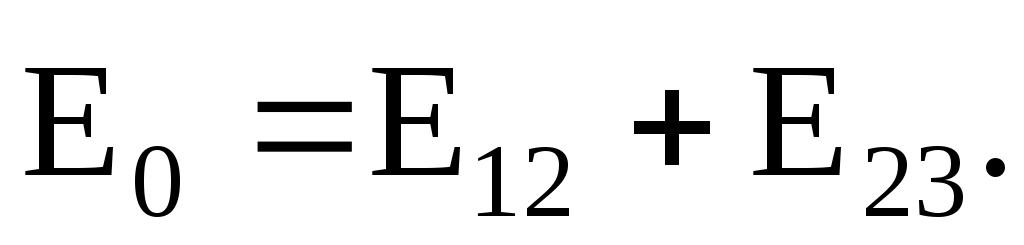
Поскольку знак данных зарядов нам заранее неизвестна, то рассмотрим два возможные случая:
1) Q12 > 0, Q23 > 0: рис. 2, а);
2) Q12 < 0, Q23 < 0: рис. 2, б).
 
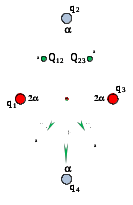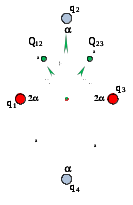
а) б)
Рисунок 2
Из геометрического построения нетрудно видеть, что в 1-м и 2-м случаях напряженность электрического поля будет одинакова по величине.
Напряженности электростатических полей, создаваемых каждым из зарядов Q12 и Q23, независимо от знака заряда, по отдельности в центре ромба, определяются по формуле
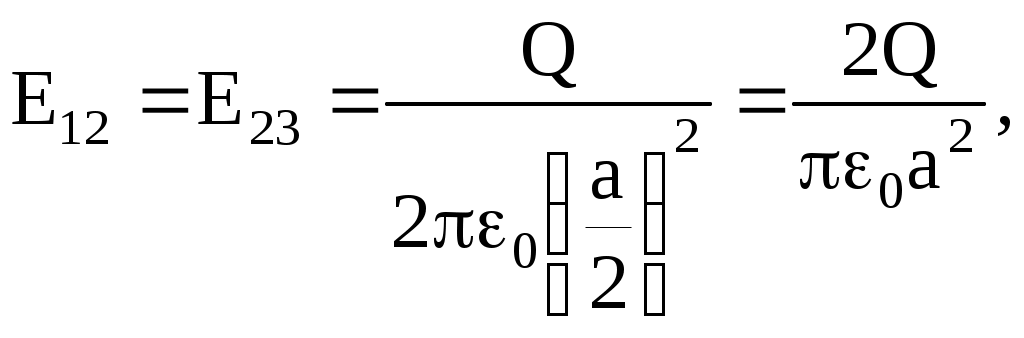
где Q = Q12 = Q23, ε0 = 8,85·10-12 Ф/м – электрическая постоянная.
Модуль суммарного вектора напряженности Е0 определится в таком случае по правилу сложения двух взаимно перпендикулярных векторов
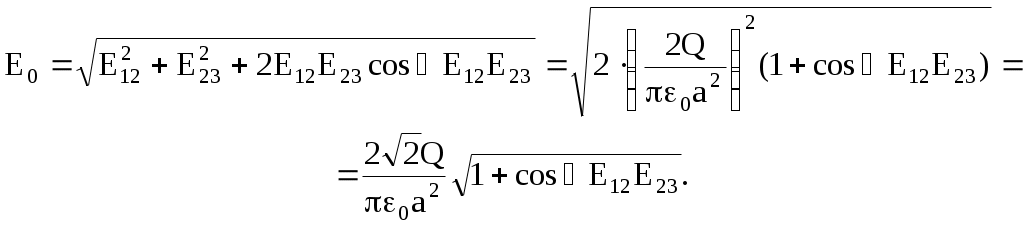
Отсюда искомая величина зарядов определяется как
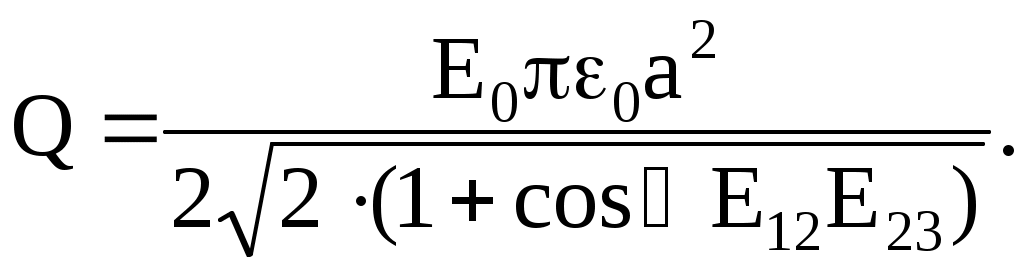
И в 1-м, и во 2-м случае угол между векторами напряженностей и равен α, следовательно, подставляя численные данные и проверяя размерность, получаем ответ:
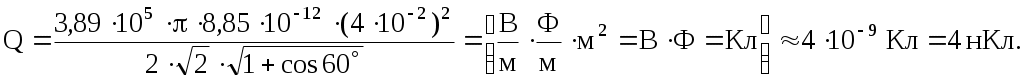
Ответ: 4 нКл.
Задача №2. Взаимодействие зарядов и заряженных тел
Заряд Q находится в точке В на расстоянии b от заряженной плоскости (поверхностная плотность заряда σ), которая, в свою очередь, располагается на расстоянии c = 2b от заряженного шара с зарядом q. При перемещении заряда Q из точки B в точку С совершается работа, так как разность потенциалов этих точек отлична от нуля. Точки В и С лежат в одной плоскости с центрами заряженных шаров (рис. 3).
Найти работу перемещения заряда Q между точками В и С.
Дано:
Q = 9∙10-8 Кл
q = 10-6 Кл
σ = 5∙10-5 Кл/м2
b = 0,05 м
с = 2b = 0,1 м
Найти: A = ?
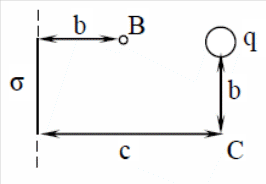
Рисунок 3
Решение:
Работу перемещения найдем из формулы
А = Q(φВ – φС).
Потенциал электростатического поля, образованного положительно заряженными плоскостью и шаром в точке В определяем как
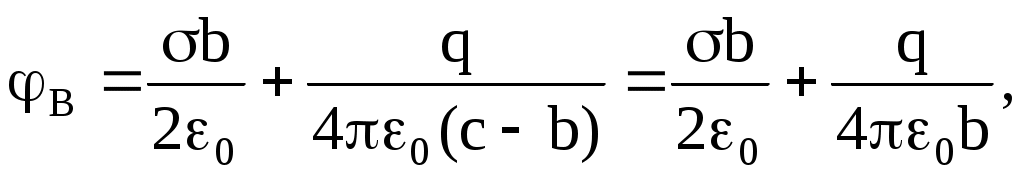
где ε0 = 8,85·10-12 Ф/м – электрическая постоянная.
Аналогично рассчитывается потенциал электростатического поля, образованного положительно заряженными плоскостью и шаром в точке С:
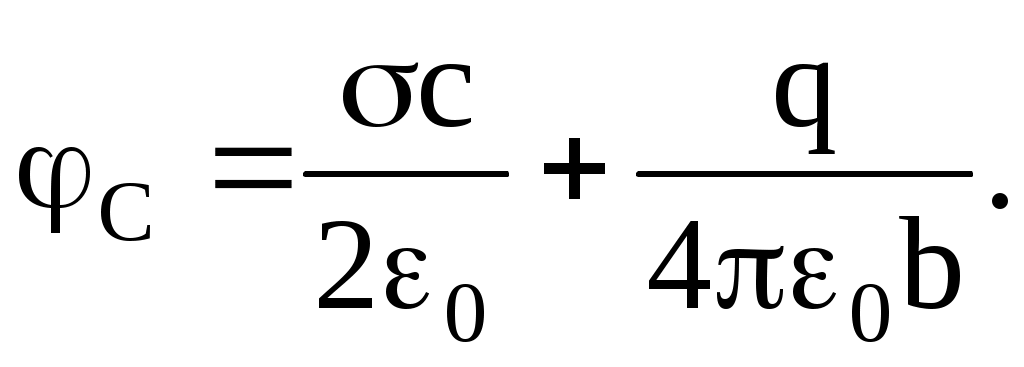
Искомая работа по перемещению заряда определится в таком случае как
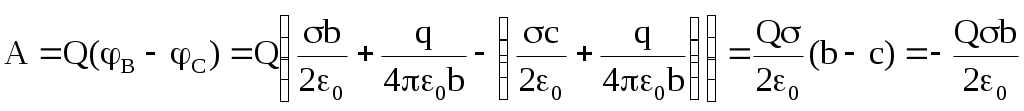
Подставляя численные данные и проверяя размерность, получаем ответ:
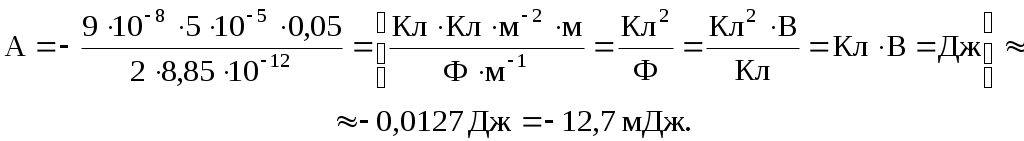
Ответ: –12,7 мДж.
Найти магнитную индукцию в точке А (рис. 4).
 
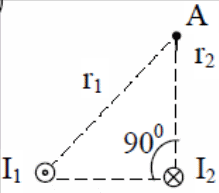
Рисунок 4
Дано:
r1 = 5 см = 0,05 м
r2 = 4 см = 0,04 м
I1 = I2 = 0,5 A
Найти: ВА = ?
Решение:
Покажем направления векторов индукции магнитных полей (рис. 5).
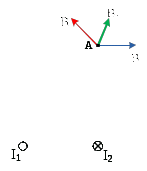
Рисунок 5
Направления векторов магнитной индукции для каждого проводника определяются по правилу буравчика (правого винта).
Магнитные поля В1 и В2 (принимая для удобства I1 = I2 = I) нетрудно найти по формуле для магнитной индукции бесконечно длинного прямолинейного проводника:
 
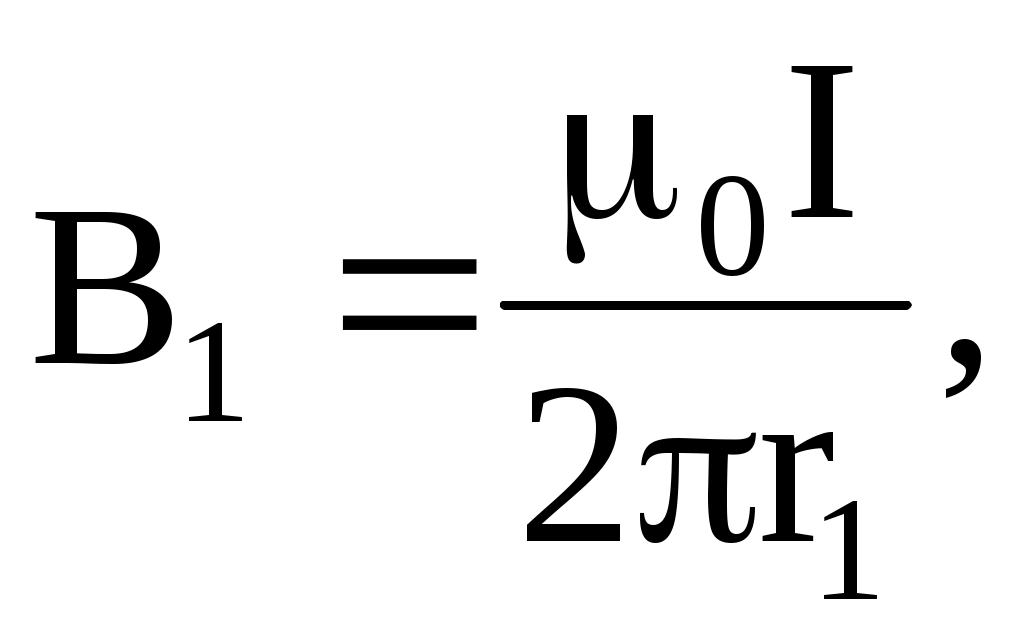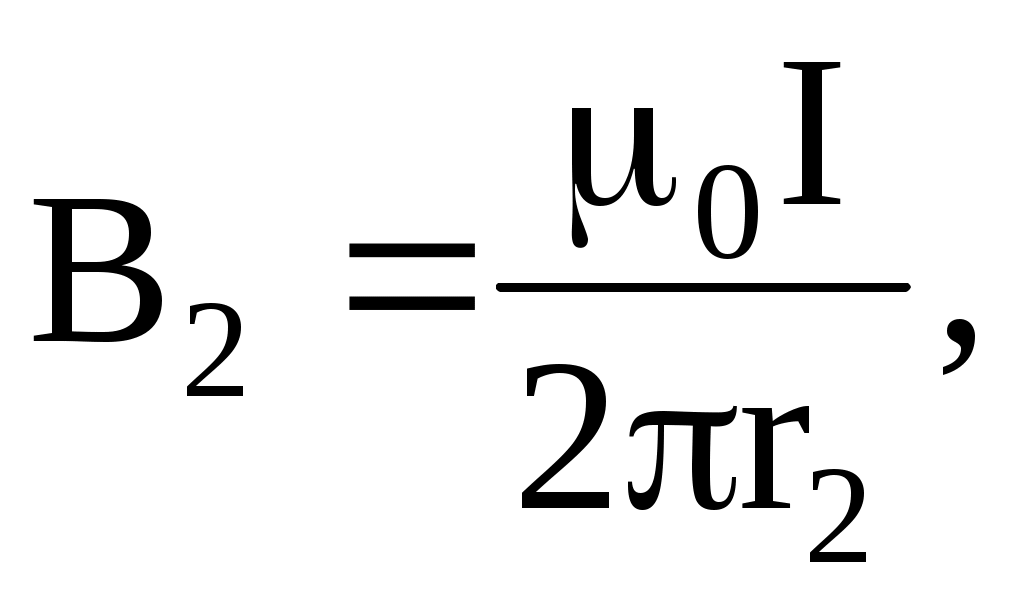
где μ0 = 4π·10-7 Гн/м – магнитная постоянная.
Магнитные поля подчиняются принципу суперпозиции. Поэтому равнодействующая полей В1 и В2
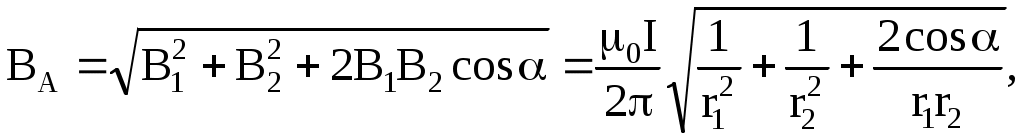
где α – угол, образуемый векторам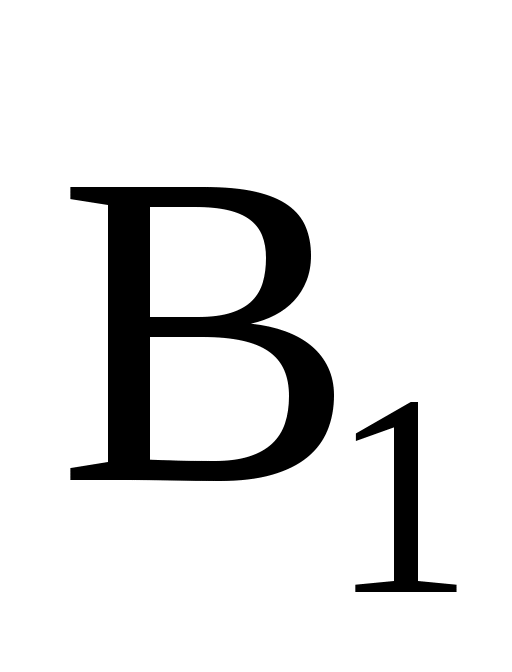и  и 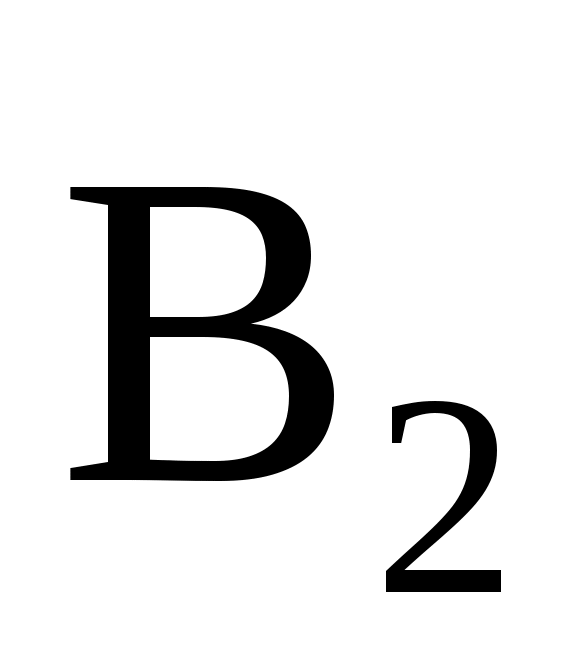 . Для вычисления данного угла определим угол прямоугольного треугольника, образуемый сторонами r1 (гипотенуза) и r2 (прилежащий углу катет), исходя из определения косинуса угла:
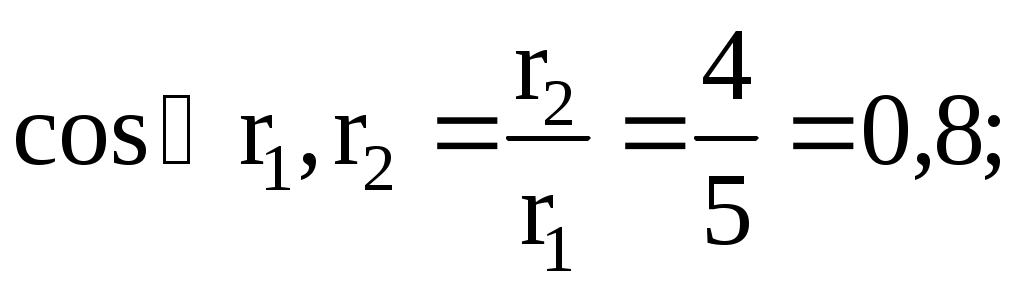
отсюда
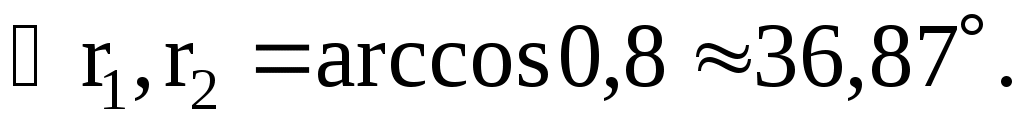
Тогда искомый угол, образуемый векторам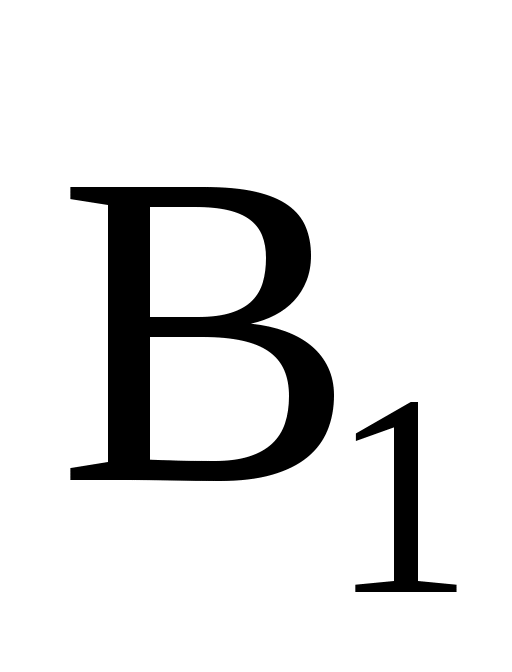и и 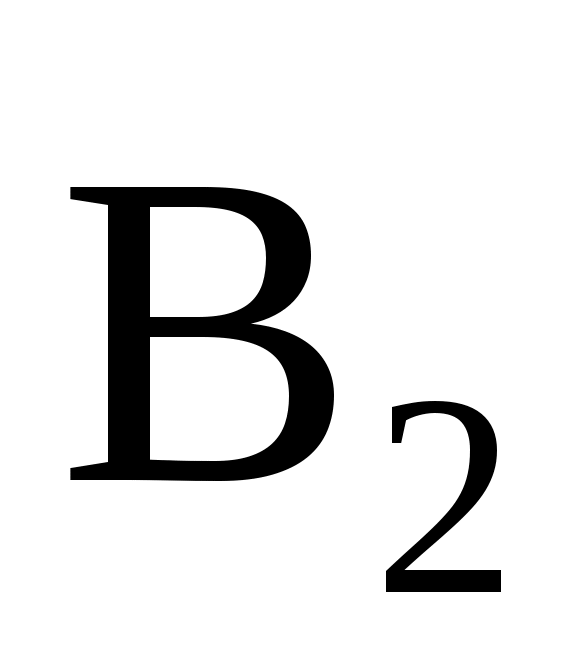, нетрудно определить как
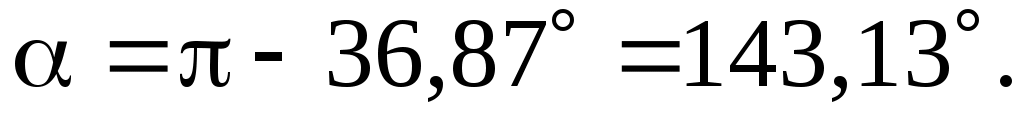
Соответственно, косинус данного угла
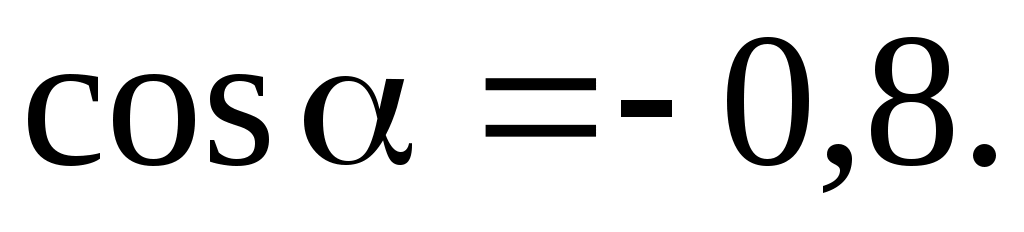
Подставляя численные данные и проверяя размерность, получаем ответ:
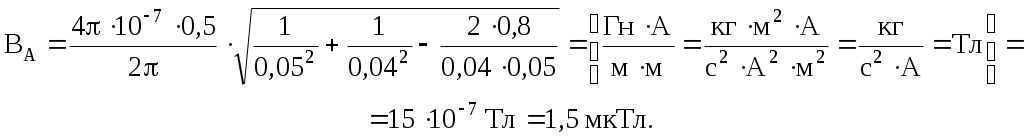
Ответ: 1,5 мкТл.
Список литературы
Чертов А.Г. Задачник по физике./ А.Г. Чертов, А.А. Воробьев. – М.: Высшая школа, 1988. – 527 с.
Волькенштейн В.С. Сборник задач по общему курсу физики./ В.С. Волькенштейн. – СПб.: Книжный мир, 2003. – 327 с.
Детлаф А.А. Курс физики: уч. пособ. для втузов./ А.А. Детлаф, Б.М. Яворский. – М.: Высшая школа, 2002. – 718 с.
Трофимова Т.И. Курс физики: уч. пособ. для вузов / Т.И. Трофимова. – М.: Высшая школа, 2000. – 542 с.
|
Скачать 475 Kb.