Задание на контрольную работу ИМ. Задача 1. Обработка результатов однократных прямых измерений Аналоговыми приборами класса точности k
 Скачать 92.85 Kb. Скачать 92.85 Kb.
|
|
Задание для выполнения контрольной работы по дисциплине «Метрология, стандартизация и сертификация» для студентов заочной формы обучения специальности ИМ Доцент кафедры «Теоретическая электротехника» Комяков Александр Анатольевич Омск 2020 г. Задача №1. Обработка результатов однократных прямых измерений Аналоговыми приборами класса точности kп с номинальным значением IN для амперметра или UN для вольтметра и шкалой, рассчитанной на 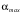 = 150 делений, измеряется ток или напряжение в цепи, содержащей сопротивление r. Сопротивление r имеет погрешность = 150 делений, измеряется ток или напряжение в цепи, содержащей сопротивление r. Сопротивление r имеет погрешность 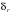 . Измерение выполняется при температуре окружающей среды Токр, оС. Отсчетное устройство показывает . Измерение выполняется при температуре окружающей среды Токр, оС. Отсчетное устройство показывает 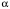 делений с округлением при отсчете до половины деления шкалы. Внутреннее сопротивление амперметра равно rA, а вольтметра – rV. Температурная погрешность не превышает значения m основной на каждые делений с округлением при отсчете до половины деления шкалы. Внутреннее сопротивление амперметра равно rA, а вольтметра – rV. Температурная погрешность не превышает значения m основной на каждые 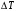 оС и рассчитывается по формуле: оС и рассчитывается по формуле: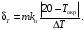 (1.1) (1.1)По данным варианта (табл. 1.1) записать результат измерения тока (рис. 1.1) или напряжения (рис. 1.2). Доверительную вероятность принять равной 0,95. 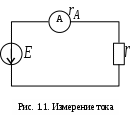 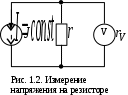 Таблица 1.1 Исходные данные для задачи №1
Задача №2. Обработка результатов многократных прямых измерений Для определения достоверного значения измеряемого напряжения с заданной доверительной вероятностью Рд выполнен в одинаковых условиях и одним и тем же прибором ряд повторных измерений напряжения в количестве n = 11. Измеренные значения напряжения (в мВ) рассчитываются по формуле: 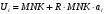 , (2.1) , (2.1)где 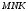 – последние три цифры номера шифра студента; – последние три цифры номера шифра студента;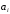 – случайные числа в интервале от 0 до 1, определяемые по табл. 2.1; – случайные числа в интервале от 0 до 1, определяемые по табл. 2.1;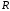 – безразмерный коэффициент, определяемый по табл. 2.1. – безразмерный коэффициент, определяемый по табл. 2.1.Например, последние цифры шифра студента 403, тогда измеренные значения напряжения будут равны 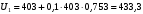 мВ, мВ, 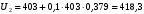 мВ и т.д. мВ и т.д. По данным табл. 2.1, считая, что погрешности распределены по закону Стьюдента, определить: а) среднее значение измеряемого напряжения; б) абсолютные погрешности и среднее квадратическое отклонение погрешности заданного ряда измерений; в) среднее квадратическое отклонение среднего арифметического; г) результат измерения и доверительный интервал для заданной доверительной вероятности. При расчете принять, что систематические погрешности в результате измерения отсутствуют. Таблица 2.1 Исходные данные для решения задачи №2
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 %
% %
%
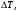 оС
оС