Тех мех натт. Задача 1 Определить реакции двухопорной балки, если F20H, M20Hm, g4Hm

• Название: Задача 1 Определить реакции двухопорной балки, если F20H, M20Hm, g4Hm
• Анкор: Тех мех натт
• Дата: 13.11.2022
• Размер: 495.93 Kb.
• Имя файла: TM0.docx
• Тип: Задача; #785336

Задача 1

Определить реакции двухопорной балки, если F=20H, M=20Hm, g=4H/m



Q=6g=24H

Fx=Fcos30=20x0,866=17,32H

Fy=Fcos60=20x0,5=10H

∑Fx=0; ∑Fx=-Xa+Fx=0

Xa=Fx=17,32H

∑Ma(F)=0; ∑Ma(F)=Fy+M+7Q-10Yb

Yb=(Fy+M+7Q)/10=(10+20+7x24)/10=19,8H

∑Mb(F)=0; ∑Mb(F)=3Q-M+9Fy+10Ya

Ya=(3Q-M+9Fy)/10=(3x24-20+9x10)/10=14,2H

∑Fy=0; ∑Fy=Ya-Fy-Q+Yb=14,2-10-24+19,8=0

Задача 2

В  привод  транспортёра  входит  ременная  передача,  ведомый шкив  которой вращается с частотой n₂=160 об/мин через 4 секунды равнопеременного вращения из состояния покоя. Определить скорость перемещения ленты транспортёра V через 5 секунд от начала разгона. Определить также расстояние S, на которое переместится груз, находящийся на ленте за это же время, если известно: d₂=200 мм, d₃=300 мм.



Решение:

Угловая скорость ведомого вала через 4 секунды равнопеременного вращения из состояния покоя



Уравнение равноускоренного вращения



Угловое ускорение



Угловая скорость барабана транспортера через 5 секунд после разгона



Линейная скорость транспортера через 5 секунд после разгона



Ускорение транспортера определим из уравнения скорости



Перемещение груза за 5 с найдем из уравнения движения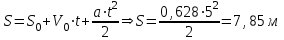



Задача 3

Ручной подъемный механизм имеет рукоятку длиной l=280 мм. Рабочий, прикладывая к ее концу силу F=180Н перпендикулярно рукоятке, вращает рукоятку с угловой скоростью ω=0,8 с-1. Определить работу, совершаемую рабочим в течение 5 мин.



Решение:

Основная формула работы:



где N - мощность, t - затраченное время.

Мощность выразим через момент силы - М и угловую скорость -  ω:



Момент сил можно выразить через приложенную силу и плечо:


t = 5 мин = 5 · 60 = 300 c.

Тогда: 





Ответ: затраченная работа 12096 Дж.

Задача 5

На стальном валу постоянного поперечного сечения жестко закреплены четыре шкива. Ведущий шкив сообщает валу вращающий момент М₂=2700 Нм. Моменты, снимаемые с вала остальными шкивами : М₁=500 Нм, М₃=1300 Нм, М₄=900 Нм. Построить эпюру крутящих моментов и определить требуемый диаметр вала, если [τ]=40 МПа. Как надо расположить шкивы, чтобы при этих же данных получить наименьший диаметр вала?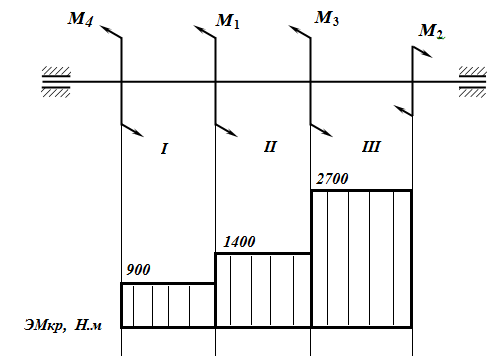



Решение:

1. 
   Разбиваем вал на участки и определяем крутящие моменты
   

Вал имеет три участка, границами которых являются сечения, в которых приложены внешние моменты. В пределах каждого участка значение крутящего момента постоянно.







2. Определяем диаметр вала из условия прочности



W_x момент сопротивления при кручении



3. Наименьший диаметр вала получится, если расположить шкивы так, чтобы максимальный крутящий момент был минимальным.

Наиболее целесообразно такое размещение колес, при котором наибольшие положительные и отрицательные значения крутящих моментов на участках будут по возможности одинаковыми. Из этих соображений ведущий шкив, передающий момент 2700Н·м, помещаем ближе к центру вала, ведомые шкивы 3 и 4 размещаем слева и справа от ведущего.






Задача 6

Для заданной стальной двухопорной балки определить реакции опор, построить эпюры поперечных сил, изгибающих моментов и определить из условия прочности необходимые размеры поперечногосечения балки в форме прямоугольника. Для прямоугольного сечения бруса принять h= 3b. [σ] = 180 Н/мм².

Дано: F₁=5 кН, F₂=8кН, М=6 кН·м



Решение

1. 
   Составляем уравнение равновесия параллельной системы сил, из которых определяем опорные реакции балки:
   

F₁·0,8 + M - F₂· 2,4 + R_C·1,5=0 (1)

F₁·2,3 + M –R_B · 1,5 - F₂·0,9 =0 (2)

Решаем систему уравнений.

Из уравнения (1) находим R_C:



Из уравнения (2) находим R_B:



Для проверки правильности решения составим сумму протекций всех сил на ось Y

2. 
   Определяем значения поперечной силы Q в характерных сечениях балки, которые обозначим буквами А, В, С, D.
   

Q_A= -F₁= - 5 кН,

Q_B^слева = -F₁=- 5 кН,

Q_B^справа =-F₁ +R_B= - 5+6,87=1,87 кН,

Q_C^слева =-F₁ +R_B= - 5+6,87=1,87 кН,

Q_C^справа =-F₁ +R_B+R_C= - 5+6,87+6,13=8 кН

Q_D = F₂= 8 кН

3. 
   Вычисляем изгибающие моменты в тех же характерных точках А, В, С, D и строим их эпюру:
   

М_A =0,

М_B^слева= - F₁ ·0,8 =- 5·0,8 = -4 кН·м,

М_B^справа = - F₁ ·0,8 =- 5·0,8 = -4 кН·м,

М_C^слева = - F₁ ·2,3 +R_B·1,5= - 5·2,3+6,87·1,5 = -1,2 кН·м,

М_C^справа = - F₁ ·2,3 +R_B·1,5= - 5·2,3+6,87·1,5 = -1,2 кН·м,

М_D= - F₁ ·3,2 +R_B·2,4+R_С·0,9= - 5·3,2+6,87·2,4+6,13·0,9 =6 кН·м,

Определяем размеры поперечного сечения балки, для чего используем условие прочности при изгибе

σ = М_И /W_х = [σ],

где W_х - осевой момент сопротивления является геометрической характеристикой прочности поперечного сечения,

М_И - взятый по абсолютному значению максимальный изгибающий момент.

М_max = 6 кН∙м = 6∙10³ Н∙ м;

6· 10³/ W_х ≤ 180

отсюда требуемый момент сопротивления W_х = 33,3 мм³.

Сечение – прямоугольник, h=3b