эконометрика. Вариант1. Задача 1 По 20 предприятиям региона изучается зависимость выработки продукции на
 Скачать 0.71 Mb. Скачать 0.71 Mb.
|
1 2 Ситуационная (практическая) задача № 1 По 20 предприятиям региона изучается зависимость выработки продукции на одного работника y (тыс. руб.) от удельного веса рабочих высокой квалификации в общей численности рабочих x1 (% от стоимости фондов на конец года) и от ввода в действие новых основных фондов x2 (%). 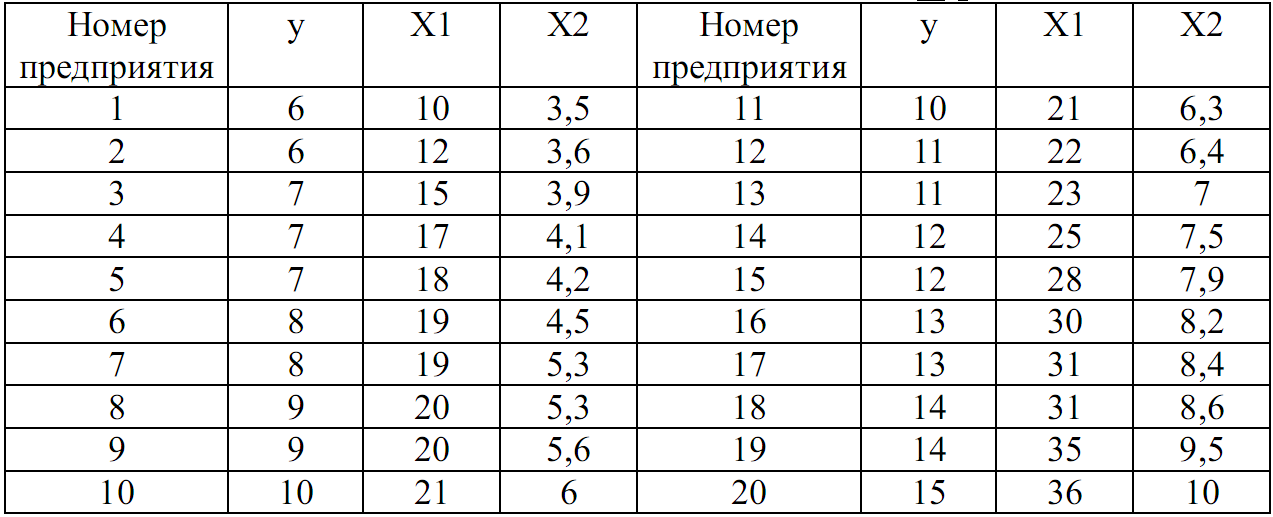 Требуется: Требуется: 1. Построить корреляционное поле между выработкой продукции на одного работника и удельным весом рабочих высокой квалификации. Выдвинуть гипотезу о тесноте и виде зависимости между показателями X1 и Y. 2. Оценить тесноту линейной связи между выработкой продукции на одного работника и удельным весом рабочих высокой квалификации с надежностью 0,9. 3. Рассчитать коэффициенты линейного уравнения регрессии для зависимости выработки продукции на одного работника от удельного веса рабочих высокой квалификации. 4. Проверить статистическую значимость параметров уравнения регрессии с надежностью 0,9 и построить для них доверительные интервалы. 5. Рассчитать коэффициент детерминации. С помощью F -критерия Фишера оценить статистическую значимость уравнения регрессии с надежностью 0,9. 6. Дать точечный и интервальный прогноз с надежностью 0,9 выработки продукции на одного работника для предприятия, на котором высокую квалификацию имеют 24% рабочих. 7. Рассчитать коэффициенты линейного уравнения множественной регрессии и пояснить экономический смысл его параметров. 8. Проанализировать статистическую значимость коэффициентов множественного уравнения с надежностью 0,9 и построить для них доверительные интервалы. 9. Найти коэффициенты парной и частной корреляции. Проанализировать их. 10. Найти скорректированный коэффициент множественной детерминации. Сравнить его с нескорректированным (общим) коэффициентом детерминации. 11. С помощью F -критерия Фишера оценить адекватность уравнения регрессии с надежностью 0,9. 12. Дать точечный и интервальный прогноз с надежностью 0,9 выработки продукции на одного работника для предприятия, на котором высокую квалификацию имеют 24% рабочих, а ввод в действие новых основных фондов составляет 5%. 13. Проверить построенное уравнение на наличие мультиколлинеарности по: критерию Стьюдента; критерию χ2. Сравнить полученные результаты. Решение 1. Построить корреляционное поле между выработкой продукции на одного работника и удельным весом рабочих высокой квалификации. Выдвинуть гипотезу о тесноте и виде зависимости между показателями X1 и Y. Построим поле рассеяния: 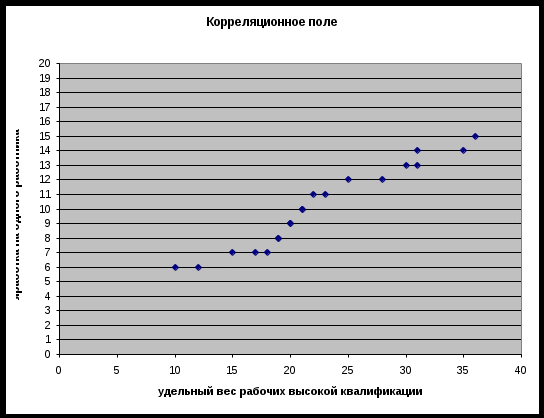 Рис. 1. Корреляционное поле между валовым доходом и стоимостью основных фондов На основе визуального анализа построенных полей рассеяния можно выдвинуть гипотезу о линейной зависимости валового дохода от стоимости основных фондов. Математически данная зависимость запишутся в виде: 2. Оценить тесноту линейной связи между выработкой продукции на одного работника и удельным весом рабочих высокой квалификации с надежностью 0,9 Составим расчетную таблицу: Табл.1
Найдем коэффициент парной корреляции для проверим, существенно ли отличается найденный коэффициент корреляции от нуля. Найдем: 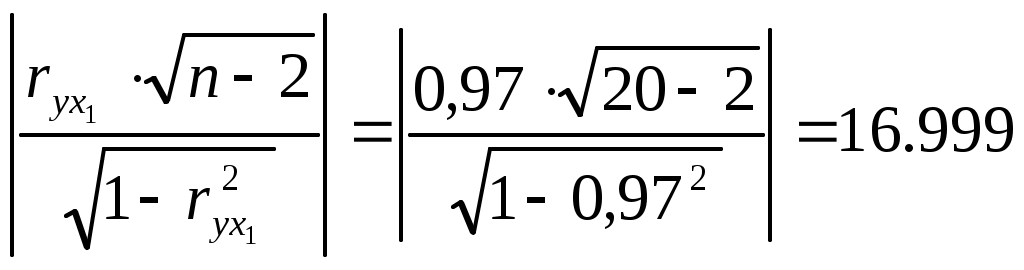 Сравним с квантилем распределения Стьюдента Т.к. 16,999>1,7341, то коэффициент корреляции 3. Рассчитать коэффициенты линейного уравнения регрессии для зависимости выработки продукции на одного работника от удельного веса рабочих высокой квалификации. Методом наименьших квадратов найти оценки линейных уравнений регрессии: 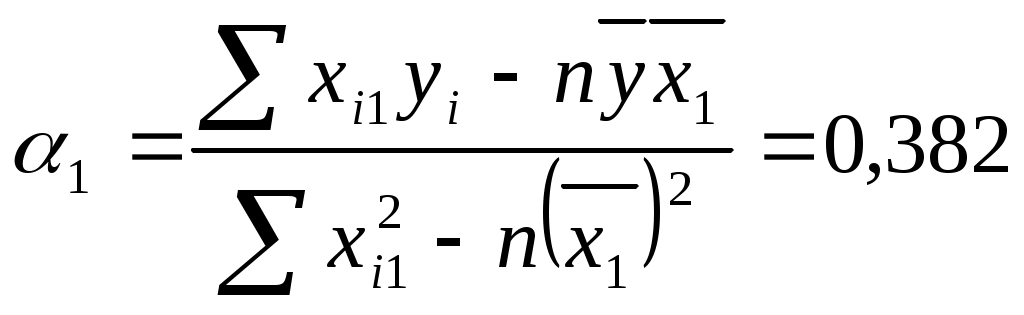 таким образом, получаем уравнение регрессии: 4. Проверить статистическую значимость параметров уравнения регрессии с надежностью 0,9 и построить для них доверительные интервалы. Коэффициент детерминации: Фактическое значение F-статистики Фишера Для оценки статистической значимости коэффициентов регрессии найдем Найдем доверительную полосу для уравнения регрессии Табл.2
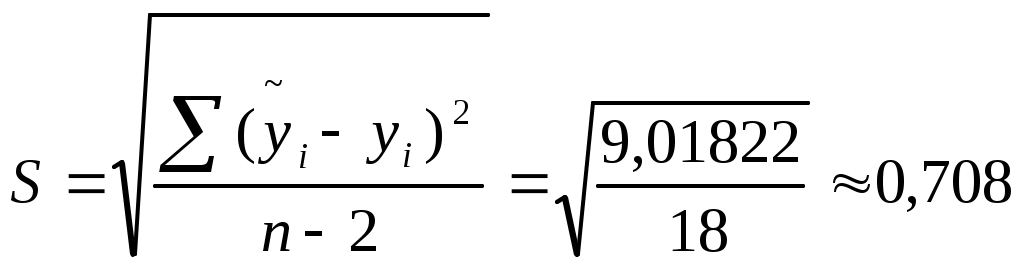 , для каждого xi1 рассчитаем , для каждого xi1 рассчитаем 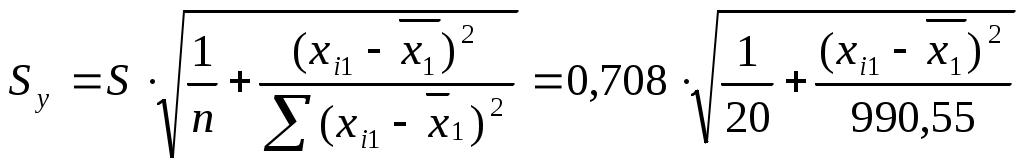 , , Значения 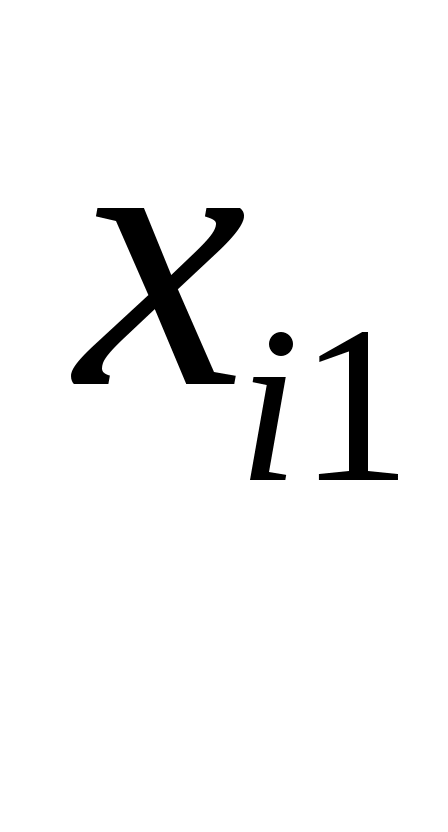 . Линию регрессии и доверительную полосу изобразим на рисунке 2 . Линию регрессии и доверительную полосу изобразим на рисунке 2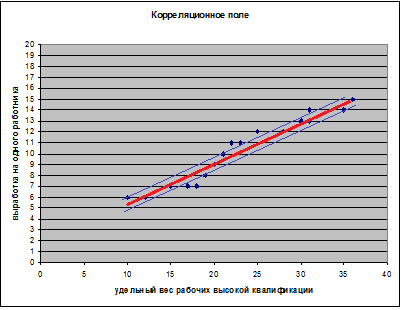 Рис. 2. Линия регрессии и доверительная полоса 5.Рассчитать коэффициент детерминации. С помощью F -критерия Фишера оценить статистическую значимость уравнения регрессии с надежностью 0,9. Коэффициент детерминации и фактическое значение F -критерия рассчитаны в п.4 При уровне значимости 0,1 табличное значение Т.к. 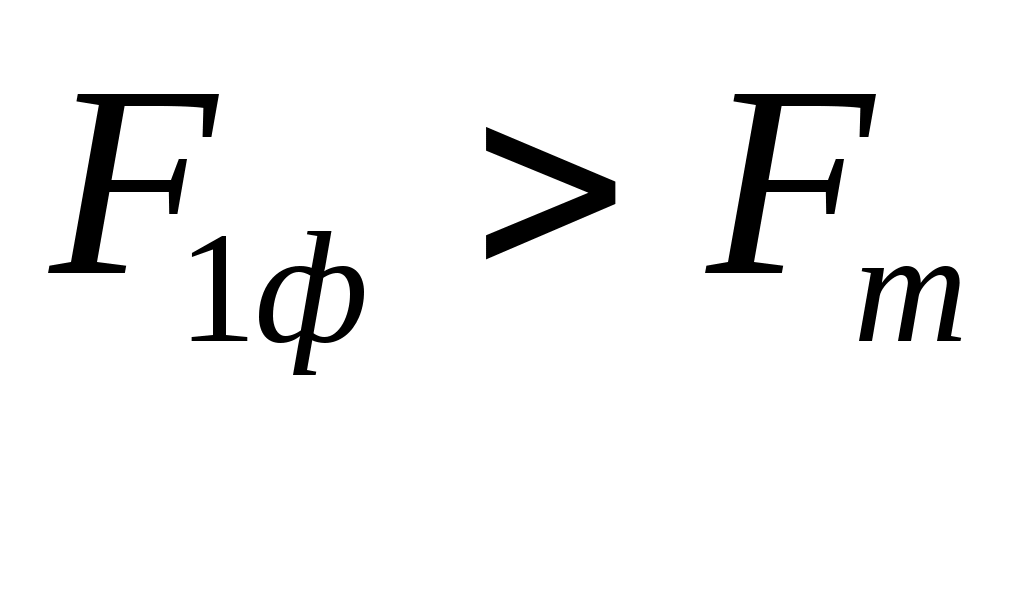 , то признается статистическая значимость уравнения регрессии. , то признается статистическая значимость уравнения регрессии.6. Дать точечный и интервальный прогноз с надежностью 0,9 выработки продукции на одного работника для предприятия, на котором высокую квалификацию имеют 24% рабочих. Точечный прогноз: Интервальный: 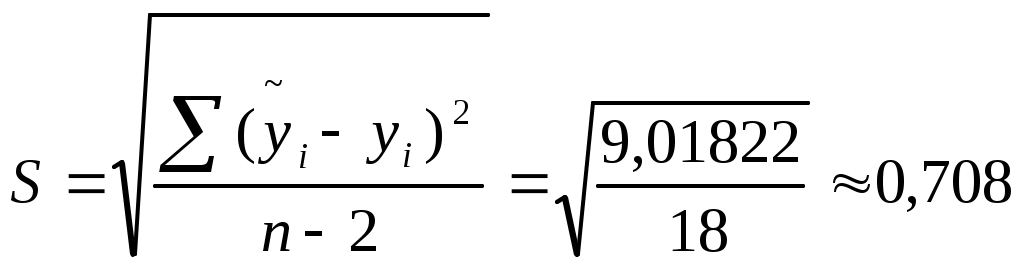 , для каждого xi1 рассчитаем , для каждого xi1 рассчитаем 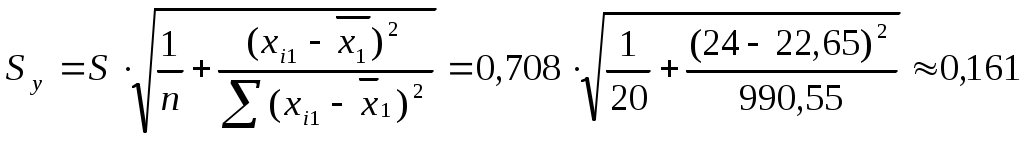 7. Рассчитать коэффициенты линейного уравнения множественной регрессии и пояснить экономический смысл его параметров. По методу наименьших квадратов найдем оценки коэффициентов множественной линейной регрессионной модели Составим матрицы 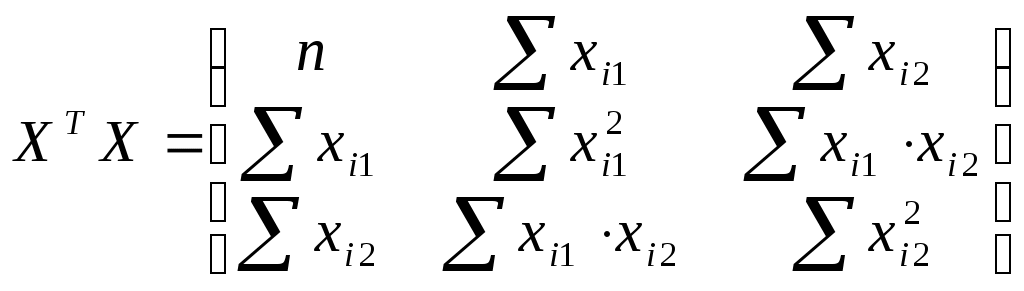 и и 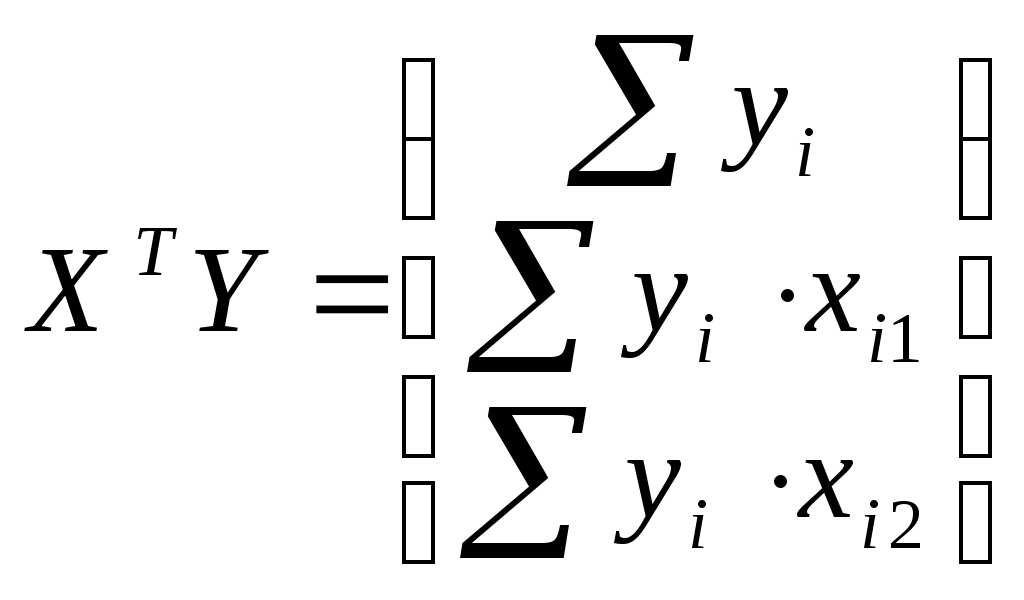 Для этого составим вспомогательную таблицу: (таблица 3)
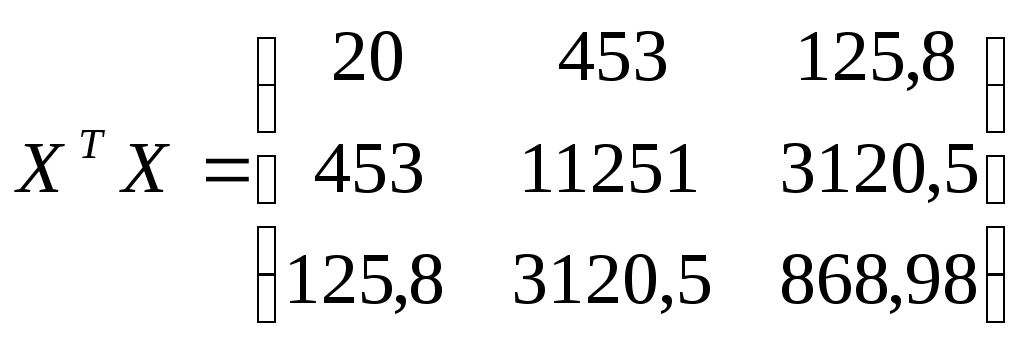 ; ; 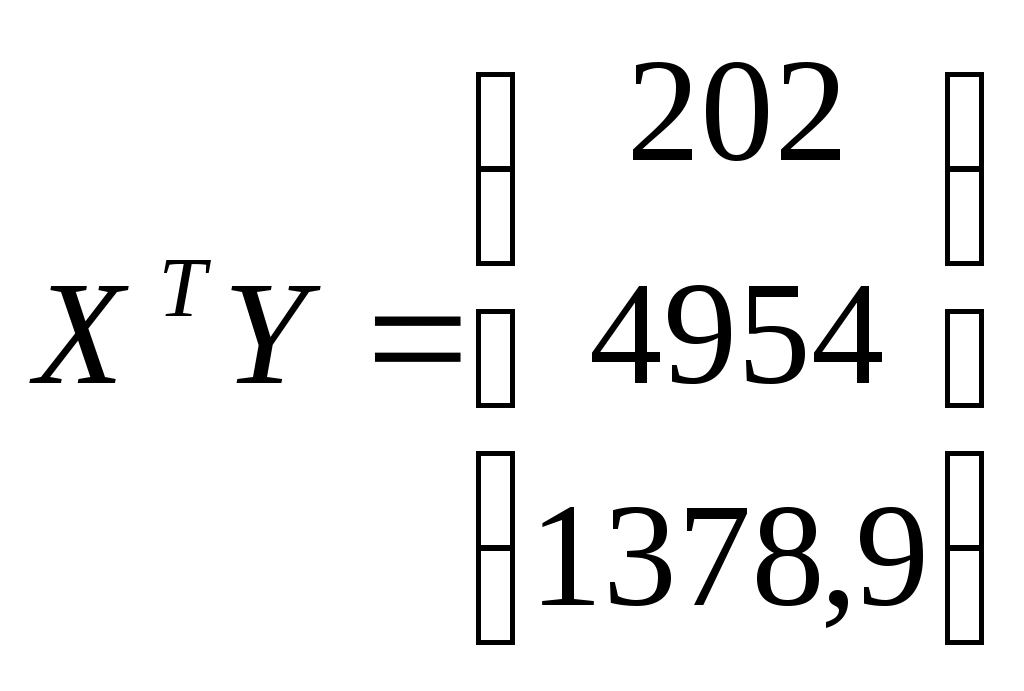 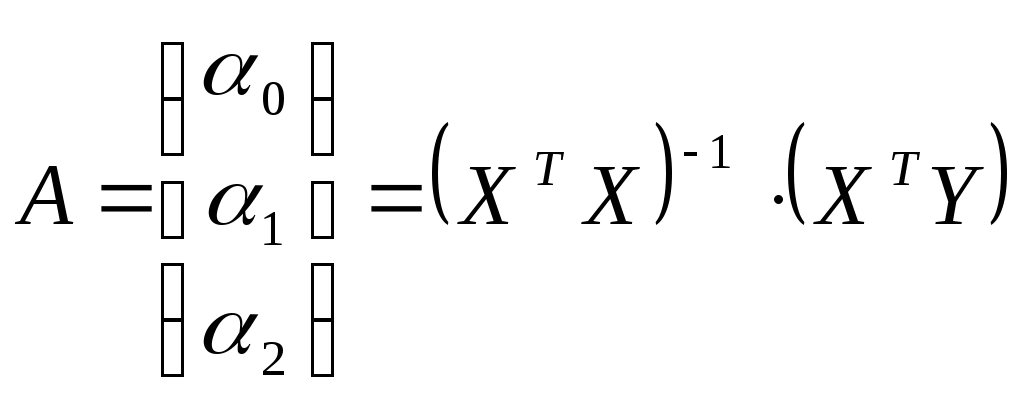 Обратная матрица  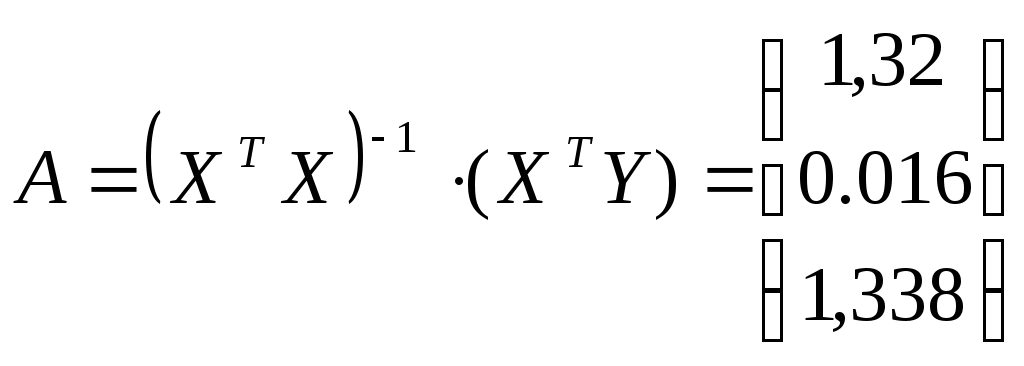 таким образом, получаем уравнение регрессии: таким образом, получаем уравнение регрессии:Коэффициент Коэффициент 8. Проанализировать статистическую значимость коэффициентов множественного уравнения с надежностью 0,9 и построить для них доверительные интервалы. Для вычисления коэффициента детерминации составим таблицу: (таблица 4) 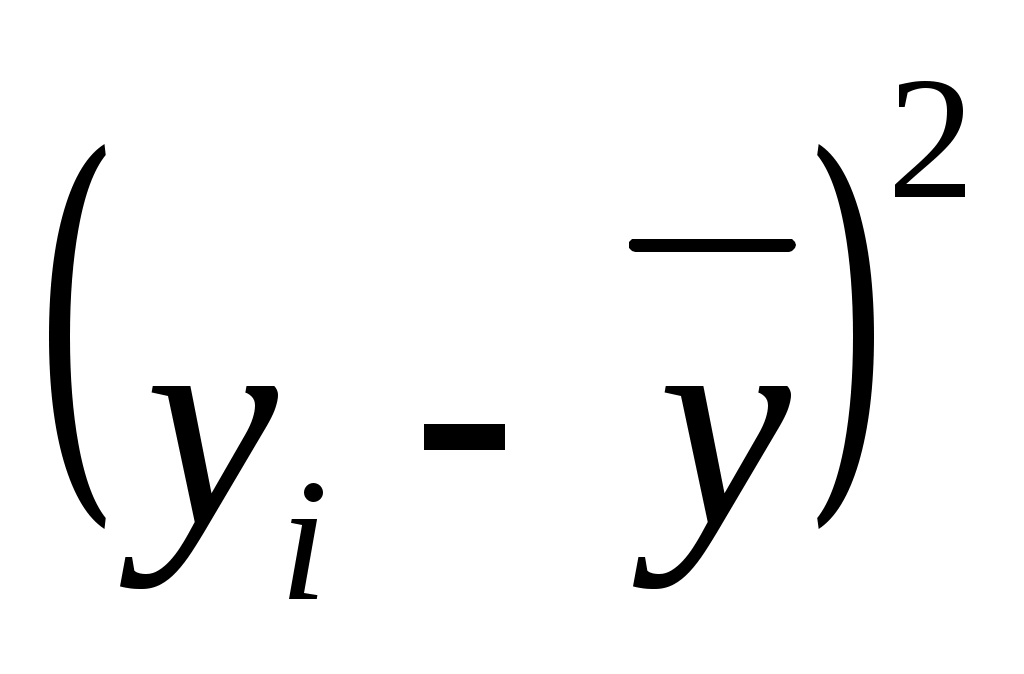
Значимость параметров уравнения регрессии оценивается с помощью t-критерия Стьюдента. Для расчета t-статистик коэффициентов необходимо рассчитать их стандартные ошибки: где Получаем: Тогда t-статистики коэффициентов равны: При уровне значимости Т.к. Интервальная оценка для коэффициента 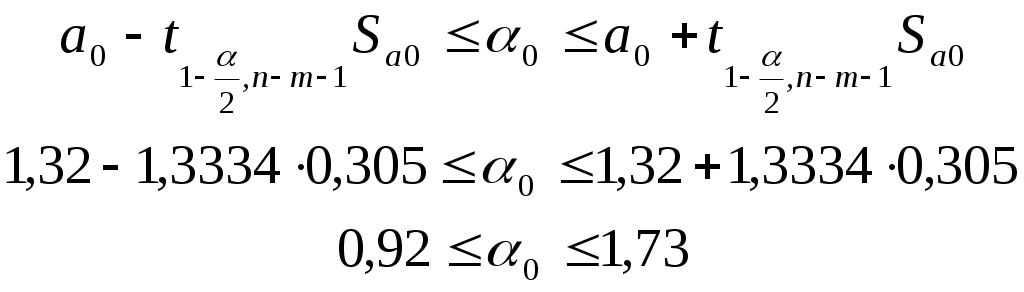 Таким образом, истинное значение Интервальная оценка для коэффициента 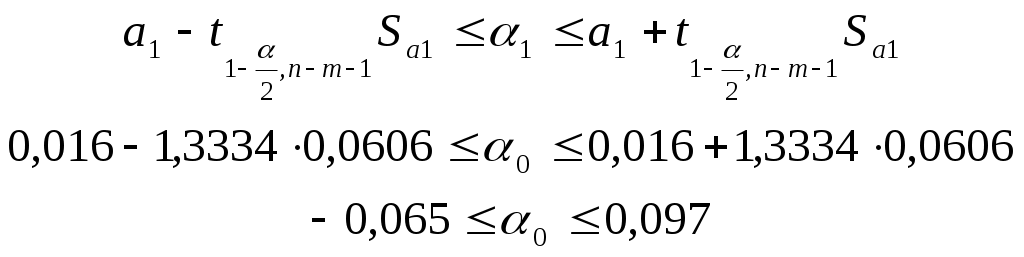 Таким образом, истинное значение Интервальная оценка для коэффициента 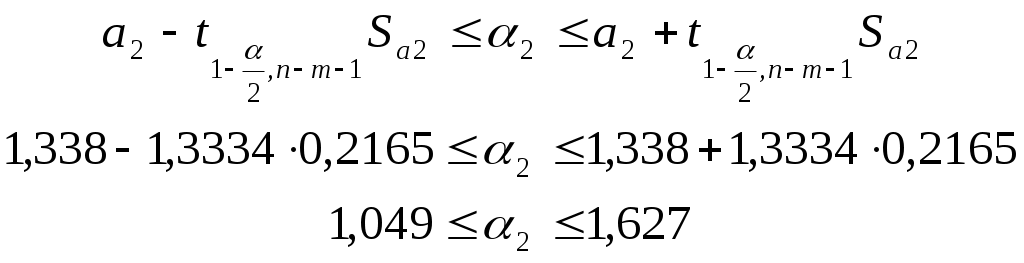 Таким образом, истинное значение 9. Найти коэффициенты парной и частной корреляции. Проанализировать их. Парные коэффициенты корреляции применяются для измерения тесноты связи между двумя из рассматриваемых переменных (без учета их взаимодействия с другими переменными) – результаты промежуточных вычислений – см. табл. 3. 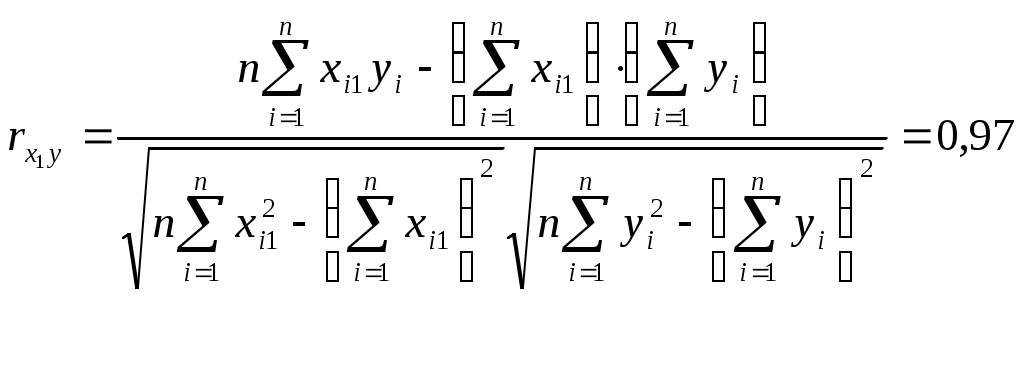 Промежуточные вычисления приведены в таблице 4. В данном случае 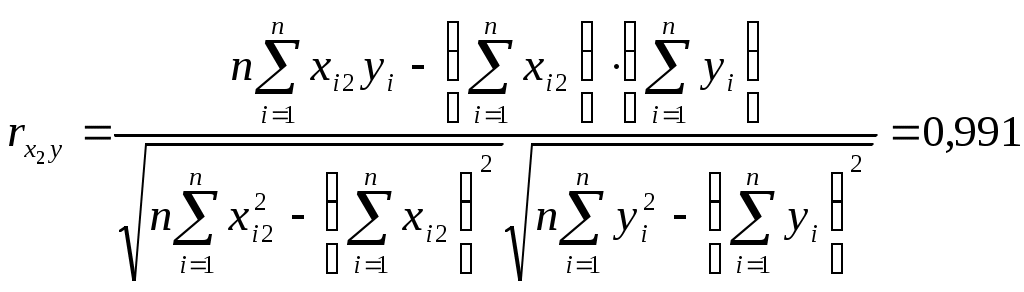 В данном случае 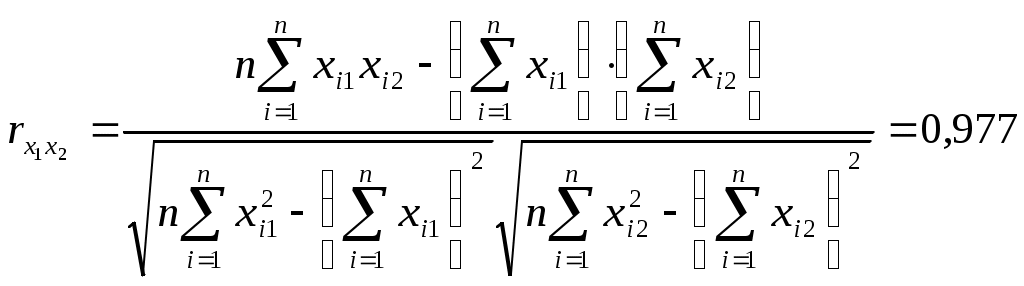 В данном случае Коэффициент частной корреляции измеряет тесноту линейной связи между отдельным фактором и результатом при устранении воздействия прочих факторов модели: 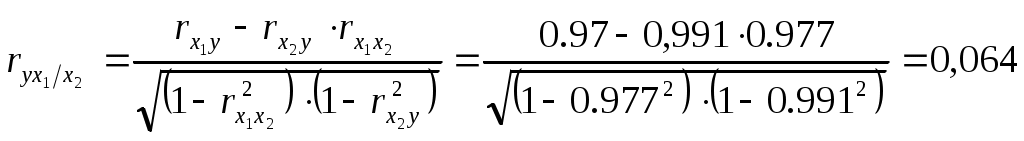 Полученное значение говорит о том, что между выработкой продукции и удельным весом рабочих высокой квалификации при фиксированном значении ввода в действие основных фондов существует слабая прямая зависимость. 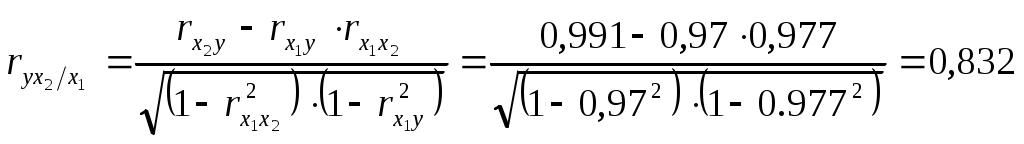 Полученное значение говорит о том, что между выработкой и вводом в действие основных средств при фиксированном значении удельного веса квалифицированных рабочих существует тесная прямая зависимость. 10. Найти скорректированный коэффициент множественной детерминации. Сравнить его с нескорректированным (общим) коэффициентом детерминации. Коэффициент множественной детерминации равен: 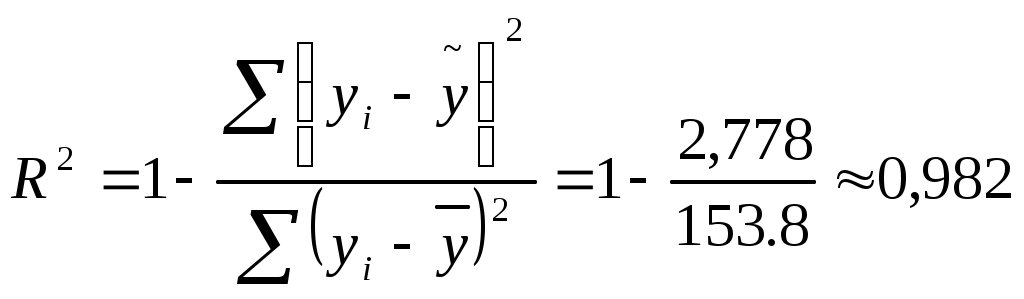 Следовательно, регрессия y на x1 и x 2 объясняет 98,2% колебаний значений у. Это свидетельствует о значительном суммарном влиянии независимых переменных x1 и x 2 на зависимую переменную у. Для того чтобы была возможность сравнивать модели с разным числом факторов так, чтобы число регрессоров (факторов) не влияло на статистику где n – количество наблюдений; m – количество факторных признаков. Получаем: Данный показатель всегда меньше единицы, но теоретически может быть и меньше нуля (только при очень маленьком значении обычного коэффициента детерминации и большом количестве факторов). Поэтому теряется интерпретация показателя как «доли». Тем не менее, применение показателя в сравнении вполне обоснованно. 11. С помощью F -критерия Фишера оценить адекватность уравнения регрессии с надежностью 0,9. Качество уравнения также оценивается с помощью F-теста. Расчетное значение F-критерия: В данном случае Критическое значение F-критерия при уровне значимости Т.к. 12. Дать точечный и интервальный прогноз с надежностью 0,9 выработки продукции на одного работника для предприятия, на котором высокую квалификацию имеют 24% рабочих, а ввод в действие новых основных фондов составляет 5%. При Интервальный прогноз среднего значения накоплений домохозяйств: где Тогда Пусть Таким образом, для предприятия, на котором высокую квалификацию имеют 24% рабочих, а ввод в действие новых основных фондов составляет 5% с вероятностью 90% выработка попадет в интервал от 7,749 до 9,039 тыс. руб. 13. Проверить построенное уравнение на наличие мультиколлинеарности по: критерию Стьюдента; критерию χ2. Сравнить полученные результаты. Для проверки построенного уравнения множественного уравнения регрессии на мультиколлинеарность необходимо определить коэффициент парной корреляции между объясняющими переменными (расчеты коэффициента см. выше): Проверка существенности отличия коэффициента корреляции от нуля (значимости) проводится по схеме: если 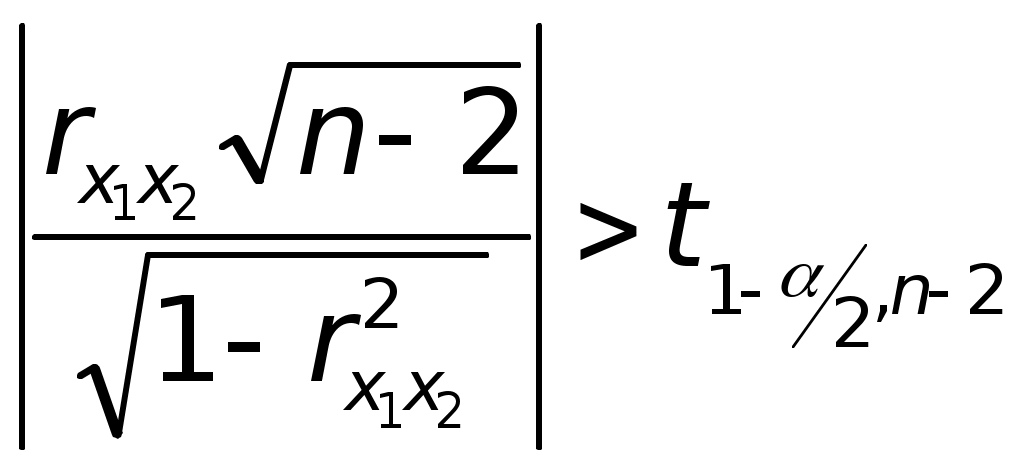 , ,то гипотеза о существенном отличии коэффициента корреляции от нуля принимается, в противном случае – отвергается. Здесь 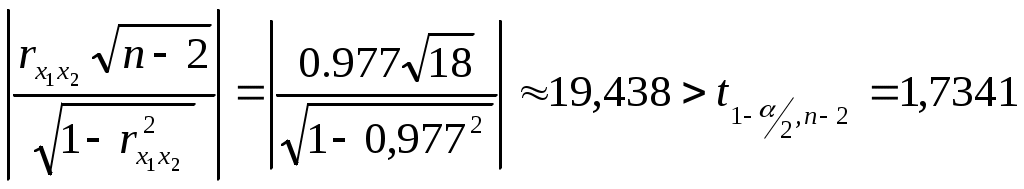 Следовательно, коэффициент корреляции существенно отличается от нуля и существует линейная связь между Проверим гипотезу о независимости объясняющих переменных с помощью критерия «хи-квадрат»: Рассчитаем определитель матрицы коэффициентов парной корреляции: 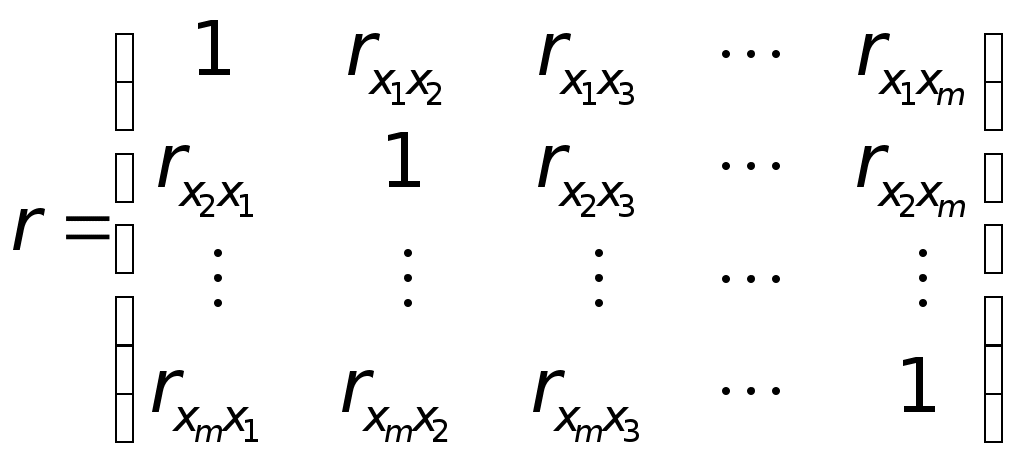 Для данной задачи: Фактическое значение статистики «хи-квадрат»: где Число степеней свободы: Получаем: Табличное значение статистики для Следовательно, можно сделать вывод о наличии мультиколлинеарности. Ситуационная (практическая) задача №2 Имеются помесячные данные по объему платных услуг населению в 2010 г. 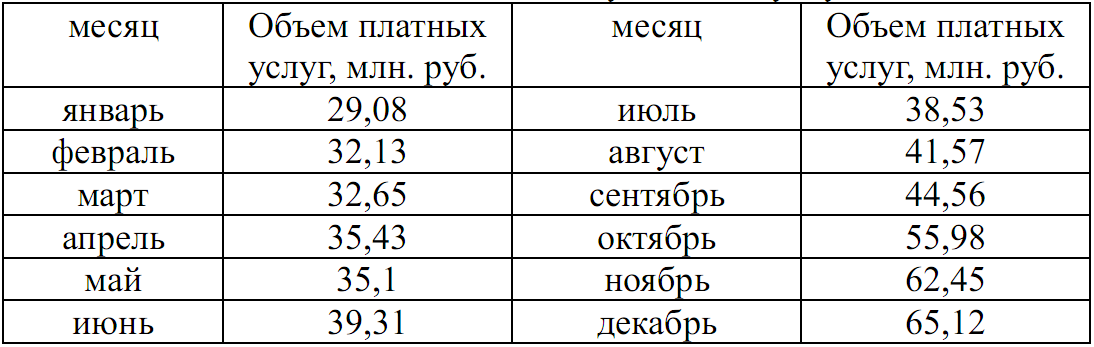 Требуется: 1. Проверить гипотезу о наличии тренда во временном ряде. 2. Рассчитать коэффициенты автокорреляции. Проверить наличие сезонных колебаний во временном ряде. 3. Оценить параметры линейной трендовой модели, проверить статистическую значимость соответствующего уравнения регрессии с надежностью 0,99. 4. Дать точечный и интервальный прогноз объема платных услуг на февраль 2011 г. с надежностью 0,99. 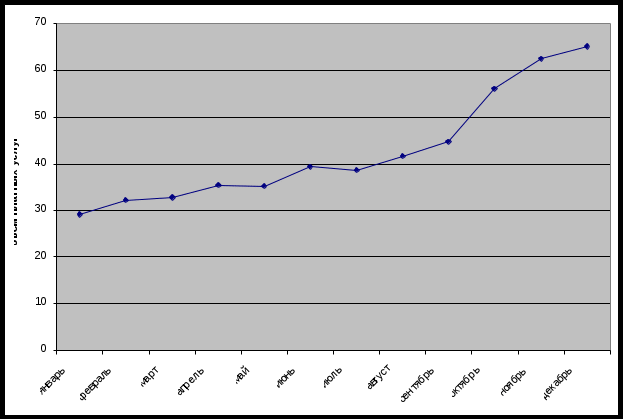 Рис.1 Количественное измерение корреляции осуществляется посредством использования линейного коэффициента корреляции между уровнями исходного временного ряда и уровнями этого ряда, сдвинутыми на несколько шагов во времени: 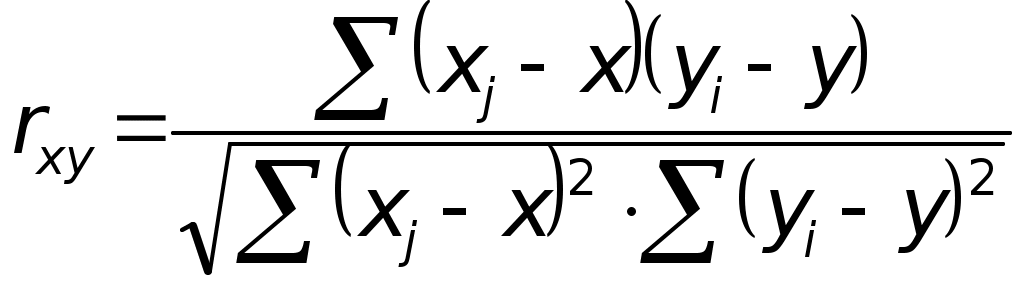 Если сдвиг во времени составляет всего один шаг, то соответствующий коэффициент корреляции называется коэффициентом автокорреляции уровней ряда первого порядка. При этом лаг равен 1. Измеряется же зависимость между соседними уровнями ряда. В общем случае число шагов (или циклов), на которые осуществляется сдвиг, характеризующий влияние запаздывания, также называется лагом. С увеличением лага число пар значений, по которым рассчитывается коэффициент автокорреляции, уменьшается. Таблица 2. Расчетная таблица для определения коэффициента автокорреляции
Получаем: 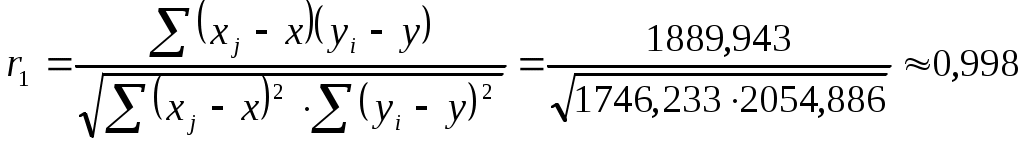 Так как коэффициент автокорреляции первого порядка оказался высоким, то исследуемый ряд содержит только 1 2 |
