РГР. Задача 1 Расчёт идеального компрессора
 Скачать 0.99 Mb. Скачать 0.99 Mb.
|
|
Задача №1 Расчёт идеального компрессора. В одноступенчатом идеальном компрессоре сжимается идеальный газ, имеющий начальное избыточное давление р1ман , кПа, температуру t1, 0С и подается потребителю в количестве М, кг/с (массовый расход) под избыточным давлением р2ман. Определить температуру газа в конце сжатия, плотность в начале и в конце сжатия при изотермическом, адиабатическом и политропном (показатель политропы n) процессах сжатия. Сравнить теоретические мощности, затрачиваемые на привод компрессора; количество выделяемой теплоты в каждом из указанных процессов сжатия. Изобразить процессы сжатия в p-v и T-∆s координатах с учетом масштаба. Дано: t1 = 287 К р1ман = 0,01 МПа р1 = 0,01+0,1=0,11 МПа n = 1,30 газ Кислород О2 k = 1,4 RО2 = 259,8 Дж/кг*К M = 0,29 кг/с р2ман = 0,170 МПа р2 = 0,170+0,1=0,270 МПа Решение: 1) Определение термических параметров состояния в характерных точках рабочего цикла компрессора 1.1) Абсолютная температура газа после сжатия Адиабатический процесс: 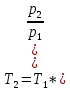 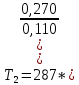 Политропный процесс: 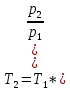 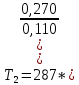 Изотермический процесс: 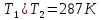 1.2) Плотность газа В начале сжатия: 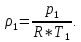 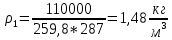 В конце адиабатического сжатия: 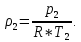 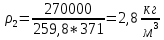 В конце политропного сжатия: 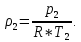 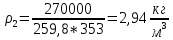 В конце изотермического сжатия: 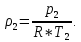 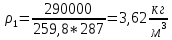 2) Определение энергетических параметров работы компрессора 2.1) Определение удельных затрат механической энергии (работы) на привод компрессора При адиабатическом сжатии: 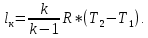 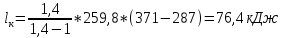 При политропном сжатии: 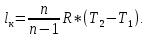 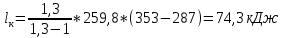 При изотермическом сжатии: 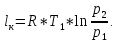 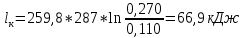 2.2) Определение теоретической мощности привода компрессора: 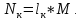 Для адиабатического сжатия: 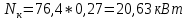 Для политропного сжатия: 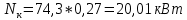 Для изотермического сжатия: 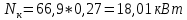 3) Определение теплоты, отводимой от газа в процессе сжатия 3.1) Удельная теплота для изотермического процесса: 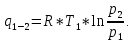 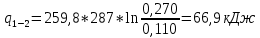 3.2) Вся теплота с учетом массового расхода для изотермического процесса: 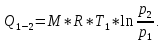 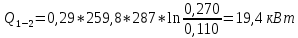 3.3) Удельная теплота для политропного процесса: 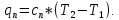 где cn - удельная массовая теплоемкость политропного процесса: 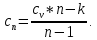 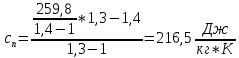 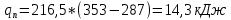 3.4) Вся теплота с учетом массового расхода для политропного процесса: 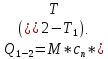 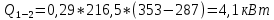 Таблица 1 - Результаты расчетов энергетических характеристик компрессоров
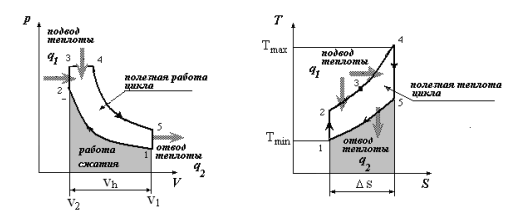
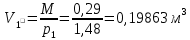 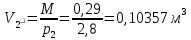 (адиабатическое сжатие) (адиабатическое сжатие)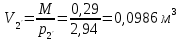 (политропное сжатие) (политропное сжатие)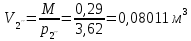 (изотерическое сжатие) (изотерическое сжатие) 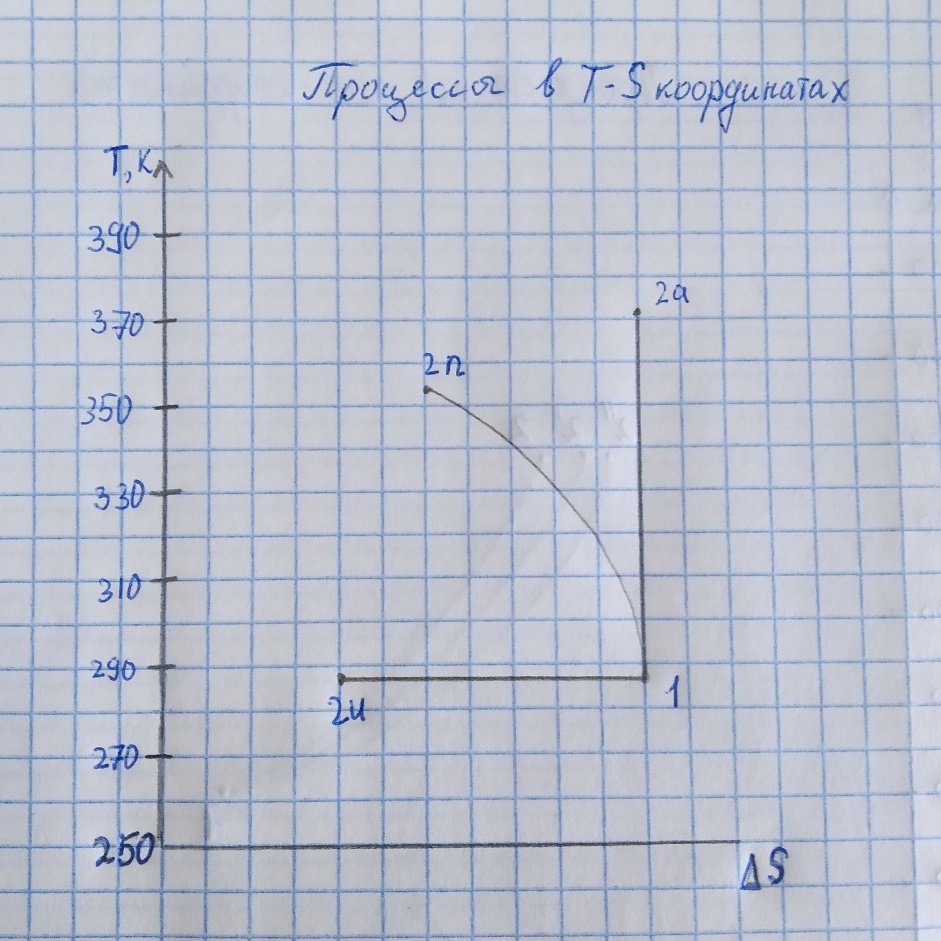 1 – начало процесса, 2и – конец изотермического процесса, 2а – конец адиабатического процесса, 2п – конец политропного процесса Выводы: Расчет параметров процесса сжатия водорода в компрессоре показал, что с ростом показателя политропы (от 1 до 1,9) увеличиваются такие характеристики как конечная температура, мощность привода, все максимальные значения получены для политропного процесса при n=1,3<1,4. Плотность газа в конце процесса, напротив, убывает с ростом показателя политропы (максимальное значение в конце изотермического процесса 2,57 кг/м3 и минимальное в конце политропного 1,46 кг/м3) Задача №2 Расчёт идеального прямого термодинамического цикла. Для идеального термодинамического цикла теплового двигателя определить параметры состояния рабочего тела в характерных точках, удельную работу расширения каждого процесса (для 1 кг рабочего тела), изменение внутренней энергии и энтальпии каждого процесса, термический КПД цикла, среднее давление цикла, удельную теоретическую литровую (для 1 л рабочего объема) мощность двигателя. Рабочее тело - идеальный газ со свойствами воздуха (R=287 Дж/(кг.К), k=1,4). Известны параметры в начальной точке: абсолютное давление p1 кПа и температура t1=30˚С, а также степень сжатия ε=16, количество подводимой теплоты на изохорном участке цикла qv=0, количество подводимой теплоты на изобарном участке qр=1,4МДж/кг, частота вращения коленчатого вала n=1500 мин-1. Изобразить цикл в координатных системах «p-v» и «T-∆s» с учетом масштаба. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Вид цикла – Тринклера, ε=14, λ=2,200, ρ=1,445 | |||
| Характерные точки процессов цикла | Абсолютное давление, МПа | Абсолютная температура, К | Удельный объём, м3/кг |
| 1 | 0,099 | 283 | 0,820 |
| 2 | 3,983 | 813 | 0,059 |
| 3 | 8,763 | 1789 | 0,059 |
| 4 | 8,763 | 2585 | 0,085 |
| 5 | 0,365 | 1042 | 0,820 |
Расчет энергетических характеристик
Процесс 1-2 (сжатие):
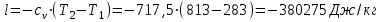 .
.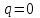 .
.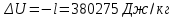 .
.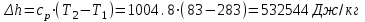 .
.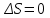 .
.Процесс 2-3 (подвод теплоты по изохоре):
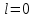 .
.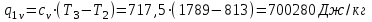 .
.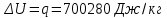 .
.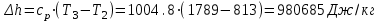 .
.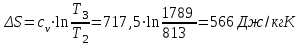 .
.Процесс 3-4 (подвод теплоты по изобаре):
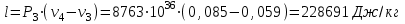 .
.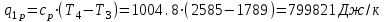 .
.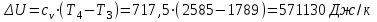 .
.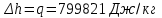 .
.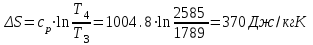 .
.Процесс 4-5 (расширение):
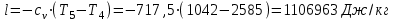 .
.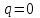 .
.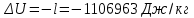 .
.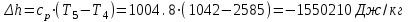 .
.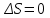 .
.Процесс 5-1 (отвод теплоты):
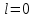 .
.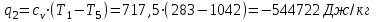 .
.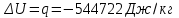 .
.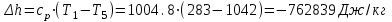 .
.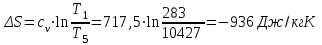 .
.Таблица 3 – Результаты расчетов
| Вид цикла – Тринклер, ε=14, λ=2,200, ρ=1,445 | |||||
| Процесс | Уд. Теплота кДж/кг | Уд. Работа, кДж/кг | Изменение уд. Внутр. Энергии, кДж/кг | Изменение уд. Энтальпии, Дж/кг | Проверка выполнения q=ΔU+l |
| 1-2 | 0 | -380,275 | 380,275 | 0 | 380,275-380,275=0 |
| 2-3 | 700,280 | 0 | 700,280 | 566 | 0+700,2=700,28 |
| 3-4 | 799,821 | 228,691 | 571,130 | 370 | 571,13+228,691=799,821 |
| 4-5 | 0 | 1106,963 | -1106,963 | 0 | 1106,963-1106,963=0 |
| 5-6 | -544,722 | 0 | -544,722 | -935 | -544,722+0=-544,722 |
| Проверка | 955,379 | 955,379 | 0 | 0 | |
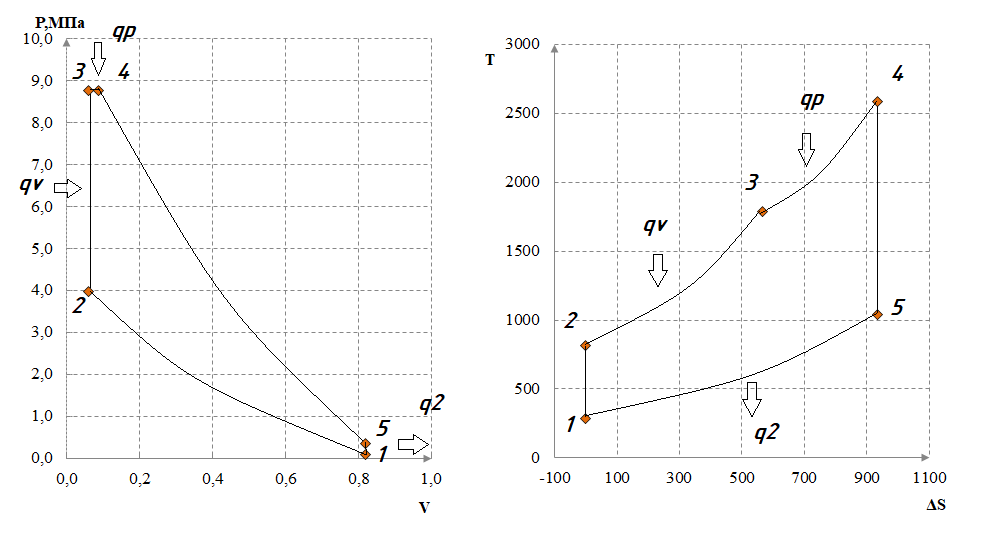
Рисунок 3 – Изображение цикла Тринклера согласно расчетов
Термический КПД:
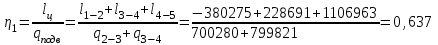
Среднее давление
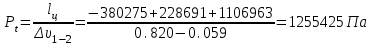
Теоретическая удельная литровая мощность двигателя:
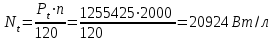
Выводы:
Произведен расчет состояния рабочего тела (воздуха) в характерных точках цикла Тринклера (степень сжатия 14) - температура, давление, удельный объем.
Произведен расчет энергетических характеристик – изменение удельной работы, теплоты, внутренней энергии, энтальпии и энтропии.
Результаты расчетов отражены на графиках.
Среднее давление цикла - 1,26МПа.
Термический ЕПД 0,637.
Теоретическая удельная литровая мощность равна 20,924 кВт/л.
Задача №3
Расчёт теплопередачи через плоскую стенку
Определить величину удельных тепловых потерь за счет конвекции ограждающей конструкции (стен) жилого здания, если на стене толщиной 1 с внутренней стороны имеется слой штукатурки (или дерева) толщиной 2 , под которым размещен слой тепловой изоляции толщиной 3. С наружной стороны стены имеется слои штукатурки такой же толщиной 2.
Известны: коэффициент теплопроводности материала стены 1, коэффициент теплопроводности материала слоя штукатурки или дерева 2, коэффициент теплопроводности слоя тепловой изоляции 3.
Внутри помещения требуется поддерживать температуру воздуха tf1; с наружной стороны стены установилась температура окружающего воздуха tf2.
Коэффициент теплоотдачи с внутренней стороны стены 1=8,7 Вт/(м2К), коэффициент теплоотдачи с внешней (уличной) стороны для зимних условий 2=23 Вт/(м2К) - соответствуют требованиям СНиП 23-02-2003 Свод правил. Тепловая защита зданий.
Рассчитать температуры поверхностей слоев стены. Построить графики изменения температуры по толщине многослойной стенки с учетом масштаба температуры и толщины.
Определить глубину промерзания стены для заданных условий (тепловая изоляция установлена на внутренней поверхности стены.
Дано :
α1 = 8,7 Вт/(м2*К); α2 = 23 Вт/(м2*К).
Материал стены – Монолитный железобетон
δ3 = 0,5 м; λ3 = 1,55 Вт/(м*К);
δ4 = 14 мм = 0,014м; λ4= 0,44 Вт/(м*К);
Штукатурка;
Материал изоляции – Пенополистирол
δ2 = 40 мм = 0,04 м; λ 2= 0,064 Вт/(м*К);
λ 1 =0,18 Вт/(м*К) δ1 =0,018м( дерево сухая сосна)
tf 1= 19°С; tf2 = -30°С;
Решение:
Термическое сопротивление теплопередачи через плоскую трёхслойную стенку:
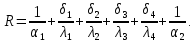
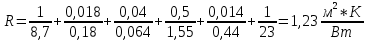
Плотность теплового потока через плоскую четырехслойную стенку:
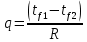
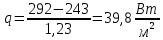
Определение термического сопротивления и плотности теплового потока без изоляции:
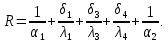
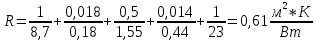
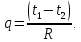
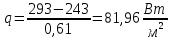
Тепловой поток без изоляции увеличится на
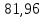 -39,8=42,16 Вт/м2
-39,8=42,16 Вт/м2Температура внутренней и внешней поверхности многослойной стенки и на границе слоев:
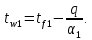
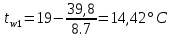
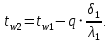
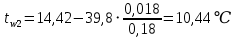
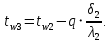
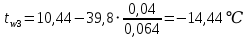
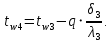
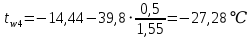
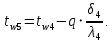
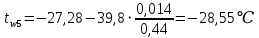
Проверка:
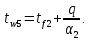
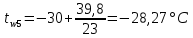
Определение глубины промерзания слоя пенополистирола:
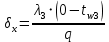
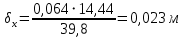
Глубина промерзания стены составит:
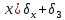
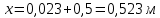
Температура внутренней и внешней поверхности многослойной стенки и на границе слоев без изоляции:
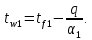
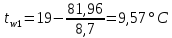
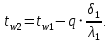
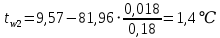
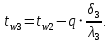
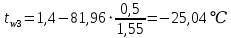
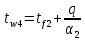
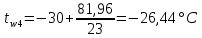
Определение глубины промерзания:
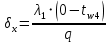
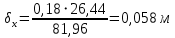
Глубина промерзания стены со штукатуркой (снаружи) составит:
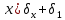
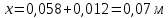
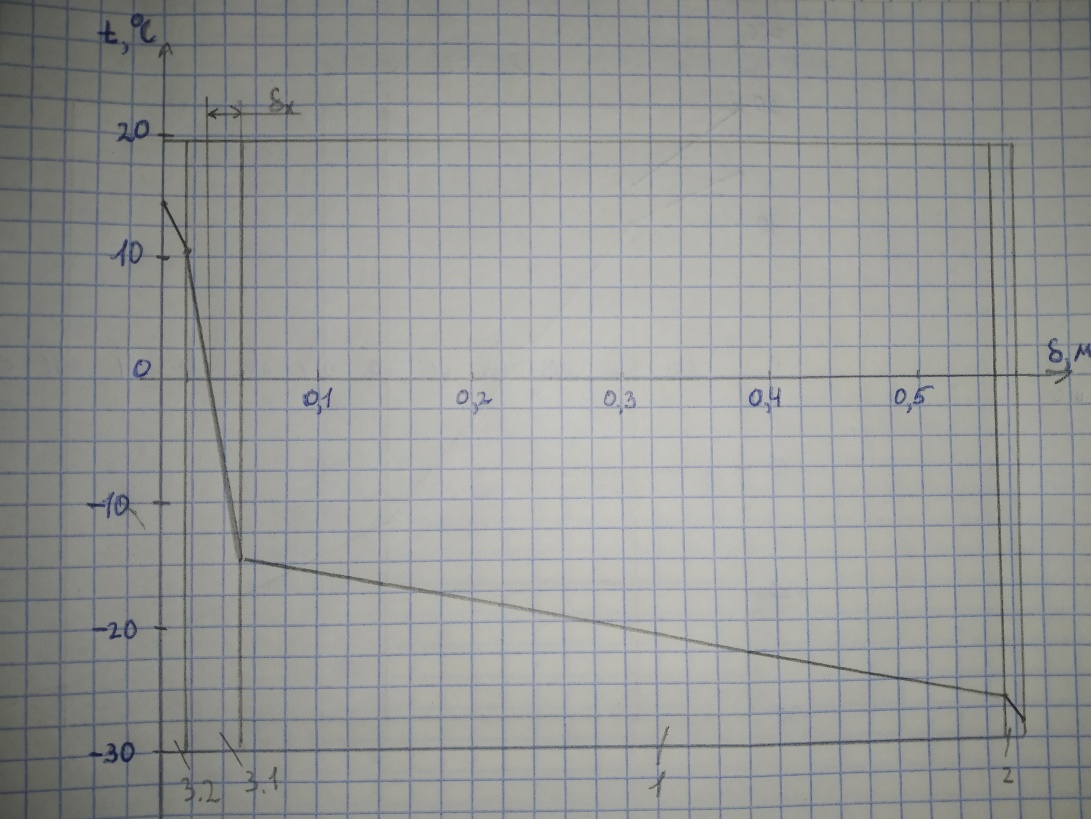
1 – Монолитный железобетон; 2 – штукатурка; 3.1 – пенополистирол; 3.2 – дерево (сухая сосна)
Рисунок 6 – Распределение температуры по толщине четырехслойной плоской стенки
Выводы:
Удельные тепловые потери через стенку составляют
 Вт/м2.
Вт/м2.Рассчитаны температуры на границе слоев и на поверхностях стены. Построен график в масштабе.
Глубина промерзания стены 0,523 м.
Задача 4
Расчёт теплопередачи через цилиндрическую стенку
Внутри трубы с внутренним диаметром d1 и толщиной стенки δ1, изготовленной из материала с коэффициентом теплопроводности λ1, имеющей на внутренней поверхности слой накипи толщиной δ0 с коэффициентом теплопроводности λ0 , движется горячая вода со скоростью w1, имеющая среднюю температуру tf1.
Наружная поверхность покрыта слоем материала толщиной δ2 с известным коэффициентом теплопроводности λ2 и находится в воздухе, имеющем температуру tf2 при отсутствии вынужденного движения. Известна степень черноты наружной поверхности ε.
Определить:
1 Линейную плотность теплового потока (тепловые потери с 1 м длины), передаваемого в воздух с наружной поверхности за счет свободной конвекции.
2 Критический диаметр изоляции (внешнего слоя); сделать вывод об эффективности наружного слоя как тепловой изоляции.
3 Температуры: на поверхности накипи со стороны воды; на внутренней и наружной поверхности стенки трубы; на наружной поверхности внешнего слоя (изоляции). Построить график изменения температуры по толщине многослойной цилиндрической стенки для условий задачи в масштабе.
4 Линейную плотность теплового потока (тепловые потери с 1 м длины), передаваемого в воздух за счет излучения наружной поверхности трубы.
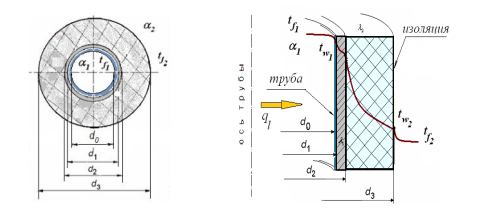
Рисунок 8 – Схема многослойной цилиндрической трубы
Дано:
Таблица 1 – Исходные данные
| d1, мм | δ0, мм | δ1, мм | δ2, мм | λ0, Вт/мК | λ1 Вт/мК | λ2, Вт/мК | w1, м/с | tf1, ºС | tf2, ºС | ε |
| 18 | 0,6 | 0,8 | 15 | 1,8 | 30 | 0,055 | 1,8 | 70 | 15 | 0,85 |
Материал трубы – Алюминиевый сплав, материал наружного покрытия трубы – Минер вата
Таблица 2 – Теплофизические свойства теплоносителей
| № | Теплофизические свойства среды | Единицы измерения | Вода при средней температуре | Воздух при средней температуре |
| 1 | Коэффициент теплопроводности, | Вт/м*К | 0,680 | 0,0263 |
| 2 | Коэффициент кинематической вязкости, 106 | м2/с | 0,415 | 14,61 |
| 3 | Число Прандтля (Pr) при средней температуре среды (tf) | - | 2,55 | 0,704 |
| 4 | Число Прандтля (Pr) при средней температуре стенки (tw) | - | 2,98 | 0,702 |
Решение:
Определение коэффициента теплоотдачи при вынужденном течении воды внутри трубы.
Критерий Рейнольдса:
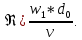
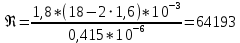
Критерий Нуссельта:
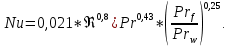
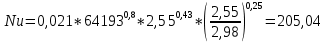
Коэффициент теплоотдачи при вынужденном течении воды внутри трубы:
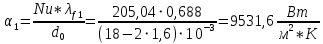
Определение коэффициента теплоотдачи в воздух с внешней стороны трубы при свободной конвекции с изоляцией.
Критерий Грасгофа:
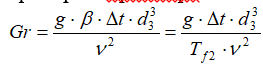
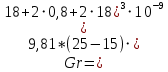
Критерий Нуссельта:
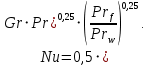
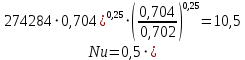
Коэффициент теплоотдачи в воздух с внешней стороны трубы при свободной конвекции:
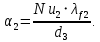
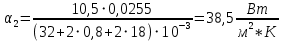
Определение суммарного термического сопротивления и коэффициента теплопередачи.
Линейное термическое сопротивление внутри трубы:
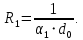
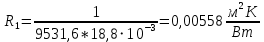
Линейное термическое сопротивление слоя накипи:
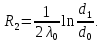
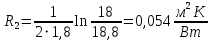
Линейное термическое сопротивление стенки трубы:
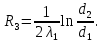
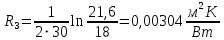
Линейное термическое сопротивление слоя изоляции:
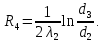
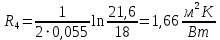
Линейное термическое сопротивление на границе:
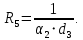
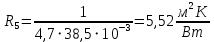
Суммарное линейное термическое сопротивление трубы:

Линейный коэффициент теплопередачи:
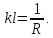
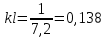
Тепловые потери за счет вынужденной конвекции:
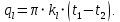
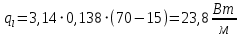
Критический диаметр изоляции:
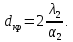
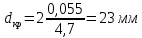 <21,6
<21,6Условие эффективной работы изоляции не выполняется
Расчет температур.
На внутренней поверхности со стороны воды:
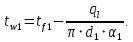
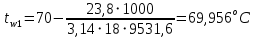
На внутренней поверхности трубы под накипью:
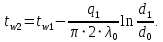
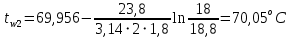
На наружной поверхности трубы под изоляцией:
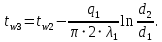
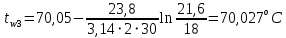
На наружной поверхности трубы с изоляцией:
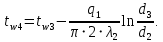
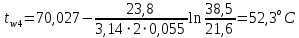
Проверка:
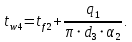
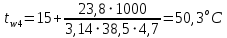
Определение тепловых потерь за счет излучения с наружной поверхности
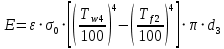
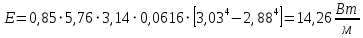

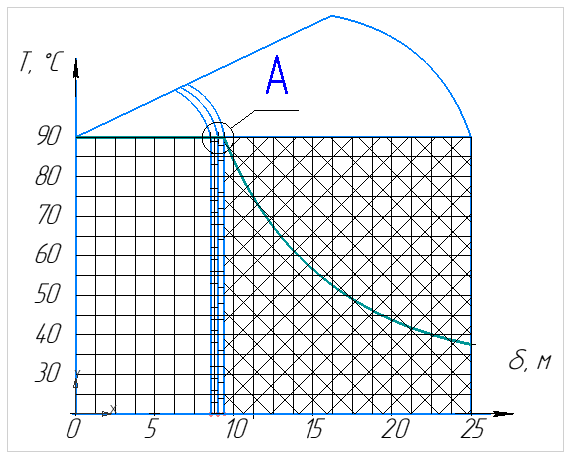
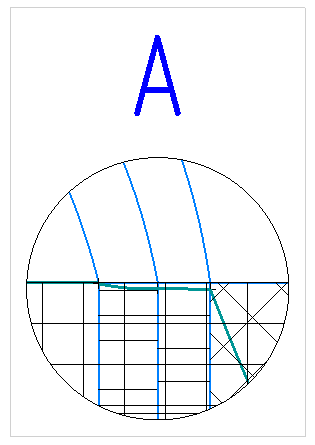
Рисунок 9 – График распределения температур по толщине трехслойной цилиндрической стенки
Выводы:
Изоляция работает эффективно, так как критический диаметр dкр = 11,2 мм не превышает наружный диаметр трубы без изоляции d2 = 19,6 мм.
Линейная плотность теплового потока, передаваемая в воздух за счет излучения наружной поверхности, составляет 8,94 Вт/м.

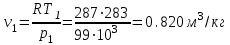 .
.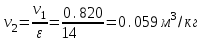 .
.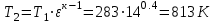 .
.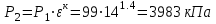 .
. .
.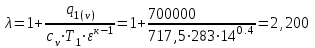 .
.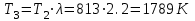
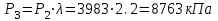 .
.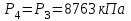 .
.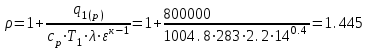 .
.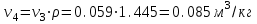 .
.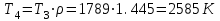 .
.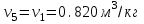 .
.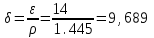 .
.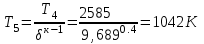 .
.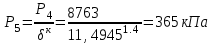 .
.