Задачи по сопромату. Задачи 1,3,4,5,6(1,2). Задача 1 Расчет на прочность и жесткость
 Скачать 2.35 Mb.
|
|
Задача 1 Расчет на прочность и жесткость при растяжении и сжатии Для стержневой системы (рисунок 1) требуется: 1) определить усилия в стержнях; 2) найти площади поперечных сечений в стержнях из расчета на прочность по допускаемым напряжениям; 3) вычислить деформации стержней и перемещение узла В. Размеры конструкции и величины нагрузок приведены в таблице 5. Материал стержней – Сталь 3 со следующими механическими характеристиками: σт = 240 МПа; nт = 1,5; Е = 2 105 МПа. Заштрихованные элементы на схемах считать абсолютно жесткими. Таблица 1 Исходные данные
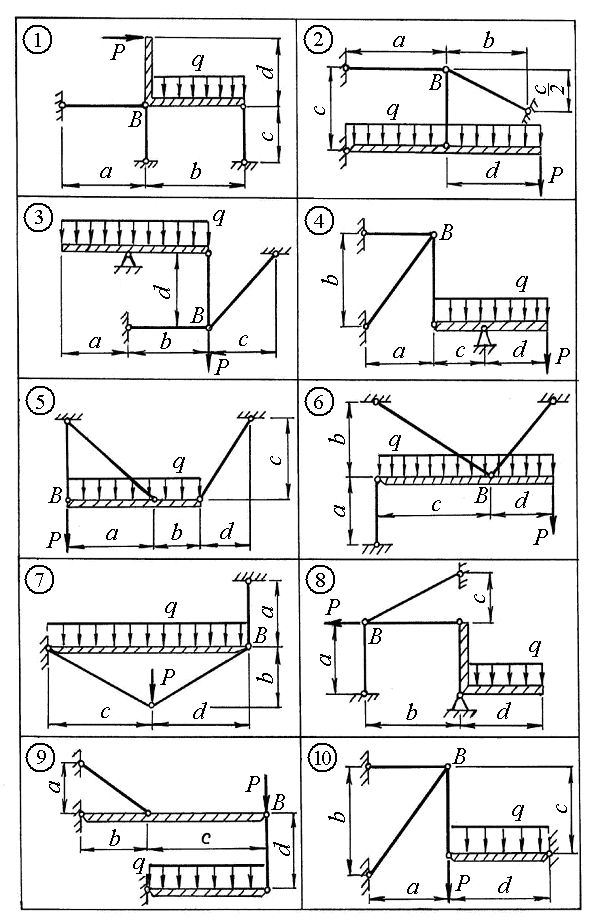 Рис.1. Исходная схема согласно варианту Пример решения задачи 1 Схема стержневой системы показана на рисунке 2. Размеры конструкции и величины нагрузок: a = 1 м; b = 1,2 м; c = 0,8 м; P = 50 кН; q = 20 кН/м. 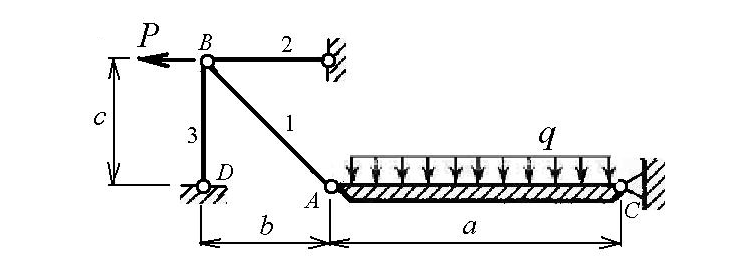 Рисунок 2 Решение. Покажем усилия, действующие в элементах рассматриваемой конструкции. Для этого рассечем систему по стержню AB на две части, как показано на рисунке 3. Распределенную нагрузку заменим равнодействующей qa, приложенной в середине жесткого бруса AC(рисунок 3 а). Усилия в стержнях N1, N2 и N3 направим растягивающими. 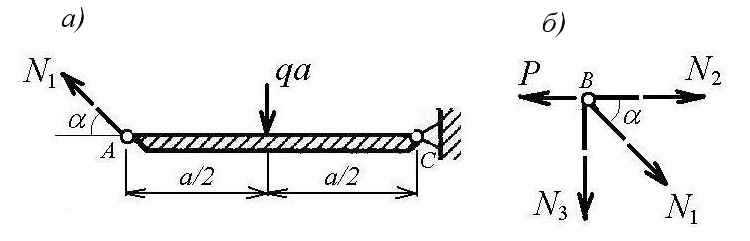 Рисунок 3 Угол наклона стержня AB к горизонтальной оси обозначим  (рисунок 3 а), его синус и косинус равны ; .Для нахождения усилия N1 составим уравнение равновесия, выражающее равенство нулю суммы моментов всех сил, показанных на рисунке 3 а, относительно шарнира С:  ,откуда получим  (кН).Для схемы на рисунке 3 б составим два других уравнения, выражающих суммы проекций на горизонталь и вертикаль соответственно:  Решая систему последних уравнений, получим  (кН), (кН).Знаки полученных усилий указывают на то, что первый и второй стержень испытывают растяжение, а третий – сжатие. Запишем для каждого стержня условие прочности:  ,где допускаемое напряжение равно  (МПа).Таким образом, требуемые площади поперечных сечений равны:  (м2) = 1,125 (см2), (м2) = 2,19 (см2), (м2) = 0,625 (см2).Окончательно принимаем минимально допустимые площади сечений элементов конструкции: F1 = 1,125 см2; F2 = 2,19 см2;F3 = 0,625 см2. Определим абсолютные деформации по формуле  ,где длины стержней  согласно схеме на рисунке 2 составляют  м, l2 = b = 1,2 м, l3 = c = 0,8 м; (м) = 1,15 (мм), (м) = 0,96 (мм), (м) = –0,64 (мм).Если вычислить величины относительных деформаций стержней, то они будут одинаковыми:  .Перемещение узла B можно определить геометрически, связав его с величинами абсолютных деформаций второго и третьего стержней. Чтобы найти положение узла B после деформации, составим план перемещений вблизи этого узла (рисунок 4). 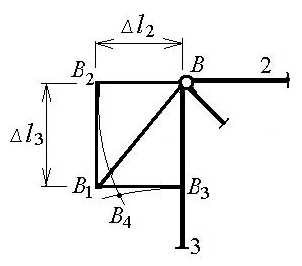 Рисунок 4 Искомое перемещение ΔB равно длине отрезка BB1:  Выводы. 1. Из условий равновесия найдены усилия в стержнях: N1 = 18 кН, N2 = 35 кН,N3 = – 10 кН. При этом стержни 1, 2 испытывают растяжение, стержень 3 – сжатие. 2. Из условий прочности определены площади сечений стержней: F1 = 1,125 см2; F2 = 2,19 см2;F3 = 0,625 см2. 3. При найденных площадях сечений абсолютные деформации стержней составили:  = 1,15 мм,  = 0,96 мм,  = –0,64 мм.Перемещение узла В равно  = 1,15 мм.Задача 3 Расчеты на прочность и жесткость при кручении Стальной вал диаметром d (рисунок 5) вращается равномерно с частотой n об/мин. Мощность на ведущем шкиве составляет N кВт. Моменты трения подшипников пренебрежимо малы. Требуется: 1) построить эпюру крутящих моментов (ординаты эпюры выразить в долях от момента М, передаваемого от ведущего шкива); 2) определить из условия прочности допускаемое значение момента М и число оборотов вращения вала n; 3) при найденном значении М построить эпюру углов поворота сечений, считая левый шкив неподвижным, и проверить выполнение условия жесткости вала (при невыполнении условия изменить допускаемые величины момента М и числа оборотов n). Таблица 2 Исходные данные
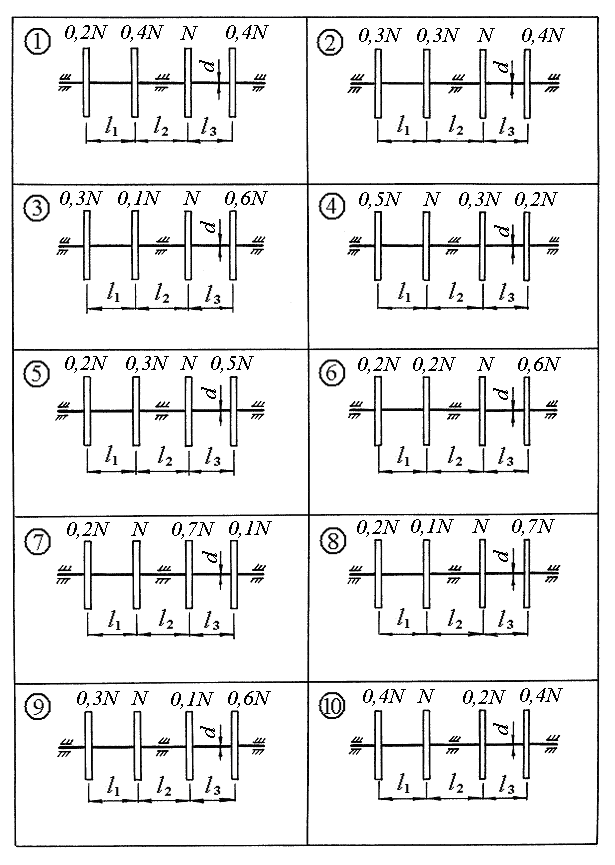 Рис. 5. Исходная схема согласно варианту Пример решения задачи 3 Схема вала показана на рисунке 6. Исходные данные: N = 65 кВт, d = 44 мм, l1 =0,3 м, l2 =0,25 м, l3 =0,2 м, 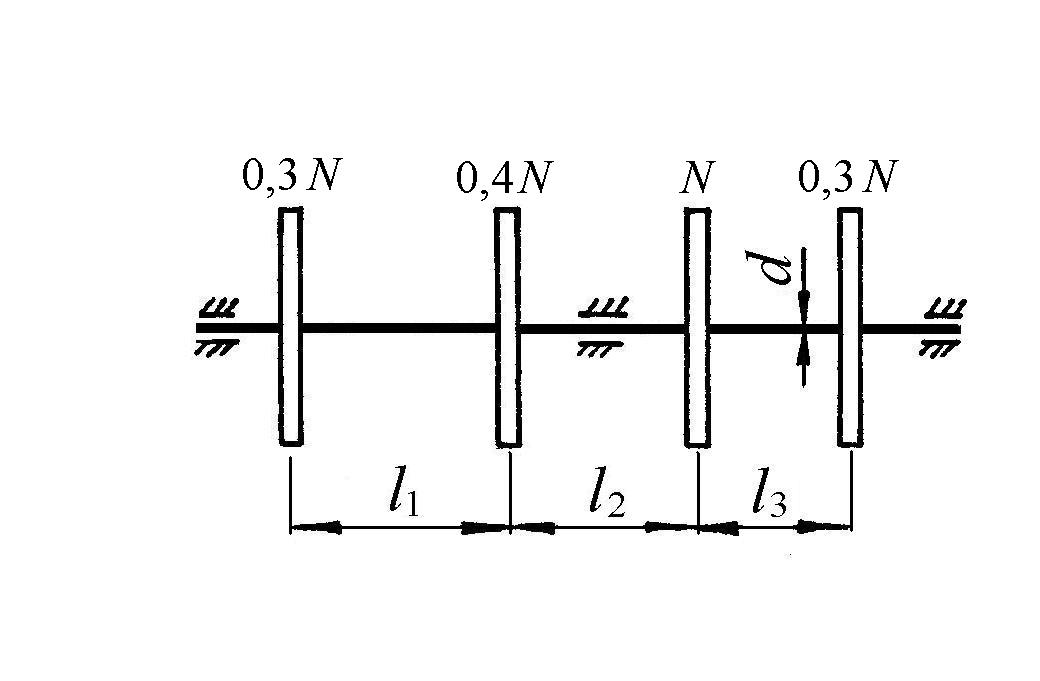 = 50 МПа, [φ] = 0,015 рад. Рисунок 6 Решение. Расчетная схема показана на рисунке 7. Методом сечений, определим крутящие моменты по участкам бруса, выражая их в долях момента М, передаваемого от ведущего шкива: в сечении 1-1: Mк1 = 0,3М ; в сечении 2-2: Mк2 = 0,3М + 0,4М = 0,7М ; в сечении 3-3: Mк3 = 0,3М + 0,4М – М = –0,3М . Эпюра "Mк " показана на рисунке 7 б. Определим из условия прочности допускаемое значение момента М. Поскольку поперечное сечение по всей длине вала одинаково, то наиболее опасным участком является участок 2, где крутящий момент достигает максимальной величины: Mmax = Mк2 = 0,7М . Запишем условие прочности для опасного участка:  ,где 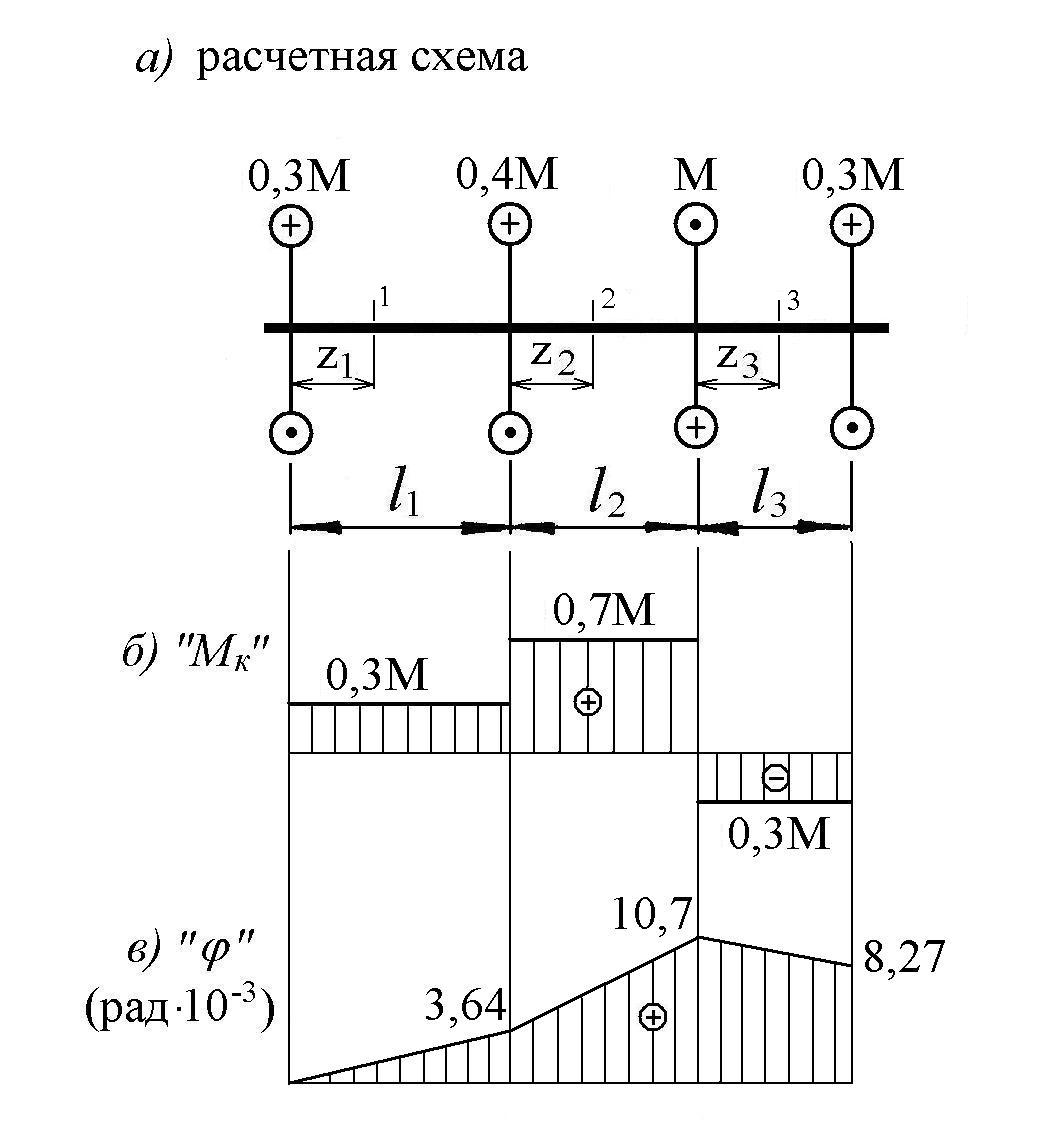 17000 (мм3) =17,0·10–6 (м3). Рисунок 7 Тогда допускаемое значение момента М равно  (Нм).Примем для дальнейших вычислений минимально допускаемый момент М = 1214 Нм. Для вычисления допускаемого числа оборотов вращения вала в минуту n используем зависимость:  ,откуда следует  (об/мин).При найденном значении М вычислим на каждом участке углы поворота сечений, считая левый шкив неподвижным. Координаты  рассматриваемых сечений на каждом из участков вала показаны на рисунке 7 а.Определим жесткость сечения  (Нм2).Угол поворота сечения 1 равен  , здесь  ,вычислим две ординаты в начале и в конце участка:  , (рад).Угол поворота сечения 2 равен  ,  , (рад),  (рад).Угол поворота сечения 3 равен   ,  , (рад),  (рад).Эпюра "φ" показана на рисунке 7 в, откуда видно, что максимальный угол поворота φmax имеет место под ведущим шкивом. Проверим выполнение условия жесткости вала:  (рад),следовательно, условие жесткости удовлетворяется. Выводы. 1. Из построенной эпюры "Mк " установлено, что наиболее опасным участком вала является участок 2, на котором Mmax = 0,7М. 2. Из условия прочности найден допускаемый момент, передаваемый на вал от ведущего шкива, – М = 1214 Нм. При этом допускаемое число оборотов вращения вала составилоn = 511 об/мин. 3. Из построенной эпюры " φ " установлено, что максимальный угол поворота φmax = 0,0107·радиан, что не превышает допускаемого значения 0,015 радиан. Задача 4 Геометрические характеристики плоских сечений Определить величины главных центральных моментов инерции и моментов сопротивления симметричного сечения, составленного из прокатных профилей. Номер схемы по рис. 8 и прочие данные взять из таблицы 3. Таблица 3 Исходные данные
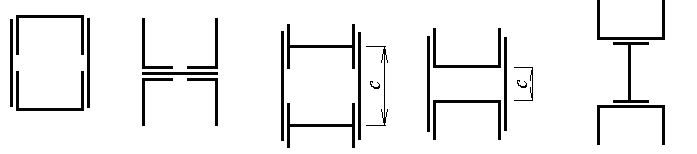 Рис. 8 Исходная схема согласно варианту Пример решения задачи 4 Рассматриваемое сечение составлено двух швеллеров №12 и двух полос 160х10 (мм) (рисунок9). 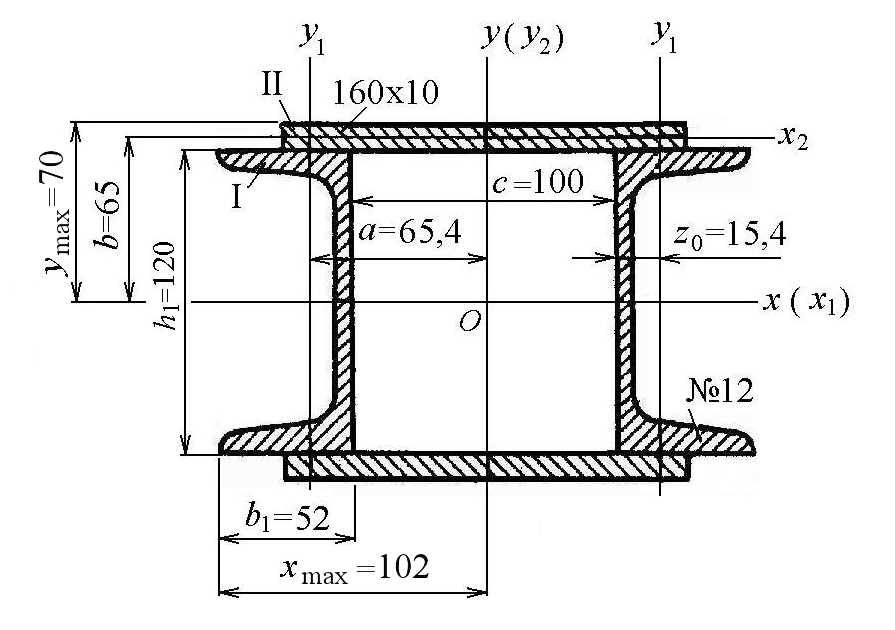 Рисунок 9 Решение. Заданное сечение имеет две оси симметрии, следовательно, положение главных центральных осей очевидно: они совпадают с осями x и y (рисунок 9). Выпишем из таблицы ГОСТ 8240-89 (Приложение А) необходимые данные для швеллера: Jx1 = 304,0 см4; Jy1 = 31,2 см4; F1 = 13,3 см2; h1 = 120 мм; b1 = 52 мм; z0 = 15,4 мм. Вычислим моменты инерции для полосы относительно ее собственных центральных осей  см4;  см4.Площадь сечения полосы равна F2 = 16·1 = 16 см2. Главные центральные моменты инерции всего сечения (индексами "I" и "II" обозначены моменты инерции для швеллера и полосы соответственно) равны   1962,6 см4;  1882,7 см4.Вычислим моменты сопротивления сечения относительно главных центральных осей x и y  ,  ,где  ,  ; ,  .Вывод. Для заданного сечения (рисунок 9) вычислены следующие геометрические характеристики относительно главных центральных осей: моменты инерции –  ;  ;моменты сопротивления –  ;  .Задача 5 Расчет консольной балки при изгибе 1. Для заданной балки построить эпюры поперечных сил Q, изгибающих моментов М, выразив все характерные ординаты через параметры интенсивности распределенной нагрузки "q" и длины "а" (рисунок 10). 2. Из расчета на прочность по допускаемым напряжениям подобрать поперечное сечение балки в виде прямоугольника с отношением сторон h/b= 2, приняв [σ] = 160 МПа. 3. Для подобранной балки определить методом Мора или по правилу Верещагина прогиб и угол поворота на свободном конце. Материал балки – Сталь 3 с модулем упругости Е = 2·105 МПа. Таблица 4 Исходные данные
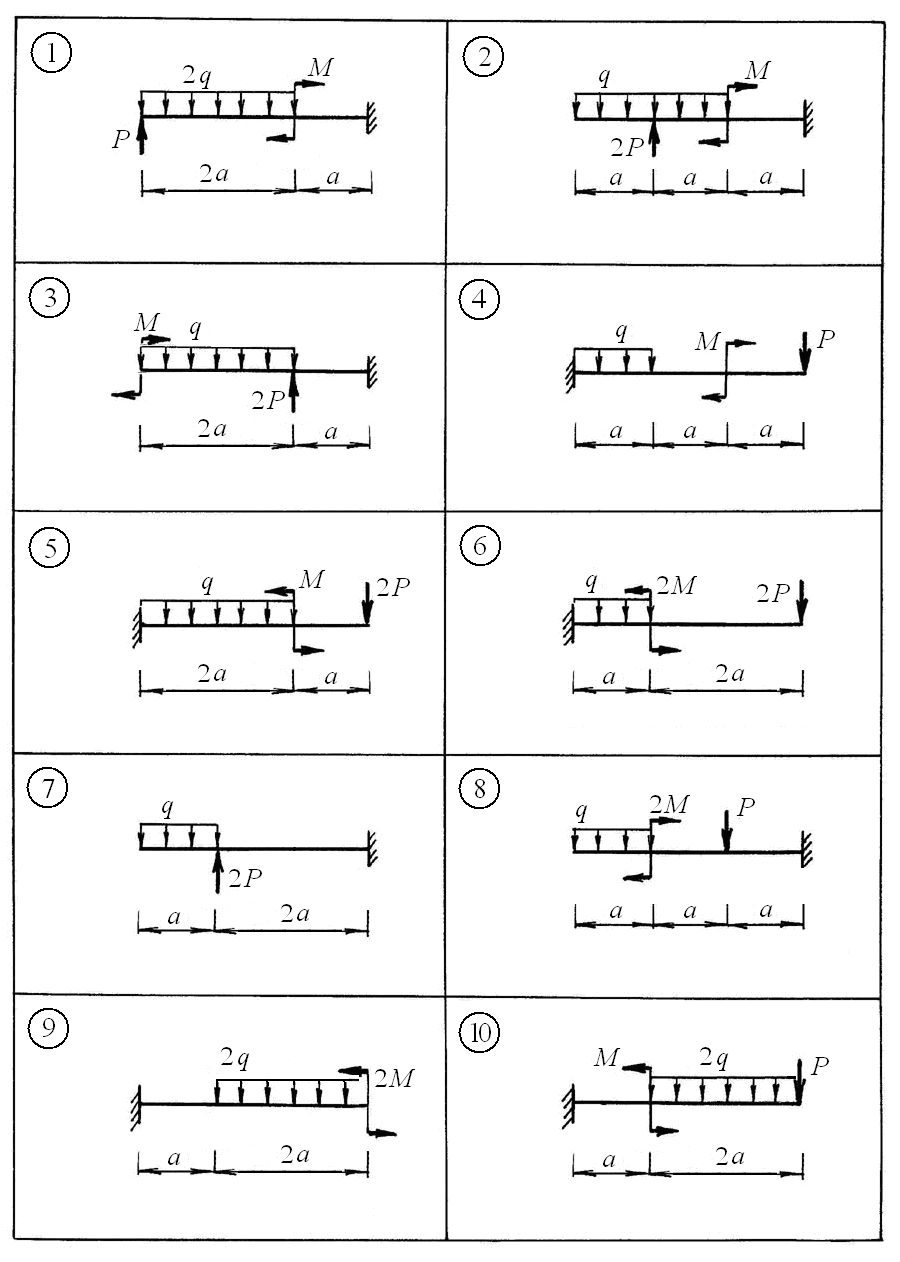 Рис.10 Исходная схема согласно варинту Пример решения задачи 5 Схема балки показана на рисунке 11 а. Исходные данные: q = 40 кН/м; a = 0,5 м; P = qa/2; M = qa2. Решение. Балка имеет два участка. Для построения эпюр Q и М, выполним последовательно два сечения, как показано на рисунке 11 а, рассматривая участки со свободного конца. 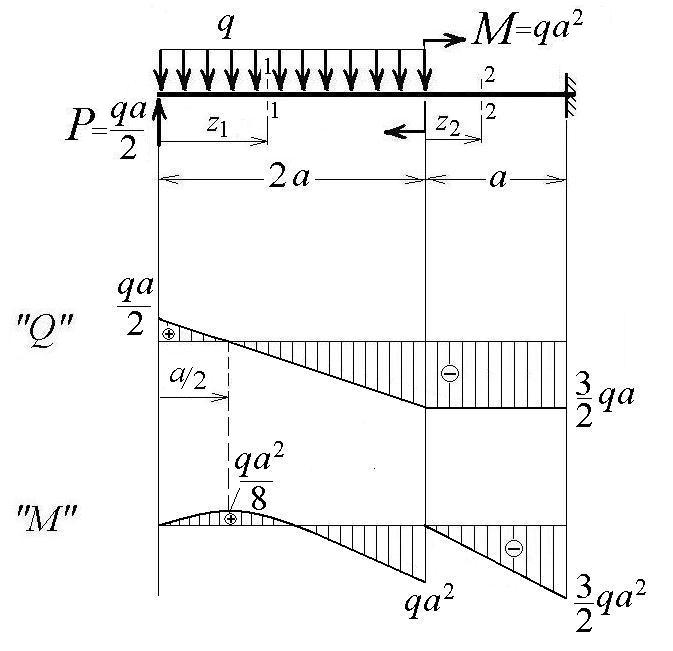 а) г) Сечение 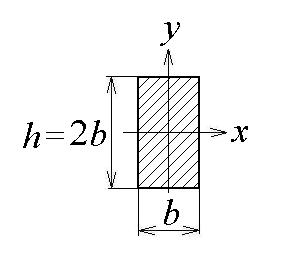 б) в) Рисунок 11 На участке 1 при 0 ≤ z1 ≤ 2a имеем  , .Вычислим характерные ординаты на границах участка:  ,  ; ,  .Поскольку поперечная сила Qна данном участке меняет знак, то определим координату сечения, в котором она равна нулю, и экстремальное значение момента M:  или  , следовательно,  ,тогда  .На участке 2 при 0 ≤ z2 ≤ a получим  ,  .Вычислим характерные ординаты изгибающего момента на границах участка:  ,  .Эпюры Q и М показаны на рисунке 15 б, в. Из эпюры М видно, что опасным является сечение в заделке, в котором величина изгибающего момента максимальна, –  кНм.Условие прочности для балки имеет вид  .Из условия прочности определим требуемый момент сопротивления сечения:  м3.Выразим момент сопротивления прямоугольного сечения через ширину b (рисунок 15 г)  .Найдем требуемые размеры сечения из условия  м3,тогда  м  см.Окончательно принимаем размеры сечения балки b = 5,2 см и h = 2b = 10,4 см. Вычислим прогиб на свободном конце балки графоаналитическим способом, используя на участке 1 формулу Симпсона  ,на участке 2 формулу Симпсона-Корнаухова  ,где Мр и М1 – значения изгибающих моментов от внешних сил и от единичной силы соответственно на левой границе участка (л), на правой границе участка (п) и в середине участка (с). а 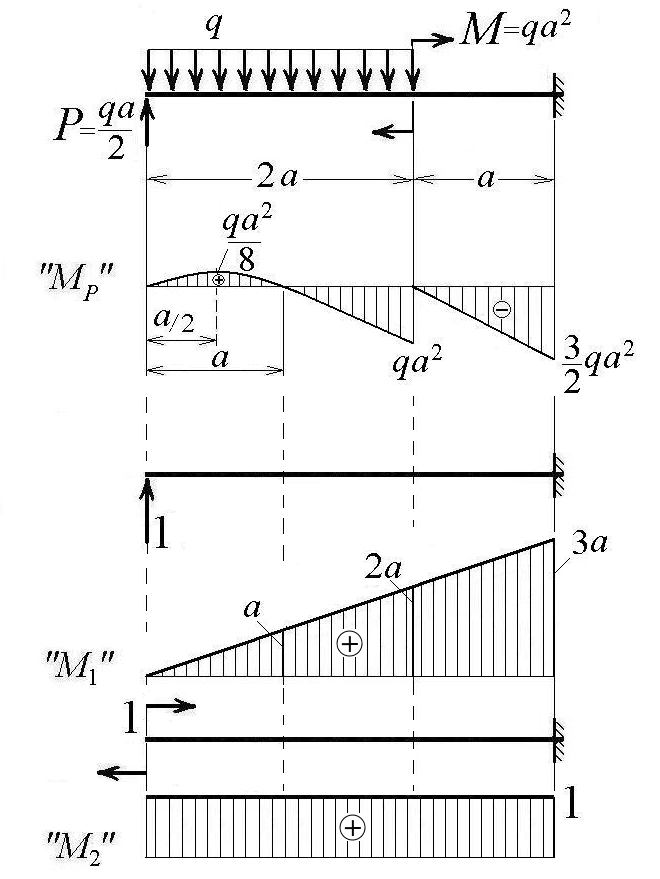 )б) в) г) Рисунок 12 Приложим на свободном конце силу, равную 1, и построим эпюру изгибающего момента М1, как показано на рисунке 12 в. Перемножая эпюру М1 спостроенной ранее эпюрой МР (рисунок 12 б) от заданных нагрузок, получим искомый прогиб:  Знак «минус» показывает, что вычисленный прогиб направлен противоположно единичной силе, то есть вниз. Вычислим момент инерции  сечения балки ,тогда числовое значение прогиба равно  Вычислим угол поворота свободного конца балки, используя тот же метод. Приложим на свободном конце момент, равный 1, и построим эпюру изгибающего момента М2, как показано на рисунке 12 г. Перемножая эпюру М2 спостроенной ранее эпюрой МР (рисунок 12 б) от заданных нагрузок, получим искомый угол поворота:  Знак «минус» показывает, что вычисленный угол поворота направлен противоположно единичному моменту, то есть против часовой стрелки.Числовое значение угла поворота равно  .Выводы. 1. Из построенных эпюр Q и М установлено, что наиболее опасным сечением балки является сечение в заделке, где  ,  .2. Из условия прочности подобраны размеры поперечного сечения балки в виде прямоугольника с размерами b = 5,2 см и h = 10,4 см. 3. Для подобранной балки прогиб свободного конца равен 6,84 мм (направлен вниз), а угол поворота составил 5,56·10-3 радиан (направлен против часовой стрелки). Задача 6 Расчет шарнирной балки при изгибе 1. Для заданной балки построить эпюры поперечных сил Q, изгибающих моментов М, выразив все характерные ординаты через параметры интенсивности распределенной нагрузки "q" и длины "а" (рисунок 13). 2. Из расчета на прочность по допускаемым напряжениям подобрать поперечное сечение балки в виде двутавра, приняв [σ] = 160 МПа. Таблица 5 Исходные данные
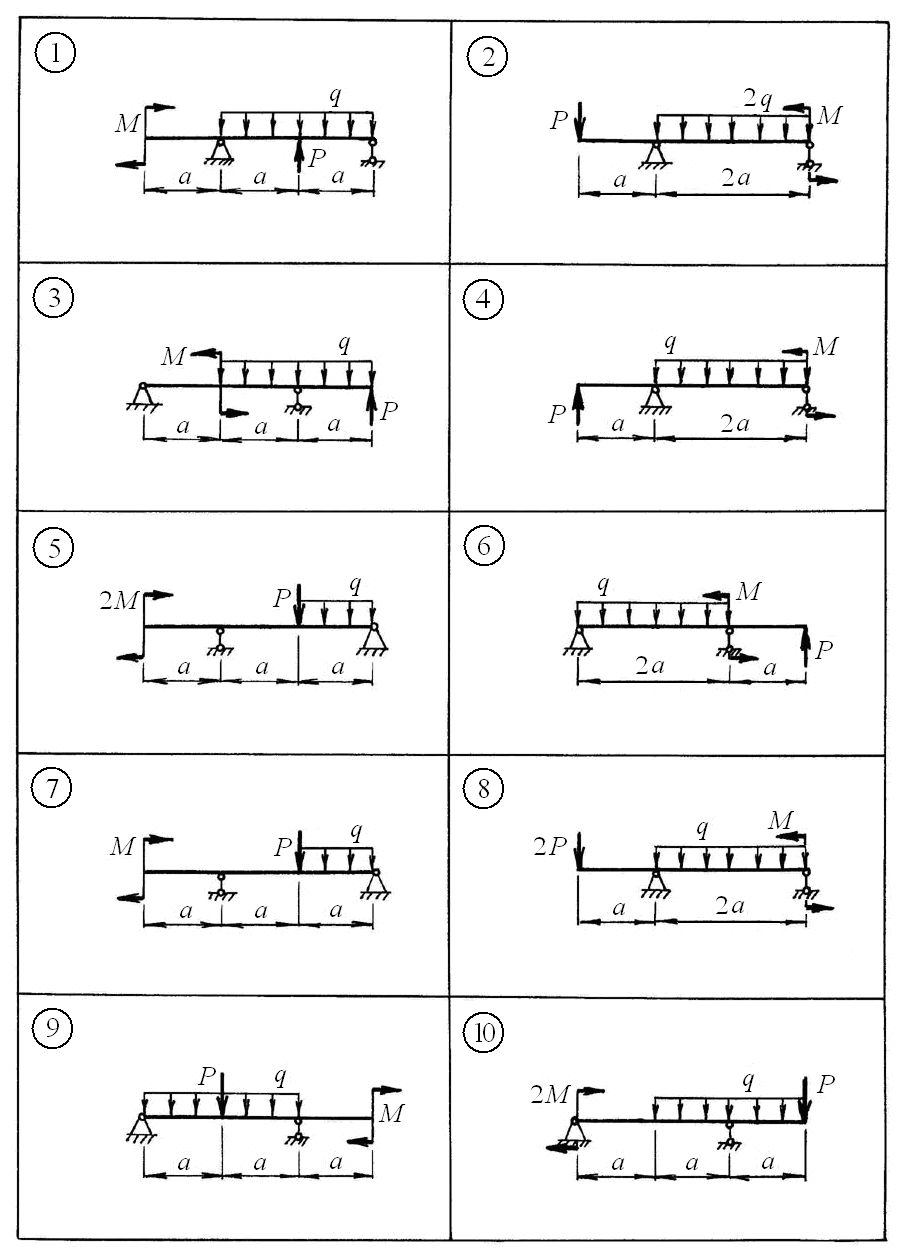 Рисунок 13 Методические указания по выполнению задачи 6 Для выполнения данной задачи рекомендуется следующий порядок решения. 1. Составление выражений для поперечных сил Q, изгибающих моментов Mи построение эпюр: - начертить схему с соблюдением масштаба и нанести на ней значения заданных параметров; - составить уравнения равновесия и вычислить величины опорных реакций, сделать проверку; - составить аналитические выражения внутренних силовых факторов для произвольных сечений по участкам; - вычислить значения внутренних силовых факторов на границах участков и в их характерных сечениях; - проверка правильности построенных эпюр по правилам, вытекающим из дифференциальных зависимостей: 2. Подбор сечения балки: - по эпюре М определить наиболее опасное сечение и вычислить максимальное значение момента Ммах; - определить величину момента сопротивления из условия прочности:  ;- по найденной величине Wx выбрать из таблицы сортамента прокатной стали (Приложение А) соответствующий расчету номер двутавра (при этом в целях экономии расхода материала допускается превышение максимального напряжения в сечении балки по сравнению с величиной допускаемого напряжения не более чем на 5%); - если по найденному расчетному значению Wx невозможно подобрать один прокатный профиль, следует взять два или более одинаковых профиля таких, чтобы сумма их моментов сопротивления удовлетворяла условию прочности. 3. Сделать выводы по решенной задаче. Приложение А. Сортамент      | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||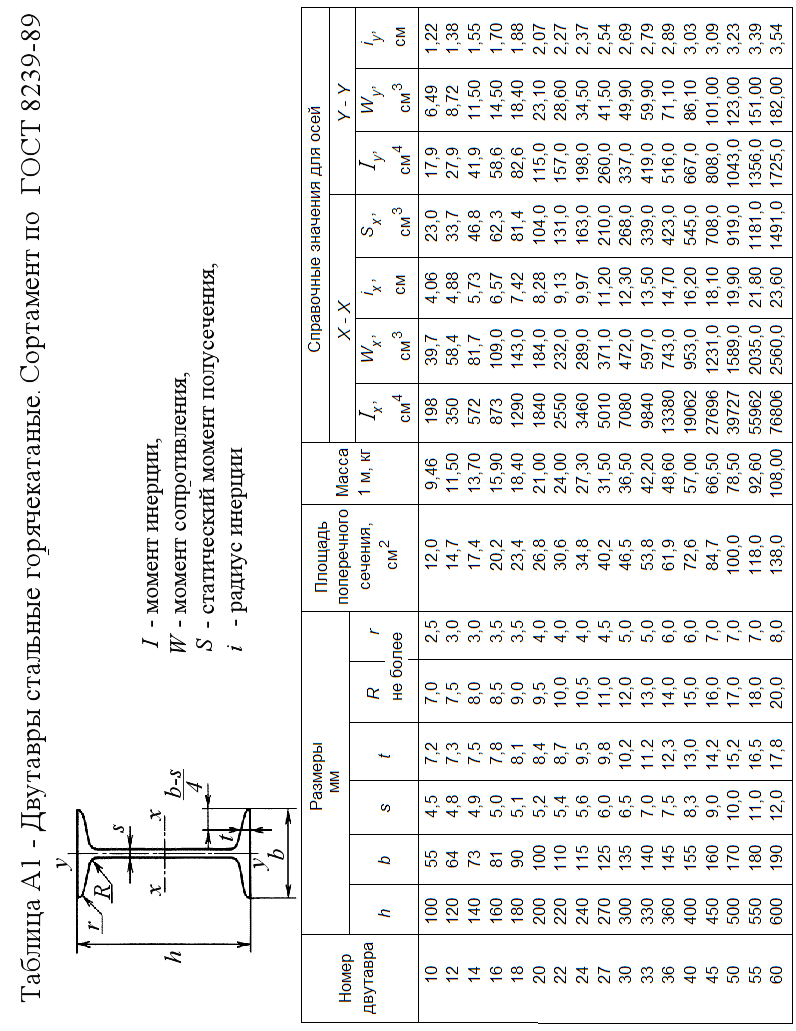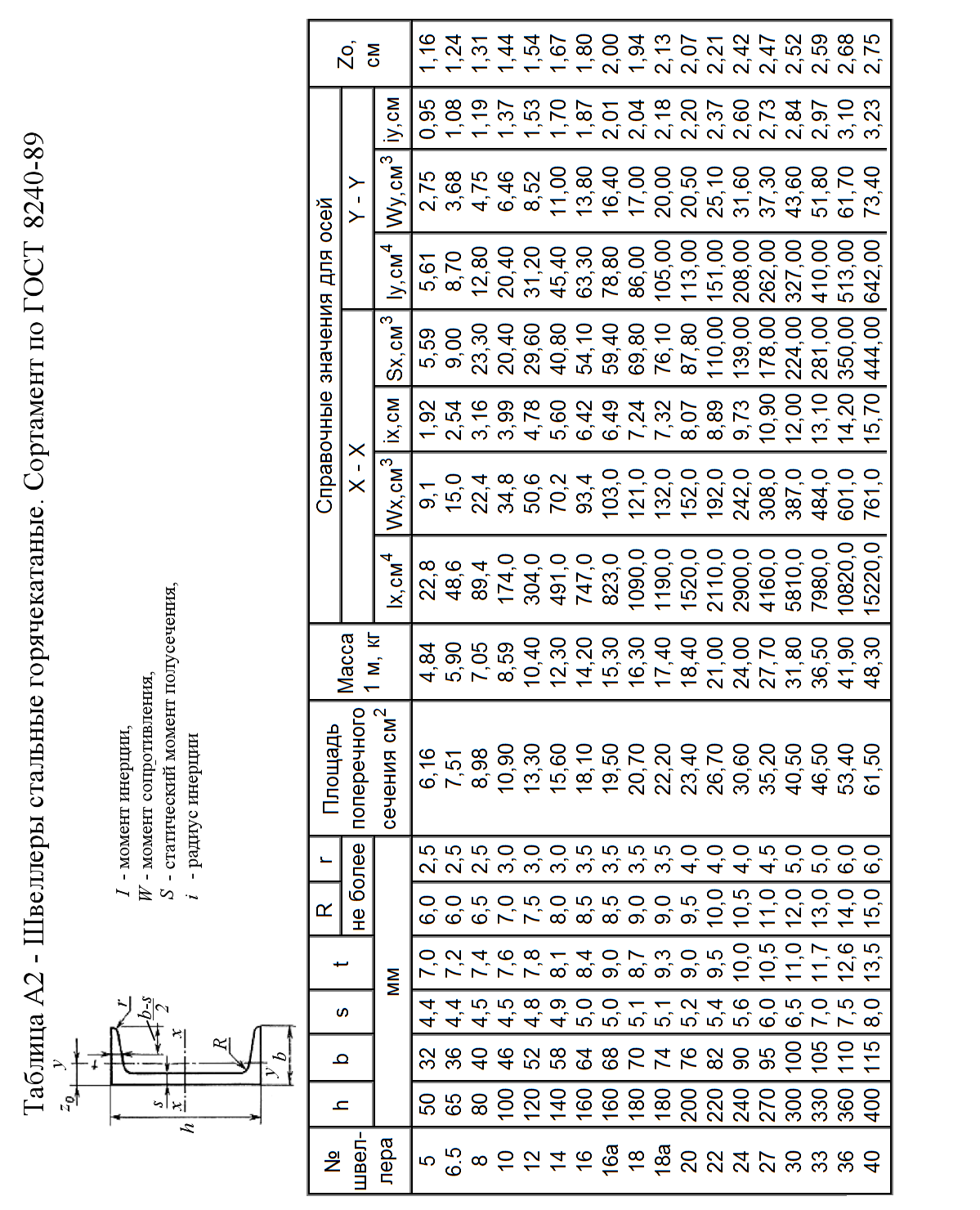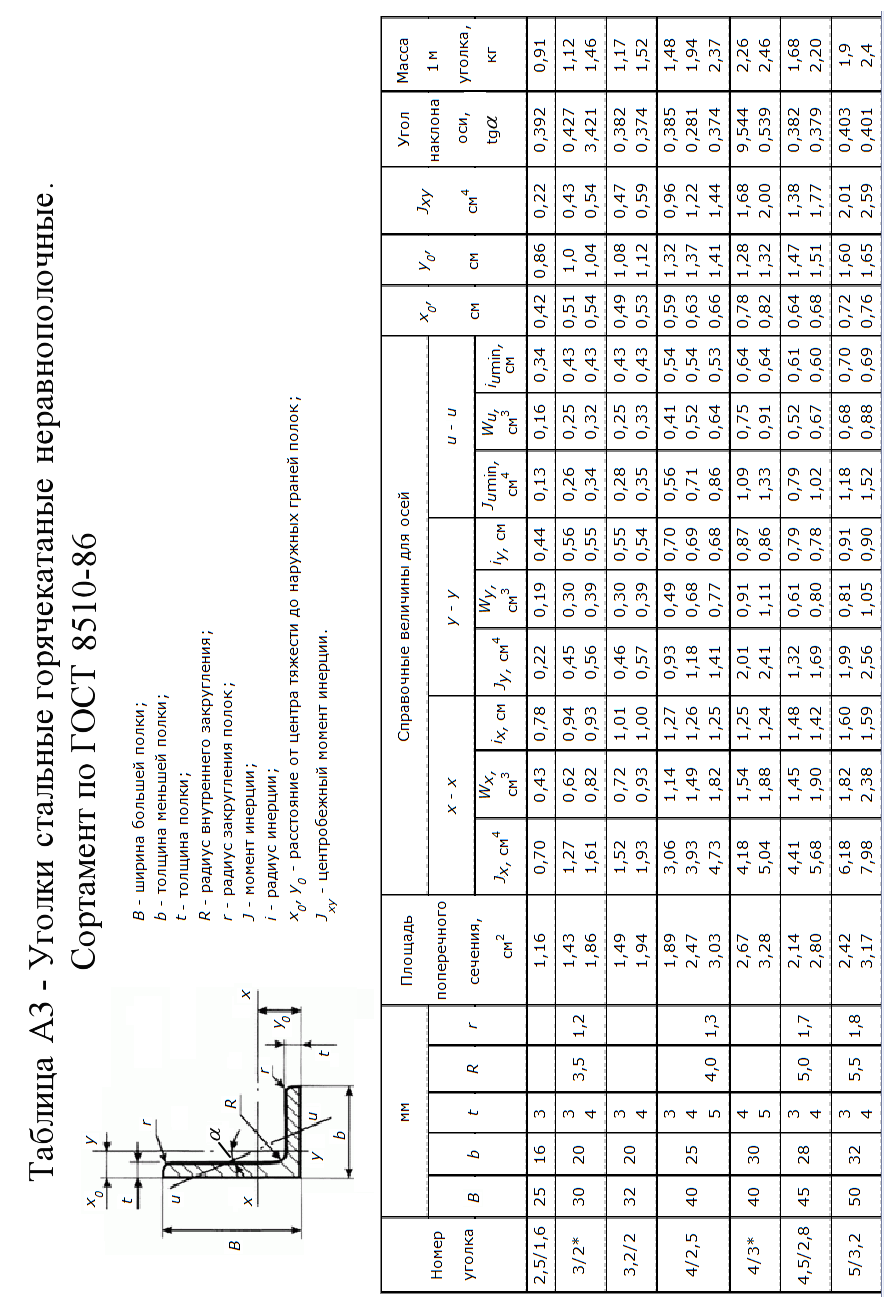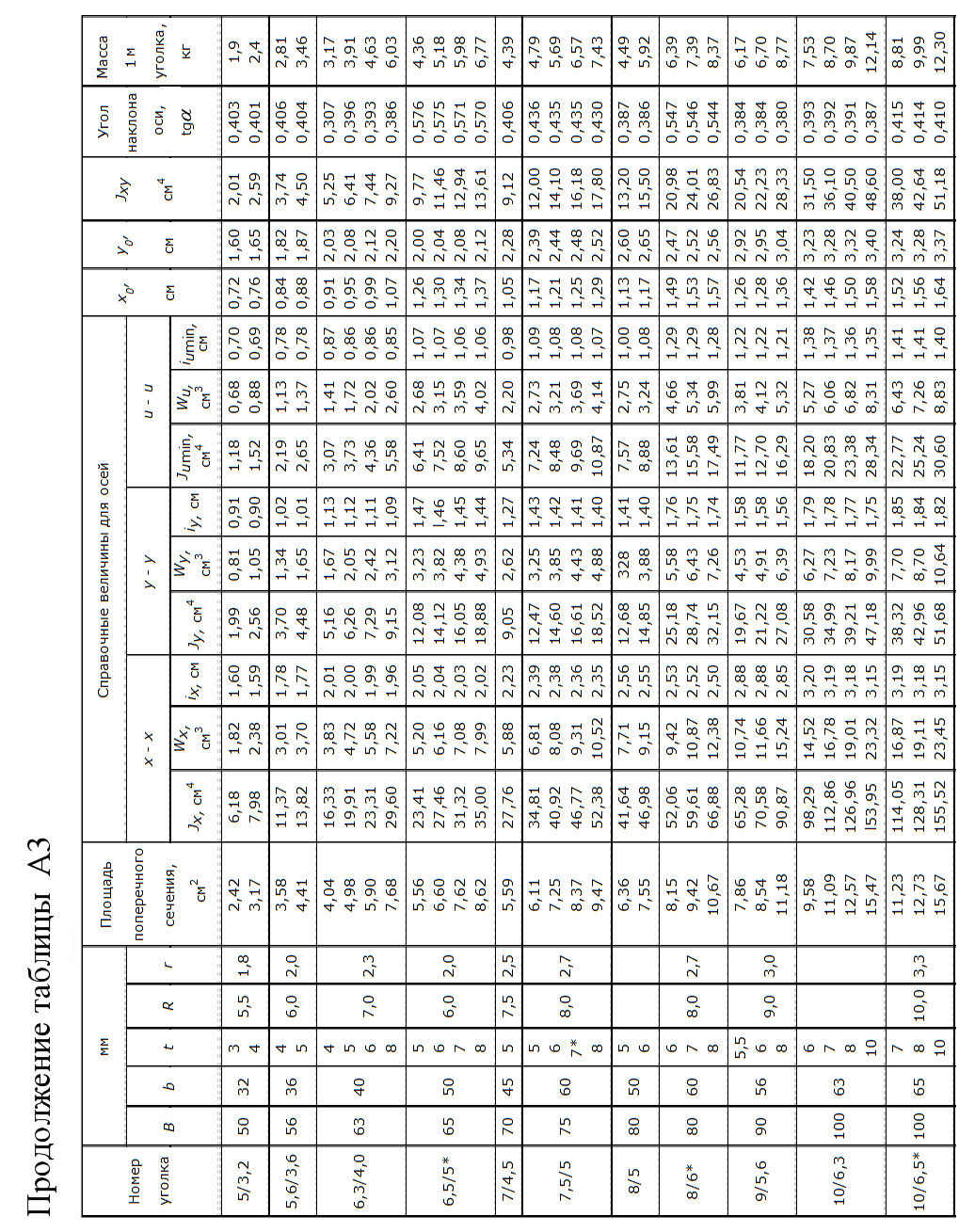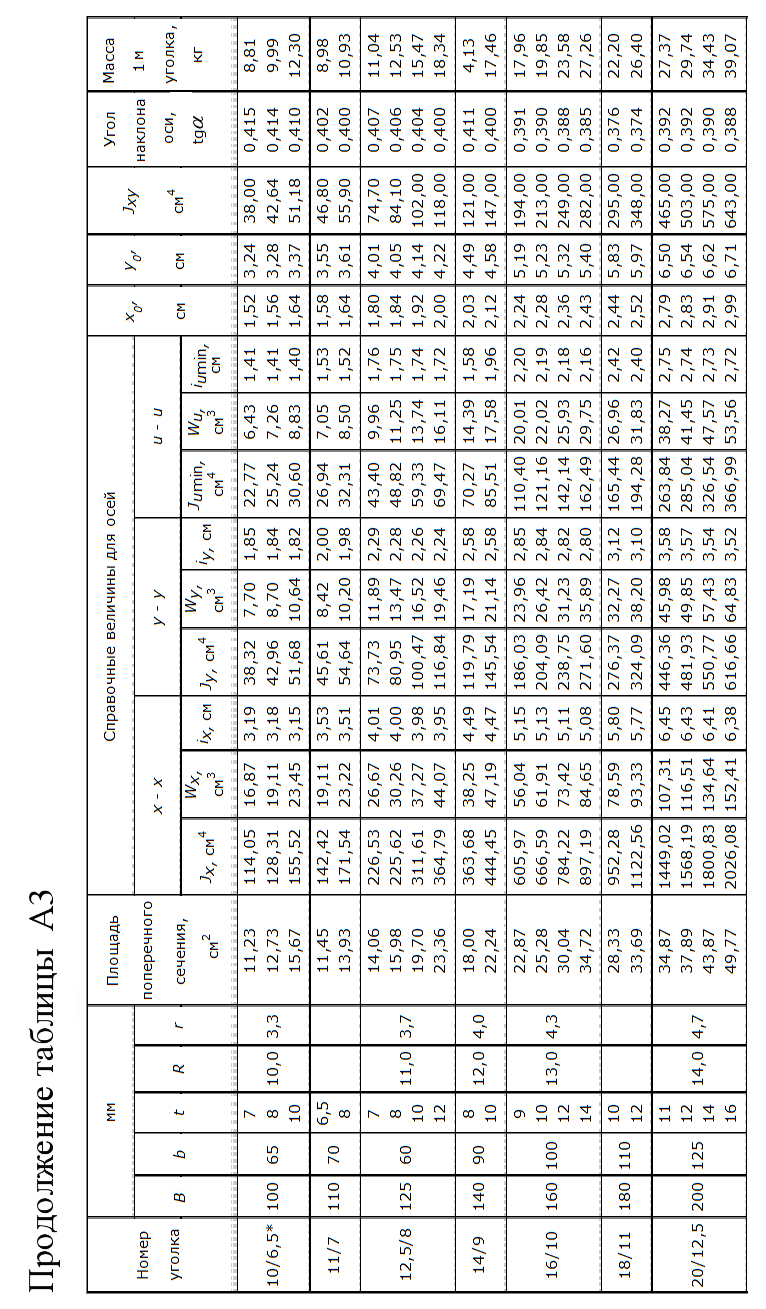
,
,
,
,
,
