Теория вероятности. Задача 1 в группе из 30 учеников на контрольной работе получили оценку отлично

• Название: Задача 1 в группе из 30 учеников на контрольной работе получили оценку отлично
• Дата: 14.02.2022
• Размер: 232.5 Kb.
• Имя файла: Теория вероятности.doc
• Тип: Задача; #361349

Задача 1:

В группе из 30 учеников на контрольной работе получили оценку «отлично» - 6 учеников, «хорошо» - 10 учеников, «удовлетворительно» - 9. Какова вероятность того, что все три ученика, вызванные к доске наугад, имеют по контрольной работе неудовлетворительные оценки.

Решение:

Р(А)=т/п

т – количество благоприятных вариантов

п – количество всевозможных вариантов





Р(А)=10/4060=0,0025=0,25%

Задача 2:

В партии из 100 одинаковых по внешнему виду изделий смешаны 40 штук 1-го сорта и 60 штук 2-го сорта. Найти вероятность того, что взятые наудачу 2 изделия окажутся одного сорта.

Решение:

Р(А)=т/п

т – количество благоприятных вариантов

п – количество всевозможных вариантов





Р(А)=2550/4950=0,515=51,5%

Задача 3:

Из 1000 ламп 100 принадлежит первой партии, 250 – второй, остальные – третьей. В первой партии 6 %, во второй – 5 %, в третьей – 4 % бракованных ламп. Наудачу выбирается одна лампа. Определить вероятность того, что выбранная лампа не бракованная.

Решение:

Н₁ – 1 партия Р(Н₁)=0,1 Р_Н1(А)=1-0,06=0,94

Н₂ – 2 партия Р(Н₂)=0,25 Р_Н2(А)=1-0,05=0,95

Н₃ – 3 партия Р(Н₃)=0,65 Р_Н2(А)=1-0,04=0,96

По формуле полной вероятности:



Задача 4:

Пассажир может обратиться для получения билета в одну из трех касс. Вероятность обращения в каждую кассу зависят от их месторасположения и равны соответственно 0,5;0,2;0,3. Вероятность того, что к моменту прихода пассажира имеющиеся в кассе билеты будут распроданы, для каждой кассы соответственно равны 0,8;0,6;0,7. Пассажир отправился за билетом в одну из касс и приобрел билет. Найти вероятность того, что билет приобретен в первой кассе.

Решение:

Н₁ – 1 касса Р(Н₁)=0,5 Р_Н1(А)=1-0,8=0,2

Н₂ – 2 касса Р(Н₂)=0,2 Р_Н2(А)=1-0,6=0,4

Н₃ – 3 касса Р(Н₃)=0,3 Р_Н2(А)=1-0,7=0,3

По формуле Байеса: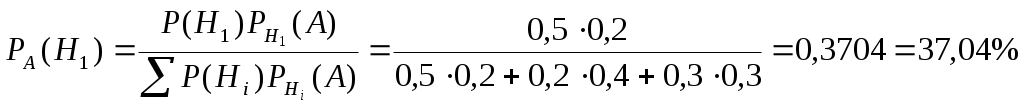



Задача 5:

Вероятность того, что разменный автомат при опускании одной монеты сработает неправильно, равна 0,07. Сколько нужно опустить монет, чтобы наивероятнейшее число случаев правильной работы автомата было равно 100?

Решение:

р=0,07 q=1-р q=1-0,07=0,93

т=100

п= т/q =100/0,93=107,5

п=108 монет

Задача 6:

Вероятность появления события А в одном испытании равна р. Найти вероятность того, что в п независимых испытаниях событие А произойдет: т раз, от k₁ до k₂ раз.

Решение:

1. 
   p=0.16, n=600, m=90
   

q=1-р, q=1-0,16=0,84

По локальной теореме Лапласа

2. 
   n=100, p=0.3, k₁=5, k₂=40
   

q=1-р, q=1-0,3=0,7

По интегральной теореме Лапласа











Задача 7:

Случайная величина μ задана функцией распределения . Требуется найти:

1. 
   постоянную С;
   
2. 
   плотность распределения вероятностей ;
   
3. 
   основные числовые характеристики ;
   
4. 
   вычислить вероятность того, что случайная величина μ примет значение, принадлежащее интервалу (α,β);
   
5. 
   построить графики функций ; .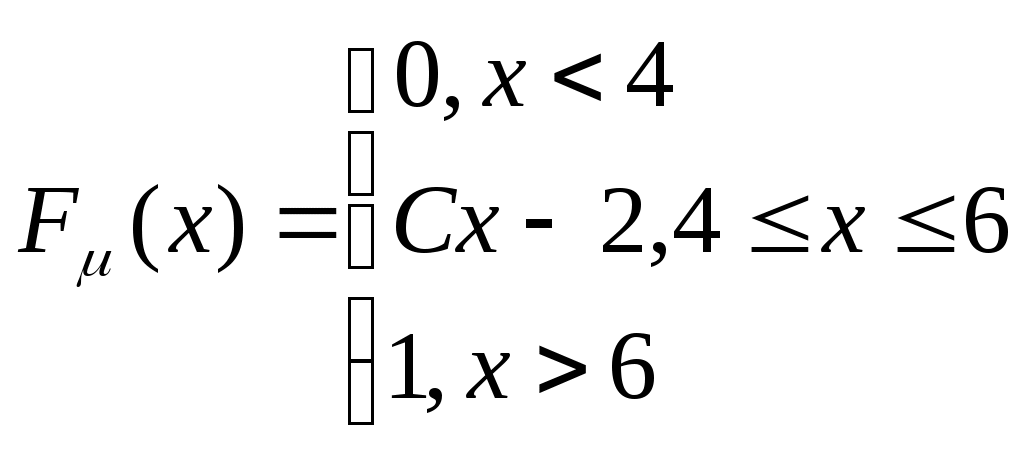
   

Решение: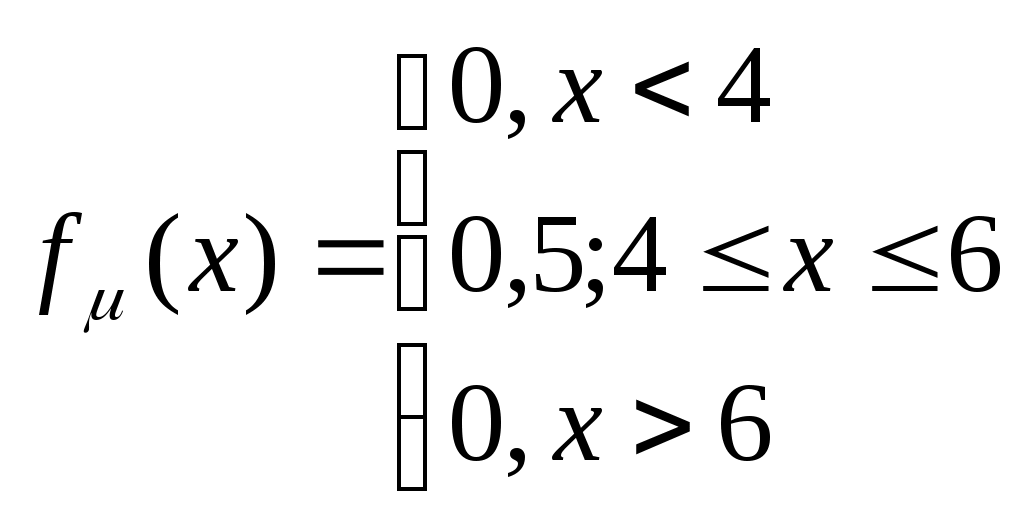

1. 
   С=0.5
   
2. 
   
   

3. 
   
   

4. 
   P(a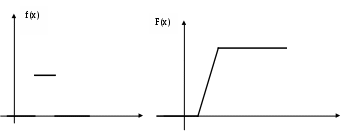

х

х


Задача 8:

Дан закон распределения системы двух случайных величин. Требуется:

1. 
   вычислить коэффициент корреляции и проанализировать тесноту связи между μ и η.
   
2. 
   составить условный закон распределения случайной величины μ и найти условное математическое ожидание.
   
3. 
   составить уравнение прямой регрессии μ на η и построить график.
   

Решение:

μ η	-1	0	1	рη
1	0.2	0.1	0.05	0.35
2	0.1	0.2	0.02	0.32
3	0.08	0.1	0.15	0.33
рμ	0.38	0.4	0.22	1

Находим основные числовые характеристики:

М(μ)=1*0,35+2*0,32+3*0,33=1.98; М(η)=-1*0,38+0*0,4+1*0,22=-0.16;

М(μ²)=1²*0,35+2²*0,32+3²*0,33=4.6; М(η²)=(-1)²*0,38+0²*0,4+1²*0,22=0.6;

D(μ)=4.6-1.98²=0.6796; D(η)=0,6-0,16²=0.5744;

σ(μ)=0,6796^1/2=0.824; σ(η)=0,59^1/2=0,758;

М(μη)=-1*1*0.2+1*1*0.05-1*2*0.1+1*2*0.02-1*3*0.38+1*3*0.15= -1



Находим коэффициент корреляции:

величина коэффициента корреляции говорит о том, что связь между случайными величинами очень тесная.

Условный закон распределения:

μ η	-1	0	1	рη
1	0.53	0.25	0.23	0.35
2	0.26	0.5	0.09	0.32
3	0.21	0.25	0.68	0.33
рμ	0.38	0.4	0.22	1

Находим условные математические ожидания:

М(μ/η=-1)=1*0.53+2*0.26+3*0.21=1.68; М(μ/η=0)=1*0.25+2*0.5+3*0.25=2;

М(μ/η=1)=1*0.23+2*0.09+3*0.22=1.07;

Запишем уравнение линейной регрессии: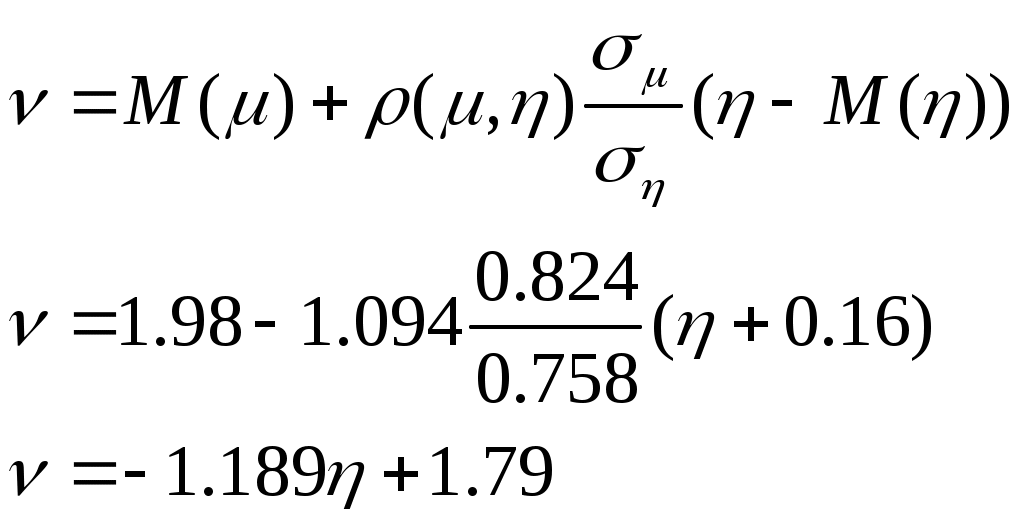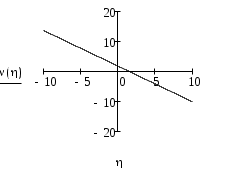





Задача 9:

По данным пчеловодческого хозяйства от 25 наудачу взятых пчелиных семей было получено мёда (в кг):

75 210 350 350 400 520 540 560 590 680 700 700 720

750 780 790 810 850 875 890 1000 1000 1100 1200 1250

α=0,05, γ=0,95, σ=280, h=250, x₀=50

Решение:

Интервальное статистическое распределение:

х	[50,300)	[300,550)	[550,800)	[800,1050)	[1050,1300)
пк	2	5	9	6	3

Теперь посчитаем выборочную среднюю:



Построим полигон и гистограмму частот: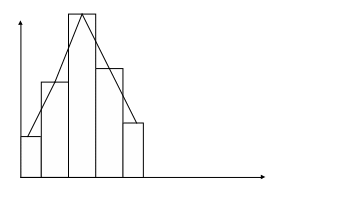

Границы интервалов
50	-2.34	-0.4904
			0.0639
300	-1.45	-0.4265
			0.2177
550	0.55	-0.2088
			0.3419
800	0.34	0.1331
			0.2576
1050	1.23	0.3907
			0.0931
1300	2.13	0.4838

Границы интервалов	Эмпирические частоты	Вероятности	Теоретические частоты	Отклонения
[50,300)	2	0.0639	1.5975	0.4025	0.101
[300,550)	5	0.2177	5.4425	-0.4425	0.036
[550,800)	9	0.3419	8.5475	0.4525	0.024
[800,1050)	6	0.2576	6.44	-0.44	0.030
[1050,1300)	3	0.0931	2.3275	0.6725	0.194

Х²_набл=0.385 Х²_кр=7,82

Х²_набл< Х²_кр – то нет оснований отвергнуть выдвинутую гипотезу, т.е. количественный признак генеральной совокупности имеет нормальное распределение.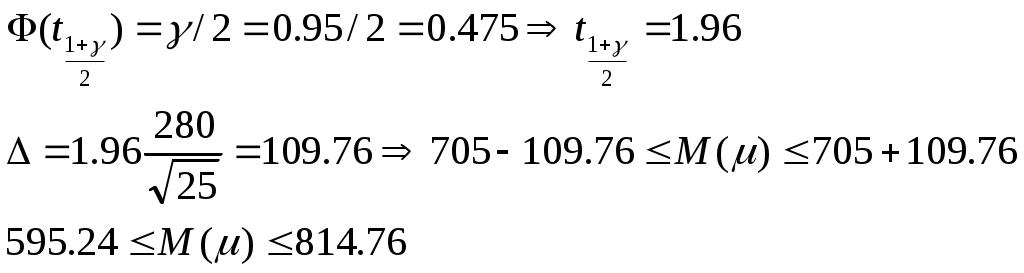





Задача 10:

Данные о живом весе (кг) и молочной продуктивности (кг) 80 коров приведены в таблице:

Решение:

х	у					пх
	325-375	375-425	425-475	475-525	525-575
1250-1750	3					3
1750-2250	2	8	2			12
2250-2750		7	5	13		25
2750-3250		1	10	10	7	28
3250-3750				7	5	12
пу	5	16	17	30	12	80

; ; ; ;

Переходим к условным вариантам: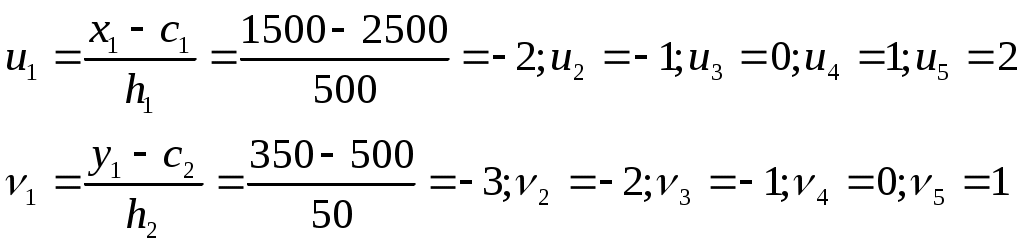

u	ν					пх
	-3	-2	-1	0	1
-2	3					3
-1	2	8	2			12
0		7	5	13		25
1		1	10	10	7	28
2				7	5	12
пу	5	16	17	30	12	80

Вычисляем выборочные характеристики и коэффициент корреляции:



Связь между рассматриваемыми величинами тесная.

Регрессия: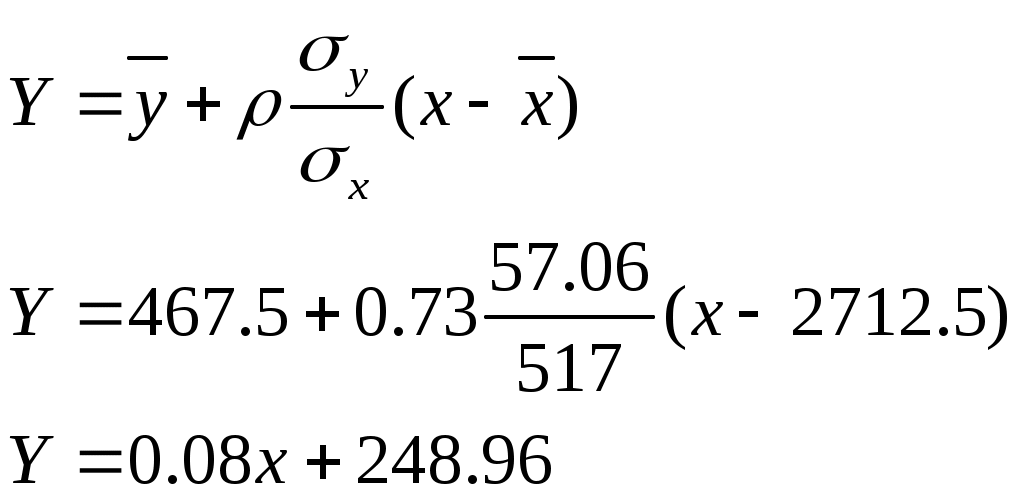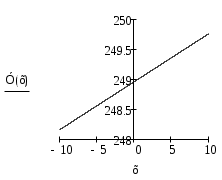