Кр по механики жидкости и газа. Задача 1 в процессе изменения состояния 1 кг газа его внутренняя энергия увеличивается на u
 Скачать 274.46 Kb. Скачать 274.46 Kb.
|
|
Контрольная работа Задача 1 В процессе изменения состояния 1 кг газа его внутренняя энергия увеличивается на Δu. При этом над газом совершается работа, равная l. Начальная температура газа t1, конечное давление Р2. Определить для заданного газа показатель политропы n, начальные и конечные параметры, изменение энтропии ΔS и изменение энтальпии Δh. Представить процесс в P-V и Т-S диаграммах. Изобразить также (без расчета) изобарный, изохорный, изотермический и адиабатный процессы, проходящие через ту же начальную точку. Дайте сравнительный анализ этих процессов. Контрольный вопрос. Какова общая формулировка и математическое выражение Первого закона термодинамики?
Температуру Т2 определим по известному изменению внутренней энергии Δu: 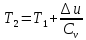 где теплоемкость принимается постоянной величиной, не зависящей от температуры 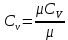 Молярная теплоемкость двухатомного идеального газа (из приложения 1 Методических указаний): 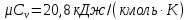 Средняя молярная масса окиси углерода CO (угарный газ) 28,01 кг/кмоль. 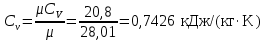 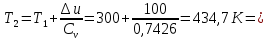 Газовая постоянная окиси углерода CO 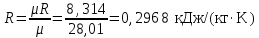 где 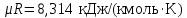 – универсальная газовая постоянная. – универсальная газовая постоянная. Значение показателя политропы 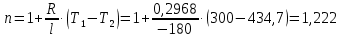 Удельный объем найдем из уравнения состояния газа 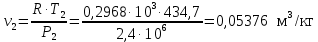 Удельный объем газа в начальном состоянии 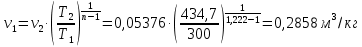 Определим давление в начальном состоянии из уравнения состояния газа 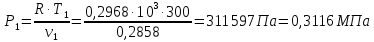 Изменение энтропии в процессе определяется формулой 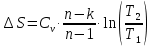 в которой необходимо определить показатель адиабаты 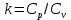 . . Изобарная теплоемкость газа рассчитывается по известной молярной теплоемкости для двухатомного идеального газа 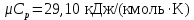 (приложение 1) (приложение 1)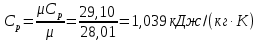 Тогда 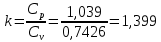 Изменение энтропии 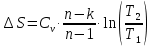 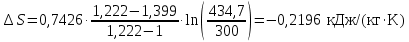 Изменение энтальпии в процессе 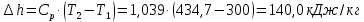 Результаты расчета приведены в таблице и на диаграммах в PV- и ТS-координатах. Таблица 1
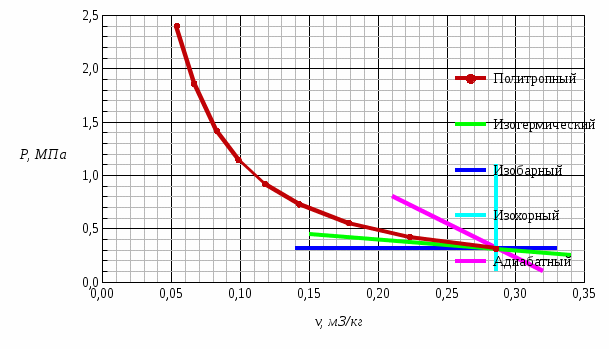 Рис. 1 – Диаграмма изменения состояния окиси углерода CO в PV-координатах 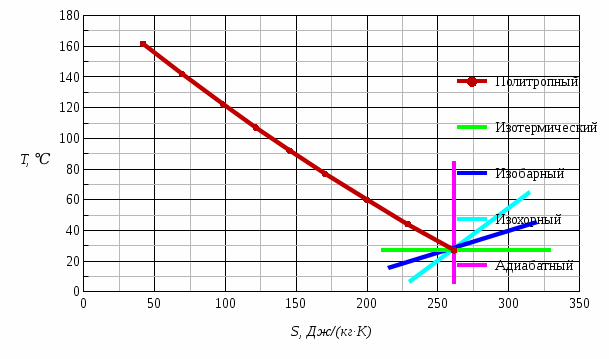 Рис. 2 – Диаграмма изменения состояния окиси углерода CO в ТS-координатах На этих диаграммах изображены также без расчета другие процессы, проходящие через начальную точку: изотермический, изобарный, изохорный и адиабатный. Изменения параметров газа в термодинамических процессах определяются уравнением состояния идеального газа и законом сохранения энергии. Сравнительный анализ процессов Изохорный процесс v = const - давление пропорционально температуре; - внешняя работа равна нулю; - теплота расходуется на изменение внутренней энергии. Изобарный процесс p = const - удельный объем пропорционален температуре; - Первый закон термодинамики имеет вид dq = du + pdv = dh – количество подведенной теплоты равно изменению энтальпии. Изотермический процесс T = const - удельный объем обратно пропорционален давлению; - внутренняя энергия постоянна, соответственно, q = l. Адиабатный процесс q = 0 – протекает без подвода и отвода тепла, соответственно, du= -l. Контрольный вопрос. Какова общая формулировка и математическое выражение Первого закона термодинамики? Первый закон термодинамики является частным случаем всеобщего закона сохранения и превращения энергии применительно к тепловым/термодинамическим явлениям. Общая формулировка В изолированной системе сумма всех видов энергии постоянна. Математическое выражение U = const dU = 0 где U – сумма всех видов энергии. В неизолированной системе, которая может совершать работу и обмениваться теплотой с окружающей средой: теплота, поглощенная системой, расходуется на изменение внутренней энергии системы и на совершение работы против внешних сил Q = ∆U + A Задача 2 Рассчитать параметры рабочего тела в характерных точках идеального цикла поршневого двигателя внутреннего сгорания с изохорно-изобарным подводом теплоты, если известны давление Р1и температура t1 рабочего тела в начале сжатия. Степень сжатия ε, степень повышения давления λ, степень предварительного расширения ρ заданы. Определить работу, получаемую от цикла, его термический КПД и изменение энтропии отдельных процессов цикла. За рабочее тело принять воздух, считая его теплоемкость в расчетном интервале температур постоянной. Построить в масштабе диаграмму этого цикла в P-V и T-S координатах. Контрольный вопрос. В чем смысл Второго закона термодинамики?
Параметры в характерных пяти точках цикла Точка 1 Газовая постоянная воздуха: 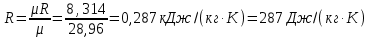 где 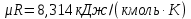 – универсальная газовая постоянная; – универсальная газовая постоянная; μ = 28,96 кг/кмоль – средняя молярная масса воздуха. Удельный объем воздуха 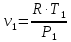 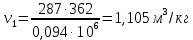 где T1 = 89℃ = 362 К. Точка 2 Процесс 1-2 – адиабатное сжатие. Параметры в точке 2: 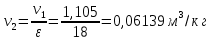 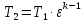 где показатель адиабаты 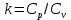 Изобарная теплоемкость воздуха рассчитывается по известной молярной теплоемкости для двухатомного идеального газа 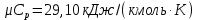 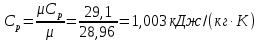 Изохорную теплоемкость воздуха определим как для двухатомного идеального газа по известной величине молярной теплоемкости 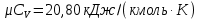 и средней молярной массе воздуха 28,96 кг/кмоль и средней молярной массе воздуха 28,96 кг/кмоль 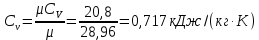 Тогда показатель адиабаты воздуха 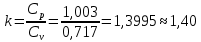 Температура в точке 2 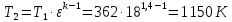 Давление в точке 2 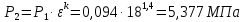 Точка 3 Процесс 2-3 –изохорный процесс подвода теплоты 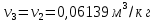 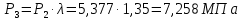 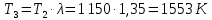 Точка 4 Процесс 3-4 – изобарный процесс подвода теплоты 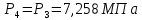 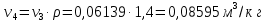 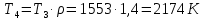 Точка 5 Процесс 5-1 – изохорный 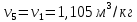 Процесс 4-5 – адиабатное расширение рабочего тела 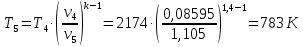 Процесс 5-1 – изохорный 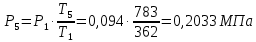 Количество подведенной теплоты 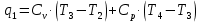 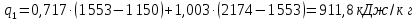 Количество отведенной теплоты 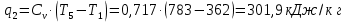 Термический КПД цикла 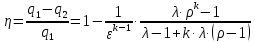 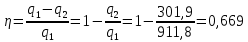 Проверка 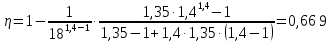 Работа за цикл 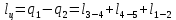 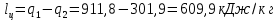 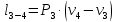 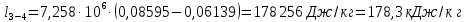 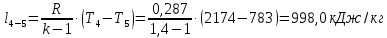 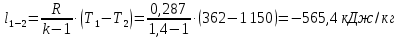 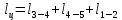 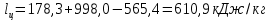 Изменение энтропии 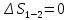 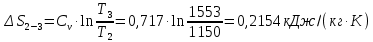 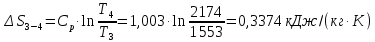 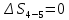 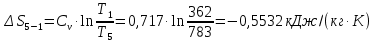 Проверка 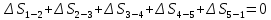  Построение цикла в P-V и T-Sкоординатах Значение энтропии в точке 1 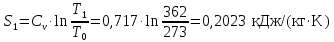 где T0 = 0℃ = 273 К – температура, при которой значение энтропии принято равным нулю (точка начала отсчета энтропии). Контрольный вопрос. В чем смысл Второго закона термодинамики? Физический смысл второго закона термодинамики заключается в том, что любой самопроизвольный процесс протекает в направлении, при котором теплота переходит от горячего тела к холодному. Самопроизвольный переход теплоты от холодного тела к горячему невозможен. Содержание второго закона выражает одностороннюю направленность протекающих в изолированной системе процессов. В связи с чем, вводится понятие энтропии, как функции состояния термодинамической системы, и понятие абсолютного нуля температуры. 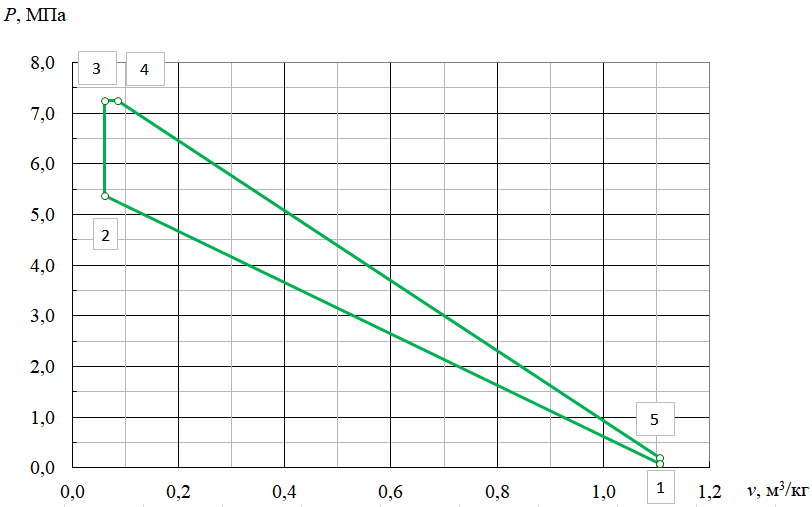 Рис. 3 – Цикл поршневого двигателя внутреннего сгорания с изохорно-изобарным подводом теплоты в P-V–координатах 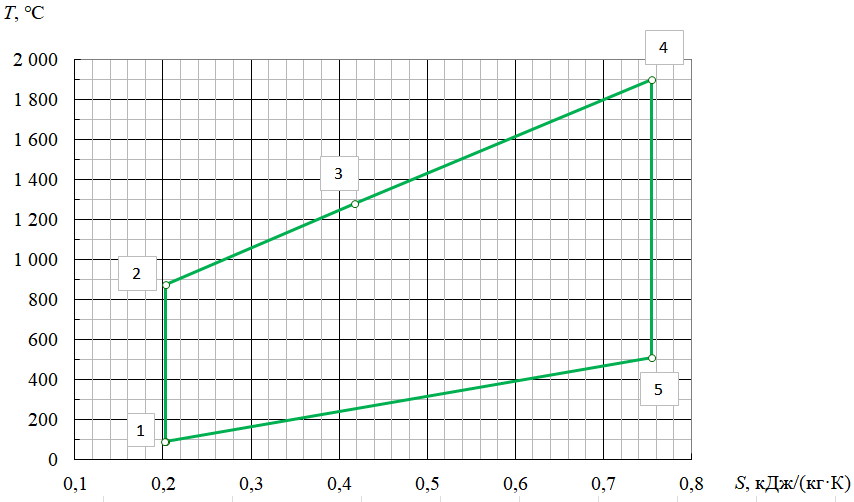 Рис. 4 – Цикл поршневого двигателя внутреннего сгорания с изохорно-изобарным подводом теплоты в T-S–координатах Задача 3 Компрессор всасывает V, м3/ч, воздуха при давлении Р1, МПа и температуре t1,°С. Конечное давление составляет Р2. Найти теоретическую мощность двигателя привода компрессора и расход охлаждающей воды, если температура ее повышается на Δt. Расчет произвести для изотермического, адиабатного и политропного сжатия. Показатель политропы принять равным n, показатель адиабаты равным k, а теплоемкость воды принять равной 4,19 кДж/(кг·К). Покажите в P-V и T-Sкоординатах действительную индикаторную и теоретическую диаграммы. Контрольный вопрос. Какой процесс сжатия в компрессоре является самым эффективным? Чем отличается действительная индикаторная диаграмма от теоретической?
1. Изотермическое сжатие Работа сжатия 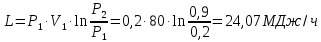 Теоретическая мощность двигателя 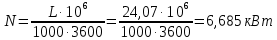 Теплота, отводимая с охлаждающей водой 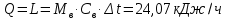 откуда расход охлаждающей воды 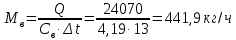 2. Адиабатное сжатие, работа сжатия 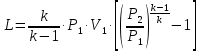 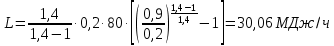 Теоретическая мощность двигателя 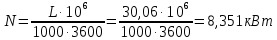 3. Политропное сжатие 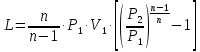 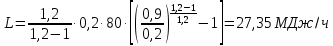 Теоретическая мощность двигателя 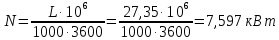 Количество теплоты, которое необходимо отвести от рабочего тела охлаждением 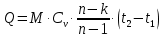 где расход воздуха 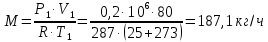 Температура воздуха в конце сжатия 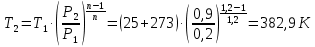 Тогда количество тепла, которое необходимо отвести от рабочего тела охлаждением 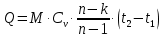 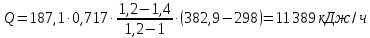 Расход охлаждающей воды 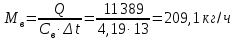 4. Покажите в P-V и T-Sкоординатах действительную индикаторную и теоретическую диаграммы. Процесс сжатия газа в компрессоре в зависимости от условий теплообмена между рабочим телом и стенками цилиндра может осуществляться: - по адиабате 1-2(n=k), - по изотерме 1-2(n=1), - по политропе 1-2 (nk), - по политропе 1-2(nk). Теоретическая диаграмма получения сжатого газа в компрессоре в зависимости от способа сжатия 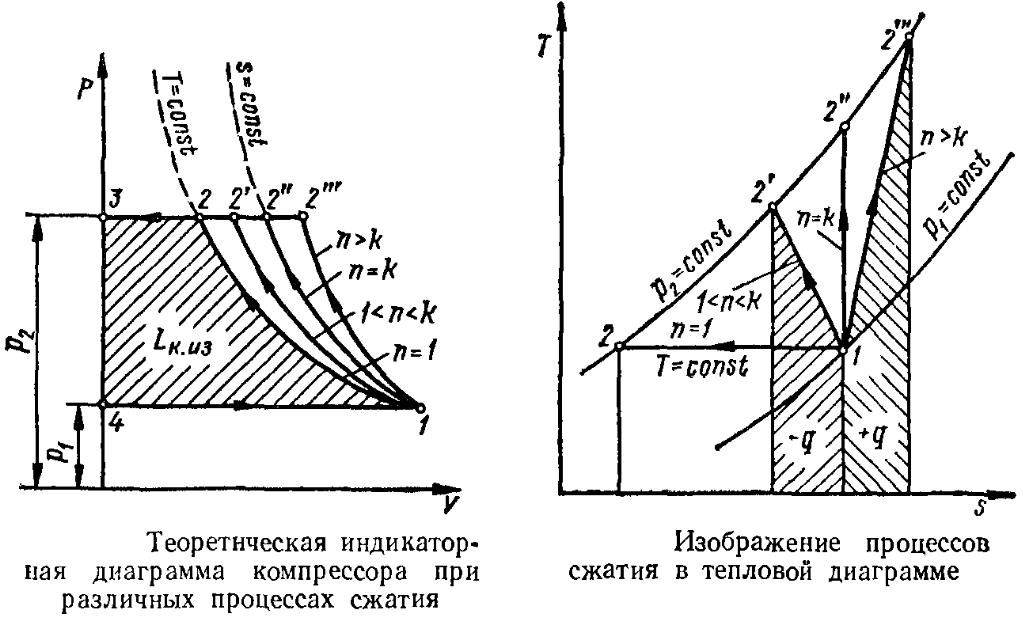 Действительная индикаторная диаграмма компрессора 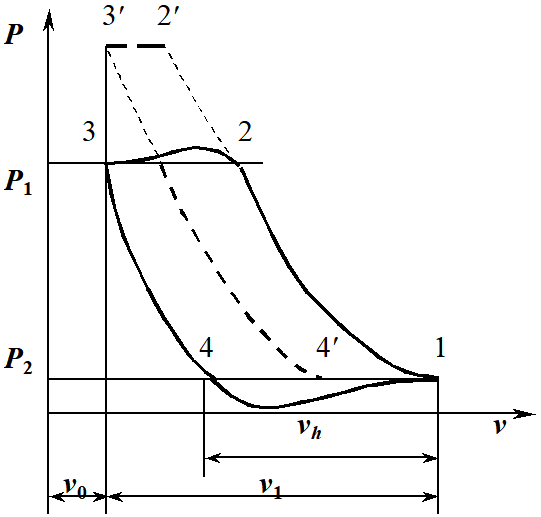 Контрольный вопрос. Какой процесс сжатия в компрессоре является самым эффективным? Чем отличается действительная индикаторная диаграмма от теоретической? Наиболее выгодным с точки зрения затраты работы является изотермический процесс сжатия. Это видно из индикаторной диаграммы в P-V координатах, где работа компрессора отображается площадями фигур: - для изотермического процесса сжатия – площадь 1234; - для политропного процесса сжатия – площадь 12ˊ34 и 12ˊˊˊ34; - для адиабатного процесса сжатия – площадь 12ˊˊ34. Действительная индикаторная диаграмма компрессора отличается от теоретической. Это отличие обусловлено: - потерями на дросселирование во впускном и нагнетательном клапанах компрессора; - наличием вредного пространства (между поршнем, находящемся в крайнем верхнем положении, и крышкой цилиндра с клапанами всегда должен быть зазор, поэтому не весь газ выталкивается из цилиндра). Задача 4 Компрессор аммиачной холодильной установки всасывает пар аммиака при температуре t1,°С, и степени сухости X1 и сжимает его адиабатно до давления, при котором его температура становится равной t2и степень сухости X2 = 1. В конденсаторе охлаждается пар аммиака, охлаждающая вода имеет на входе температуру t'в,°С, а на выходе t''в. В редукционном вентиле жидкий аммиак дросселируется до давления Рдр, после чего он направляется в испаритель, из которого выходит со степенью сухости X1 и снова поступает в компрессор. Теплота, необходимая для испарения аммиака, берется из рассола, имеющего на входе t'р,°С, а на выходе t''р. Определить теоретическую мощность двигателя холодильной машины и часовой расход аммиака, рассола и охлаждающей воды, если холодопроизводительность установки Q0. Теплоемкость рассола принять равной теплоемкости воды. Контрольный вопрос. Сформулируйте второй закон термодинамики для холодильной машины.
Работа, затраченная на привод компрессора 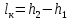 Энтальпия пара аммиака, выходящего из компрессора, поскольку он является сухим насыщенным, определяется по приложению 2 по температуре t2 = 25°С: 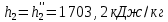 Энтальпия влажного пара аммиака, всасываемого компрессором, определяется по выражению для влажного пара 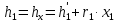 По приложению 2 находим при температуре t1 = -5°С: - энтальпию жидкого аммиака в состоянии насыщения 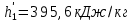 - теплоту фазового перехода аммиака в испарителе 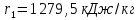 Тогда энтальпия влажного пара аммиака после испарителя на входе в компрессор 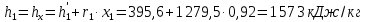 Удельная работа, затраченная на привод компрессора 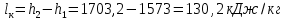 Расход холодильного агента (аммиака), всасываемого компрессором 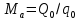 где q0 – удельная холодопроизводительность, определяется как разность энтальпий аммиака в испарителе 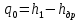 Так как в процессе дросселирования энтальпия аммиака постоянна, то энтальпия после дросселя будет равна энтальпии конденсата после конденсатора при температуре насыщения T2 = 25℃. По приложению 2: 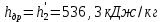 Тогда удельная холодопроизводительность 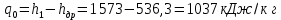 Расход аммиака через компрессор 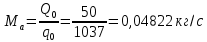 Часовой расход аммиака 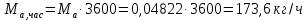 Теоретическая мощность двигателя холодильной машины 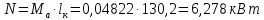 Теплота фазового перехода аммиака в конденсаторе при температуре насыщения T2 = 25℃ (приложение 2) 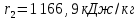 Необходимый расход охлаждающей воды 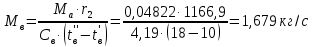 Часовой расход охлаждающей воды 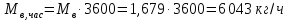 Расход рассола 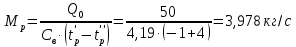 Часовой расход рассола 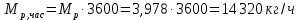 Контрольный вопрос. Сформулируйте второй закон термодинамики для холодильной машины. Машины, отбирающие теплоту от холодного тела и передающие ее более нагретому, называются холодильными. Принцип действия холодильных машин основан на втором законе термодинамики: для передачи теплоты от холодного тела к более горячему необходима затрата внешней работы. Математически второй закон термодинамики выражается уравнением: |Q| = |Q0| + |L| где: |Q| – абсолютное значение теплоты, переданной теплому телу; |Q0| – абсолютное значение теплоты, отведенной от холодного тела; |L| – внешняя работа, затраченная на передачу теплоты. Задача 5 Определить потери теплоты за 1 час с 1 м длины горизонтально расположенной цилиндрической трубы, охлаждаемой свободным потоком воздуха, если известны наружный диаметр d, мм, трубы, температура внешней поверхности трубы tст и температура воздуха в помещении tв. Контрольный вопрос. Какими основными критериями подобия определяется конвективная теплоотдача и каков физический смысл этих критериев?
Потери теплоты от горизонтально расположенной трубы определяем по аналитическому выражению Ньютона-Рихмана для конвективного теплообмена 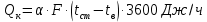 где площадь поверхности трубы длиной 1 м 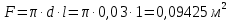 Коэффициент теплоотдачи 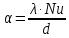 Коэффициент теплопроводности воздуха λ (приложение 3) при определяющей температуре: 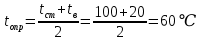 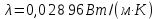 Критерий Нуссельта 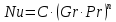 Критерий Грасгофа 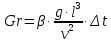 где: 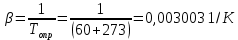 l – определяющий размер, для горизонтальной трубы l=d=0,03 м; ν – кинематическая вязкость воздуха (приложение 3) при определяющей температуре 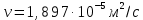 Температурный напор 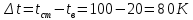 Критерий Грасгофа 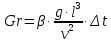 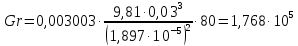 Число Прандтля воздуха (приложение 3) при определяющей температуре t = 60℃ 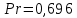 Произведение 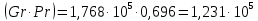 Для данного значения (Gr·Pr) по приложению 4 находим значения эмпирических коэффициентов: 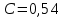 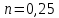 Тогда число Нуссельта 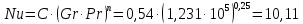 Коэффициент теплоотдачи 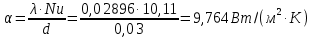 Потери теплоты за 1 час с 1 м длины от горизонтально расположенной трубы 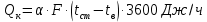 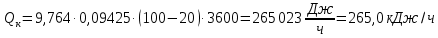 Контрольный вопрос. Какими основными критериями подобия определяется конвективная теплоотдача и каков физический смысл этих критериев? Конвективная теплоотдача определяется следующими основными критериями подобия: Нуссельта, Рейнольдса, Прандтля, Пекле, Грасгофа и Архимеда. Число Нуссельта Nu – «безразмерный коэффициент теплоотдачи». Число Нуссельта (определяемый параметр) выражается в виде эмпирических расчетных формул в зависимости от других (определяющих) безразмерных комплексов (критериев подобия режимов течения и теплообмена): - число Рейнольдса Re – является мерой отношения сил инерции и сил вязкости – определяет режим течения среды (ламинарный или турбулентный); - число Прандтля Pr – характеризует теплофизические свойства среды в отношении вязкости и температуропроводности; - число Пекле Pe – произведение чисел Рейнольдса и Прандтля; - число Грасгофа Gr и число Архимеда Ar – характеризуют подъемную силу, возникающую за счет разности плотностей, по отношению к силам вязкого трения. |
