Задача №14
Случайная величина 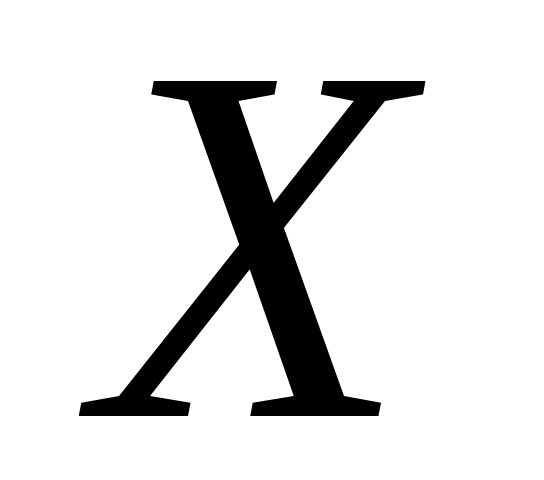 задана функцией распределения задана функцией распределения 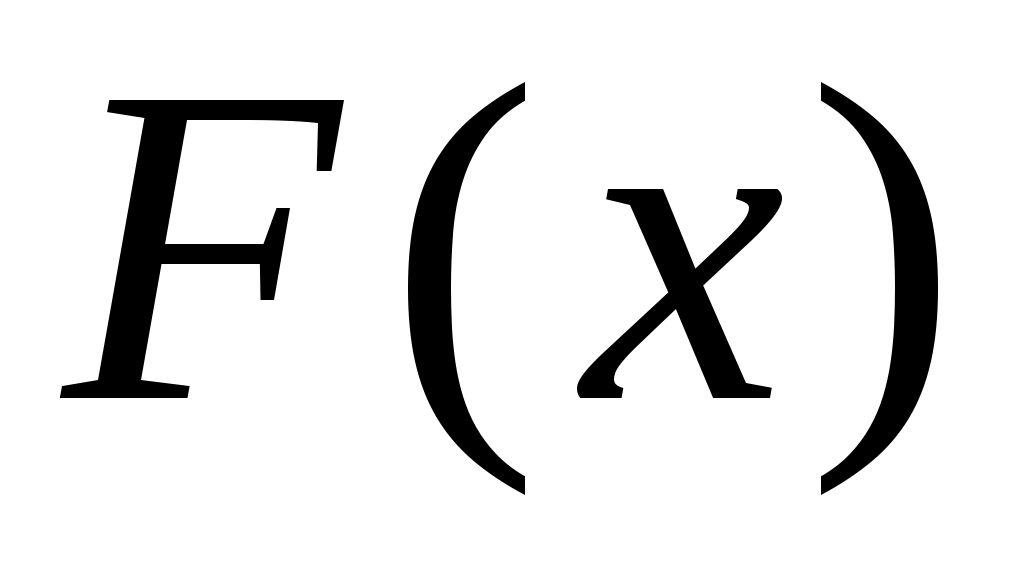 , требуется: , требуется:
1) найти плотность вероятности;
2) математическое ожидание и дисперсию 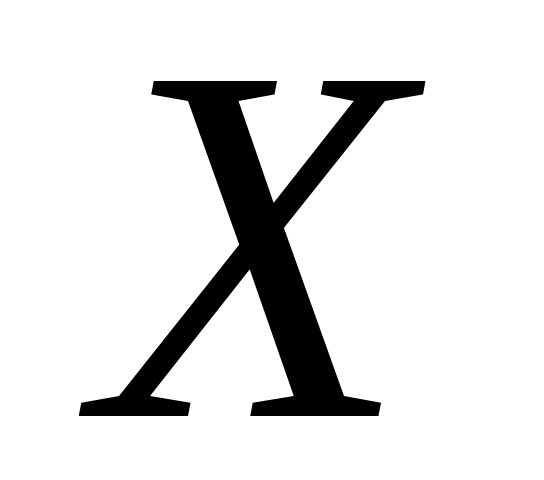 ; ;
3) построить графики функции распределения и функции плотности распределения.
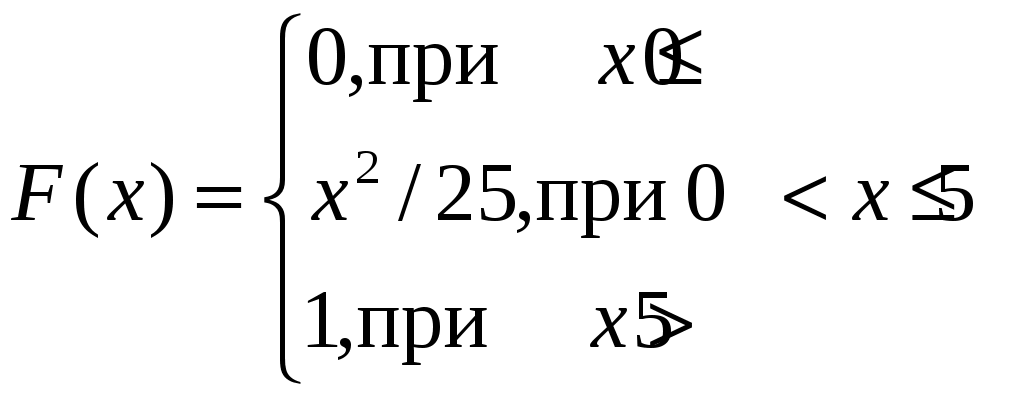 . .
Решение
Найдём плотность распределения. По определению:
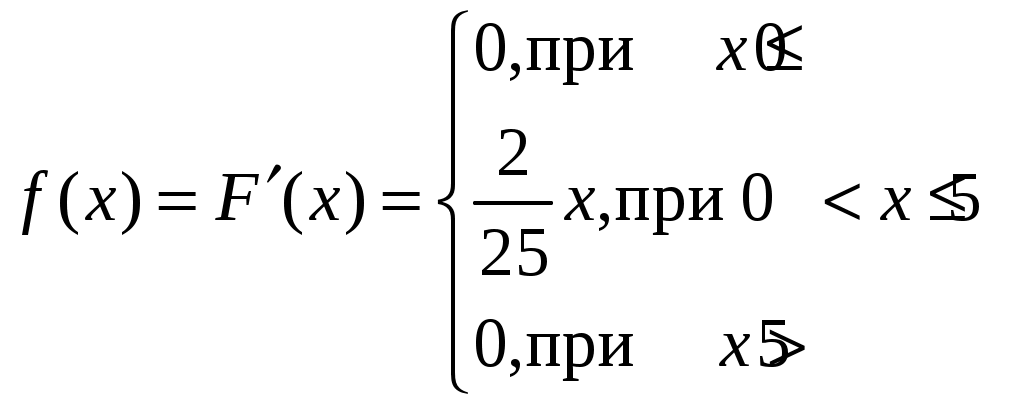 . .
Тогда
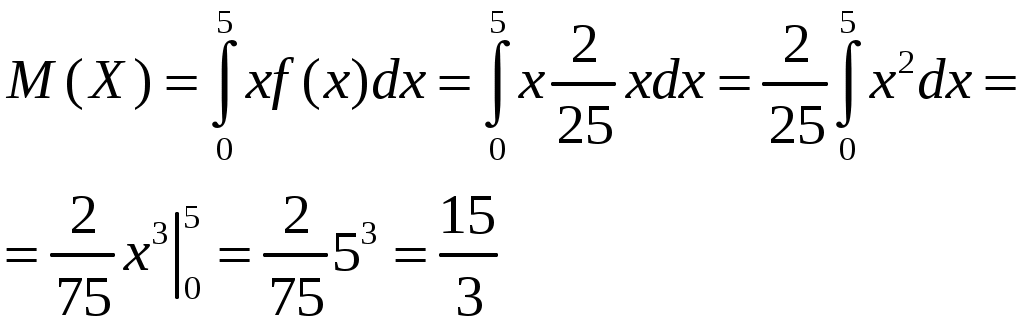 , ,
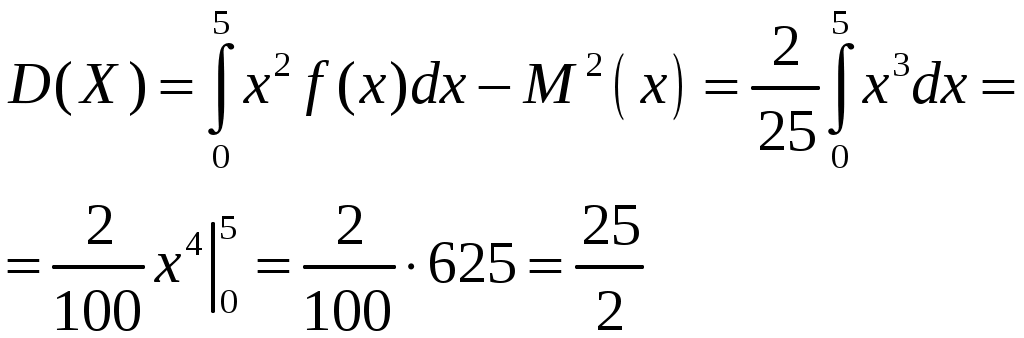 . .
График функции распределения представлен на рисунке а)
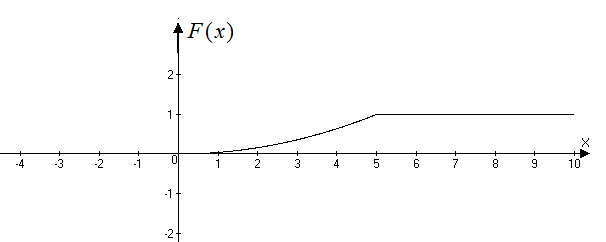
Рисунок а
График функции плотности распределения представлен на рисунке б).
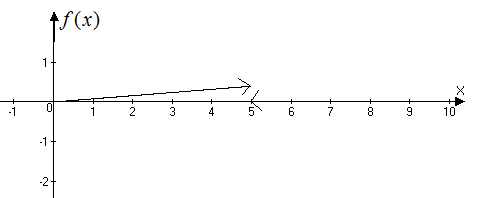
Рисунок б
Задача №15
Заданы математическое ожидание 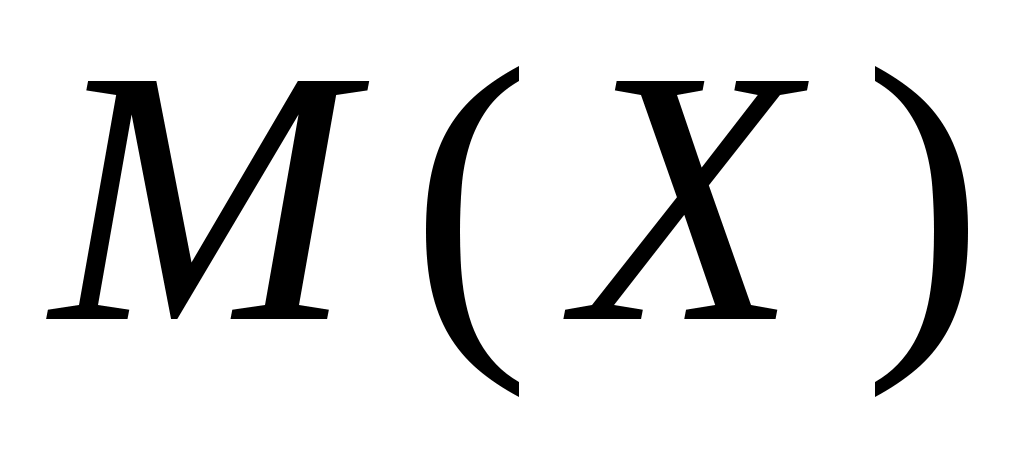 и средне квадратическое отклонение и средне квадратическое отклонение  нормально распределённой величины нормально распределённой величины 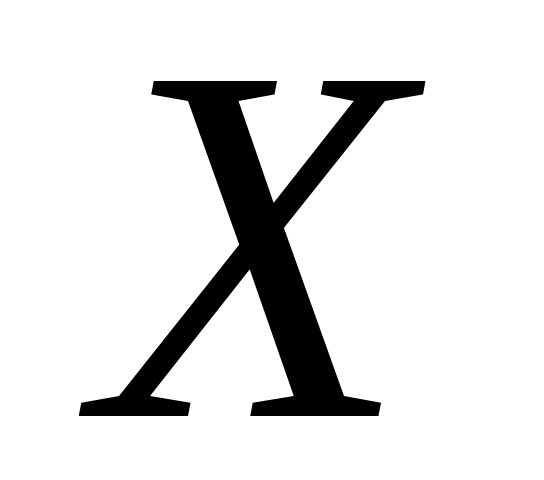 . Найти: 1) вероятность того, что . Найти: 1) вероятность того, что 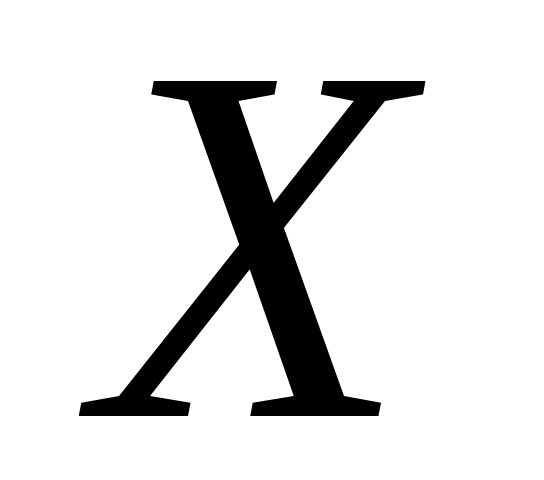 примет значение, принадлежащие интервалу примет значение, принадлежащие интервалу 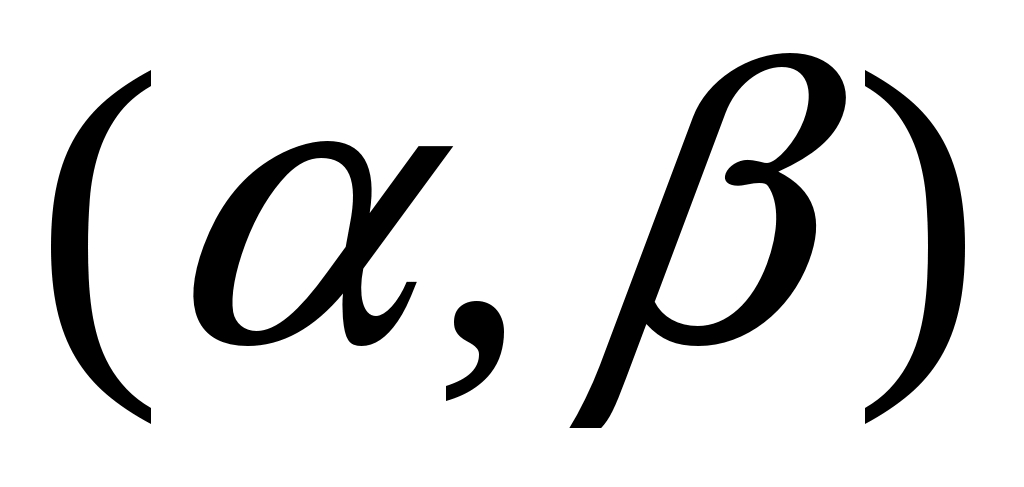 ; 2) вероятность того, что абсолютная величина отклонения ; 2) вероятность того, что абсолютная величина отклонения 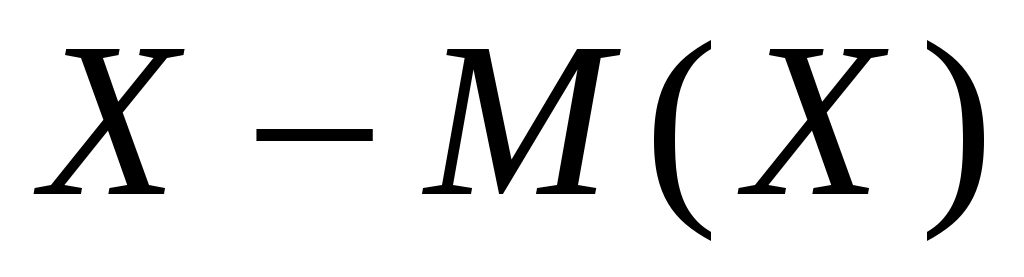 окажется меньше окажется меньше 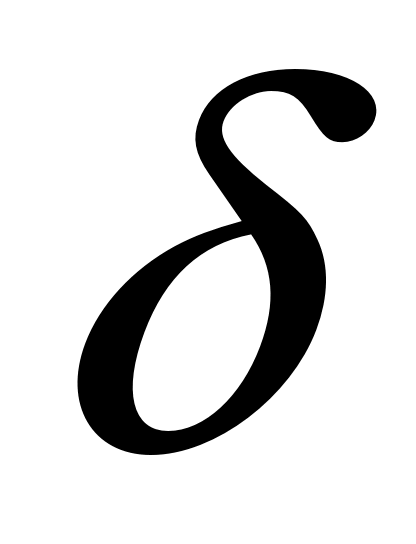 . .
 . .
Решение
1) Воспользуемся формулой:
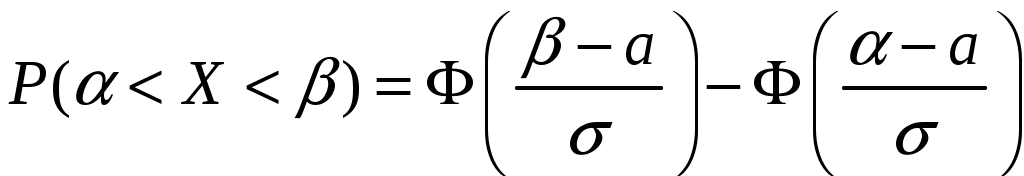 , ,
подставив 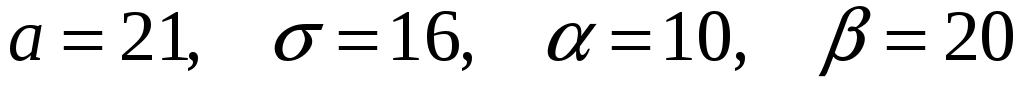 , получим: , получим:
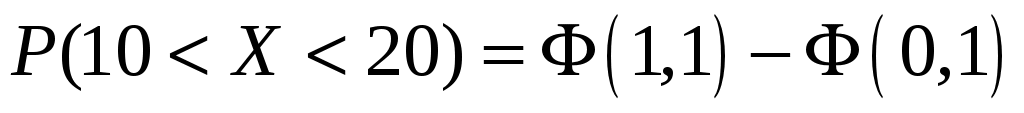 . .
По таблицам приложения находим 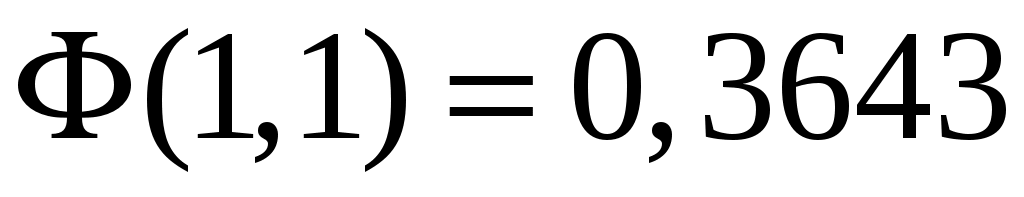 ; ; 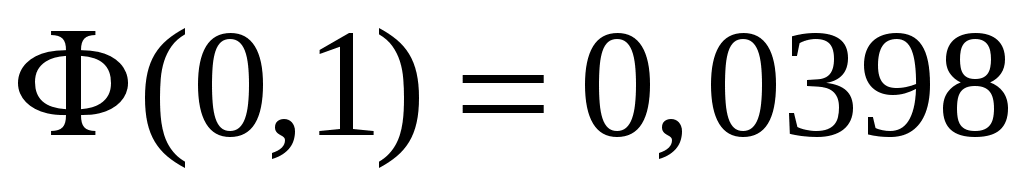 . Тогда искомая вероятность равна: . Тогда искомая вероятность равна:
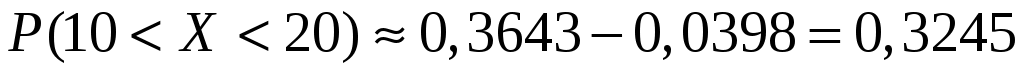 . .
2) Искомая вероятность находится по формуле:
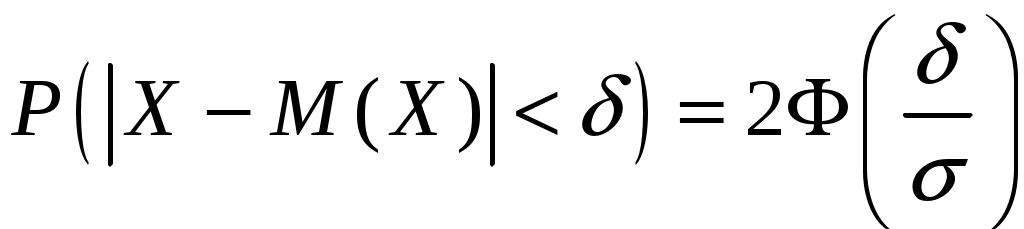 . .
По условию 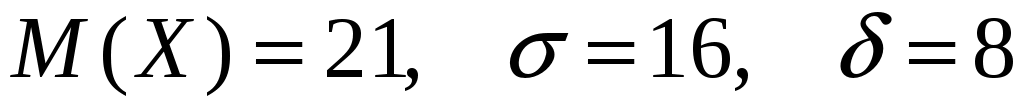 . Следовательно: . Следовательно:
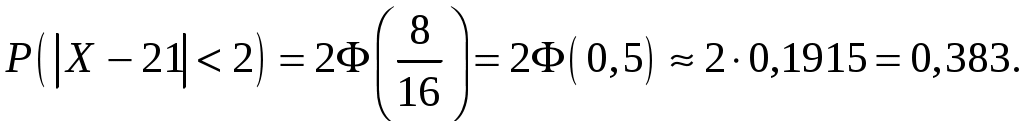
Задача №16
Провести исследование генеральной совокупности, используя выборочные данные соответствующего варианта.
1) Построить статистическое распределение выборки и гистограмму частот (шаг 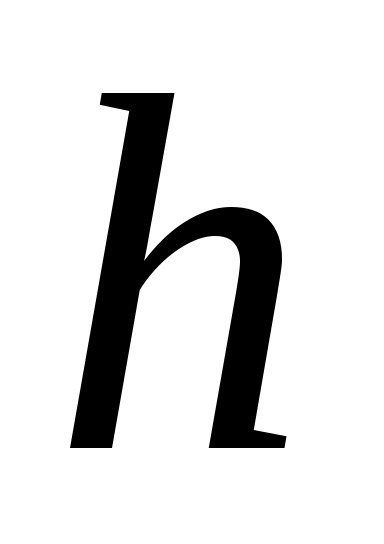 указан в варианте). указан в варианте).
2) Дать точечные оценки генеральному среднему и дисперсии.
3) Предполагая, что выборка сделана из нормальной совокупности, построить доверительные интервалы для математического ожидания и дисперсии нормального распределения, приняв доверительную вероятность 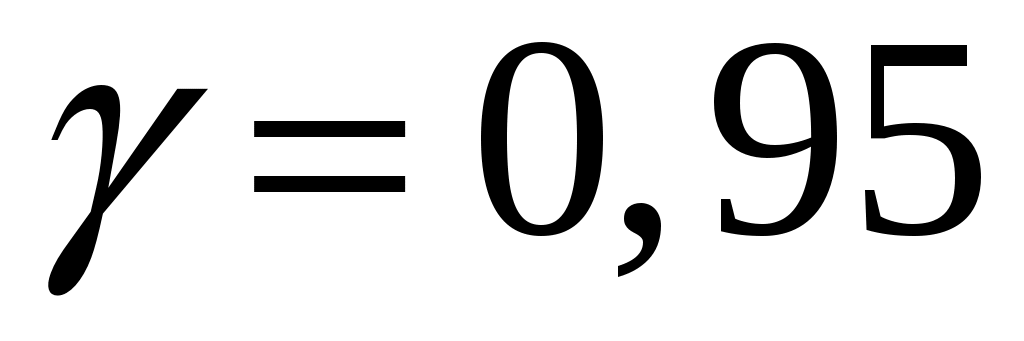 . .
4) При уровне значимости  =0,01 проверить гипотезу о нормальности генеральной совокупности, используя критерий согласия Пирсона [9]. =0,01 проверить гипотезу о нормальности генеральной совокупности, используя критерий согласия Пирсона [9].
Выборка объёма 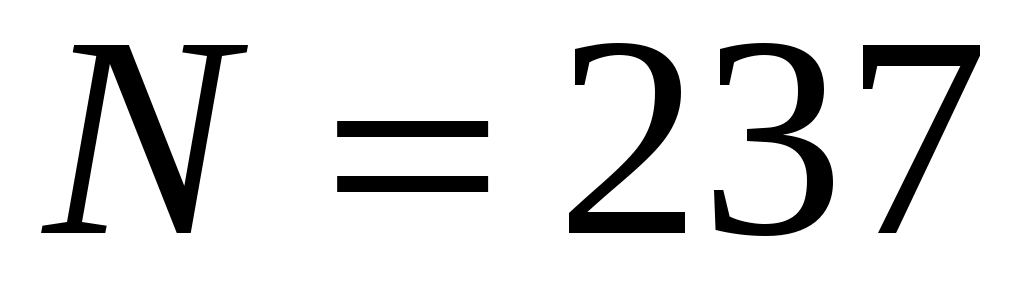 , начало первого интервала , начало первого интервала 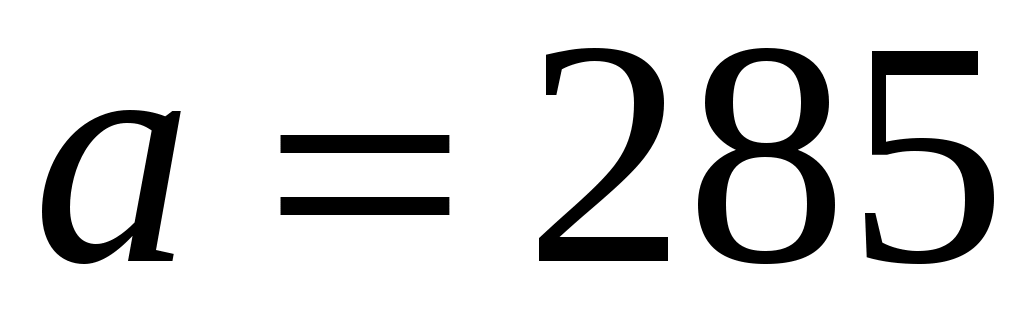 , шаг , шаг 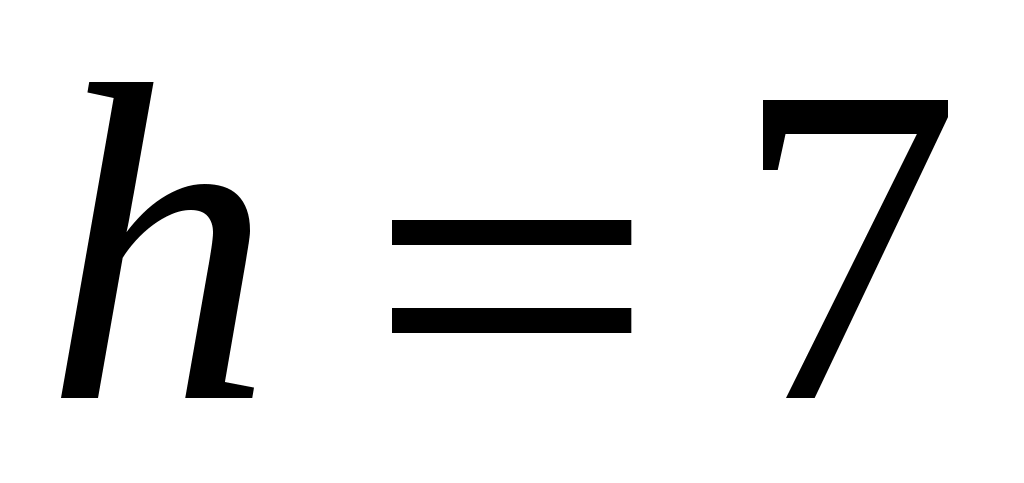 . .
324
|
296
|
313
|
323
|
312
|
321
|
322
|
301
|
337
|
322
|
329
|
307
|
301
|
328
|
312
|
318
|
327
|
315
|
319
|
317
|
309
|
334
|
323
|
340
|
326
|
322
|
314
|
335
|
313
|
322
|
319
|
325
|
312
|
300
|
323
|
335
|
339
|
326
|
298
|
298
|
337
|
322
|
303
|
314
|
315
|
310
|
316
|
321
|
312
|
315
|
331
|
322
|
321
|
336
|
328
|
315
|
338
|
318
|
327
|
323
|
325
|
314
|
297
|
303
|
322
|
314
|
317
|
330
|
318
|
320
|
312
|
333
|
332
|
319
|
325
|
319
|
307
|
305
|
316
|
330
|
318
|
335
|
327
|
321
|
332
|
288
|
322
|
334
|
295
|
318
|
329
|
305
|
310
|
304
|
326
|
319
|
317
|
316
|
316
|
307
|
309
|
309
|
328
|
317
|
317
|
322
|
316
|
304
|
303
|
350
|
309
|
327
|
345
|
329
|
338
|
311
|
316
|
324
|
310
|
306
|
308
|
302
|
315
|
314
|
343
|
320
|
304
|
310
|
345
|
312
|
330
|
324
|
308
|
326
|
313
|
320
|
328
|
309
|
306
|
306
|
308
|
324
|
312
|
309
|
324
|
321
|
313
|
330
|
330
|
315
|
320
|
313
|
302
|
295
|
337
|
346
|
327
|
320
|
307
|
305
|
323
|
331
|
345
|
315
|
318
|
331
|
322
|
315
|
304
|
324
|
317
|
322
|
312
|
314
|
308
|
303
|
333
|
321
|
312
|
323
|
317
|
288
|
317
|
327
|
292
|
316
|
322
|
319
|
313
|
328
|
313
|
309
|
329
|
313
|
334
|
314
|
320
|
301
|
329
|
319
|
332
|
316
|
300
|
300
|
304
|
306
|
314
|
323
|
318
|
337
|
325
|
321
|
322
|
288
|
313
|
314
|
307
|
329
|
302
|
300
|
316
|
321
|
315
|
323
|
331
|
318
|
334
|
316
|
328
|
294
|
288
|
312
|
312
|
315
|
321
|
332
|
319
|
|
|
|
Решение
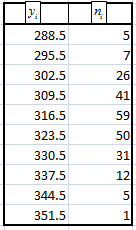
1. Упорядочив данные 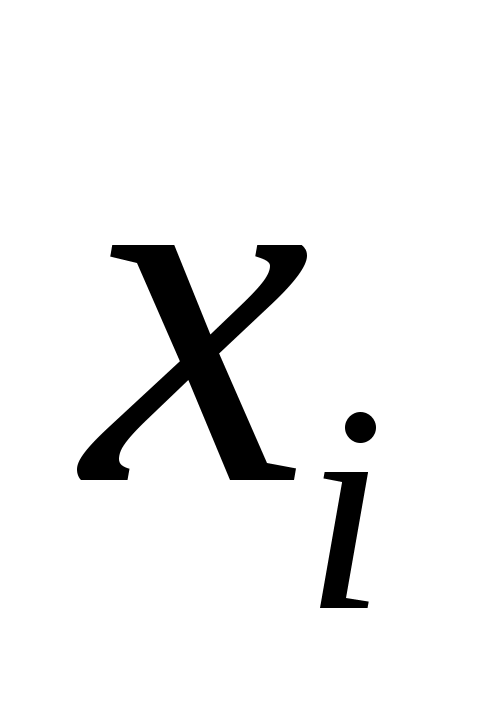 выборки по возрастанию, и найдя соответствующие частоты выборки по возрастанию, и найдя соответствующие частоты 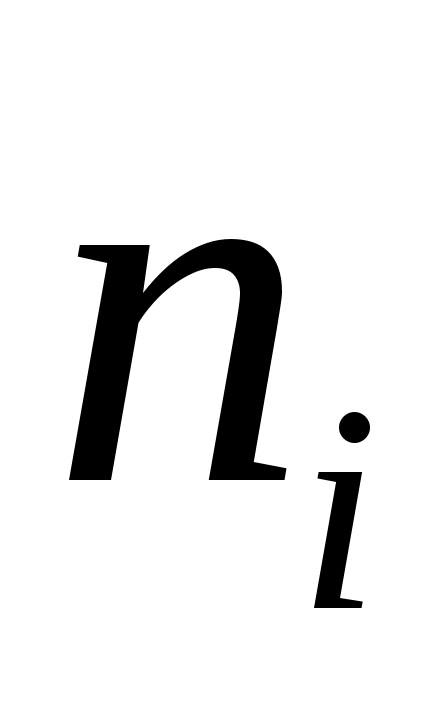 встречающихся значений, получим таблицу, задающую статистическое распределение выборки: встречающихся значений, получим таблицу, задающую статистическое распределение выборки:
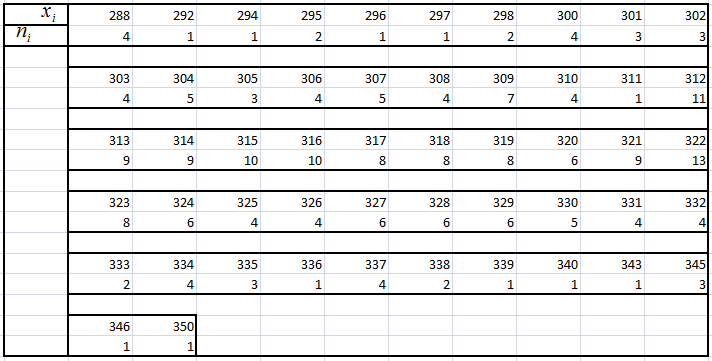
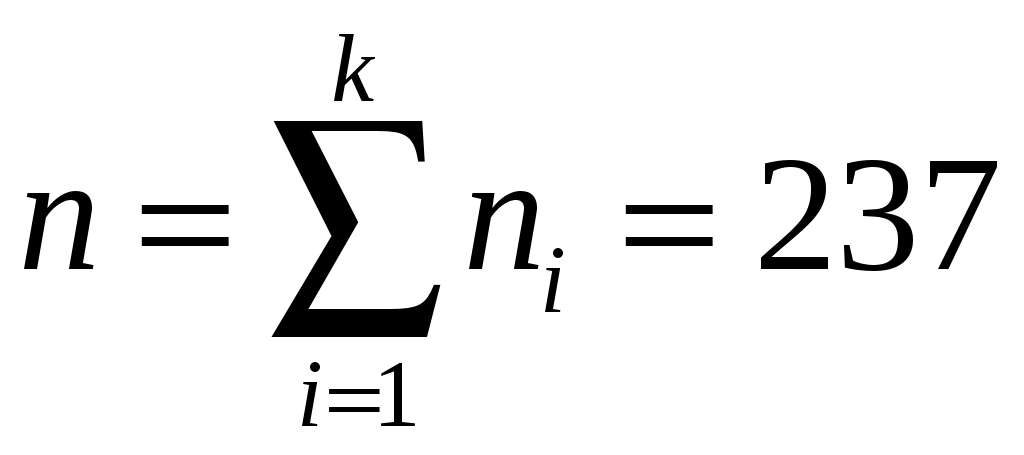 – объём выборки. – объём выборки.
Разобьём интервал данных на 10 частичных интервала длины 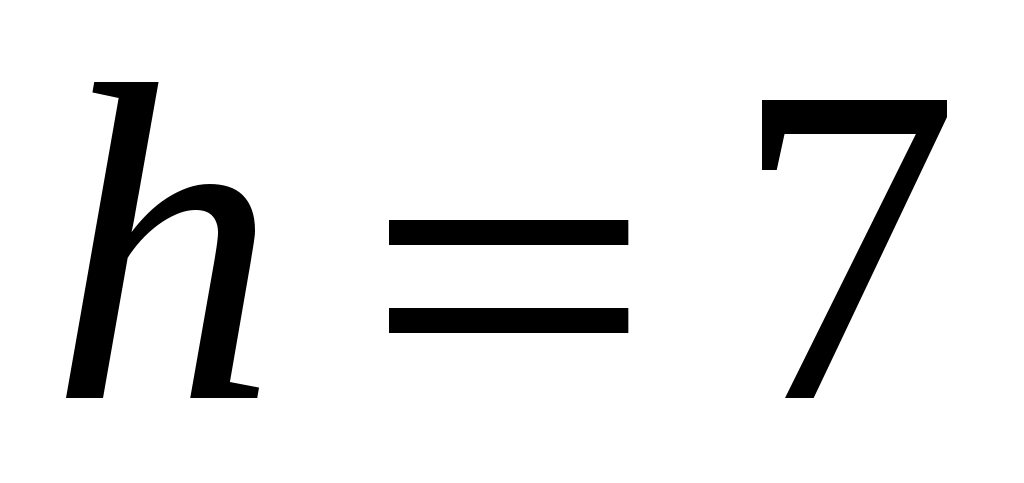 : 285 – 292; 292 – 299; 299 – 306; 306 – 313; 313 – 320; 320 – 327; 327 – 334; 334 – 341; 341 – 348; 348 – 355, и найдём новые частоты : 285 – 292; 292 – 299; 299 – 306; 306 – 313; 313 – 320; 320 – 327; 327 – 334; 334 – 341; 341 – 348; 348 – 355, и найдём новые частоты 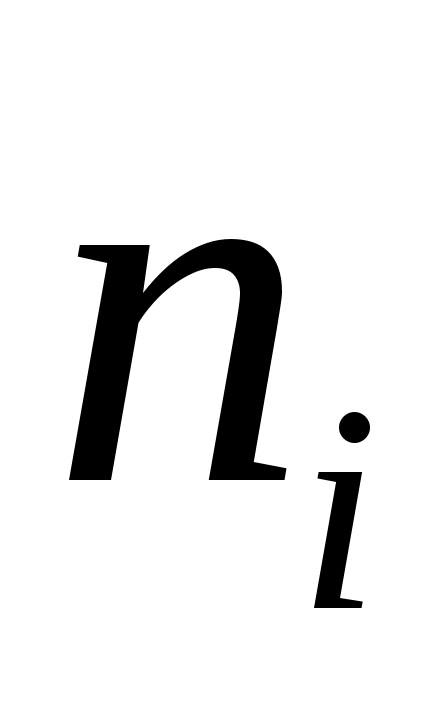 , приняв в качестве их значений сумму частот данных выборки, попавших в i-ый интервал. Итак: , приняв в качестве их значений сумму частот данных выборки, попавших в i-ый интервал. Итак:
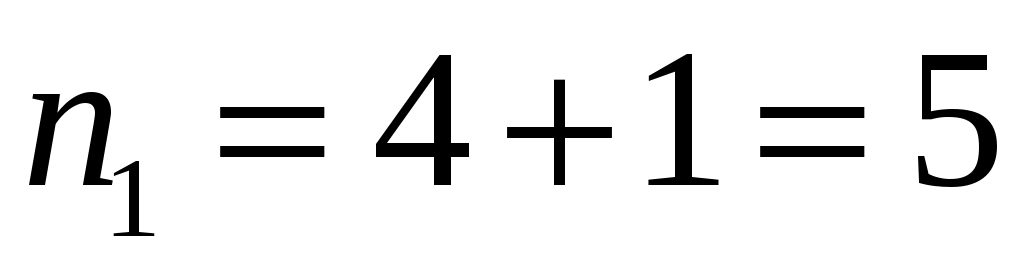 ; ; 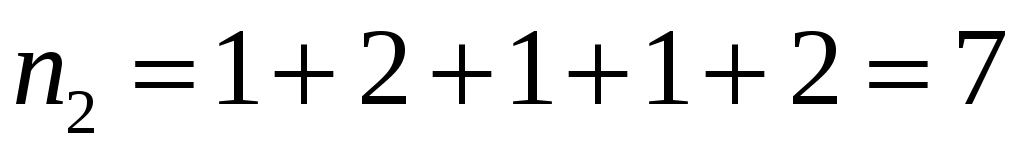 ; ; 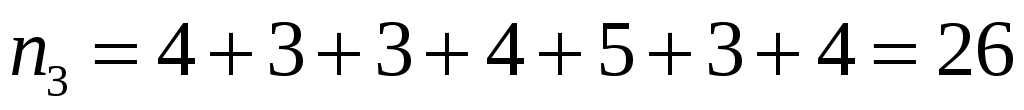 ; ; 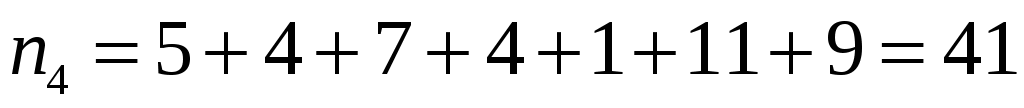 , ,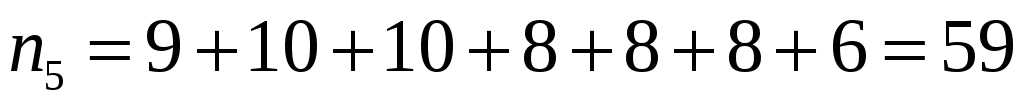 , ,
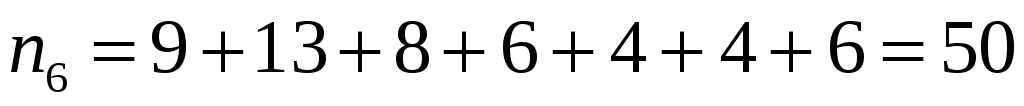 , ,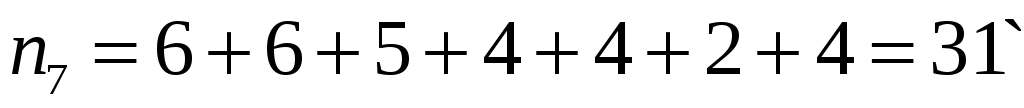 , ,
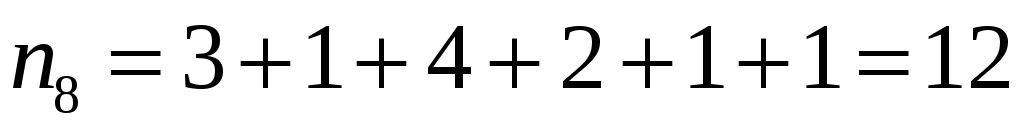 , ,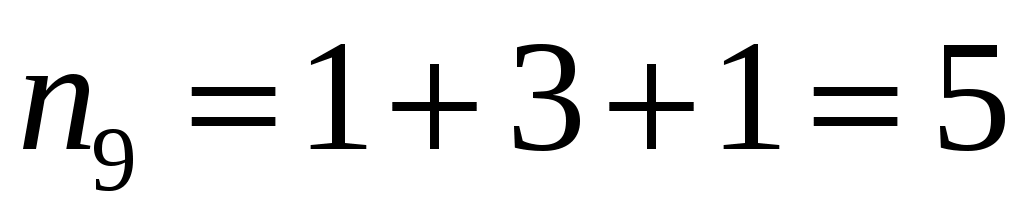 , ,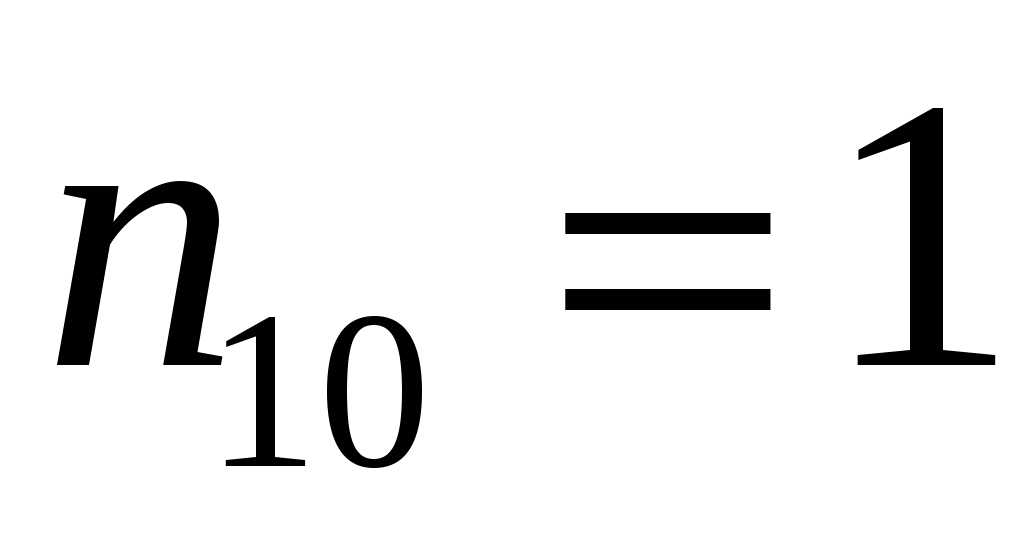
Вычислим плотности частот 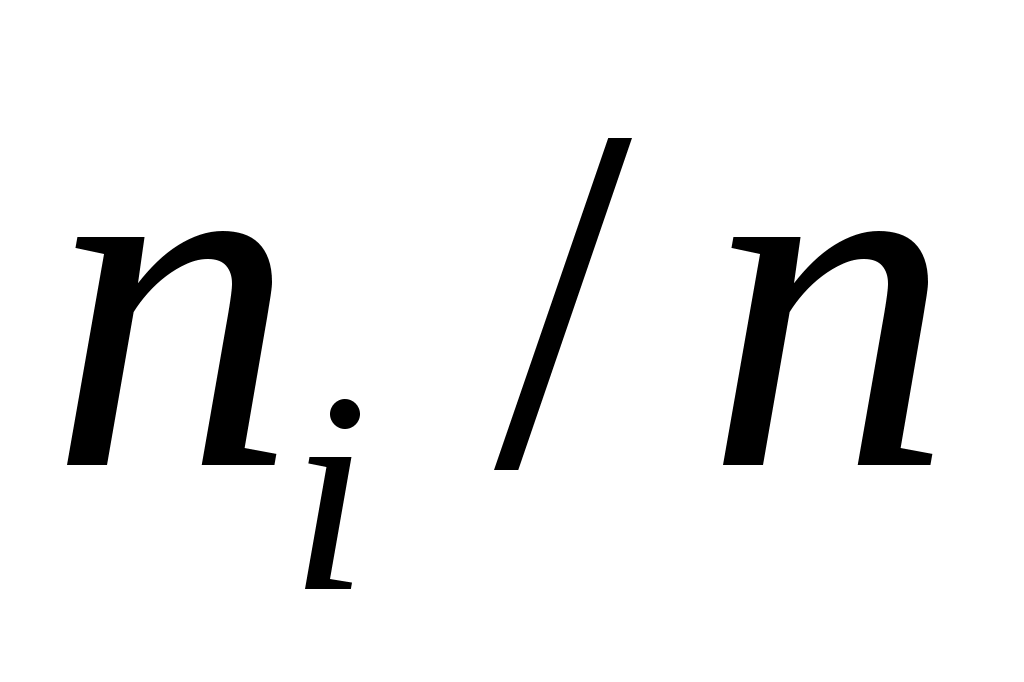 и построим таблицу распределения выборки для построения гистограммы частот: и построим таблицу распределения выборки для построения гистограммы частот:
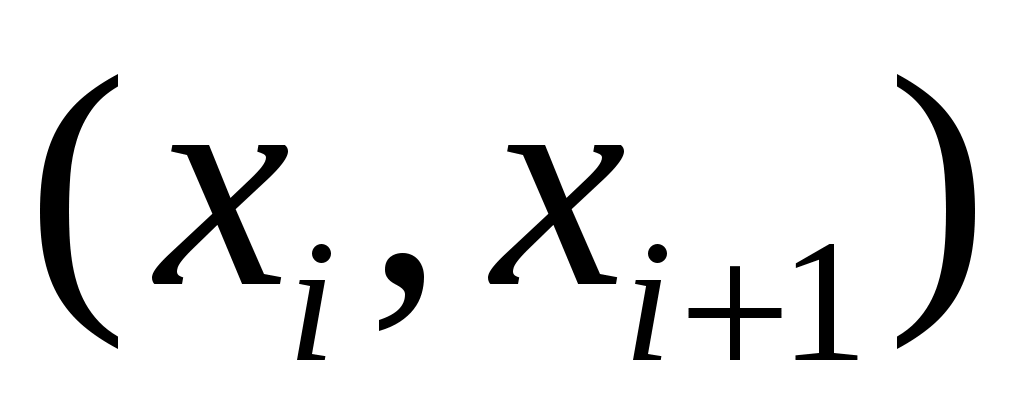
|
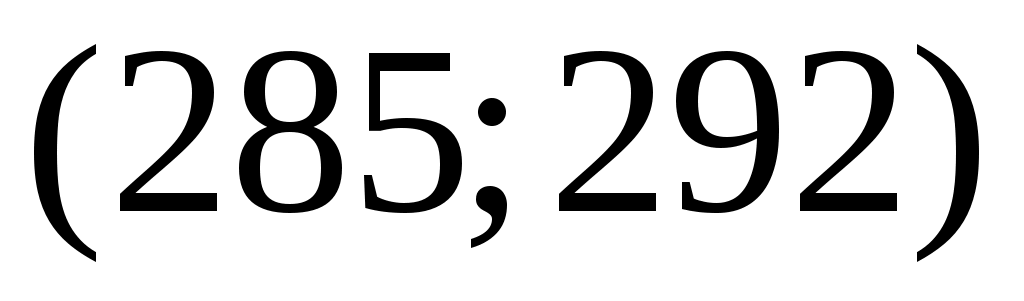
|
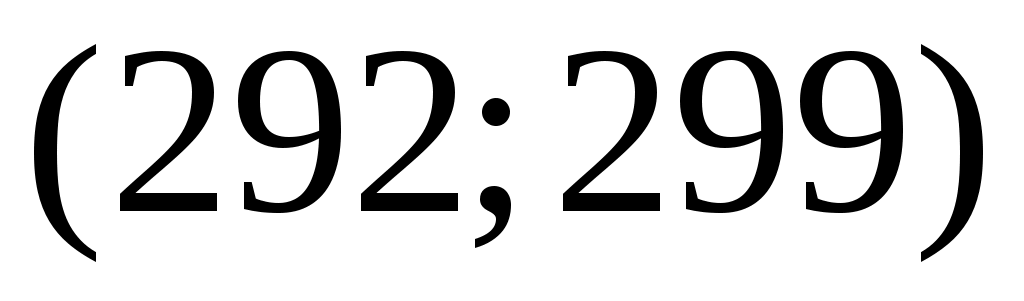
|
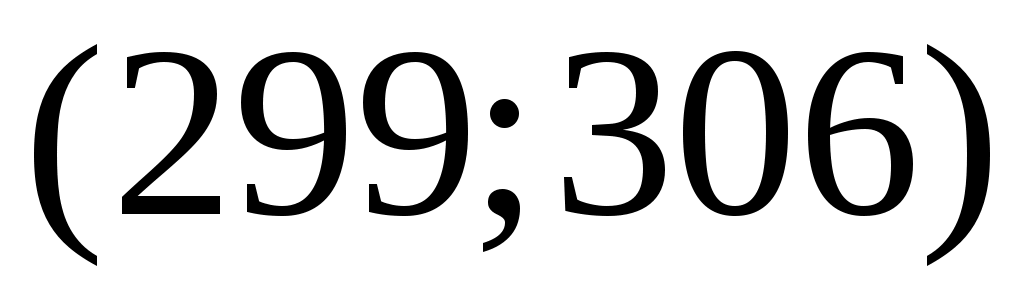
|
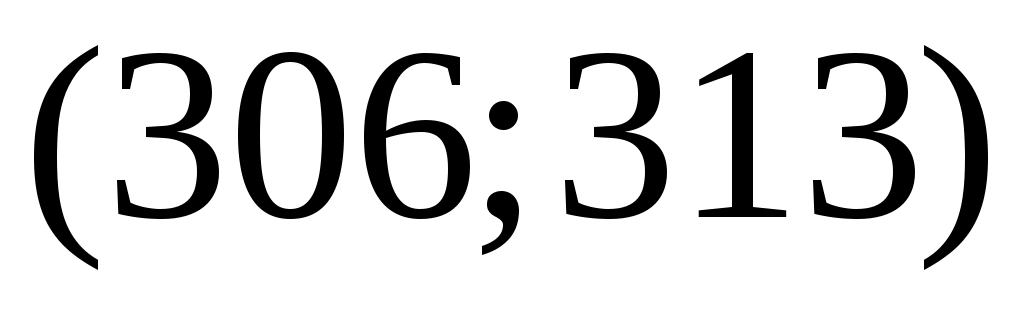
|
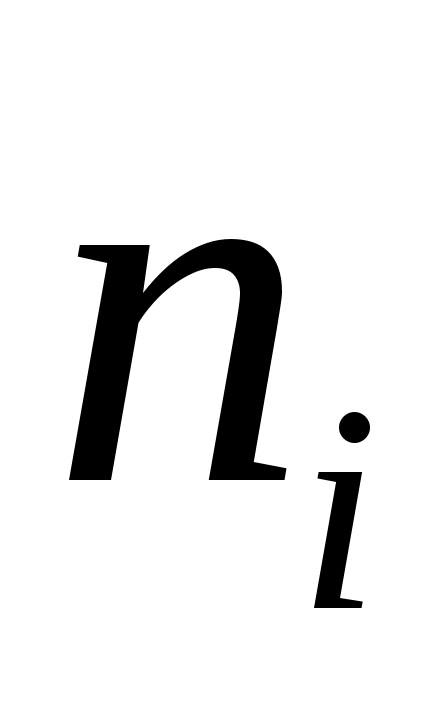
|
5
|
7
|
26
|
41
|
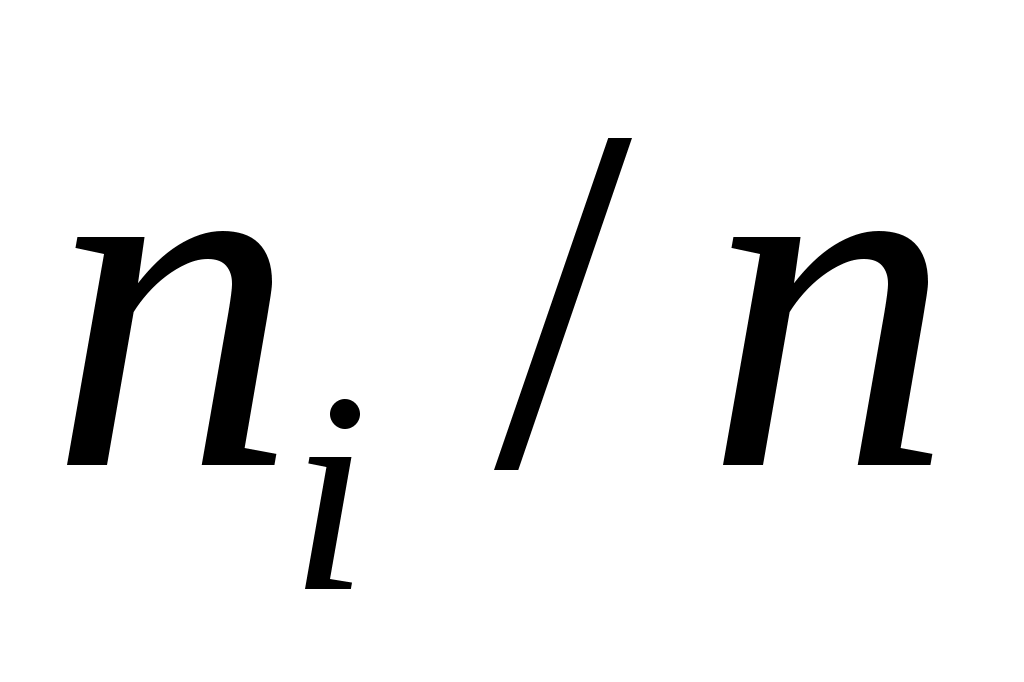
|
0,021
|
0,03
|
0,11
|
0,173
|
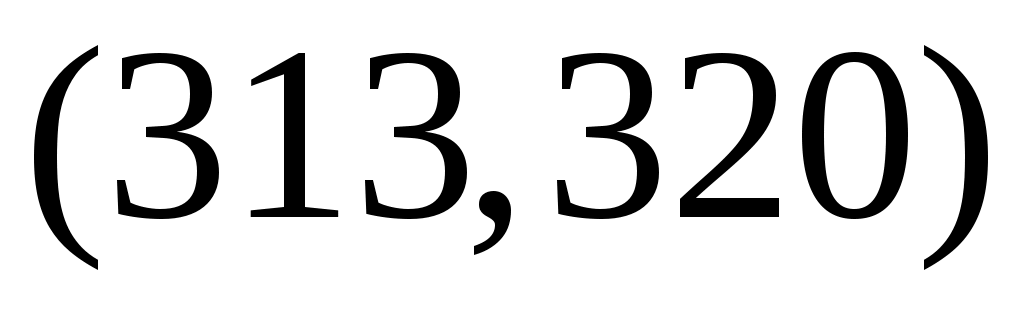
|
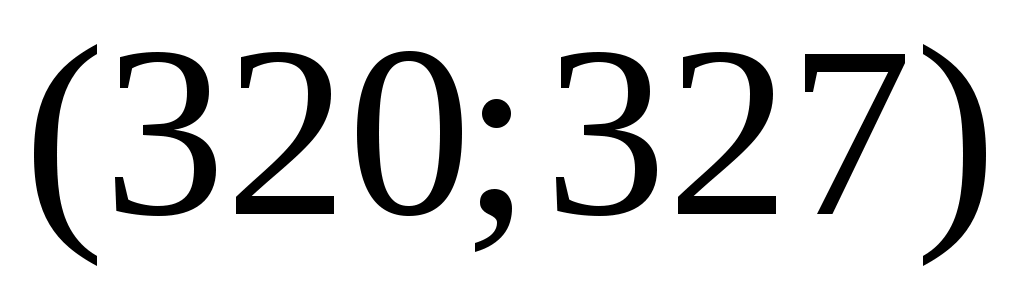
|
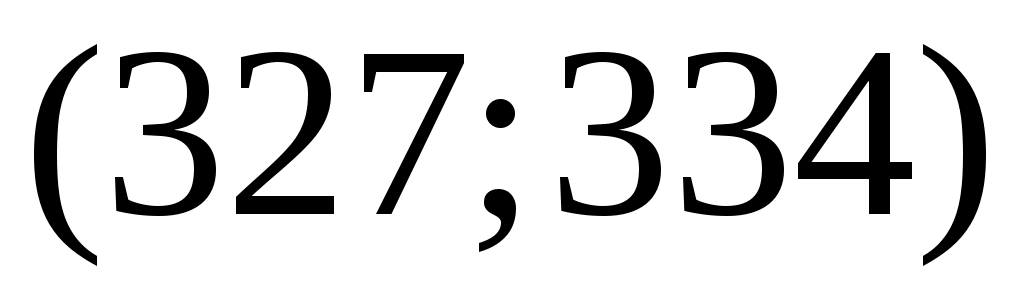
|
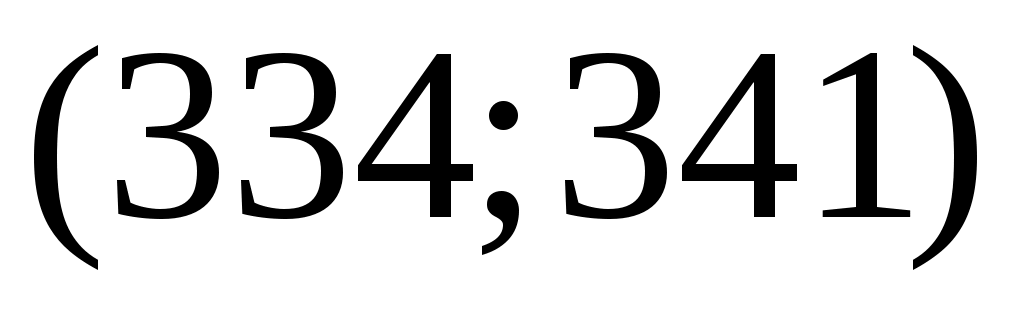
|
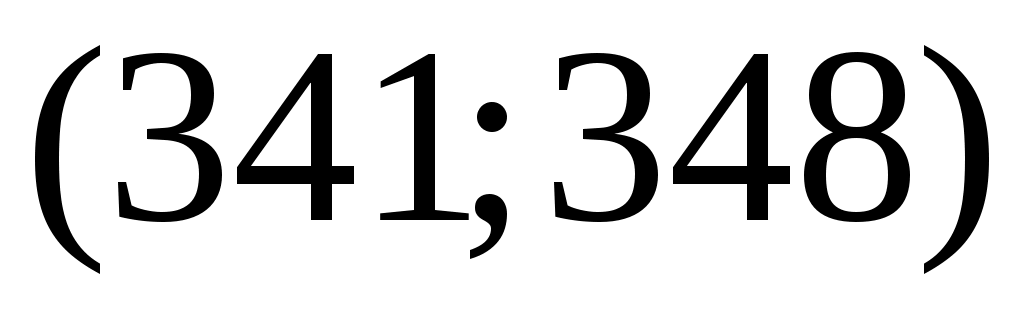
|
59
|
50
|
31
|
12
|
5
|
0,249
|
0,211
|
0,131
|
0,051
|
0,021
|
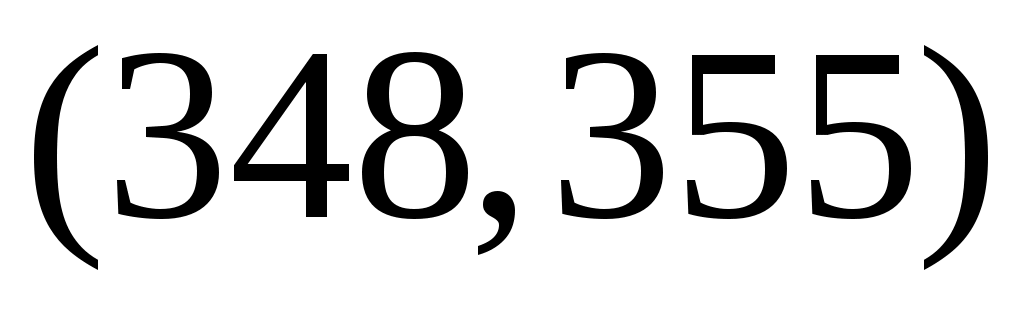
|
1
|
0,004
|
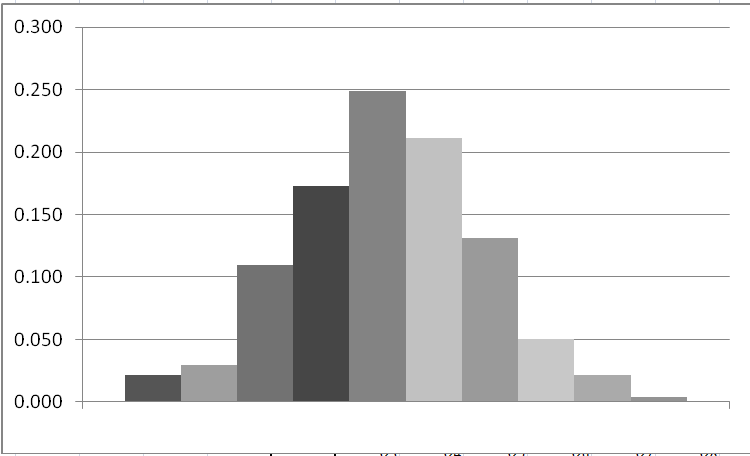
Гистограмма частот изображена на рисунке:
Рисунок
2. Приняв в качестве новых вариант 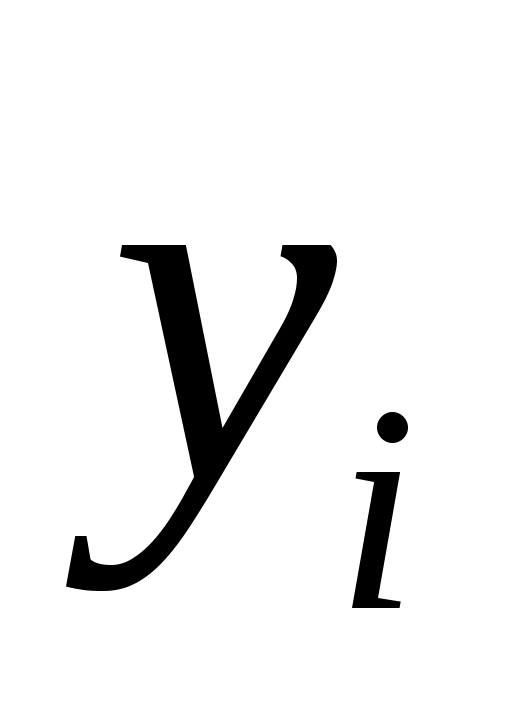 серединные значения частичных интервалов серединные значения частичных интервалов 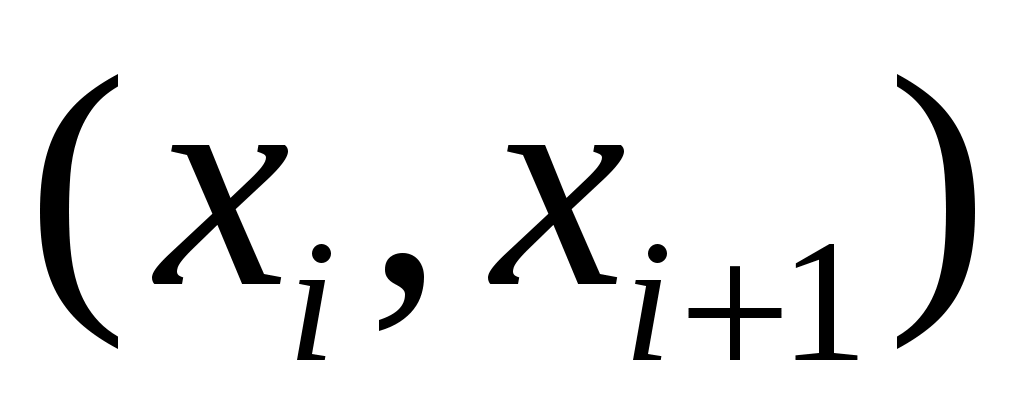 , построим распределение равноотстоящих вариант для вычисления точечных оценок генеральной средней и дисперсии методом произведений. , построим распределение равноотстоящих вариант для вычисления точечных оценок генеральной средней и дисперсии методом произведений.
Напомним процедуру вычисления оценок генеральной средней и дисперсии по методу произведений.
Выберем 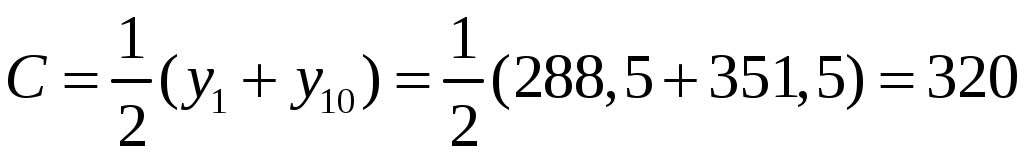 . .
Вычислим 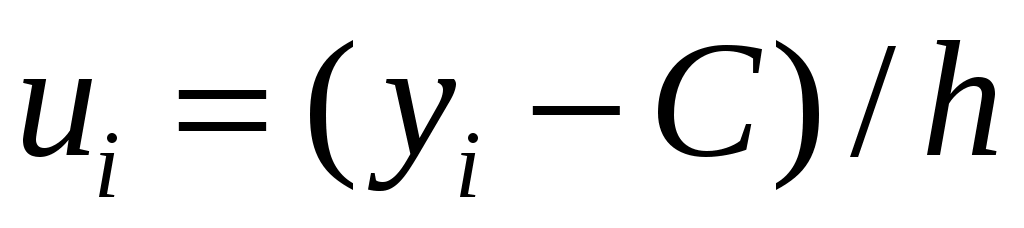 – условные варианты. – условные варианты.
Найдём 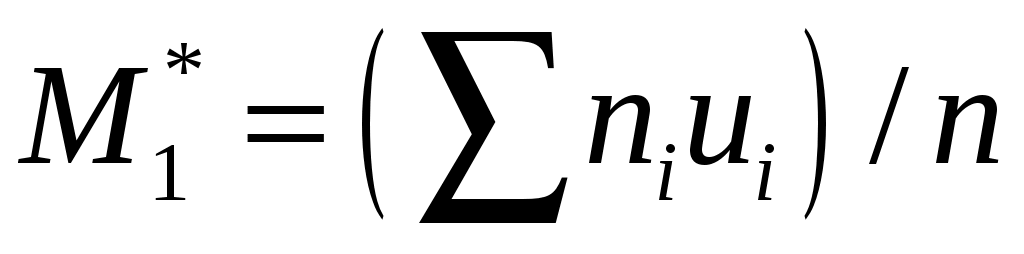 – условный момент первого порядка, – условный момент первого порядка,
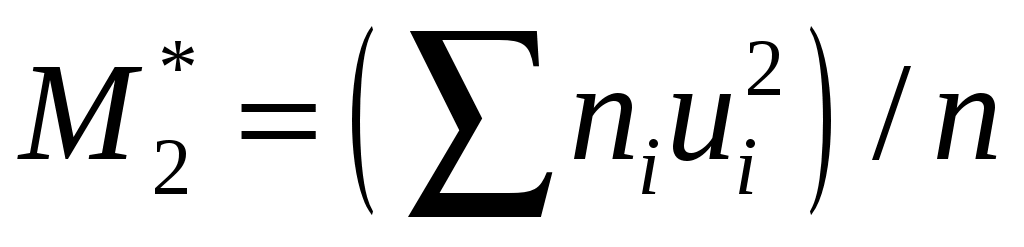 – условный момент второго порядка. – условный момент второго порядка.
Тогда:
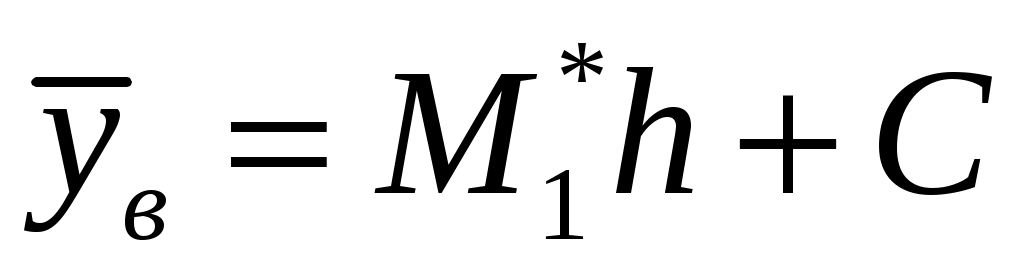 – выборочная средняя, – выборочная средняя,
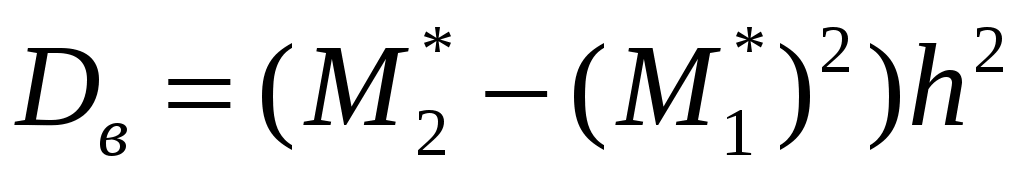 – выборочная дисперсия. – выборочная дисперсия.
Результаты вычислений сведём в таблицу:
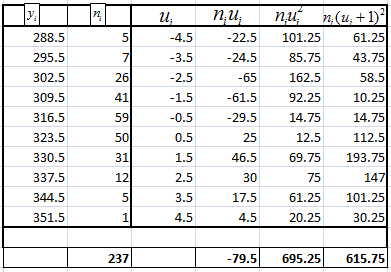
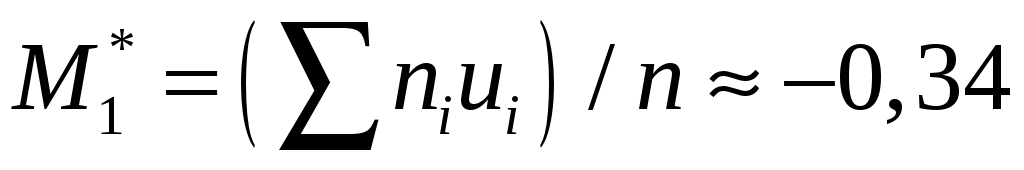 ; ; 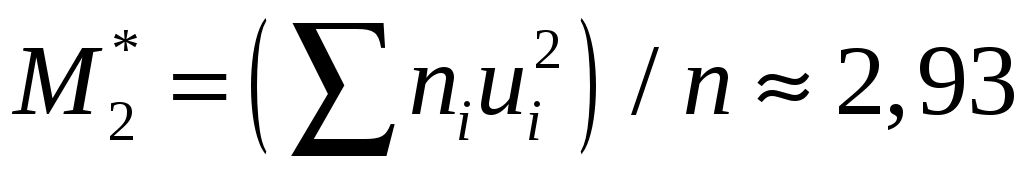 ; ;
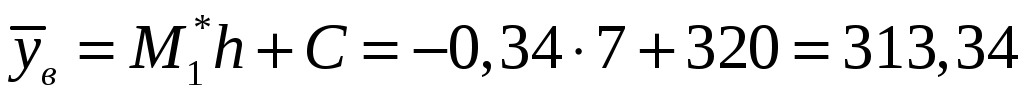 ; ;
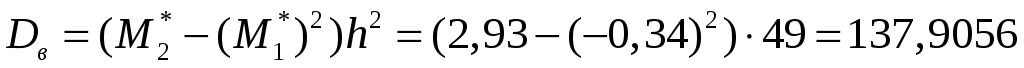 . .
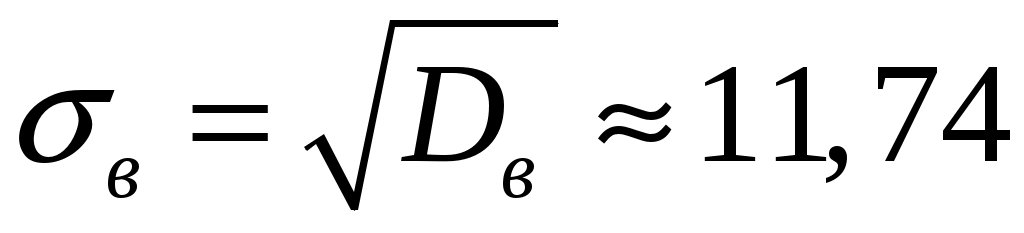 . .
3. Для получения интервальной оценки математического ожидания  нормально распределённой случайной величины по выборочной средней нормально распределённой случайной величины по выборочной средней 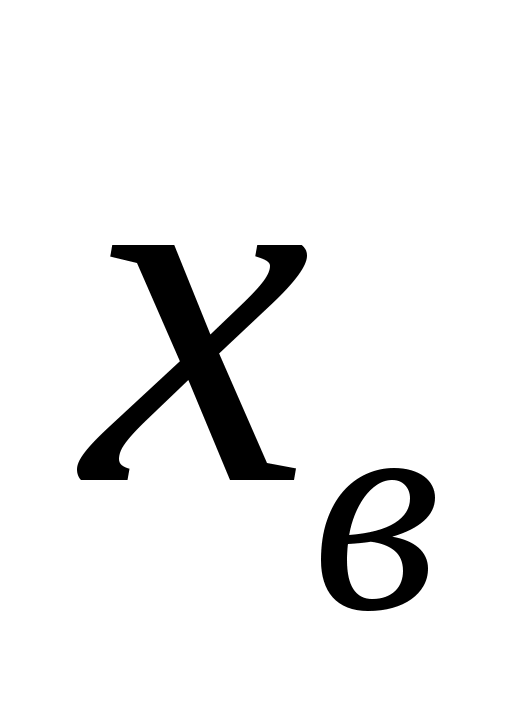 и неизвестной дисперсии используем формулу: и неизвестной дисперсии используем формулу:
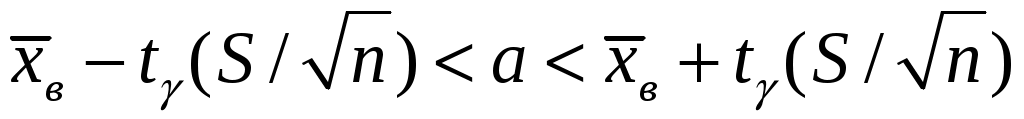 , ,
где 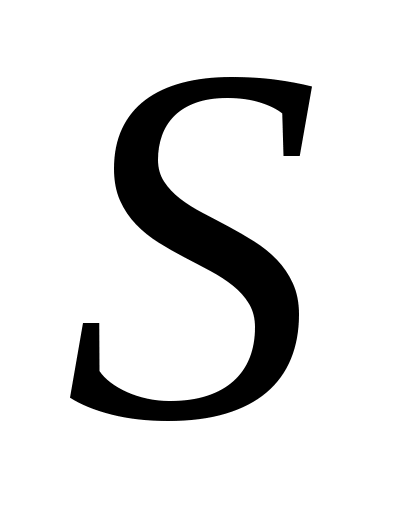 – «исправленное» выборочное средне квадратическое отклонение, – «исправленное» выборочное средне квадратическое отклонение, 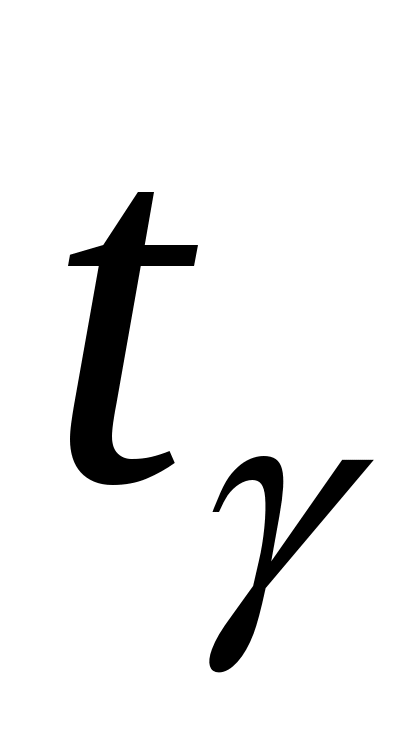 – случайная величина распределённая по закону Стьюдента с числом степеней свободы – случайная величина распределённая по закону Стьюдента с числом степеней свободы 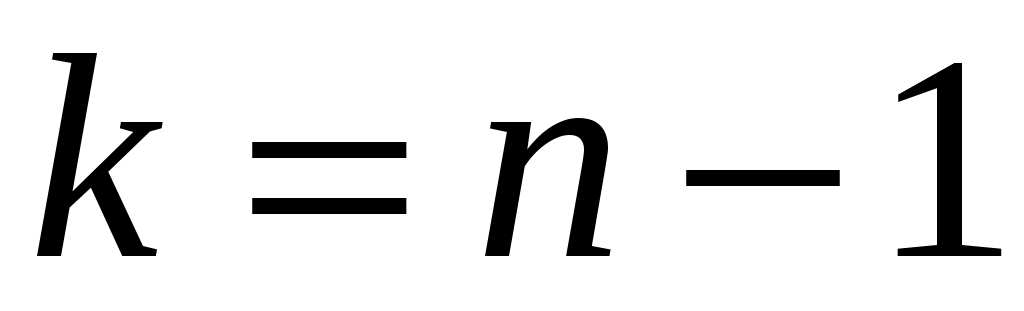 (находится по таблице при заданных (находится по таблице при заданных 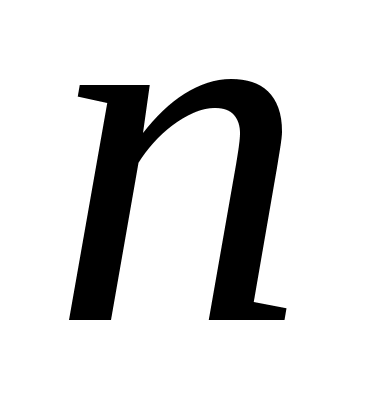 и и 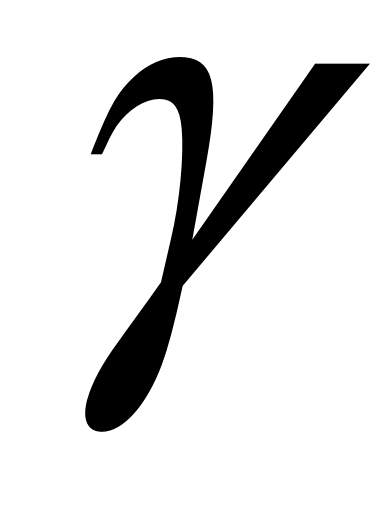 ). ).
Найдём 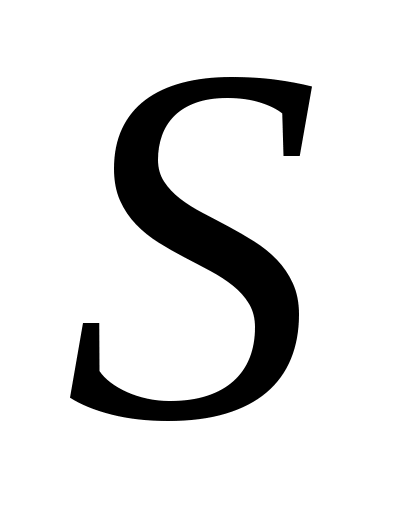 . .
Имеем 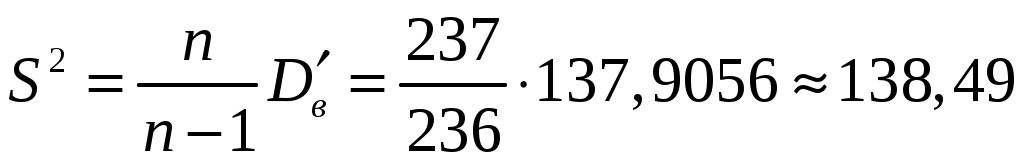 . .
Отсюда 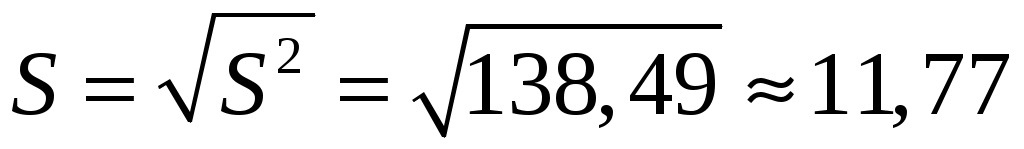 . При . При 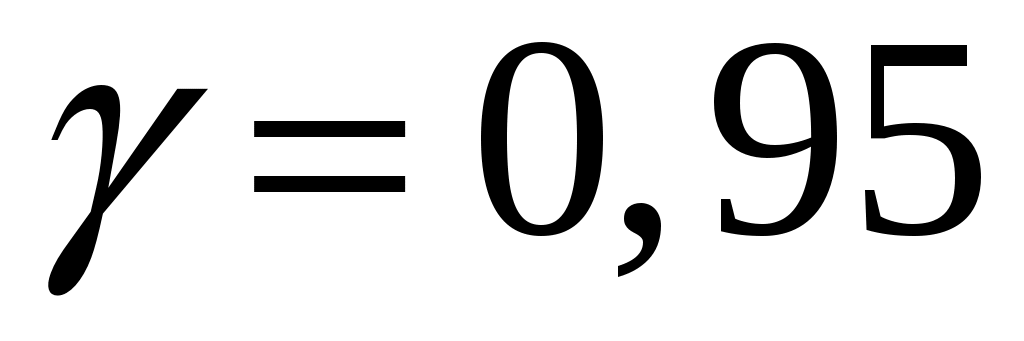 и и 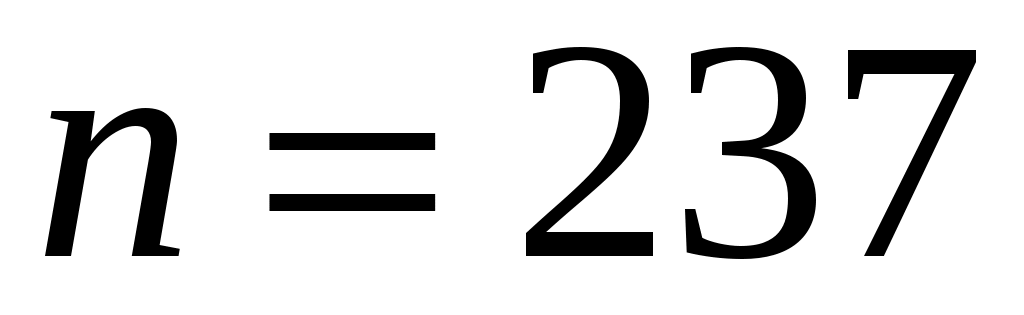 имеем имеем 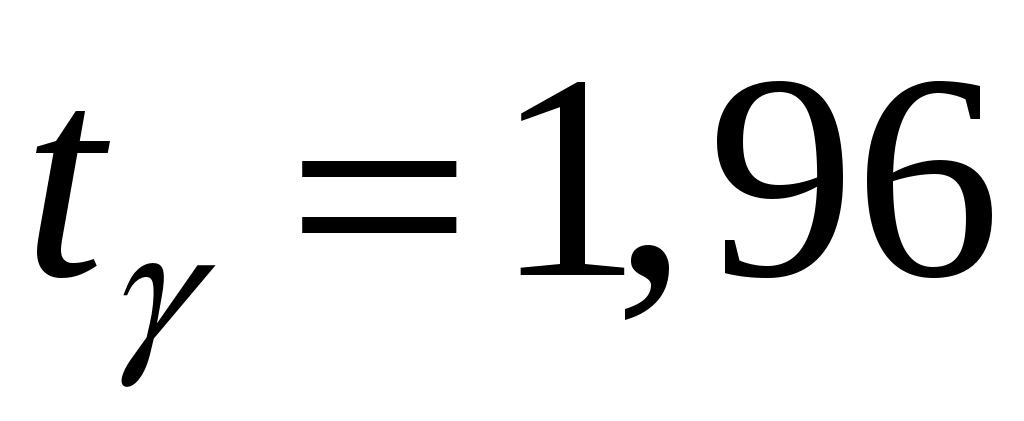 и и 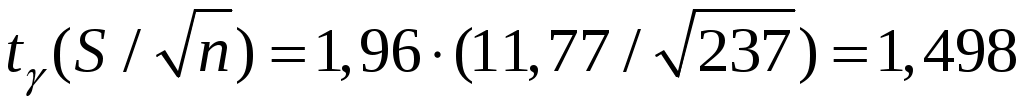 . Тогда доверительный интервал для математического ожидания равен: . Тогда доверительный интервал для математического ожидания равен:
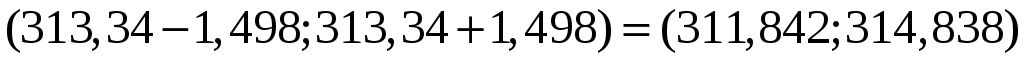 . .
Для получения интервальной оценки дисперсии нормальной генеральной совокупности используют случайную величину 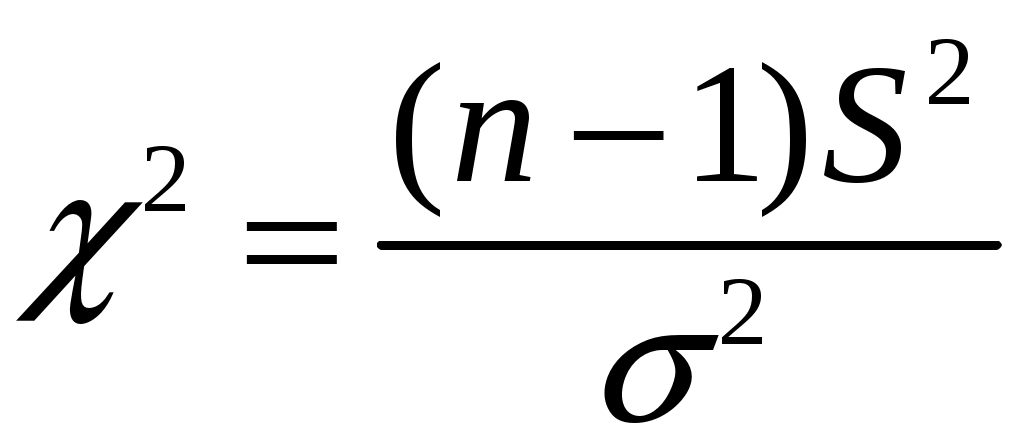 . Величина . Величина 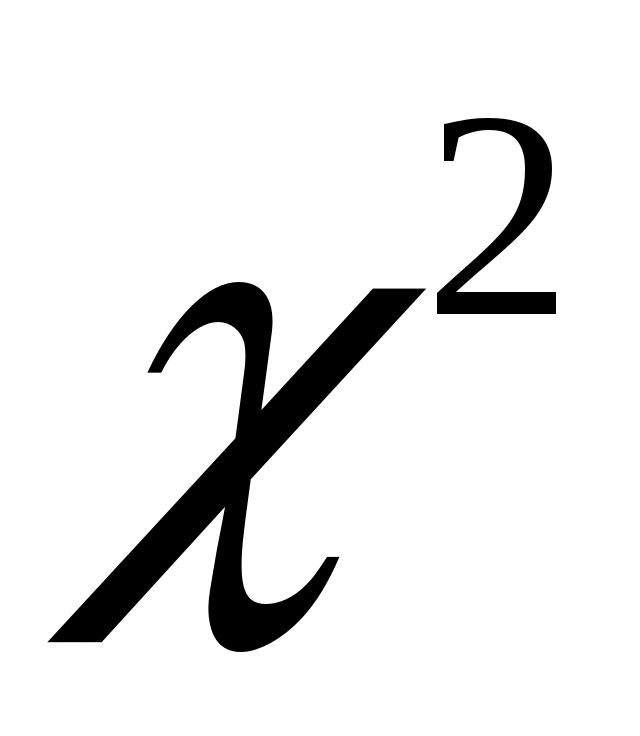 имеет распределение Пирсона с числом степеней свободы имеет распределение Пирсона с числом степеней свободы 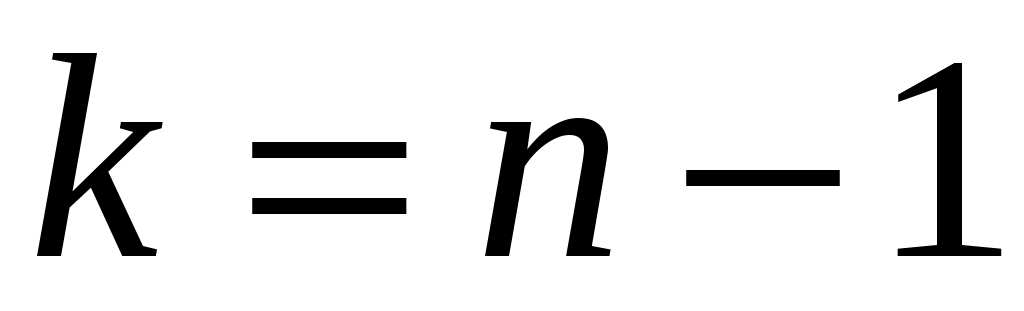 и представлена в таблицах. По этим таблицам определяются два числа (критические точки распределения и представлена в таблицах. По этим таблицам определяются два числа (критические точки распределения 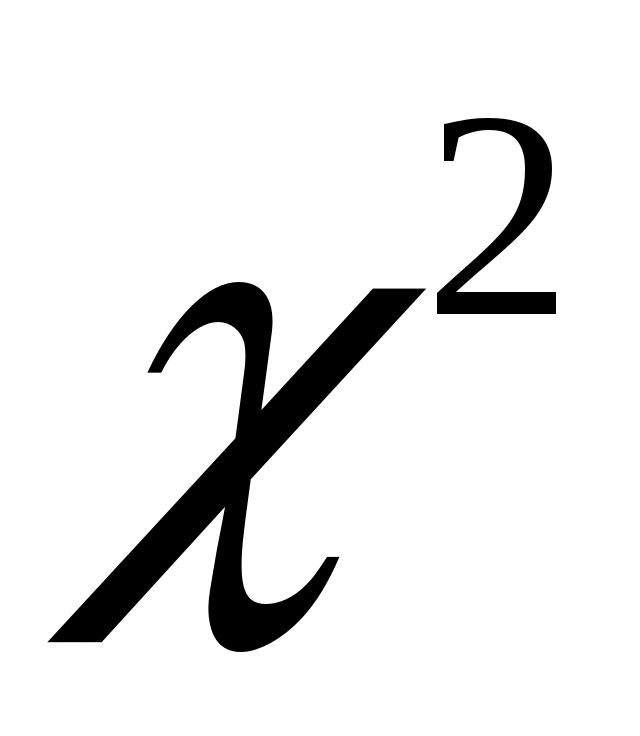 ) )  и и 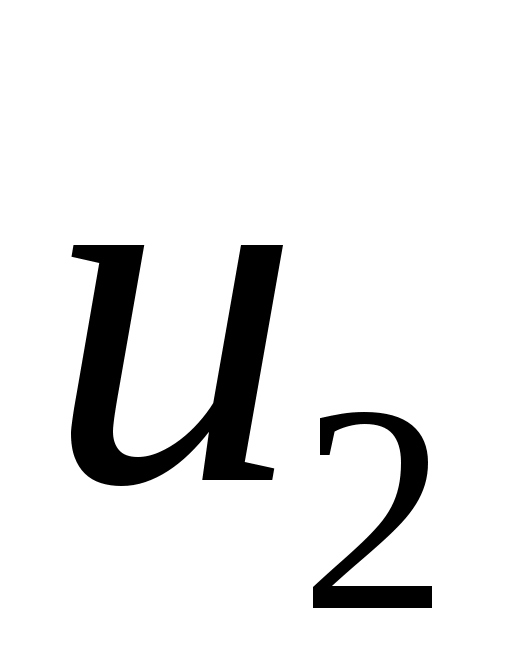 : :
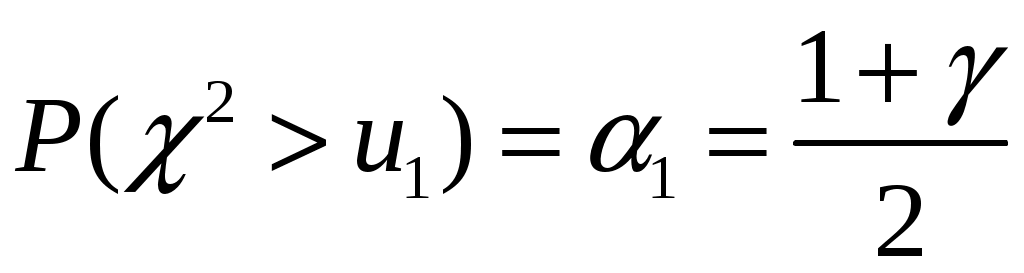 , , 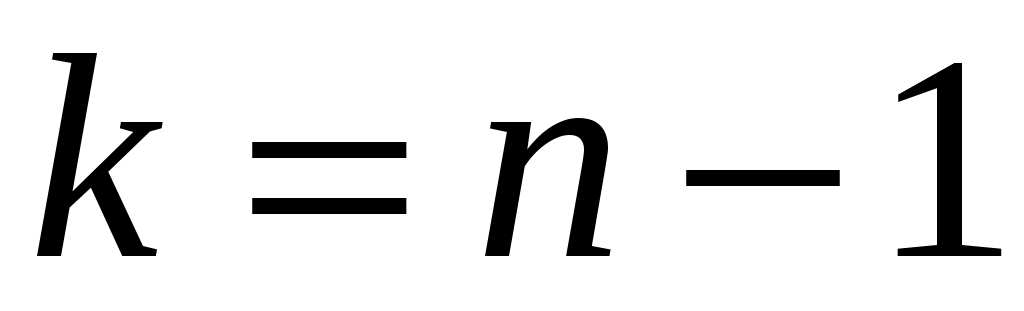 ; ;
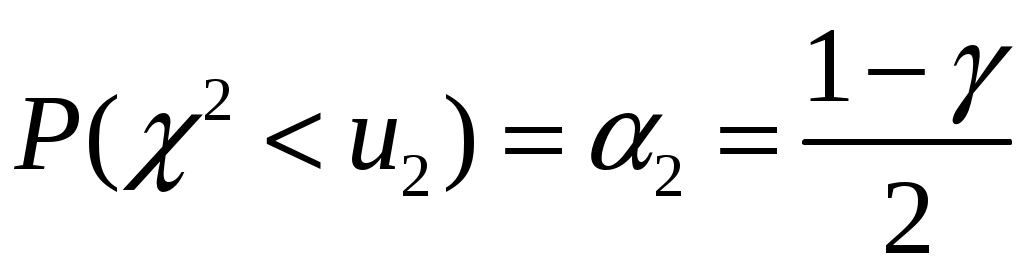 , , 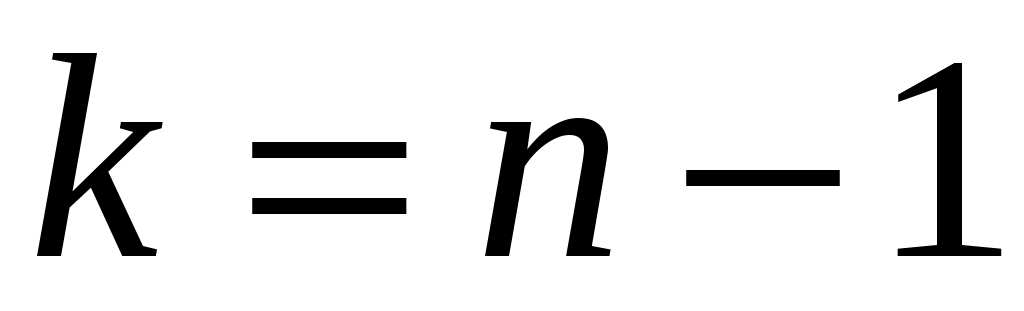 . .
|
 Скачать 0.85 Mb.
Скачать 0.85 Mb.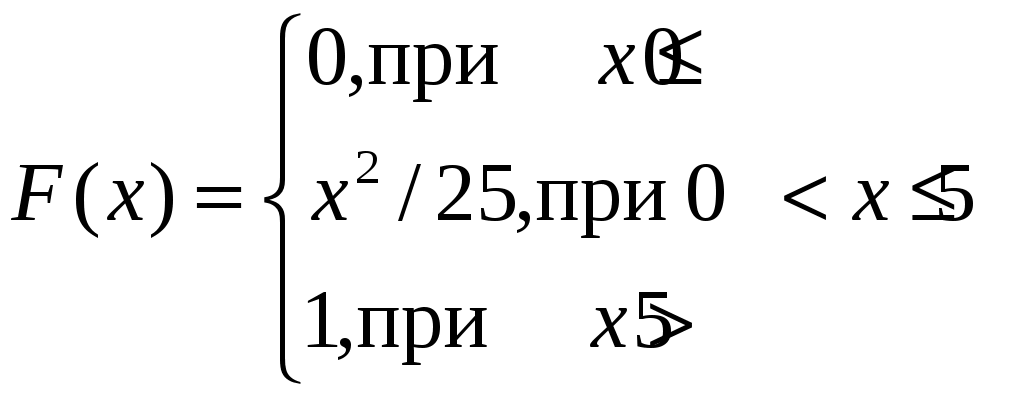 .
.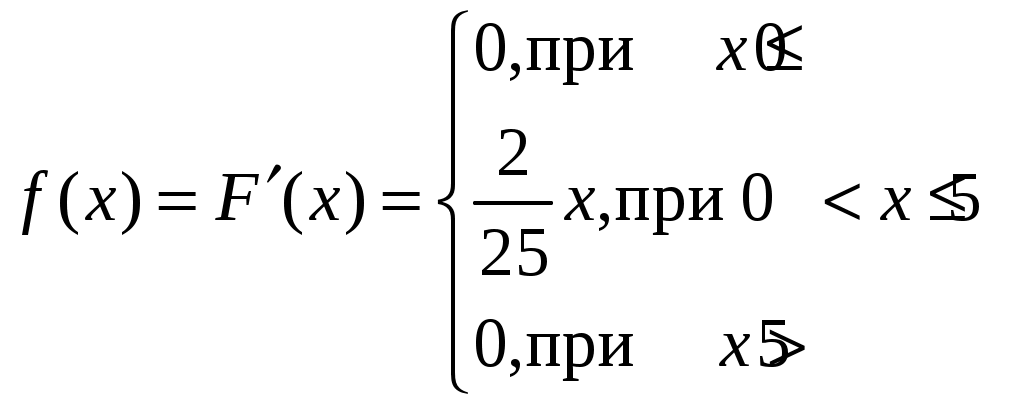 .
.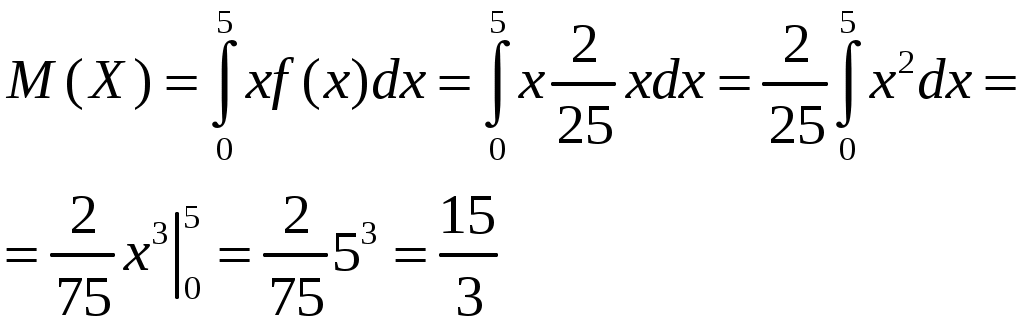 ,
,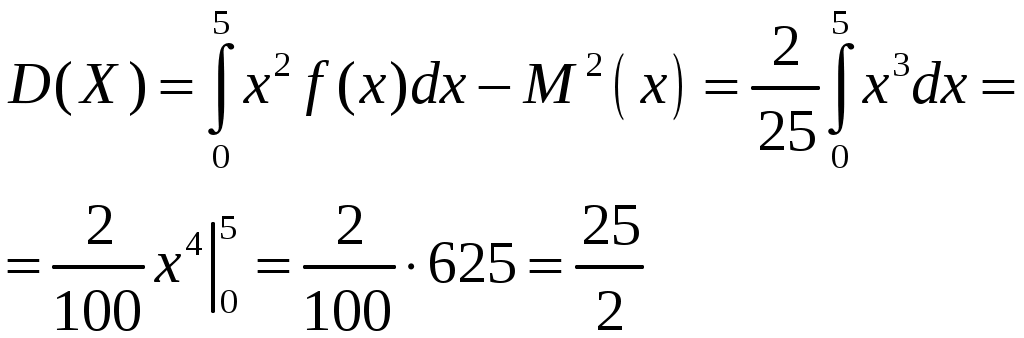 .
.

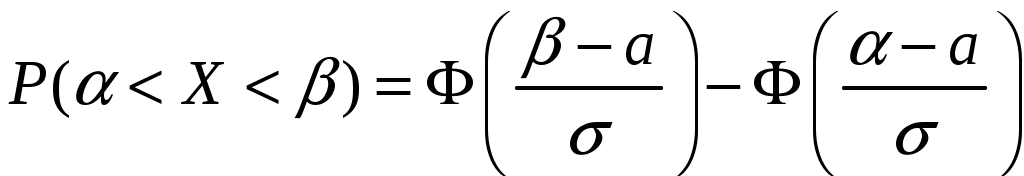 ,
,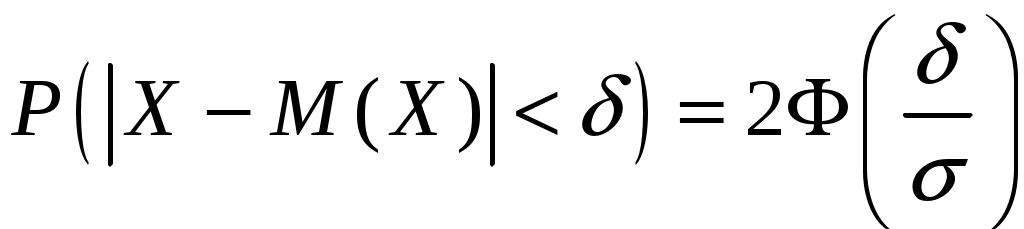 .
.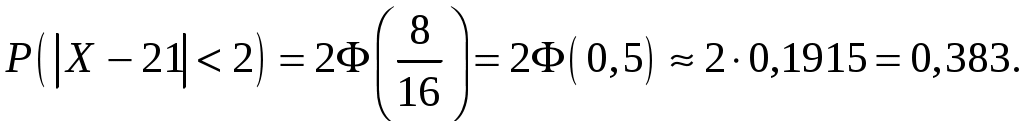

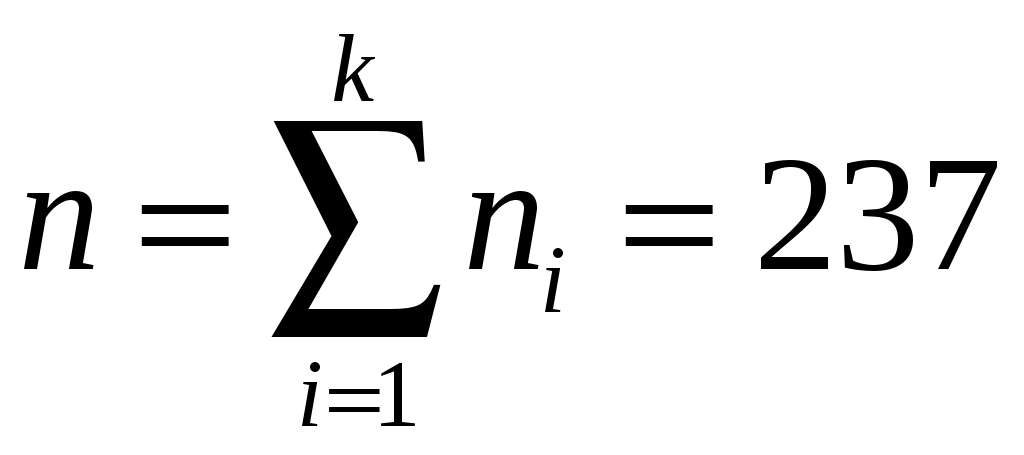 – объём выборки.
– объём выборки.

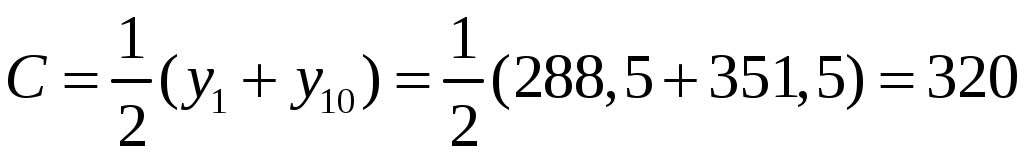 .
.
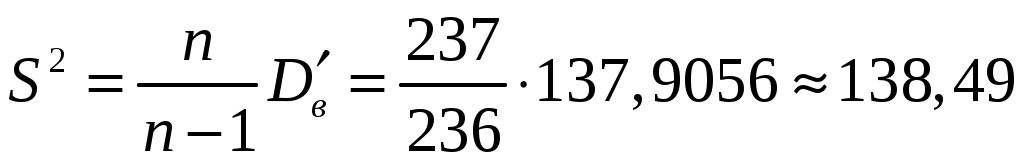 .
.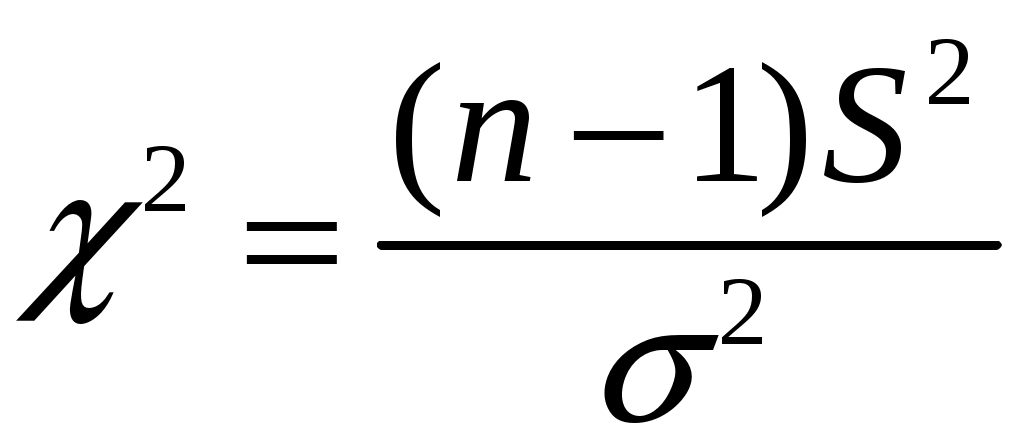 . Величина
. Величина 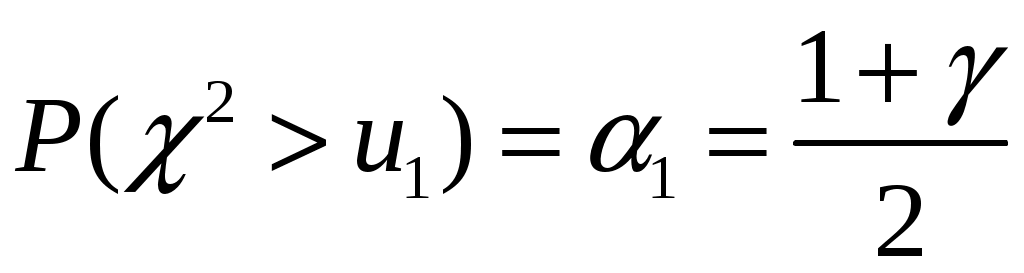 ,
, 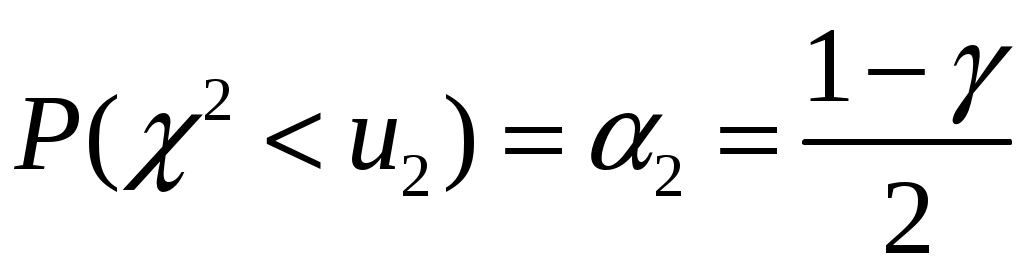 ,
, 