Задача 1 Вычислить двойной интеграл от функции по заданной области . Решение Вид области представлен на рисунке

• Название: Задача 1 Вычислить двойной интеграл от функции по заданной области . Решение Вид области представлен на рисунке
• Дата: 22.05.2023
• Размер: 0.85 Mb.
• Имя файла: 800.doc
• Тип: Задача; #1152069
• страница: 3 из 3

Замечание Если число степеней свободы 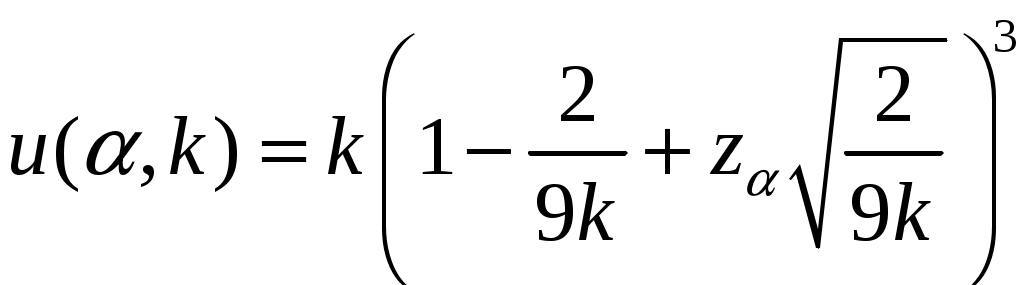, то критическую точку можно найти из равенства Уилсона-Гильферти:

,

где находят из равенства , используя функцию Лапласа.

Тогда доверительный интервал для дисперсии можно записать в виде: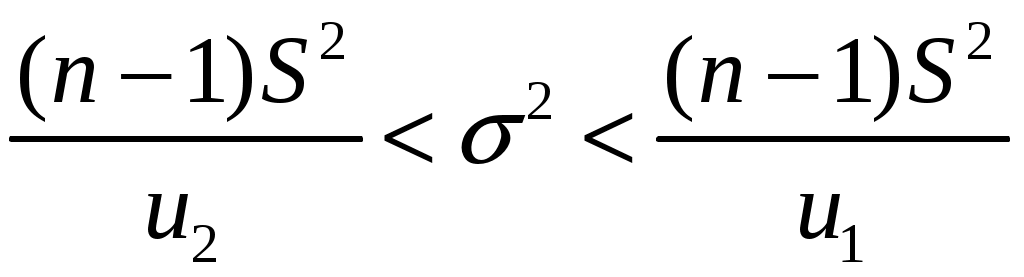

.

В нашей задаче по условию 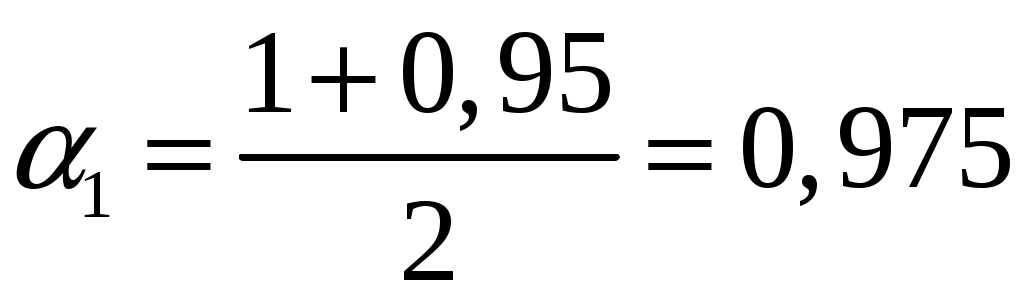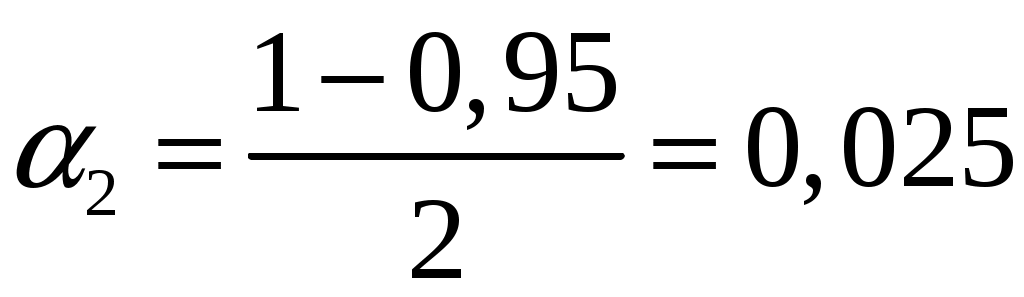. Тогда, ; ; .

Так как в нашем случае 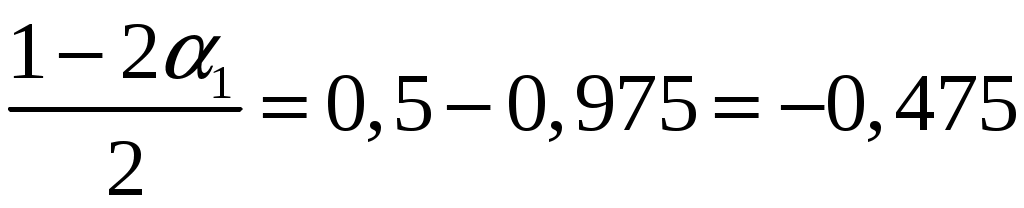используем равенство Уилсона-Гильферти для нахождения и :

; ;

из равенства 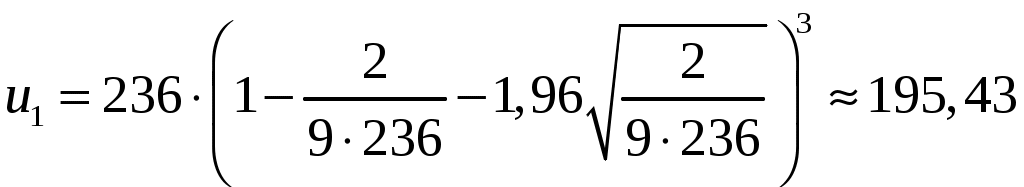находим . Тогда:

.

Аналогично: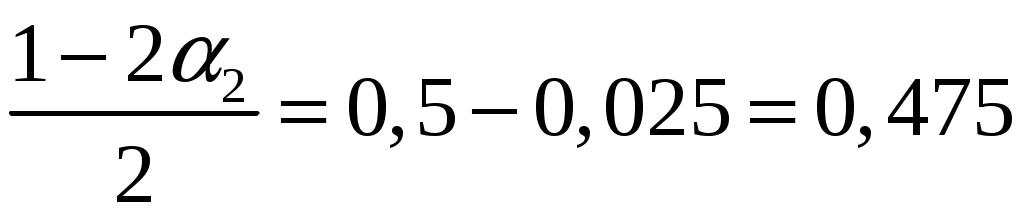

; ;

из равенства 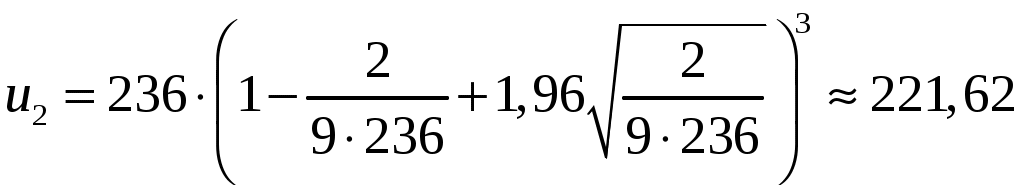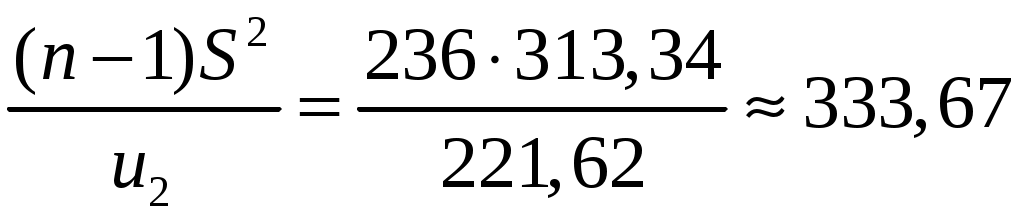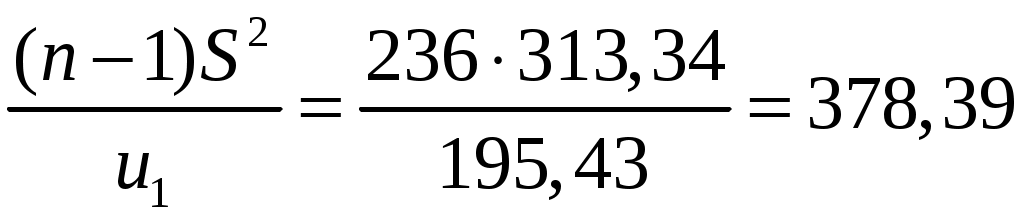находим . Тогда:

;

; .

Таким образом, доверительный интервал для дисперсии:

.

4. Считаем, что эмпирическое распределение задано в виде последовательности интервалов и соответствующих им частот:

	5	7	26	41

59	50	31	12	5

1

Перейдём к новой случайной величине: и вычислим концы интервалов , полагая , , ; ; , ,

, ,

, ,



Найдём теоретические вероятности попадания случайной величины в интервал , здесь  – функция Лапласа.

;



.













Проверка: .
Вычислим теоретические частоты :

; ;

; ,

, ,

, ,

, .

Найдём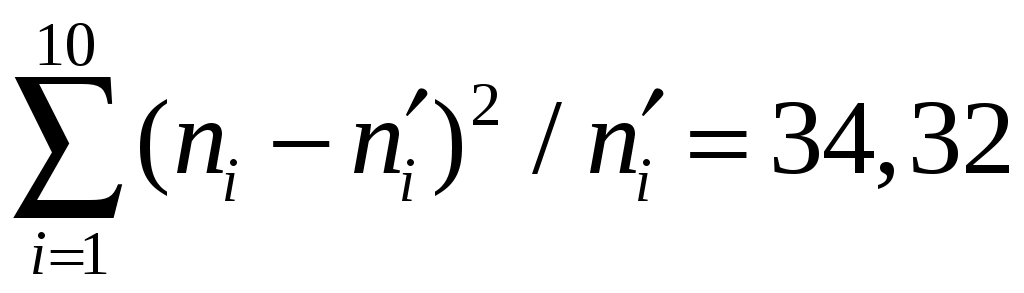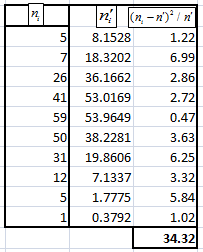


.

По таблице критических точек распределения , по заданному уровню значимости и числу степеней свободы , (где  – число интервалов выборки) находим критическую точку правосторонней критической области: . Так как , то гипотезу о нормальном распределении генеральной совокупности отвергаем.