Задачи. Гидравлика-задачи. Задача 1 Задача 2 Задача 3
 Скачать 1.52 Mb. Скачать 1.52 Mb.
|
|
СОДЕРЖАНИЕ Задача 1…………………………………………………………………….....2 Задача 2……………………………………………………………………….3 Задача 3…………………………………………………………………….....4 Задача 4……………………………………………………………………….6 Задача 5…………………………………………………………………….....8 Задача 6……………………………………………………………………….9 Задача 7……………………………………………………………………...10 Задача 8……………………………………………………………………...11 Задача 9……………………………………………………………………...13 Литература………………………………………………………………….15 Задача 1 Какое давление больше: N или M ? Исходные данные: N = 6 м вод. ст M = 300 мм рт.ст Решение Зависимость между единицами давления: 1,012·105Па = 760 мм рт. ст. = 1,033·104 мм вод. ст. Переведем значение давления к Па: N = 6 м вод. ст. = 6·103 мм вод. ст. 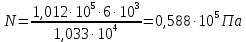 M = 300 мм рт.ст. 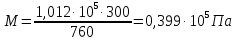 Сравнивая значения видим, что давление N больше давления M. Задача 2 Два горизонтальных цилиндрических трубопровода А и В содержат соответственно минеральное масло плотностью 900 кг/м3 и воду плотностью 1000 кг/м3. Высоты жидкостей, представленные на рисунке 1, имеют следующие значения: hм, hрт; hв. Зная, что гидростатическое давление на оси трубопровода А равно pА, определить давление на оси трубопровода В pВ 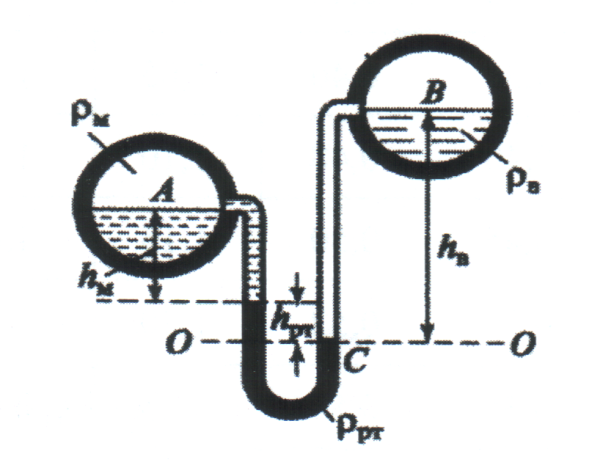 Рисунок 1 Исходные данные: hм = 0,35м hрт = 0,46м; hв = 1,05м; РА = 1,2 ·105 Па; РВ = ? Решение Составим уравнение равновесия относительно нижней линии раздела между водой и ртутью ОО: 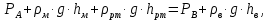 где ρрт = 13600 кг/м3 – плотность ртути Из этого уравнения определяем давление на оси трубопровода В 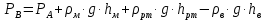 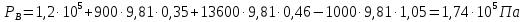 Задача 3 Определить давление масла p1, подводимого в поршневую полость гидроцилиндра, если избыточное давление в штоковой полости p2, усилие в штоке R, сила трения в подвижных сочленениях Fтр = 1,1 кН, диаметр поршня D = 125мм, диаметр штока d = 70мм(рисунок 2) 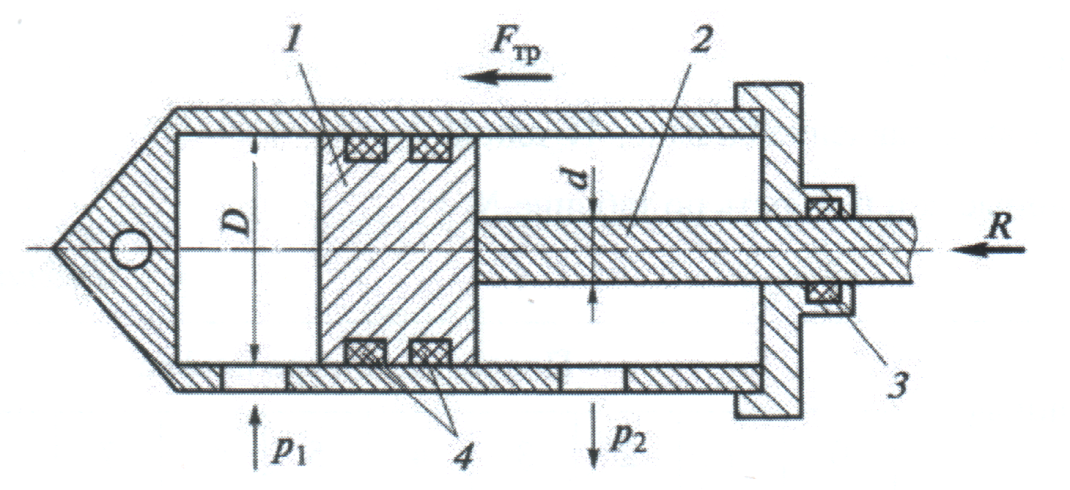 Рисунок 2 Исходные данные: р2 = 86 кПа; R = 21,50кН р1 = ? Решение Давление р1 находим из условия равновесия поршня, на который , кроме силы R, действуют силы давления и сила трения, направленная против перемещения поршня. Силы давления: 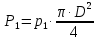 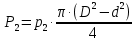 Уравнение равновесия: 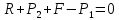 либо 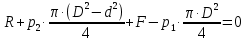 Отсюда находим р1 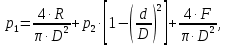 где R = 21,50кН = 21500Н, Fтр = 1,1 кН = 1100Н, р2 = 86 кПа = 86 ·103 Па, D = 125мм = 0,125м, d = 70мм = 0,04м 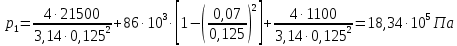 Задача 4 Определить средние скорости, смоченные периметры и гидравлические радиусы в сечениях постепенно расширяющегося трубопровода, где диаметры D1 = 100 мм, D2 = 150 мм, D3 = 220 мм при расходе Q. Исходные данные: Q = 8 л/с Решение При установившемся движении жидкости расход через все живые сечения 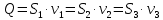 , ,где Q = 8 л/с = 8 · 10-3 м3/с; 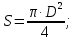 D1 = 100 мм = 0,100м, D2 = 150 мм = 0,150м, D3 = 220 мм = 0,220м 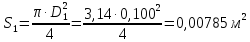 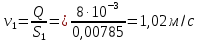 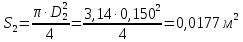 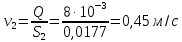 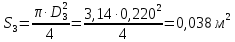 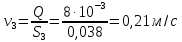 Отношение площади живого сечения S к смоченному периметру П называется гидравлическим радиусом 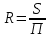 Для круглой трубы при напорном течении, 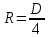 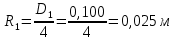 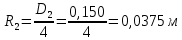 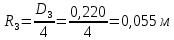 Смоченный периметр 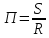 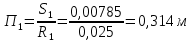 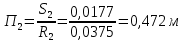 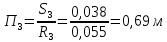 Задача 5 Определить давление p1 в сечении 1-1 горизонтально расположенного сопла гидромонитора (рисунок 3), необходимое для придания скорости в воде в выходном сечении 2-2 υ2, если скорость движения воды в сечении 1-1 υ1.  Рисунок 3 Исходные данные: v1 = 2,5м/с; v5 = 25м/с; Р1 = ? Решение За расчетные сечения выбираем сечения 1-1 и 2-2, в которых скорости заданы, давление p1 подлежит определению, а давление p2 в сечении на выходе из гидромотора равно атмосферному. Плоскость сравнения следует провести через ось сопла, тогда удельные энергии положения z1 = z2 = 0 и уравнение Д. Бернулли будет иметь следующий вид: 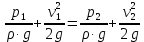 откуда 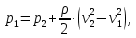 где р2 = 1,012 ·105 Па – атмосферное давление; ρ = 1000кг/м3 – плотность воды 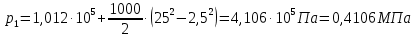 Задача 6 Трубка полного давления помещена в поток жидкости, движущейся в открытом канале (рисунок 4). Жидкость поднялась в трубке на высоту ∆h = 0,4м. на какую высоту поднимается жидкость в трубке, если скорость движения жидкости увеличится в два раза?  Рисунок 4 Решение Высота Δh, показанная на рисунке, определяет скоростной напор потока и может быть вычислена, м: 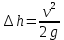 Из этой формулы определяем скорость потока 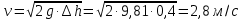 Если скорость движения жидкости увеличится в два раза, т.е v = 2 · 2,8 = 5,8м/с определим высоту Δh 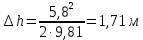 Задача 7 Определить режим течения керосина в трубопроводе диаметром d, при известном расходе. Исходные данные: Q = 60 кг/с; d = 90мм Решение Определяем режим течения керосина, 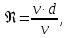 где Re – критерий Рейнольдса; ρ – плотность керосина, кг/м3 принимаем ρ=850 кг/м3 v– скорость керосина, м/с ν – кинематический коэффициент вязкости керосина принимаем μ = 2,7·10-6 м2 ·с-1 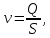 где S – площадь сечения трубопровода 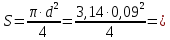 Q = 60 кг/с = 60/ρ = 60/850 = 0,071м3/с d = 90мм = 0,09м 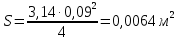 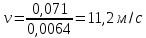 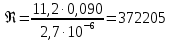 При Re > 10000 – развитое турбулентное течения в трубах Задача 8 Определить местные потери давления на полнопоточном фильтре, установленном в трубопроводе (рисунок 5), если расход жидкости Q, показания манометров p1 = 0,1 МПА, p2 = 0,25 МПА, а диаметры труб d1 = 5 мм, d2 = 10 мм, кинематическая вязкость и плотность жидкости ν = 0,4см2/си плотность ρ =1000 кг/м3. Потерями на трение по длине пренебречь. 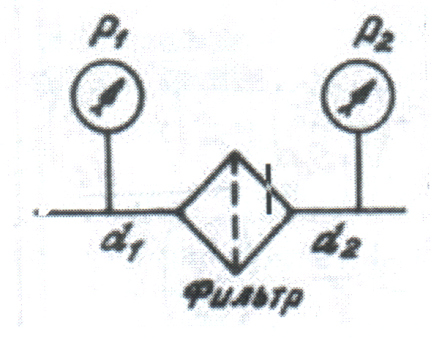 Рисунок 5 Исходные данные: Q = 1,3 л/с; Решение Определяем среднюю скорость в трубопроводах 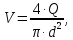 где Q – расход жидкости Q = 1,3 л/с = 1,3 · 10-3 м3/с d – диаметр трубы 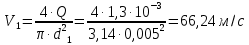 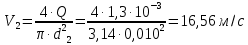 Определяем критерий Рейнольдса 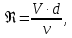 где ν – кинематическая вязкость жидкости, ν = 0,4см2/с = 0,4 · 10-4 м2/с 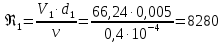 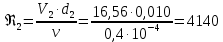 При Re > 2300 режим движения жидкости турбулентный. Составим уравнение Бернулли для установившегося движения жидкости 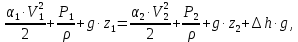 где V1 и V2 − средние скорости соответственно в первом и втором сечениях; P1 и P2 − давления; z1 и z2 – расстояния от произвольной горизонтальной плоскости сравнения до центров сечений, в нашем примере z1 = z2 = 0 1 и 2 = коэффициент неравномерности распределения скорости, при турбулентном режиме движения = 1,0 1,5, принимаем 1 = 2 = 1 Δh – местные потери давления на полнопоточном фильтре, которые определяе из уравнения Бернулли 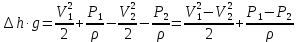 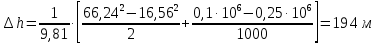 Задача 9 В бак, разделенный на две секции перегородкой (рисунок 6) с отверстием, поступает вода в количестве Q. Из первой секции вода вытекает через цилиндрический насадок, а из второй – через конический насадок, с углом конусности θ = 60. Диаметры отверстий и входные сечения насадок одинаковы и равны d = 20мм, длины насадок. Определить расход через каждый насадок. 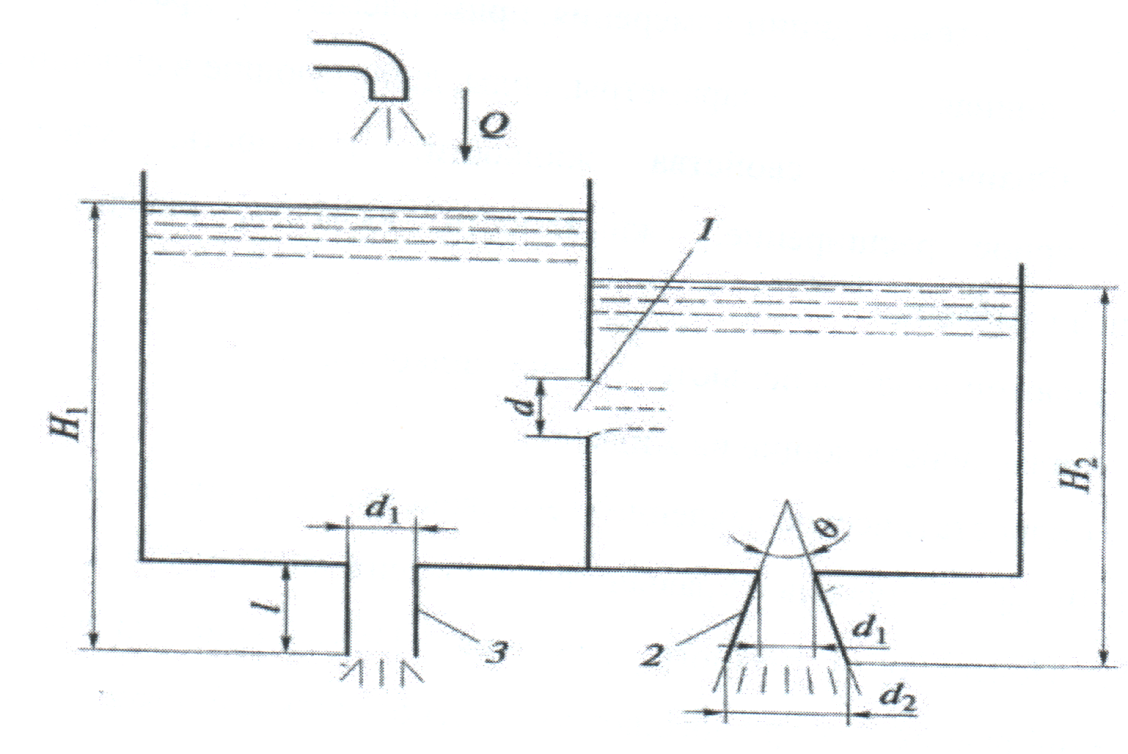 Рисунок 6 Исходные данные: Q = 40 ·10-4 м3/с; l= 55мм Решение При установившемся режиме расход через насадки определяем по формуле: Q = Q1 + Q3, где Q – общий расход воды в бак; Q3 – расход через конический насадок; Q1 – расход через отверстие в перегородке 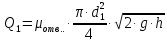 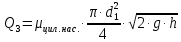 где h = l – длина насадок μцил..нас – коэффициент расхода, отнесенный к выходному сечению, при внешнем цилиндрическом насадке принимаем μцил..нас = 0,82; μотв. – коэффициент расхода, отнесенный к выходному сечению, принимаем μотв. = 0,62; Из рисунка 6 видим, что напор одинаков и получаем 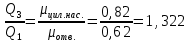 отсюда получаем  и общий расход  Определяем расход через отверстие   Через конический насадок расход равен расходу через отверстие 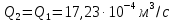 Литература 1. Ухин, Б.В. Гидравлика. Учебное пособие / Б.В. Ухин.- М.: ИД «ФОРУМ»: ИНФРА-М. 2009. 2. Павлов К.Ф., Романков П.Г., Носков А.А. Примеры и задачи по курсу процессов и аппаратов химической технологии. Учебное пособие для вузов. – Альянс, Москва 2006 3. Справочник по гидравлическим расчетам. Под редакцией П.Г.Киселева. «Энергия» Москва, 1972 |
