КР ТЭС. Задача 1 Запишите формулы для расчета спектральных коэффициентов ряда Фурье в комплексной экспоненциальной форме
 Скачать 193.2 Kb. Скачать 193.2 Kb.
|
|
Задача 1 1. Запишите формулы для расчета спектральных коэффициентов ряда Фурье в комплексной экспоненциальной форме. 2. Вычислите спектральные коэффициенты для сигнала, приведенного на рисунке 1. Интервал разложения равен [-τ/2; τ/2]. Число спектральных коэффициентов n = 3. 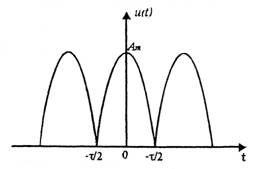 Рисунок 1 – Временная диаграмма сигнала Исходные данные: Длительность импульса τ = 12 мс. Амплитуда импульсов Аm = 3 В. Аналитическое выражение для сигнала на рисунке 1: 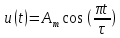 . .Решение: Спектры периодических сигналов являются дискретными. Спектральное разложение можно выполнить также, используя систему базисных функций, состоящую из экспонент с мнимыми показателями: 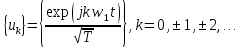 . (1) . (1)Функции этой системы периодичны с периодом Т и ортонормированы на отрезке времени 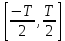 . .Тогда мы получим показательную форму записи ряда Фурье: 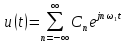 (2) (2)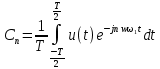 (3) (3)Выражение (2) представляет собой ряд Фурье в комплексной форме. Спектр сигнала в соответствии с формулой (3) содержит компоненты на отрицательной полуоси частот, причём 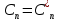 . Слагаемые в ряде (2) с положительными и отрицательными частотами объединяются в пары. . Слагаемые в ряде (2) с положительными и отрицательными частотами объединяются в пары. Отрицательная частота – понятие не физическое, а математическое, вытекающее из способа представления комплексных чисел. Вычислим угловую частоту по формуле: 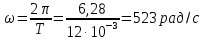 Вычислим спектральные коэффициенты для сигнала, приведенного на рисунке 1 (вычисления проводились в программе Mathcad): 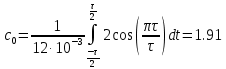 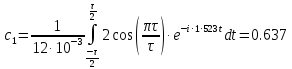 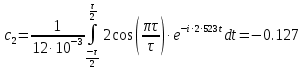 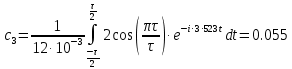 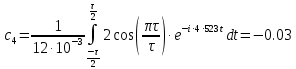 Представим рассчитанные значения в виде таблицы 1. Таблица 1
Задача 2 1. Для сигнала 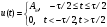 с параметрами с параметрами 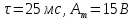 найти спектральную плотность и амплитудный спектр сигнала. найти спектральную плотность и амплитудный спектр сигнала.2. Нарисовать временную диаграмму сигнала (сам сигнал) и амплитудный спектр сигнала. Решение 1. Для разложения в спектр непериодического сигнала используется прямое преобразование Фурье: 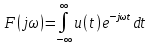 где u(t) – функция, описывающая сигнал. Одним из условий применимости преобразования Фурье к функции u(t) является ее абсолютная интегрируемость: 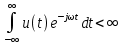 Так как сигнал не является бесконечным, то функция интегрируема абсолютно. Рассмотрим заданный сигнал. Выражение для спектральной плотности запишем: 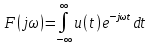 = =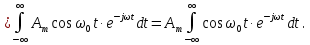 Используя формулу 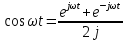 получим: получим: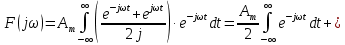 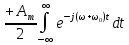 Известно, что: 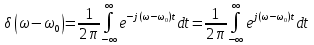 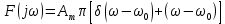 Рассчитаем частоту: 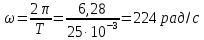 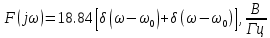 Построим временную и спектральную диаграммы сигнала: Математическая модель заданного сигнала: 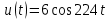 Временная диаграмма представлена на рисунке 2: 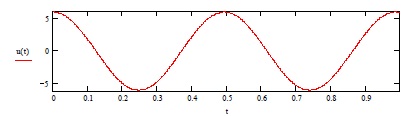 Рисунок 2 – Временная диаграмма заданного сигнала. Спектральная диаграмма представлена на рисунке 3. 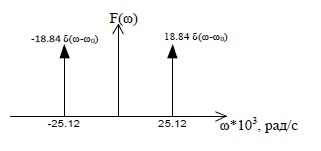 Рисунок 3 – Спектральная диаграмма заданного сигнала. Задача 3 1. Дайте определение автокорреляционной функции (АКФ) сигнала и запишите формулу для ее расчета. 2. Для заданного сигнала U(t) 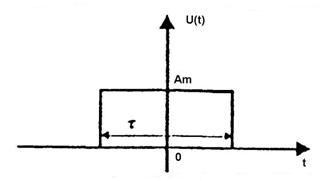 с параметрами τ = 2 мс определите АКФ аналитическим или графическим способом. Амплитуда сигнала Am = 1 В. Решение Автокорреляционная функция – это скалярное произведение сигнала на его сдвинутую копию. Для детерминированного сигнала конечной длительности АКФ определяется следующим выражением: 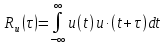 где τ – временной сдвиг сигнала. Для сигналов, являющихся вещественными функциями времени, обозначение комплексного сопряжения можно опустить: 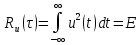 то есть максимальное значение корреляционной функции равно энергии сигнала. Автокорреляционная функция сигнала является четной функцией. Эта функция связана с энергетическим спектром сигнала парой преобразований Фурье. Автокорреляционная функция сигнала с неограниченной энергией связана с преобразованиями Фурье со спектральной плотностью мощности и ее максимальное значение определяется не энергией, а средней мощностью сигнала. Данная функция представляет собой прямоугольный импульс. Запишем аналитическое выражение для заданного сигнала: 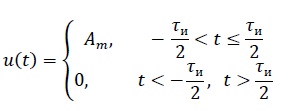 Запишем аналитическое выражение для сдвинутого сигнала: 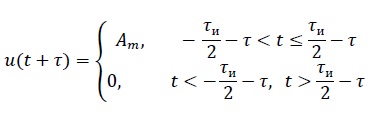 Рассчитаем АКФ: 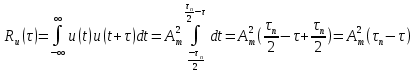 Данное выражение получено для τ > 0. Для сдвига τ < 0 аналогично может быть получено выражение: 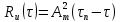 Тогда АКФ заданного сигнала: 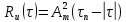 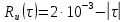 Задача 4 1. Приведите формулу для определения энергии. 2. Определите энергию сигнала 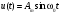 с параметрами: с параметрами: 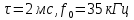 . Амплитуда сигнала Am = 1В. . Амплитуда сигнала Am = 1В.Решение Под энергией сигнала принимают величину: 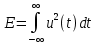 Если сигнал имеет конечную длительность τ, то есть не равен нулю на отрезке времени [-τ/2, τ/2], то его энергия определяется: 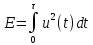 Рассчитаем энергию заданного сигнала: 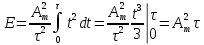 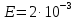 Рассчитаем частоту: 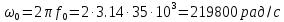 Математическая модель заданного сигнала: 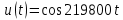 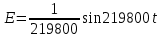 Задача 5 1. Для модулированного сигнала с амплитудной модуляцией с параметрами (таблица 2) записать математическую модель модулированного сигнала, найти спектральную плотность и амплитудный спектр сигнала. 2. Нарисовать временную диаграмму модулированного сигнала (один период модулирующего сигнала) и амплитудный спектр сигнала. Несущее колебание: 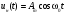 Модулирующий сигнал: 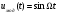 Таблица 2
Решение Несущее колебание: 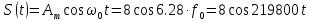 Запишем модулирующий сигнал: 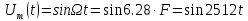 Запишем математическую модель амплитудно-модулированного сигнала: 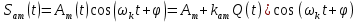 Спектральную плотность определим по формуле: 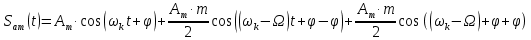 АМ сигнал при модуляции гармоническим сигналом состоит из трех спектральных составляющих с частотами: несущей 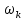 , нижней боковой , нижней боковой 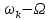 , верхней боковой , верхней боковой 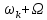 . Спеткральная диаграмма однотонального АМ сигнала симметрична относительно несущей частоты. Амплитуды боковых колебаний одинаковы ( . Спеткральная диаграмма однотонального АМ сигнала симметрична относительно несущей частоты. Амплитуды боковых колебаний одинаковы (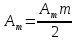 ) и при ) и при 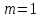 не превышают половины амплитуды несущего колебания. не превышают половины амплитуды несущего колебания.Представим временные и спектральную диаграммы. 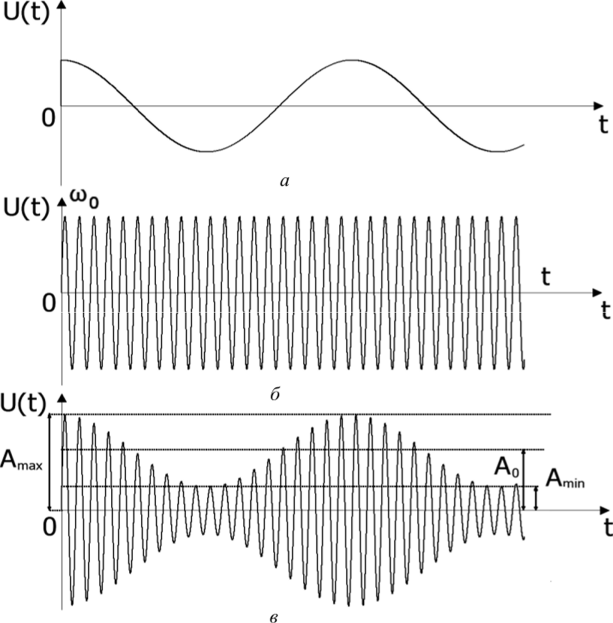 Рисунок 5 – Временные диаграммы модулирующего, несущего и ФМ сигналов. 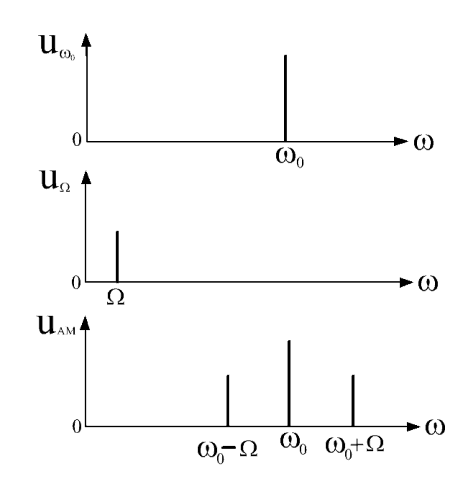 Рисунок 5 – Спектральная диаграмма ФМ сигнала. Задача 6 1. Для сигнала 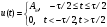 с параметрами τ = 25мс, Am = 15В, вычислить частоту дискретизации fд = fд.мин + 20%, где fд.мин – минимально возможная частоты дискретизации в соответствии с теоремой Котельникова. Вычислить спектральную плотность и амплитудный спектр дискретизированного сигнала. с параметрами τ = 25мс, Am = 15В, вычислить частоту дискретизации fд = fд.мин + 20%, где fд.мин – минимально возможная частоты дискретизации в соответствии с теоремой Котельникова. Вычислить спектральную плотность и амплитудный спектр дискретизированного сигнала. 2. Нарисовать временную диаграмму дискретизированного сигнала и амплитудный спектр сигнала. Решение Теорема Котельникова: всякий непрерывный сигнал U(t) со спектром, ограниченным частотой Fmax, может быть представлен последовательностью своих мгновенных значений (отсчетов), взятых через интервалы времени 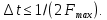 Так как задана синусоида, у нее имеется только одна частота, то частота дискретизации по теореме Котельникова равна: 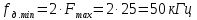 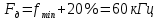 Спектральная плотность гармонического сигнала: 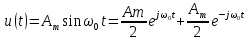 описывается выражением 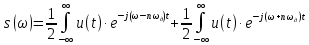 В этом выражении первый интеграл представляет собой спектральную плотность сигнала U(t) на частотах ω-nωд а второй – ту же спектральную плотность, но на частотах ω+nωд. Следовательно, дискретному сигналу соответствует спектральная плотность: 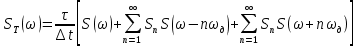 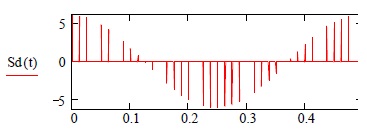 Рисунок 6 – Временная диаграмма дискретизированного сигнала 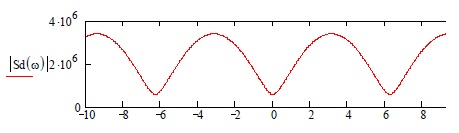 Рисунок 7 – Спектр амплитуд дискретизированного сигнала Список использованных источников 1. Клюев Л.Л. Теория электрической связи. - Мн. : Дизайн ПРО, 1998. 2. Зюко А.Г., Кловский Д.Д., Назаров М.В., Финк Л.М. Теория передачи сигналов. - М. : Радио и связь, 1986. 3. Баскаков С.И. Радиотехнические цели и сигналы. - М. : Высшая школа, 1988. 4. Кловский Д.Д., Шилкин В.А. Теория электрической связи. Сборник задач и упражнений. - М. : Радио и связь, 1990. 5. Баскаков С.И. Радиотехнические цепи и сигналы. Руководство к решению задач. - М. : Высшая школа, 1987. 6. Гоноровский И.С. Радиотехнические цепи и сигналы. - М. : Радио и связь. 1986. 7. Кушнир В.Ф., Ферсман Б.А. Теория нелинейных электрических цепей. - М. : Радио и связь, 1986. 8. Залмакзон Л.А. Преобразования Фурье, Уолша, Хаара и их применение в управлении связью и других областях. - М. : Наука, 1989. 9. Шувалов В.П., Захарченко Н.В. и др. Передача дискретных сообщений. Учебник для ВУЗов / Под. ред. В.П. Шувалова. - М. : Радио и связь, 1990. 10. Биккенин Р.Р. Теория электрической связи: учеб. пособие для студ. высших учебных заведений / Р. Р. Биккенин, М. Н. Чесноков. – М. : Издательский центр «Академия», 2010. – 336с. |

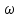 , рад/с
, рад/с